②微波成像技术国家级重点实验室 北京 100190
③中国科学院大学 北京 100190
②Science and Technology on Microwave Imaging Laboratory, Beijing 100190, China
③University of Chinese Academy of Sciences, Beijing 100190, China
合成孔径雷达(Synthetic Aperture Radar,SAR)是一种主动遥感设备,具有全天时全天候和高分辨大区域成像的能力,在军事、民用及其它领域有着广泛应用。常规SAR模式依赖传感器平台的直线飞行轨迹,该成像模式下,一方面存在着由于地形起伏引起的迭掩、透视缩短和阴影等SAR影像固有变形现象;另一方面由于合成孔径积累时间内观测视角受限,仅能获取观测对象在某小范围方向上的后向散射,给SAR图像解译和目标识别带来了特殊的难题。与传统SAR模式不同,圆迹SAR通过平台圆周运动和波束控制实现对目标的全方位360°观测,可以获取目标区域的全方位散射特性,其优势包括3维成像能力、高分辨率、高信噪比等。建筑物信息提取在军事监视、土地使用调查和城市规划等方面有着极为广泛的应用,按照雷达回波信号路径不同,建筑物产生的后向散射主要分为面散射、偶次散射和体散射,其中偶次散射最为明显。CSAR可实现多个不同角度场景的大视角范围连续成像观测,通过多角度观测的互补性以及对回波进行综合,有效利用相干累积角实现大信噪比高分辨率成像,提升建筑物散射信息的获取能力和几何特征提取、抑制阴影能力[1, 2]。
常规SAR模式成像的固有缺陷会造成建筑物SAR图像明显的几何畸变,在不同成像条件下,同一建筑物就有可能表现出很大的形状差异,且其局限于单一观测视角,不能获得目标随方位角变化的多角度散射特性。而现有的CSAR建筑物成像方法中,主要是通过360°全相干累积成像,这会导致建筑物SAR图像的信噪比恶化,散射信息缺失,影响到极化目标分解时对建筑物散射机理的提取[3]。建筑物的散射特征以二面角散射为主,具有较强方向性,由于不再满足各向同性假设条件,传统的全相干处理不仅造成图像散焦、信噪比降低等问题,还将破坏目标的方位散射信息[4]。2013年法国ONERA 利用机载圆迹SAR实验获取的X波段数据,对建筑物和车辆进行优化成像,采用处理的方法是将360°回波数据划分为360个1°大小的子孔径分别成像,之后再对这360个子孔径图像做非相干叠加,较为详细地呈现了建筑物和车辆清晰的轮廓信 息[5]。
本文提出一种相干与非相干处理相结合的圆迹SAR建筑物全方位优化成像方法。首先,由于建筑物的散射特性可近似用二面角反射器来理解,利用电磁仿真软件FEKO建立二面角反射器的电磁散射模型,并采用物理光学算法(PO)计算二面角反射器的雷达散射(RCS);其次,用仿真模拟得到的RCS生成雷达回波数据,进行不同方位相干累积角度CSAR成像,并与散射各向同性情况下的成像指标和信噪比进行分析比较,得出对建筑物CSAR成像最佳方位相干累积角度大小;最后,将CSAR的360°回波数据划分为小角度重叠的多个子孔径并利用BP成像算法分别成像,各像素取子孔径图像中的幅度最大值获得全方位合成图像,以VV通道为基准取得全极化数据并进行Pauli目标分解,获取到建筑物场景的轮廓信息。 2 建筑物散射模型建立与分析
在高分辨率SAR图像中,对于建筑物目标而言,按照雷达回波信号传播路径的不同,建筑物产生的后向散射主要分为面散射、偶次散射和体散射。其中面散射主要来自地面、墙面和屋顶的散射;偶次散射主要是来自于地面-墙体或者墙体-地面的二次弹射;体散射主要指的是电磁波在墙面和地面之间多次反射。实际中很难将具体散射点和建筑物上发生的散射结构进行分析,由于建筑物屋顶面比较平滑,后向散射较弱,而建筑物墙体和地面之间形成的偶次散射最为明显,因此可以通过矩形金属二面角反射器的散射特性来近似解释建筑物的散射特性[6]。
FEKO是3维任意结构全波电磁场分析软件,通过参数设置和模型建立,利用PO算法计算远场模拟回波[7]。针对已有的P波段数据来设置FEKO 模型仿真参数,其中二面角散射模型的尺寸和雷达波长在一个量级上,以便于点目标仿真分析;实际全通道P波段数据中,VV通道散射能量最大,所以模型选用VV极化方式。利用FEKO建立的二面角散射模型如图 1所示。模型参数具体设置如表 1所示,其中λ为雷达波长。

|
图 1 二面角反射器散射模型 Fig.1 The scattering model of dihedral reflector |
| 表 1 二面角反射器模型主要参数 Tab. 1 The main parameters of the dihedral reflector model |
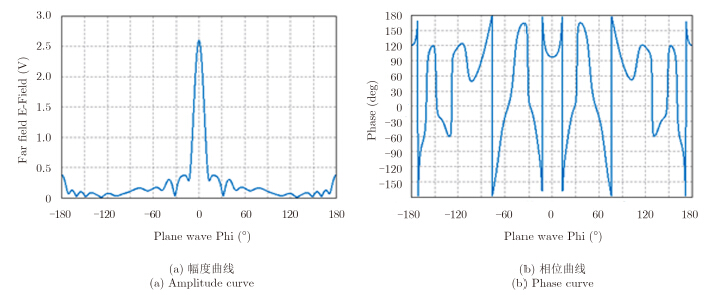
令该模型天线入射角 $\phi = {45^\circ }$ ,方位角$θ=-180°~ 180°$,采用PO算法计算远场二面角反射器的RCS,FEKO仿真得出RCS幅度值和相位值随方位角变化曲线,如图 2所示。
|
图 2 二面角反射器RCS幅度和相位曲线 Fig.2 The RCS amplitude and phase curve of the dihedral reflector |
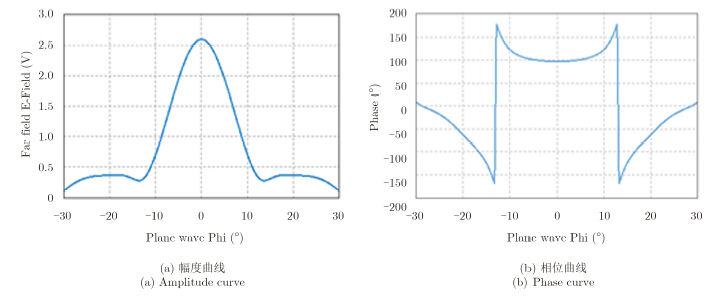
由仿真得出的RCS全方位360°幅度值和相位值可以看出,二面角反射器在方位角为0°时,RCS幅度值最大,相位值约为90°,且相位值在方位角0°左右波动范围比较小。根据全方位的RCS幅度和相位变化曲线,以及相干累积原理可知,该模型下,CSAR最佳方位相干累积角度应当以0°为中心的小范围方位向角。为了更清楚地显示二面角散射在方位向的稳定性,图 3给出了方位角从-30°~30° 的RCS变化范围。
|
图 3 二面角反射器RCS幅度和相位曲线 Fig.3 The small range RCS amplitude and phase curve of the dihedral reflector |
由图 3可知,RCS相位在方位相干累积角度为-13°~13°时平稳变化,之后变化范围较大;RCS 幅度在3 dB宽度时,方位相干累积角度-8°~8°。所以,仅从RCS幅度和相位变化曲线来分析,最佳方位相干累积角度应在16°~26°范围内。以上仅是对FEKO仿真得到的RCS进行分析,对此,文献[8] 和文献[9]利用PO对二面角反射器的RCS进行理论分析。经过比较二面角仿真和理论分析得到的RCS可看出,二者结论基本相同,这也从理论确定了最优方位相干累积角度的选择范围。后文将通过对CSAR成像结果分析,进一步确定最佳方位相干累积角度。 2.2 CSAR成像结果分析
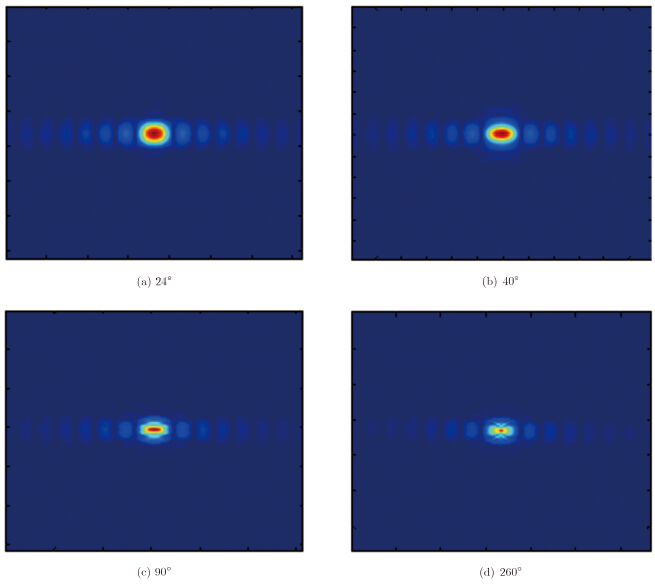
假设天线的入射角为45°,以下分析方法也可用于其它入射角的情况,本节以45°入射角为例,对理想的各向同性点目标和二面角的CSAR成像结果进行比较,得出二面角的最佳方位相干累积角度范围。由FEKO建立的二面角反射器模型仿真计算得出其RCS幅度值和相位值,即可生成相应的二面角CSAR回波数据。CSAR成像时,随着方位角度的增加,方位向分辨率增大并且和距离向耦合度增强。从实际CSAR点目标仿真结果可知,峰值旁瓣比(PSLR)在方位角度增加时,出现主瓣、旁瓣无法辨清和主瓣宽度增大等问题。用FEKO仿真生成的二面角CSAR回波数据,取不同方位相干累积角度范围进行成像,结果如图 4所示,从图中可以看出大角度的方位相干累积会带来散焦问题。
|
图 4 二面角不同方位相干累积角度CSAR成像结果 Fig.4 The CSAR imaging results of different azimuth accumulation of dihedral reflector |
假设回波信号中噪声为高斯白噪声,则CSAR图像信噪比近似等于在方位相干累积角度范围内回波信号能量相干累积与方位向采样数之比,如式(1)所示,其中方位向采样点 $Na = \phi \cdot \Delta \phi $ ,$\Delta \phi $ 为方位角度采样间隔,Si为第i个方位向采样点回波复信号。
| ${\rm{SNR}} = {\frac{{{\rm{ }}\left| {\sum\limits_{i = 1}^{Na} {{S_i}} } \right|}}{{Na}}^2}$ | (1) |
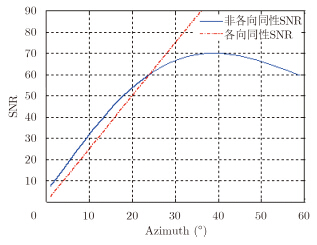
由式(1)结合图 3所示的二面角反射器RCS幅度和相位变化曲线可看出,在非各向同性情况下,随着方位角度的增加,信号能量增加速率会逐渐减小,随之信噪比也会先增后减。而对各向同性理想点目标,其信号能量近似等于非相干累积,信噪比随着方位角直线上升,对理想点目标和二面角的信噪比仿真结果如图 5所示,可知方位角度在25°左右时最接近各向同性情况下的SNR。
|
图 5 不同情况下SNR比较 Fig.5 The relative SNR of different conditions |
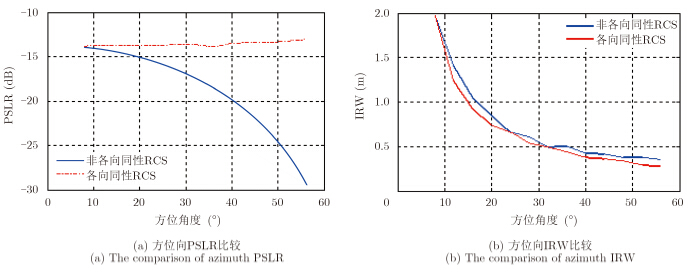
考虑到不同情况下信噪比仿真结果,这里选用10°~60°为方位相干累积角度范围进行散射各向同性情况下点目标和二面角反射器成像结果比较分析,得出二者方位向PSLR,IRW比较曲线图和距离向PSLR,IRW比较曲线图,分别如图 6、图 7 所示。
|
图 6 不同RCS方位向成像结果比较 Fig.6 The comparison of azimuth CSAR imaging results |
|
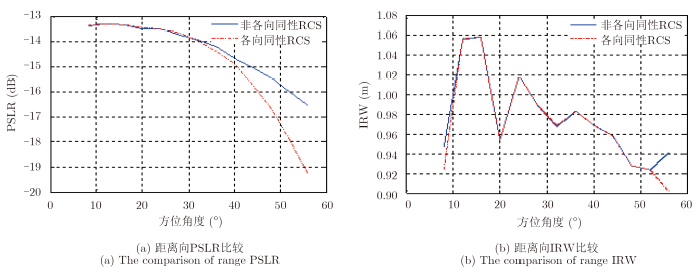
图 7 不同RCS距离向成像结果比较 Fig.7 The comparison of range CSAR imaging results |
由以上比较结果可得出:随着方位相干累积角度的增加,二者方位向PSLR差值越来越大,距离向PSLR值在方位相干累积角小于30°之前几乎相等;方位向IRW值在方位相干累积角为25°和32°时相等,之后IRW值变化缓慢,距离向IRW值近似相等。综合以上分析,方位相干累积角在25°左右时,非各向同性RCS成像结果在保证分辨率和信噪比的同时,最接近散射各向同性情况下理想点目标成像,也即由FEKO建立的二面角反射器模型的最佳方位相干累积角为25°。 3 CSAR优化成像算法
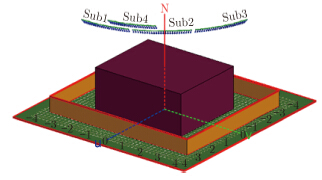
基于上一节建筑物散射模型建立和分析得出的最佳成像方位相干累积角度,以及建筑物的几何特征,本节给出一种相干与非相干处理相结合的CSAR建筑物全方位优化成像方法。实际场景中,目标的散射方向是未知的,若直接对建筑物进行方位相干累积角为25°子孔径成像,且子孔径与子孔径之间无重叠部分,会导致无法完整获得建筑物的全方位散射信息,场景模型示意如图 8所示,其中包含有地面、墙体和建筑物。
|
图 8 建筑物群落散射示意图 Fig.8 Scatter diagram of building community |
示意图中对建筑物照射有4个25°大小的子孔径,Sub1,Sub2,Sub3和Sub4,在传统的CSAR处理方法中有直接非相干融合互不重叠的子孔径Sub1,Sub2和Sub3。显然,尽管这3个子孔径的方位相干累积角度为最佳25°,但是这会使得部分散射信息缺失,例如,若子孔径Sub1,Sub2和Sub3所照射的目标不是类似二面角的散射特性,而子孔径Sub4所照射的目标正好是,如此便会导致无法获得建筑物完整的全方位散射信息。
解决这一问题的方法就是使子孔径与子孔径之间互相重叠,如图 8中子孔径Sub1和Sub4 重叠。子孔径间的重叠角度大小取决于二面角中心与天线中心的对应关系,理想情况下二面角的中心应该正对着最优方位相干累积角度的中心,才能保留二面角的全部散射信息。若子孔径之间偏移角度过大,会使对应的部分二面角散射信息缺失;若子孔径之间偏移角度过小,又会增加计算量。为了得出最优的偏移角度 $\gamma $ ,需要仿真分析最大可能出现丢失二面角信息的偏移角,也即 $\gamma $ /2处。利用FEKO建立模型使得方位角偏离二面角中心 $\gamma $ /2,仿真得出RCS并进行成像分析,结果如表 2所示。
| 表 2 不同偏移角下二面角CSAR仿真结果 Tab. 2 The imaging results of dihedral reflector in different overlapping angles |
由表 2可以看出,当 $\gamma $ =2.5°时,也即偏移角度为5°,重叠角度为20°时,二面角成像分析结果接近理想情况下成像结果,结合考虑计算量,选择重叠的方位相干累积角度为20°。
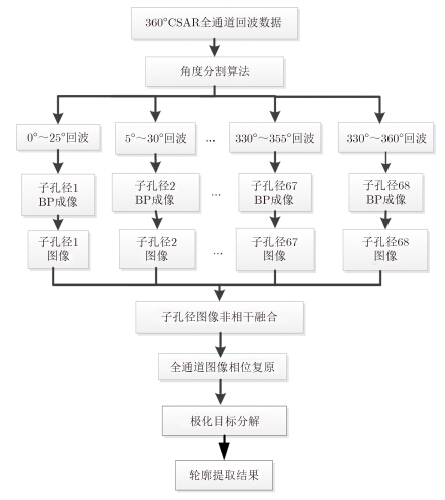
前文论述了子孔径划分与重叠的必要性,在处理建筑物场景的360°回波数据时,对划分好的子孔径进行BP成像,并对得到的所有子孔径SAR图像进行非相干融合,本文选用的非相干融合方法是取子孔径像素最大值,即可得到优化后的建筑物SAR图像。为了验证此优化成像方法的有效性,对得到的全通道SAR图像进行极化目标分解,进一步提取目标散射信息。上述即为相干与非相干处理相结合CSAR优化成像算法,其流程如图 9所示。
|
图 9 CSAR建筑物优化成像算法流程图 Fig.9 The flow chart of CSAR building optimization algorithm |
算法流程图中的角度分割算法主要是将360°CSAR回波数据分割成68个方位相干累积角为25°的子孔径,且子孔径间相互重叠。利用BP成像算法对子孔径重叠后CSAR数据进行成像,并对得到的子孔径图像取各像素幅度最大值获得全方位合成图像[10, 11, 12]。由于已有的的P波段CSAR数据中,VV通道的散射能量最大,所以先获得全极化数据中VV通道的全方位合成图像,按照所合成图像中各像素取值所在的子孔径位置,进而获得HH,HV和VH 3个通道的合成图像,以便于之后的极化目标分解。POLSAR相对于单极化SAR的显著特点是其能够通过获取目标完整的极化散射信息来揭示地物的散射机理。在取得全通道CSAR合成图像后,利用Pauli目标分解,使得更好地解译建筑物轮廓信息[13, 14, 15]。 4 P波段圆迹SAR实验结果与分析
本实验采用的P波段360°全方位圆迹SAR数据是由中国科学院电子学研究所,微波成像技术国家级重点实验室利用自主研制的P波段全极化SAR系统,在四川省绵阳市彰明镇获取的。实验参数如下:全极化、雷达中心频率fc=620 MHz、天线入射角为45°,选取一个建筑物群落场景作为实验目标来处理,建筑物区域实际场景光学图如图 10所示。

|
图 10 建筑物场景的光学影像 Fig.10 The building scenes of optical image |
对实际回波数据按照图 9所示流程进行建筑物CSAR优化成像,为验证本文方法的有效性,这里分别对CSAR全方位360°相干累积成像,子孔径方位相干累积角度分别为10°、25°、50°进行CSAR优化成像,其中三者的子孔径重叠角度分别为5°、20°和45°,成像结果如图 11、图 12所示。

|
图 11 建筑物场景在不同方法、不同子孔径下CSAR成像结果 Fig.11 The CSAR imaging results of buildings under different methods and sub aperture |

|
图 12 建筑物场景在不同方法下CSAR极化目标分解结果 Fig.12 The polar decomposition results of buildings under different methods and coherent accumulation |
图 11中展示了目标建筑物在未作极化目标分解时,全方位360°相干累积成像结果和不同子孔径方位相干累积角度下CSAR优化成像结果。由图 11(a)和图 11(c)相比较可看出,360°相干累积CSAR成像信噪比恶化,而子孔径方位相干累积角度为25°的CSAR优化成像方法信噪比极佳,成像效果好;由图 11(b)、图 11(c)和图 11(d)相比较可以看出,子孔径方位相干累积角度为25°的CSAR优化成像方法成像质量远高于子孔径方位相干累积角为10°和50°的,由此也验证了前文对建筑物散射模型建立和分析的正确性。
图 12展示了全方位360°相干累积、子孔径25°方位相干累积的Pauli目标分解RGB图。其中,红色代表二次散射,即HH-VV;绿色代表体散射,即2HV;蓝色代表单散射,即HH+VV[16, 17]。通过对比观测图 12(a)与图 12(b),可以看出子孔径25°相干累积的极化目标分解结果质量较好。一方面,可看出图 12(b)中场景轮廓比较清晰,如场景区农田部分S1,显然图 12(b)的轮廓更为清晰;最具明显的是场景区电线部分S2,在图 12(a)中几乎看不到电线,而图 12(b)可以清楚地看到电线位置和数目。另一方面,通过极化目标分解RGB图可以看出分解后地表区域呈现较强的体散射,主要原因是360°相干累积成像使得HV通道能量值偏高,这与实际情况不相符,粗糙地表会呈现出一定的极化分量,然而对P波段来说,仍满足小尺度模型,所以地表应有较强的面散射,在图 12(b)中可看出地形区域中体散射不再像图 12(a)中那样占地导地位,其与面散射共存,这才与实际情况相符。
从图 11和图 12的建筑物CSAR成像分析结果可以得出,相对于传统的CSAR成像方法,本文提出的相干与非相干处理相结合的CSAR优化成像算法使场景中建筑物的成像质量有了显著提高,场景周围具有二面角特性的田埂树干等成像结果也更为清晰[18]。 5 结束语
本文结合建筑物固有的散射特性和几何特点,利用FEKO建立了二面角反射器散射模型并进行多个角度分析,得出对建筑物CSAR成像最佳方位相干累积角度大小,进而提出一种相干与非相干处理相结合的CSAR优化成像方法。P波段机载圆迹SAR数据处理结果表明该成像方法优于传统全相干累积方法。本文研究是以P波段、45°入射角为例的,这一分析方法也可用于其它波段和入射角。
| [1] | 洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135. Hong Wen. Progress in Circular SAR imaging technique, Journal of Radars, 2012, 1(2): 124-135.(  1) 1) |
| [2] | 林赟. 圆迹合成孔径雷达成像算法研究[D]. [博士论文], 中国科学院电子学研究所, 2011: 15-21. Lin Yun. Study on algorithms for circular synthetic aperture radar imaging[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2011: 15-21.(  1) 1) |
| [3] | 林赟, 谭维贤, 洪文, 等. 圆迹SAR极坐标格式算法研究[J]. 电子与信息学报, 2010, 32(12): 2802-2807. Lin Yun, Tan Wei-xian, Hong Wen, et al.. Polar format algorithm for circular synthetic aperture radar[J]. Journal of Electronics & Information Technology, 2010, 32(12): 2802-2807.(  1) 1) |
| [4] | 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2005: 22-38. Huang Pei-kang, Yin Hong-cheng, and Xu Xiao-jian. Radar Target Feature[M]. Beijing: Publishing House of Electronics Industry, 2005: 22-38.( 1) 1) |
| [5] | Dupuis X and Martineau P. Very high resolution circular SAR imaging at X band[C]. IGARSS, 2014: 930-933.( 1) 1) |
| [6] | 赵凌君. 高分辨率SAR图像建筑物提取方法研究[D]. [博士论文], 国防科技大学, 2009: 20-25. Zhao Ling-jun. Study on extraction method of high resolution SAR image building [D]. [Ph.D. dissertation], National University of Defense Technology, 2009: 20-25.(  1) 1) |
| [7] | 范丽思, 崔耀中. FEKO 5.4实例教程[M]. 北京: 国防工业出版社, 2012: 1-19. Fan Li-si and Cui Yao-zhong. FEKO 5.4 Instance Tutorial[M]. Beijing: National Defence Industry Press, 2012: 1-19.( 1) 1) |
| [8] | 范菊红, 王月清. 二面角反射器的RCS特性分析[J]. 舰船电子工程, 2006, 26(2): 148-151. Fan Ju-hong and Wang Yue-qing. Analysis of RCS characteristic of dihedral corner[J]. Ship Electronic Engineering, 2006, 26(2): 148-151.(  1) 1) |
| [9] | 周力行. 二面角反射器的RCS预估[J]. 长沙电力学院学报, 1997, 12(3): 276-279. Zhou Li-xing. RCS estimation of the dihedral reflector[J]. Journal of Changsha University of Electric Power, 1997, 12(3): 276-279.(  1) 1) |
| [10] | Oriot H and Cantalloube H. Circular SAR imagery for urban remote sensing[C]. Proceedings of the European Conference on Synthetic Aperture Radar, Friedrichshafen, 2008, 2: 205-208.( 1) 1) |
| [11] | Guo Zheng-yu, Lin Yun, Tan Wei-xian, et al.. Circular SAR motion compensation using trilateration and phase correction[C]. Proceedings of the IET International Radar Conference, Xi'an, China, 2013: 1-5.( 1) 1) |
| [12] | Antje T, Erich C, Karsten S, et al.. Building recognition from multi-aspect high-resolution InSAR data in urban areas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3583-3593.( 1) 1) |
| [13] | Soumekh M. Reconnaissance with slant plane Circular SAR imaging[J]. IEEE Transactions on Image Processing, 1996, 5(8): 1252-1265.( 1) 1) |
| [14] | 孙萍. 极化SAR图像建筑物提取方法研究[D]. [硕士论文], 首都师范大学, 2013: 3-9. Sun Ping. Research on extraction method of polarization SAR building image[D]. [Master dissertation], Capital Normal University, 2013: 3-9.(  1) 1) |
| [15] | Ponce O, Prats-Iraola P, Pinheiro M, et al.. Fully polarimetric high-resolution 3-D imaging with Circular SAR at L-Band[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3074-3090.( 1) 1) |
| [16] | Ponce O, Prats P, Scheiber R, et al.. Analysis and optimization of multi-circular SAR for fully polarimetric holographic tomography over forested areas[C]. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Melbourne, Australia, 2013: 2365-2368.( 1) 1) |
| [17] | Ponce O, Prats-Iraola P, Scheiber R, et al.. Polarimetric 3-D reconstruction from multicircular SAR at P-band[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(4): 803-807.( 1) 1) |
| [18] | 刘燕, 谭维贤, 林赟, 等. 基于圆迹SAR的建筑物轮廓信息提取[J]. 电子与信息学报, 2015, 37(4): 946-952. Liu Yan, Tan Wei-xian, Lin Yun, et al.. Approach of the outlines extraction of building footprints from the Circular SAR data[J]. Journal of Electronics & Information Technology, 2015, 37(4): 946-952.(  1) 1) |
 2015, Vol. 4
2015, Vol. 4
