近几年稀疏表示理论^[1]发展迅速，得到很多学者的广泛关注并被应用到多个领域，如图像编码^{[2, 3]}、图像去噪^{[4, 5]}、人脸识别^{[6, 7]}、SAR图像目标识别^{[8, 9, 10, 11]}等。在SAR图像目标识别方面，文献^[8]提出了一种基于主元分析和稀疏表示的SAR图像目标识别算法，该方法首先对样本进行PCA降维，将降维后的样本进行稀疏表示，利用优化算法求得样本的稀疏系数并作为样本特征，最后利用最近邻法对SAR图像目标分类识别，实验结果表明在没有预处理的情况下该算法能有效地识别目标。

最近有学者将稀疏表示理论运用到特征提取中，如QIAO^[12]等人提出了稀疏保持投影(Sparsity Preserving Projections,SPP)特征提取方法，该方法可保证在投影空间内的样本与稀疏重构样本误差最小，将该特征提取方法运用到人脸识别中，实验结果证明了该方法的有效性。

本文在SPP方法的基础上借鉴局部保持投影(Locality Preserving Projection,LPP)特征提取方法思想^[13]，使得提取的特征在保持稀疏重构误差最小的同时使同类样本间距最小，利用该思想构造目标函数，求解特征空间，在特征空间内利用SVM分类器进行分类，采用MSTAR数据对该方法进行验证，实验结果表明，在不利用目标成像方位信息情况下该方法可以有效地提高目标的正确识别率。

目标的稀疏系数可描述目标的特征，SPP特征提取方法将每个样本的稀疏系数构成稀疏重构权重矩阵，通过寻找最佳投影向量w，使得原始样本在w上的投影与稀疏重构样本在w上的投影误差最小。

设有样本集$X = \{ {x_{_1}},{x_{_1}},...,{x_N}\} $，其中${x_i} \in {R^{M \times 1}}$,N表示样本总数，i=1,2,$ \cdots $,N。对于每一个样本x_i，都存在一个对应的子集${T_i} = \{ {x_1},\cdots ,{x_{i - 1}},{x_{i + 1}},\cdots ,{x_N}\} \in {R^{M \times (N - 1)}}$，通过以下1-范数最小化问题求得每个样本x_i的稀疏系数${\alpha _i}$：

式(1)中稀疏系数可以通过以下1-范数优化方法来求解：

式(2)求解稀疏系数的问题又可转化为有约束的2次规划问题，可以利用梯度投影法^[14]来求解，其优化函数形式如下：

通过式(3)求得每个样本x_i在其对应子集T_i上的稀疏系数${\alpha _i}$后，构造稀疏重构权重矩阵$S = {[{s_1},{s_2},\cdots ,{s_N}]^{\rm{T}}} \in {R^{N \times N}}$，其中，${s_i} = [{\alpha _i},1,{\left. { \cdots ,{\alpha _{i,i - 1}},0,{\alpha _{i,i}},\cdots ,{\alpha _{i,N - 1}}} \right]^{\rm{T}}} \in {R^{N \times 1}}$。由于稀疏表示得到的稀疏系数可描述不同目标的特征，因此希望这种特性在低维空间得到保持，故可通过求得投影向量w，使得样本x_i在w上的投影与稀疏重构样本在w上的投影误差最小，具体目标函数形式如下：

将式(4)整理写成以下形式：

为避免退化解，令${w^{\rm{T}}}X{X^{\rm{T}}}w = 1$，式(5)可以转化成以下优化问题：

式(6)最终转换成求解以下最优化问题：

通过以下特征值分解问题求得投影向量w：

由于SPP特征提取方法是一种全局降维方法，它通过数据的稀疏重构关系求得投影向量，这种稀疏性自然地捕获了数据的局部结构特性。SAR目标图像对成像方位很敏感，不同方位下的SAR图像相差很大，由稀疏表示得到的稀疏系数不能完全满足在同类样本位置上的系数值非零，在其余类样本上的系数值为零，此时利用每类样本稀疏系数构成稀疏重构权重矩阵并不能很好地体现出数据的局部结构关系。本文在SPP方法基础上，对目标函数建立准则进行了改进，即在特征空间内保持稀疏重构误差最小的同时使同类样本间距最小。

改进的SPP特征提取方法目标函数的建立从两个方面考虑：

(1) 保持SPP特征提取的目标函数，即

将式(10)的目标函数转化成以下形式：

(2) 在投影空间建立目标函数使同类样本间距最小，设${y_i} = {u^{\rm{T}}}{x_i},{y_j} = {u^{\rm{T}}}{x_j}$为不同训练样本在投影空间的投影，$i,j = 1,2,\cdots ,N\left( {i \ne j} \right)$，则目标函数的建立如下：

通过运算将式(12)化成以下形式：

结合式(11)和式(13)，可得到改进的稀疏保持投影特征提取方法的目标函数：

该目标函数表示提取的特征在投影空间不仅能保持样本间的稀疏重构误差最小，还保证了同类样本间距最小。

式(14)的求解等价于求以下特征值分解问题：

将式(15)求得的特征值按照从大到小的顺序排列，对应的特征向量为${u_1},{u_2},\cdots ,{u_N}$，取前l个特征值对应的特征向量构成投影矩阵$U = [{u_1},{u_2},\cdots ,{u_l}]$。此时样本${x_i}(i = 1,2,\cdots ,N)$在U上的投影：

采用本文特征提取方法进行SAR图像目标识别框图如图 1所示，下面对算法的各个步骤进行详细介绍。

图 1(Fig. 1)

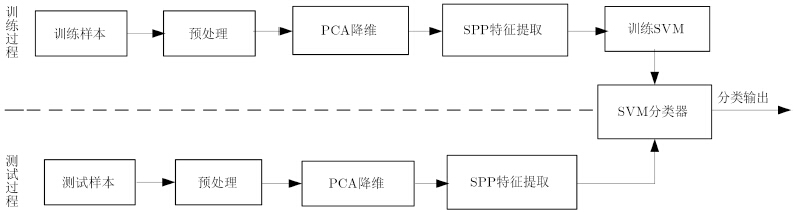图 1 SAR目标识别框图 Fig. 1 A diagram of the SAR target recognition

步骤1 预处理：

(a) 对训练样本集进行对数变换，将乘性噪声转化为加性噪声；

(b) 将对数变换后的样本集进行傅里叶变换，取其幅频特性，以保证目标在图像中的平移不变性，同时利用幅频特性的对称性取一半信息以此来降低样本的维数；

(c) 对幅频特性进行归一化处理，得到预处理后的训练样本。

步骤2 特征提取：由步骤(1)预处理后的图像形成列矢量，并进行PCA处理，以保证当训练样本个数相对于样本维数较小时，式(15)中的XLX^T不可逆^[12]，然后通过式(16)即可得到训练样本集的特征$A = [{q_1}({x_1}),{q_2}({x_2}),\cdots ,{q_N}({x_N})]$。

步骤3 分类：将训练样本集的特征A送到SVM分类器^[15]中进行训练，得到已训练的分类器。

待识别样本采用与训练过程相同的预处理和特征提取方法提取样本特征，并送入已训练好的SVM分类器进行分类，得到测试样本的类别。

本实验所用数据是由美国DARPA/AFRL MSTAR工作组提供的实测SAR地面静止目标数据。该数据包括3大类目标，共7种型号SAR图像，训练样本是在俯仰角为17°时的成像数据，包括T72_132,BMP2_c21,BTR70_c71 3类目标，测试样本是在俯仰角为15°时的成像数据，包括T72的3种型号(T72_132,T72_812,T72_s7)、BMP2的3种型号(BMP2_c21,BMP2_9563,BMP2_9566)和BTR70_c71共7种型号目标。图像大小均为128×128，成像方位为0°～360°。图 2给出了3种训练样本的光学图像，图 3给出了3种训练样本在某一方位角下的SAR图像，图 4给出了T72_132在不同方位下的图像，表 1给出了样本具体类别型号及样本数。

图 2(Fig. 2)

图 2 3类军用目标的光学图像 Fig. 2 The optical image of three military targets

图 3(Fig. 3)

图 3 3类军用目标的SAR图像 Fig. 3 The SAR image of three military targets

图 4(Fig. 4)

图 4 T72_132在3个不同方位角下的SAR图像 Fig. 4 T72_132 under three different azimuth of SAR images

表 1(Tab. 1)

表 1 3类目标训练样本和测试样本 Tab. 1 The training and testing samples in experiments 数据类型 目标类别 与型号样本个数 样本总数 T72_132 232 训练样本 BMP2_c21 233 698 BTR70_c71 233 T72_132 196 T72_812 195 T72_s7 191 测试样本 BMP2_c21 196 1365 BMP2_c9563 195 BMP2_c9566 195 BTR70_c71 196

表 1 3类目标训练样本和测试样本 Tab. 1 The training and testing samples in experiments

实验中，为了提高运算速度，将每幅图像截取图像子块(65×65)，待识别样本经过PCA降维后得到样本维数为233,SVM分类器中核函数选取高斯径向基核函数，$K({x_i},x) = \exp ( - \gamma * ||{x_i} - x|{|^2})$，核参数γ=44。

表 2给出了特征维数l=100时本文方法的识别结果，由表 2可知，本文方法对T72_132,T72_s7,BMP2_c21以及BTR70_c71 4种型号目标都有很好的识别结果，识别率都达到了100%，此外，对其他型号的目标识别率都在90%以上，平均识别率为97.81%。

表 2(Tab. 2)

表 2 各类目标的识别率 Tab. 2 The recognition rate of different samples T72_132 BMP2_c21 BTR70_c71 识别率(%) 平均识别率(%) T72_132 196 0 0 100 T72_812 189 5 1 96.92 T72_s7 191 0 0 100 BMP2_c21 0 196 0 100 97.81 BMP2_c9563 4 186 5 95.38 BMP2_c9566 6 181 9 92.35 BTR70_c71 0 0 196 100

表 2 各类目标的识别率 Tab. 2 The recognition rate of different samples

图 5给出了T72,BMP和BTR 3类目标的稀疏系数分布图，其中每类目标取前50个样本，x轴表示稀疏重构权重矩阵的行，y轴表示稀疏重构权重矩阵的列，z轴表示稀疏重构权重矩阵的值，y轴序号为1～50对应样本分布在T72目标所在的区域，y轴序号为51～100对应样本分布在BMP目标所在的区域，y轴序号为101～150对应样本分布在BTR目标所在的区域。由图 5(a)可知，T72样本稀疏系数非零值主要分布在y轴序号为1～50的区域，即T72目标所在的区域，且在该区域的系数值很大，在其他区域的系数值很小或者为零，由图 5(b)可知，BMP样本稀疏系数非零值主要分布在y轴序号为51～100的区域，即BMP目标所在的区域，且在该区域的系数值很大，在其他区域的系数值很小或者为零，由图 5(c)可知，BTR样本稀疏系数非零值主要分布在y轴序号为101～150的区域，即BTR目标所在的区域，且在该区域的系数值很大，在其他区域的系数值很小或者为零。由此表明样本非零大系数值主要分布在每类样本所在的区域，所得的稀疏系数可描述目标的特征。

图 5(Fig. 5)

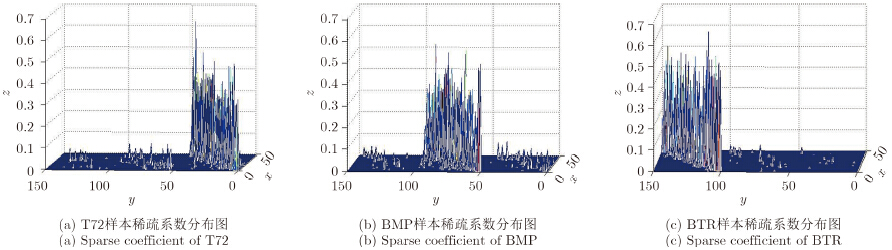图 5 3类样本稀疏系数分布图 Fig. 5 Sparse coefficient distribution of three types of samples

图 6给出了本文方法在不同l取值下的识别结果。由图 6可知，特征维数l的不同会直接影响识别结果，随着特征维数的增加，平均识别率总体呈现增长的趋势。但是对于BMP2_9563和BMP2_9566来说，其识别率随着特征维数的变化波动比较大，这是因为这两类目标是变体且其SAR图像质量明显劣于其它类目标。

图 6(Fig. 6)

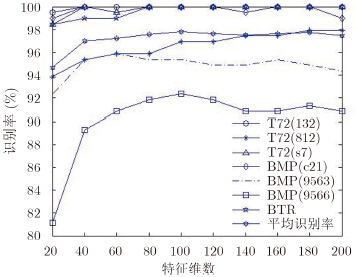图 6 不同特征维数下本文方法的识别结果 Fig. 6 The recognition results of this method under different characteristic dimension

另外，将本文方法与SPP方法进行比较，实验结果如表 3所示，其中SPP方法与本文方法的处理过程相同，且都利用SVM分类器分类识别，T72的识别结果表示T72 3种型号目标的平均识别率，BMP的识别结果表示BMP 3种型号目标的平均识别率。由表 3可知，本文方法在T72和BMP两类目标识别结果上都优于SPP特征提取方法，且平均识别率为97.81%，优于SPP方法。

表 3(Tab. 3)

表 3 不同特征提取方法的识别结果比较 Tab. 3 The recognition results of different feature extraction T72(%) BMP(%) BTR(%) 平均识别率(%) SPP方法 97.77 94.55 100 96.71 本文方法 98.97 95.91 100 97.81

表 3 不同特征提取方法的识别结果比较 Tab. 3 The recognition results of different feature extraction

图 7还给出了两种方法在不同特征维数l下的识别结果比较。由图 7可知，本文方法明显优于SPP特征提取方法，当特征维数为40时，本文方法识别结果已达到97%，说明当特征维数较低时，本文方法仍能取得较好的识别结果。

图 7(Fig. 7)

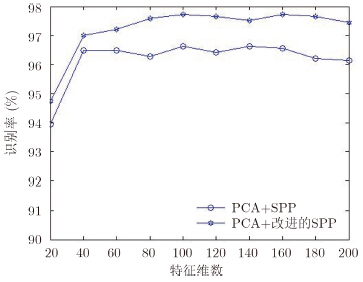图 7 两种方法不同特征维数下的识别结果比较 Fig. 7 Two methods of comparing the identification results under different characteristic demension

本文是在SPP特征提取方法的基础上进行改进的，SPP特征提取方法根据稀疏重构误差最小得到样本的特征向量，而本文方法以保证稀疏重构误差最小的同时保证同类样本类内距最小为目标函数，确定投影空间提取特征向量，最后利用SVM分类器进行分类识别。实验结果表明该方法在方位角未知的情况下能有效提高目标的正确识别率，是一种有效的识别方法。