Research on scattering models for randomly rough surfaces is an important part of microwave remote sensing theory. Several theoretical scattering models for bare soil surfaces have been proposed over the past decades[1,2,3]. However,the scattering from a randomly rough surface is a very complex problem that does not have a closed-formed solution from the Maxwell equations. Therefore,some approximate analytic solutions can only be used when the geometric scales of the surface are restricted within the valid ranges. Three representative approximate models have been developed,namely,the Kirchhoff Model (KM)[4],the Small Perturbation Model (SPM)[5],and the Integral Equations Model (IEM)[6]. In the broad sense,KM is most suitable for relatively rough surfaces (large-scale roughness surface); however,it is only valid when the electromagnetic wavelength is much smaller than the rough surface curvature radius. Here,the root mean square height (s) and the associated correlation length (l),which define the surface roughness statistically,are both larger than the wavelength. SPM requires a relatively smooth surface (small-scale roughness surface) and is only effective when both s and l are smaller than the electromagnetic wavelength. However,natural surfaces contain various proportions of roughness and may not satisfy the validity conditions of KM or SPM. To improve the applicability of the scattering models,Fung[6] proposed IEM and demonstrated its favorable accuracy. As its basic theory,IEM divides the surface scattering field into two parts: the first part keeps the Kirchhoff field (the near field of tangent plane) as the initial solution,and the other part introduces the compensation field that is used to correct the Kirchhoff field. IEM extends the valid range of the theoretical scattering model and fills the gap between KM and SPM. Therefore,IEM has become the most popular method for calculating the electromagnetic scattering of natural surfaces. Wu[7, 8] introduced two important modifications on IEM that improved the accuracy of the model in simulating randomly rough surfaces. This upgraded version is called Advanced Integral Equations Model (AIEM).
Natural surfaces may comprise complex mixtures of large- and small-scale roughnesses,such as an ocean surface (on which small waves cover the large waves) or some blocks of clod with small granular soil. The electromagnetic scattering properties of this two-scale rough surface can be described by calculating the scattering effect of both sizes of roughness. Ulaby,et al.[9] attempted to solve such problem by introducing a Two-Scale Model (TSM). In this model,the randomly rough surface is assumed to be a combination of a slowly undulating surface,which satisfies the KM condition,and a small perturbation surface for which SPM is valid. When the incident angle is near normal (0°<qi<25°),the scattering is dominated by the large-scale surface roughness. In contrast,at large incident angles (qi>25°),the scattering is dominated by small-scale surface roughness,which is tilted by the slope of the large-scale surface roughness. SPM accounts for the tilting effect by introducing a local coordinate system; the scattering coefficient is then calculated by considering both the large- and small-scale roughnesses. Brown proposed another TSM[10],which is a kind of Fourier function. This model is used for transforming the surface height into a spectrum domain for a perfectly Gaussian surface,which is filtered in its height spectral domain by a low pass filter. The small-scale roughness,represented by the high-frequency spectral region and a first-order perturbation solution of Burrow’s model[11],adequately describes the scattering properties of the surface. Meanwhile,the large-scale roughness,represented by the low-frequency spectral region,is assumed to be sufficiently smooth to form the unperturbed surface and to propose physical optics approaches for determining the scattering field. The final result is the sum of the contributions of both types of scale surface roughness.
These two-scale models,which are often used in ocean surfaces and ocean-like grounds,have been shown to yield excellent results[12]. However,these models have their respective shortcomings. Although Ulaby’s TSM is simple,it cannot easily measure the large- and small-scale roughnesses in the field measurements. Brown’s TSM does not need to measure the two roughness sizes. Moreover,his model adopts a low pass filter with a rectangle window function as its spectral response; however,the rectangle-window filter is not suitable and its validity is related to the spectral shape of the surface,thereby presenting a constraint.
Therefore,a Modified Two-Scale Model (MTSM) is introduced in the current paper. This model presents two essential improvements. First,the randomly rough surface is analyzed in the spectrum domain,whereas the wavelet packet transform,which can freely choose wavelet packet bases and is more flexible than the Fourier transform,is introduced to split the surface height spectral and to calculate the two scale roughness. Second,we derive the formula of MTSM,in which KM is used to simulate the scattering of the large-scale roughness,while the first-order SPM is applied to calculate the small-scale roughness. The total scattering is the sum of the Kirchhoff and first-order SPM scattering.
This paper is arranged as follows: Section 2 discusses the method of splitting the spectral by using the wavelet packet,Section 3 derives the formula of the total scattering,Section 4 presents the validation results,and Section 5 concludes the paper.
2 Surface Roughness Decomposition by Wavelet Packet 2.1 Surface descriptionThe randomly rough surface is assumed to be a Gaussian stationary stochastic process. For any point (x,y) on the surface,the surface height (z(x,y)) is a statistical variable with the following statistical characteristics:
| $\quad\quad E\langle z(x,y)\rangle = 0$ | (1) |
| $\quad\quad E\langle {z^2}(x,y)\rangle = {s^2}$ | (2) |
| \[\quad \quad p(z(x,y)) = \frac{1}{{\sqrt {2\pi } s}}\exp \left\{ { - \frac{{z{{(x,y)}^2}}}{{2{s^2}}}} \right\}\] | (3) |
where E<> is the ensemble average,s is the RMS of surface height,p(z(x,y)) is the probability distribution function,and z(x,y) follows the Gaussian distribution.
According to composite surface scattering[13] and stochastic process theories[14, 15],a Gaussian stationary stochastic process can be decomposed into two independent Gaussian stationary stochastic processes. Therefore,the surface height z(x,y) may be rearranged (Fig. 1) as
| $z(x,y) = {z_k}(x,y) + {z_s}(x,y)$ | (4) |

|
Fig.1 Decomposition of the two-scale roughness surface |
where zk(x,y) is the height of large-scale roughness at (x,y),and zs(x,y) is the height of small-scale roughness.
Given that zk(x,y) and zs(x,y) are independent,the two-scale surface height spectrum S(kx,ky) may be expressed as
| $S({k_x},{k_y}) = {S_s}({k_x},{k_y}) + {S_k}({k_x},{k_y})$ | (5) |
where Sk(kx,ky) and Ss(kx,ky) are the height spectra for zk(x,y) and zs(x,y). In addition,kx and ky are the wave numbers of the electromagnetic field incident upon the rough surface along the x and y directions,respectively.
Eqs. (4) and (5),along with the fact that zk(x,y) and zs(x,y) are zero-mean Gaussian,are crucial to the development of the model. If z(x,y) is non-Gaussian,the densities of zk(x,y) and zs(x,y) and their derivatives cannot be uniquely defined[16]. More importantly,the spectral dichotomy,as expressed by Eq. (5),may be invalid.
The solid line represents the surface of z(x,y),and the dotted line S0 represents the large-scale surface [zk(x,y)] in the x-z plane.
2.2 Surface roughness decomposition by wavelet packetsWavelet is a time-frequency representation that has been used successfully in a broad range of applications,particularly in signal analysis[17, 18]. Wavelet packets resulted from the development of wavelet Multi-Resolution Analysis (MRA),a generalization of the wavelet transform that allows for arbitrary tree-shape bandpass filtering,and can be adapted to the characteristics of the particular signal that is being analyzed.
Details of the wavelet transform can be found in several studies[17, 19, 20]. In wavelet MRA,the Hilbert space [L2(R)] is separated to the orthogonal sum of all subspaces given by
| ${L^2}(R) = \oplus {W_j} \,,\,\,j \in Z$ | (6) |
where $W_j$ represents the subspaces of the wavelet basis function j(t). To develop the frequency resolution,we further divide the wavelet subspace Wj according to the binary frequency segment. Therefore,the wavelet scaling subspaces Vj and Wj can be jointed and represented by a new space ${U_j}^n\left( {n \in N} \right)$. If we suppose Uj0 = Vj and Uj1 = Wj,as the orthogonal decomposition formula of L2(R),${V_{j + 1}} = {V_j} \oplus {W_j}$ can be written as the decomposition of Ujn,which is expressed as
| $U_{j + 1}^0 = U_j^0 \oplus U_j^1$ | (7) |
In Eq. (7),Ujn and Uj2n are defined as the wavelet subspaces of un(t) and u2n(t),respectively,and un(t) must satisfy the equations given by
| $\quad\quad{u_{2n}}(t) = \sqrt 2 \sum\limits_{k \in Z} {g(k){u_n}(2t - k)} $ | (8) |
| $\quad\quad{u_{2n + 1}}(t) = \sqrt 2 \sum\limits_{k \in Z} {h(k){u_n}(2t - k)} $ | (9) |
where g(k) and h(k) are the lowpass and highpass filter coefficient,respectively,and are related by
| $h(k) = {( - 1)^k}g(1 - k)$ | (10) |
When n=0,Eqs. (8) and (9) can be rewritten as
| ${u_0}(t) = \sqrt 2 \sum\limits_{k \in Z} {g(k){u_0}(2t - k)} $ | (11) |
| ${u_1}(t) = \sqrt 2 \sum\limits_{k \in Z} {h(k){u_0}(2t - k)} $ | (12) |
The scaling function j(t) and basis function f(t) in wavelet MRA are respectively presented as
| $\varphi (t) = \sqrt 2 \sum\limits_{k \in Z} {g(k)} \varphi (2t - k)$ | (13) |
| $\phi (t) = \sqrt 2 \sum\limits_{k \in Z} {h(k)} \varphi (2t - k)$ | (14) |
By comparing Eqs. (11)–(14),we find that u0(t) and u1(t) are degenerated into j(t) and f(t),respectively. In addition,{un(t)} is the orthogonal wavelet packet that is determined by u0(t) =
f(t). Therefore,the wavelet decomposition is the special column of the wavelet packet. When n=0,we use u0(t) and u1(t) as the subspaces of the wavelet packet,and the wavelet packet transform changes into the wavelet transform. However,if we continue decomposing the high-frequency spectral by MRA,the wavelet transform becomes the wavelet packet transform.
The surface roughness is decomposed by wavelet packet through the process described below.
Step 1 The random surface height z(x,y) is transformed into spectral domain using the wavelet packet transform. The height spectral function is given by S(kx,ky).
Step 2 A free wave number kd is chosen to split the roughness. Therefore,the height spectrum for zs(x,y) in (|kx≥kd|∪|ky≥kd|) is Ss(kx,ky),while that for zk(x,y) in |kx<kd|∩|ky<kd| is Sk(kx,ky). The surface height spectrum can be computed using Eq. (5).
Step 3 An inverse transform of the wavelet packet is used to transform Ss(kx,ky) into the height function zs(x,y) of small-scale roughness. Next,we judge whether the RMS height ss and correlation length ls of zs(x,y) are consistent with the ranges of validity of the SPM (kss<0.3, ss/ls<0.21)[21]. Otherwise,we repeat Step 2 and reselect the kd.
Step 4 When kd is determined,Ss(kx,ky) and Sk(kx,ky) can be calculated. Given that both scales of the roughness can be obtained by the inverse transform of the wavelet packet,the surface roughness is successfully divided into two parts.
Fig. 2 illustrates the surface roughness decomposition by wavelet packet.
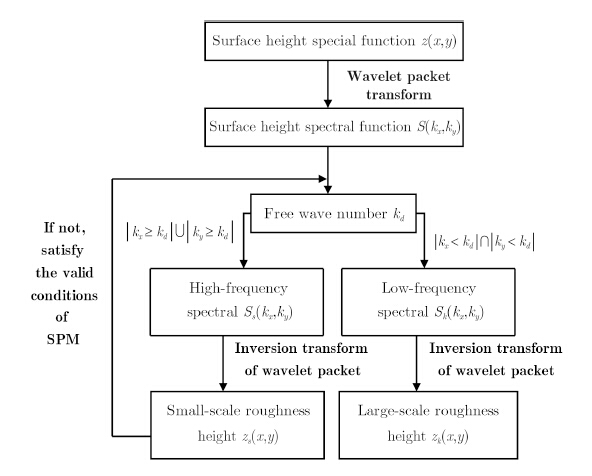
|
Fig.2 Decomposition of the two-scale roughness surface |
The far-zone equation of electromagnetic scattering is used to derive the formula of the MTSM. Following the Stratton-Chu equation[9],the far-zone scattered electric field is computed in terms of tangential electric and magnetic fields expressed as
| \[{E^s} = K{n_s} \times \int [(n \times E) - {\eta _s}{n_s} \times (n \times {\text{ }}H)]{{\text{e}}^{{\text{j}}{k_s}r \times {n_s}}}{\text{d}}S\] | (15) |
| $K = - {\rm j}{k_s}{{\rm e}^{ - {\rm j}{k_s}{R_0}}}/(4 {π} {R_0}) \hspace{95pt}$ | (16) |
where E and H are the tangential electric and magnetic fields,respectively; ns is the unit vector in the scattering direction; n is the surface normal unit vector; hs is the intrinsic impedance in the upper medium; S is the area of scattering cross section; j is the imaginary unit; ks is the wave number in the upper medium; r is the position vector of r; and R0 is the distance from the center of the illuminated area to the receiver. The scattered electric field in the upper medium can be expressed as
| ${E^{s}} \!=\! K{{n}_s} \! \times \!\! \int \!\! {[({{n}_1} \!\! \times \!\! E) \!-\! {\eta _1}{{n}_s} \! \times \! ({{n}_1} \!\! \times \!\! H)]} {{\rm{e}}^{{\rm j}{k_1}({{n}_s} - {{n}_i}){r}'}}{\rm{d}}S'$ | (17) |
where n1 is the normal unit vector of the upper medium,ni is the unit vector in the incident direction,S' is the scattering cross section of r',k1 is the wave number in the upper medium,and r' is the position vector of r'.
The phase factor of Eq. (17) can be written as
| ${k_1}({{n}_s} - {{n}_i}) \cdot {r}' = {q_x}x' + {q_y}y' + {q_z}z'$ | (18) |
where (x',y',z') is the Cartesian coordinate of r'. Next,qx,qy,and qz are respectively computed as
| $\left\{ \begin{array}{l} {q_x} = {k_1}(\sin {\theta _s}\cos {\varphi _s} - \sin \theta_i\cos \varphi_i)\\ {q_y} = {k_1}(\sin {\theta _s}\sin {\varphi _s} - \sin \theta_i\sin \varphi_i)\\ {q_z} = {k_1}(\cos {\theta _s} + \cos \theta_i) \end{array} \right.$ | (19) |
where qi and qs are the incident and scattering angles,respectively,and ji and js are the incident and scattering azimuth angles,respectively.
If we substitute k1(ns–ni)r' by Eq. (18),Eq. (17) can be rewritten as
| $\begin{aligned} {E^{s}} = & K{{n}_s} \times \int {\left[{{{n}_1} \times {E} - {\eta _1}{{n}_s} \times \left( {{{n}_1} \times {H}} \right)} \right]} \\ & .\exp \left( {{q_x}x' + {q_y}y' + {q_z}z'} \right){\rm{d}}S' \end{aligned}$ | (20) |
We then suppose $z' = {z'\!_k} + {z'\!_s}$ and compute Es as
| $\begin{aligned} E_{}^s = & K{{n}_s} \times \int {\left[{{{n}_1} \times E - {\eta _1}{{n}_s} \times \left( {{{n}_1} \times {H}} \right)} \right]} \\ & .\exp \left( {{\rm j}{q_x}x' + {\rm j}{q_y}y'} \right)\exp \left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} + {{z'\!\!_s}}} \right)} \right]{\rm d}S'\\ = & K{{n}_s} \times \int {B \cdot \exp \left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} + {{z'\!\!_s}}} \right)} \right]{\rm d}S'} \end{aligned}$ | (21) |
| $\hspace{5pt} B \! = \! \left[{{{n}_1} \! \times \! {E} \! - \! {\eta _1}{{n}_s} \! \times \! \left( {{{n}_1} \! \times \! {H}} \right)} \right]\exp \left( {{\rm j}{q_x}x' \!\! + \! {\rm j}{q_y}y'} \right)$ | (22) |
Obviously,B is irrelevant with z'. According to Taylor’s law,exp[jqz$\left( {{{z'\!\!_k}} + {{z'\!\!_s}}} \right)$] can be expressed as
| $\exp \left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} + {{z'\!\!_s}}} \right)} \right] = 1 + \sum\limits_{n{\rm{ = 1}}}^\infty {\frac{1}{n}{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} + {{z'\!\!_s}}} \right)} \right]}^n}} $ | (23) |
Thus,the scattering electric field Es is rewritten as
| $E_{}^s = K{{n}_s} \! \times \! \int \! {B \! \cdot \! \left(\!1 \!+\! \sum\limits_{{n \rm{= 1}}}^\infty {\frac{1}{n}{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} \!+\! {{z'\!\!_s}}} \right)} \right]}^n}}\!\right) {\rm d}S'} $ | (24) |
Meanwhile,the backscattering coefficient is computed as
| $\sigma _{pq}^o({\theta _i}) = \frac{{4 {π} {R_0^2}{\mathop{\rm Re}\nolimits} \left\{ {{\left\langle {{{\left| {E_{}^sE{{_{}^s}^*}} \right|}^2}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {{{\left| {E_{}^sE{{_{}^s}^*}} \right|}^2}} \right\rangle } {{\eta ^ * }_s}}} \right. } {{\eta ^ *_s }}}\right\} }}{{{A_0}{\mathop{\rm Re}\nolimits} \left\{ {{{{\left| {{E_0}} \right|}^2}} \mathord{\left/ {\vphantom {{{{\left| {{E_0}} \right|}^2}} {{\eta ^ * }_1}}} \right. } {{\eta ^ *_1 }}}\right\} }}$ | (25) |
where pq is the polarization manner,A0 is the illuminated area,Re{} is the real part operator,* denotes the complex conjugate,and $\left\langle {{{\left| {E_{}^sE{{_{}^s}^*}} \right|}^2}} \right\rangle $ is expressed as
| $\begin{array}{l} \left\langle {{{\left| {E_{}^sE{{_{}^s}^*}} \right|}^2}} \right\rangle = K{{n}_s} \times \int {B \cdot \exp \left[{{\rm j}{q_z}\left( {z'} \right)} \right]{\rm d}S'} \cdot K{{n}_s} \times \int {B \cdot \exp \left[{ - {\rm j}{q_z}\left( {z''} \right)} \right]{\rm d}S''} \\ \quad \quad \quad \quad \quad = \iint C\left\langle {\exp \left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} - {{z''\!\!\!_k}} + {{z'\!\!_s}} - {{z''\!\!\!_s}}} \right)} \right]} \right\rangle {\rm d}S'{\rm d}S''\\ \quad \quad \quad \quad \quad =\iint C \left\langle {\left(1 + \sum\limits_{n = 1}^\infty {\frac{1}{{n!}}{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} - {{z''\!\!\!_k}}} \right) + {\rm j}{q_z}\left( {{{z'\!\!_s}} - {{z''\!\!\!_s}}} \right)} \right]}^n}} \right)} \right\rangle {\rm d}S'{\rm d}S''\\ \quad \quad \quad \quad \quad =\iint C \left(1 + \sum\limits_{n = 1}^\infty {\frac{1}{{n!}}\left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} - {{z''\!\!\!_k}}} \right) + {\rm j}{q_z}\left( {{{z'\!\!_s}} - {{z''\!\!\!_s}}} \right)} \right]}^n}} \right\rangle }\right) {\rm d}S'{\rm d}S'' \end{array}$ | (26) |
In Eq. (26),$z'' = z''\!\!\!_{k} + z''\!\!\!_{s}$,$S''$ is the scattering cross section of r'',and C is independent of z' and z''. If we expand the n-order terms in Eq. (26),then we obtain the equation
| $\begin{aligned} \left\langle {{{\left| {E_{}^sE{{_{}^s}^*}} \right|}^2}} \right\rangle = & \iint C \left(1 + \sum\limits_{n = 1}^\infty {\frac{1}{{n!}}[\left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} - {{z''\!\!\!_k}}} \right)} \right]}^n}} \right\rangle + \cdots + C_n^k\left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} - {{z''\!\!\!_k}}} \right)} \right]}^{n - k}}{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_s}} - {{z''\!\!\!_s}}} \right)} \right]}^k}} \right\rangle + } \cdots \right. \\ & + \left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_s}} - {{z''\!\!\!_s}}} \right)} \right]}^n}} \right\rangle] \Biggr){\rm d}S'{\rm d}S'' \end{aligned}$ | (27) |
Given that the large-scale roughness surface zk is independent of the small-scale roughness surface zs,the ensemble average of the cross-term is 0 in Eq. (27)[9]. Thus,we obtain the equation
| $\left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} - {{z''\!\!\!_k}}} \right)} \right]}^{n - k}}{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_s}} - {{z''\!\!\!_s}}} \right)} \right]}^k}} \right\rangle = 0,k = 1,2,\cdots ,n - 1$ | (28) |
| $\begin{aligned} \left\langle {{{\left| {E_{}^sE{{_{}^s}^*}} \right|}^2}} \right\rangle & = \iint C \left(1 + \sum\limits_{n = 1}^\infty {\frac{1}{{n!}}[\left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} - {{z''\!\!\!_k}}} \right)} \right]}^n}} \right\rangle + } \left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_s}} - {{z''\!\!\!_s}}} \right)} \right]}^n}} \right\rangle]\right){\rm d}S'{\rm d}S''\\ & = \iint C \left(1+ \sum\limits_{n = 1}^\infty {\frac{1}{{n!}}\left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} - {{z''\!\!\!_k}}} \right)} \right]}^n}} \right\rangle } \right){\rm d}S'{\rm d}S'' + \iint C\sum\limits_{n = 1}^\infty {\frac{1}{{n!}}\left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_s}} - {{z''\!\!\!_s}}} \right)} \right]}^n}} \right\rangle } {\rm d}S'{\rm d}S''\\ & = \iint C \exp \left[{{\rm j}{q_z}\left( {{{z'\!\!_k}} - {{z''\!\!\!_k}}} \right)} \right]{\rm d}S'{\rm d}S'' + \iint C\sum\limits_{n = 1}^\infty {\frac{1}{{n!}}\left\langle {{{\left[{{\rm j}{q_z}\left( {{{z'\!\!_s}} - {{z''\!\!\!_s}}} \right)} \right]}^n}} \right\rangle } {\rm d}S'{\rm d}S'' \end{aligned}$ | (29) |
The first term in Eq. (29) is the scattering field of large-scale roughness,which is calculated by KM. The second term represents the scattering field of small-scale roughness,which can be simulated by SPM without the zero-order solutions. Given that the first-order solutions of SPM represent the surface scattering,the second-order and the other higher-order solutions represent the complex volume scattering. We skip the volume scattering and simply calculate the first-order solutions of SPM. As a result,we substitute $\left\langle {{{\left| {E_{}^sE{{_{}^s}^*}} \right|}^2}} \right\rangle $ into Eq. (25) by Eq. (29). The scattering coefficient of the two-scale surface can be written as
| $\sigma _{pq}^o({\theta _i}) = {\sigma _{pq}}{( {\theta _i})^{\rm{KA}}} + {\sigma _{pq}^{(1)}}{({\theta _i})^{\rm{SPM}}}$ | (30) |
where${\sigma _{pq}}{( {\theta _i})^{\rm{KA}}}$ is the scattering contribution of large-scale roughness at qi,and ${\sigma _{pq}^{(1)}}{({\theta _i})^{\rm{SPA}}}$ is the first-order solutions of SPM for small-scale roughness. Given that the small-scale roughness lays on the top of the large-scale roughness (i.e.,the tilting effect),we calculate the ensemble average of SPM to correct such effect. Thus,we obtain the equation
| $\sigma _{pq}^o({\theta _i}) = {\sigma _{pq}}{( {\theta _i})^{{\rm{KA}}}} + \left\langle {{\sigma _{pq}^{(1)}}{{({\theta _i})}^{{\rm{SPM}}}}} \right\rangle $ | (31) |
Then,we calculate the solutions of ${\sigma _{pq}}{( {\theta _i})^{{\rm{KA}}}}$$\left\langle {{\sigma _{pq}^{(1)}}{{({\theta _i})}^{{\rm{SPM}}}}} \right\rangle $.
3.2 Kirchhoff scattering fieldThe KM applies tangent plane approximation to calculate the surface fields,which is only valid if the radius of the curvature is larger than a wavelength. When the surface roughness is relatively large (kl>6 andl2>2.76sl),the KM is reduced to the Geometric Optics model by phase approximation,and the backscattering coefficient is computed as Ref. [13]
| ${\sigma _{pq}}{( {\theta _i})^{{\rm{KA}}}} = \frac{{{{\left| {{\Gamma _{pq}}(0)} \right|}^2}}}{{2{m^2}{{\cos }^4}{\theta _i}}}\exp \left( - \frac{{{{\tan }^2}{\theta _i}}}{{2{m^2}}}\right)$ | (32) |
where m is the average slope,$m = \sqrt 2 {s \mathord{\left/ {\vphantom {s l}} \right. } l}$ for the Gaussian surface,and Gpq(0) is the Fresnel reflection coefficient in the normal direction (qi=0). If p≠q,${\sigma _{pq}}{( {\theta _i})^{{\rm{KA}}}} = 0$,Gpq(0) is computed as
| ${\Gamma _{{\rm{hh}}}}(0) = {\Gamma _{{\rm{vv}}}}(0) = \left| {\frac{{1 - \sqrt \varepsilon }}{{1 + \sqrt \varepsilon }}} \right|$ | (33) |
where e is a dielectric constant.
When 0.05l<s<0.15l,l>l and m<0.25,the KM is reduced to the Physic Optics model by scalar approximation. The backscattering coefficient is then computed as Ref. [13]
| $\begin{aligned} {\sigma _{pq}}{( {\theta _i})^{\rm{KA}}} = & {k^2}{\cos ^2}{\theta _i}{\Gamma _{pq}}({\theta _i})\exp ( - {(2ks\cos {\theta _i})^2})\\ & \cdot \sum\limits_{n = 1}^\infty {\frac{{{{(2ks\cos ({\theta _i}))}^{2n}}}}{{n!}}} {W^n}(2k\sin ({\theta _i}),0) \end{aligned}$ | (34) |
where ${W^n}(2k\sin {\theta _{i}},0)$ is the roughness spectrum of the surface that is related to the n-th power of the surface correlation function by the Fourier transform. For the Gaussian surface,${W^n}(2k\sin {\theta _{i}},0)$ is expressed as
| ${W^n}(2k\sin ({\theta _i}),0) = \frac{{{l^2}}}{n}\exp \left\{ - \frac{{{{(kl\sin {\theta _i})}^2}}}{n}\right\} $ | (35) |
As stated above,Gpq(qi) is the Fresnel reflection coefficient,and is denoted as
| ${\Gamma _{\rm hh}}({\theta _i}) = {\left| {\frac{{\cos {\theta _i} - \sqrt {\varepsilon - {{\sin }^2}{\theta _i}} }}{{\cos {\theta _i} + \sqrt {\varepsilon - {{\sin }^2}{\theta _i}} }}} \right|^2} \hspace{12pt}$ | (36) |
| ${\Gamma _{{\rm{vv}}}}({\theta _i}) = {\left| {\frac{{\varepsilon \cdot \cos {\theta _i} - \sqrt {\varepsilon - {{\sin }^2}{\theta _i}} }}{{\varepsilon \cdot \cos {\theta _i} + \sqrt {\varepsilon - {{\sin }^2}{\theta _i}} }}} \right|^2}$ | (37) |
In the two-scale surface,given that the large-scale roughness is covered by small-scale roughness,the Fresnel reflection coefficient in KA must be modified as[22]
| $\begin{aligned} \left\langle {{\Gamma _{pq}}} \right\rangle = & {\Gamma _{pq}}({\theta _i})\biggr[1 - 2k\sin {\theta _i}\\ & \cdot \int\nolimits_{ - \infty }^\infty \!\! \int\nolimits_{ - \infty }^\infty \! W(u \!-\! k\sin {\theta _i},v) \\ & \times \! {K_{pq}}(u,v){\rm{d}}u{\rm{d}}v \biggr] \end{aligned}$ | (38) |
where Gpq is the corrected Fresnel reflection coefficient,Kpq(u,v) is the KM filed coefficient,and W(u–ksinqi,v) is the roughness spectrum.
3.3 Small perturbation scattering fieldThe SPM is valid for the rough surface with a small RMS height and small slope; its effective applying ranges are ks<0.3 and s/l<0.21. According to the former analysis in Eq. (30),the first-order solutions of SPM is expressed as
| ${\sigma _{pq}^{(1)}}{({\theta _i})^{{\rm{SPM}}}} = 8{k^4}{s^2}{\cos ^4}{\theta _i}{\left| {{a_{pq}}({\theta _i})} \right|^2}W(2k\sin {\theta _i},0)$ | (39) |
where apq(qi) is the polarized amplitude coefficient in SPM,whereas
| $\quad\quad{a_{{\rm{hh}}}}({\theta _i}) = \frac{{{\varepsilon _s} - 1}}{{{{\left(\cos {\theta _i} + \sqrt {{\varepsilon _s} - {{\sin }^2}{\theta _i}} \right)}^2}}}$ | (40) |
| $\quad\quad{a_{{\rm{vv}}}}({\theta _i}) = ({\varepsilon _s} \! - \! 1)\frac{{{{\sin }^2}{\theta _i} \! - \! {\varepsilon _s}(1 \! + \! {{\sin }^2}{\theta _i})}}{{{{\left({\varepsilon _s}\cos {\theta _i} \! + \! \sqrt {{\varepsilon _s} \! - \! {{\sin }^2}{\theta _i}} \right)}^2}}}$ | (41) |
In the two-scale surface,the small-scale roughness lays on the large-scale roughness. Therefore,the tilting effect must be corrected. In the next step,zkx and zky are assumed to be the slopes of the large-scale roughness (zk) in the x-axis and y-axis,respectively,while
| $P({z_{x2}}) = \frac{{{{l}_2}{{n}_2} \cdot {z}}}{{({{l}_1}{{n}_1} + {{l}_2}{{n}_2} + {{l}_3}{{n}_3}) \cdot {z}}} = \frac{{{{l}_2}{{n}_2} \cdot {z}}}{L}$ | (42) |
| $L = ( {{l}_1}{{n}_1} + {{l}_2}{{n}_2} + {{l}_3}{{n}_3}) \cdot {z} \hspace{73pt}$ | (43) |
In the direction of incident qi, P(zx2) is expressed as
| ${P_{\theta_i} }({z_{x2}}) = \frac{{{{l}_2}{{n}_2} \cdot {{k}_i}}}{{( {{l}_1}{{n}_1} + {{l}_2}{{n}_2} + {{l}_3}{{n}_3}) \cdot {k_i}}} = \frac{{{{l}_2}{{n}_2} \cdot {{k}_i}}}{{{L_{\theta_i} }}}$ | (44) |
| ${L_{\theta_i}} = ({{l}_1}{{n}_1} + {{l}_2}{{n}_2} + {{l}_3}{{n}_3}) \cdot {{k}_i}\hspace{73pt}$ | (45) |
where ki is the unit vector in the incident direction. From Eqs. (42) to (45),we obtain the following:
| ${P_{\theta_i}}({z_{x2}}) = \frac{L}{{{L_{\theta_i} }}}\cos {\theta _i}(1 + {z_{x2}}\tan {\theta _i})P({z_{x2}})$ | (46) |
Given that only three roughnesses are observed in Fig. 3,the sum of the probability distribution function is 1,that is,
| $\sum\limits_{m = 1}^3 {{P_{\theta_i}}({z_{xm}})} = 1$ | (47) |

|
Fig.3 Geometric explanation of the gradient’s probability distribution[23] |
Therefore,
| $\frac{L}{{L_{\theta_i }}}\cos {\theta _i} = 1$ | (48) |
As a result,in the two-dimensional random surface,${P_{{\theta _{i}}}}$(zkx,zky) can be written as
| ${P_{\theta_i} }({z_{kx}},{z_{ky}}) = (1 + {z_{kx}}\tan {\theta _i})P({z_{kx}},{z_{ky}})$ | (49) |
where P(zkx,zky) is the probability distribution function of the large-scale roughness and follows a (0,$\sigma _{zk}^2$) Gaussian distribution given by
| $P({z_{kx}},{z_{ky}}) = \frac{1}{{2\pi \sigma _{Zk}^2}}\exp \left\{ { - \frac{{z_{kx}^2 + z_{ky}^2}}{{2\sigma _{Zk}^2}}} \right\}$ | (50) |
Therefore,the second term in Eq. (31) is expressed as[23]
| $\begin{aligned} \! \lt \!\! {\sigma _{pq}^{(1)}}\!({\theta _i}) \!\! { > ^{\rm{SPM}}} \!=\!\! & \int\nolimits_{ - \infty }^\infty \!\! {\int\nolimits_{ - \cot {\theta _i}}^\infty \!\!\!\! {{{(p \! \cdot \! p')}^4}{\sigma _{pq}^{(1)}}({{\theta '}_i})} } \\ & \cdot (1 \!+\! {z_{kx}} \! \tan \! {\theta _i}) P({z_{kx}},{z_{ky}}){\rm d}{z_{kx}}{\rm d}{z_{kx}} \end{aligned}$ | (51) |
where p and p' are the unit polarized vectors of the basic and local coordinate systems,respectively,and is the local incident angle. To avoid the self-shadowing effect,the integral limit of zkx in Eq. (51) is within the range of –cotqi to $\infty$.
4 ValidationThe AIEM,which is the improvement of IEM,is adopted to verify the MTSM. The AIEM has the widest range of applicability; thus,it is the most popular method for calculating the surface scattering. In this model,the single scattering term is expressed as
| $\begin{aligned} {\sigma _{pqs}} = & \frac{{{k_1^2}}}{2}\exp ( - {s^2}({k_z^2} + {k_{sz}^2}))\\ & \cdot \sum\limits_{n = 1}^\infty {\frac{{{s^{2n}}}}{{n!}}{{\left| {{I_{pq}^n}} \right|}^2}} {W^n}({k_{sx}} - {k_x},{k_{sy}} - {k_y}) \end{aligned} $ | (52) |
| $\begin{aligned} I_{pq}^n = & {({k_{sz}} \!+\! {k_z})^n}{f_{pq}}\exp ( - {s^2}{k_z}{k_{sz}})\\ & + \frac{{{{( \!{k_{sz}})}^n}{F_{pq}}(\! - {k_x},- {k_y}) \!+\! {{(\!{k_z})}^n}{F_{pq}}(\! - {k_{sx}},- {k_{sy}})}}{2} \end{aligned} $ | (53) |
where Wn(ksx–kx,ksy–ky) is the roughness spectrum of the surface that is related to the n-th power of the surface correlation function by the Fourier transform, and fpq and Fpq are the Kirchhoff and complementary field coefficients,respectively. In addition,kz=kcosqi,ksz=kcosqs,kx=ksinqi
·cosji,ksx=ksinqscosjs,ky=ksinqisinji,and ksy=ksinqssinjs.
The inputs of simulations are set as follows: frequency f=5.63 GHz,complex dielectric constant es=19.54+3.08i,and incident angle qi $ \in $ [10°,70°]. Three different Gaussian surfaces (ks=0.354,1.061,2.352; kl=8.21) are assumed to test the MTSM. The selected wave number kd for splitting the roughness in MTSM must satisfy the two requirements given by
| $\quad\quad\quad\quad {s_s} = \frac{s}{5},\quad ks \lt 1.5$ | (54) |
| $\quad\quad\quad\quad k{s_s} = 0.3,ks \ge 1.5$ | (55) |
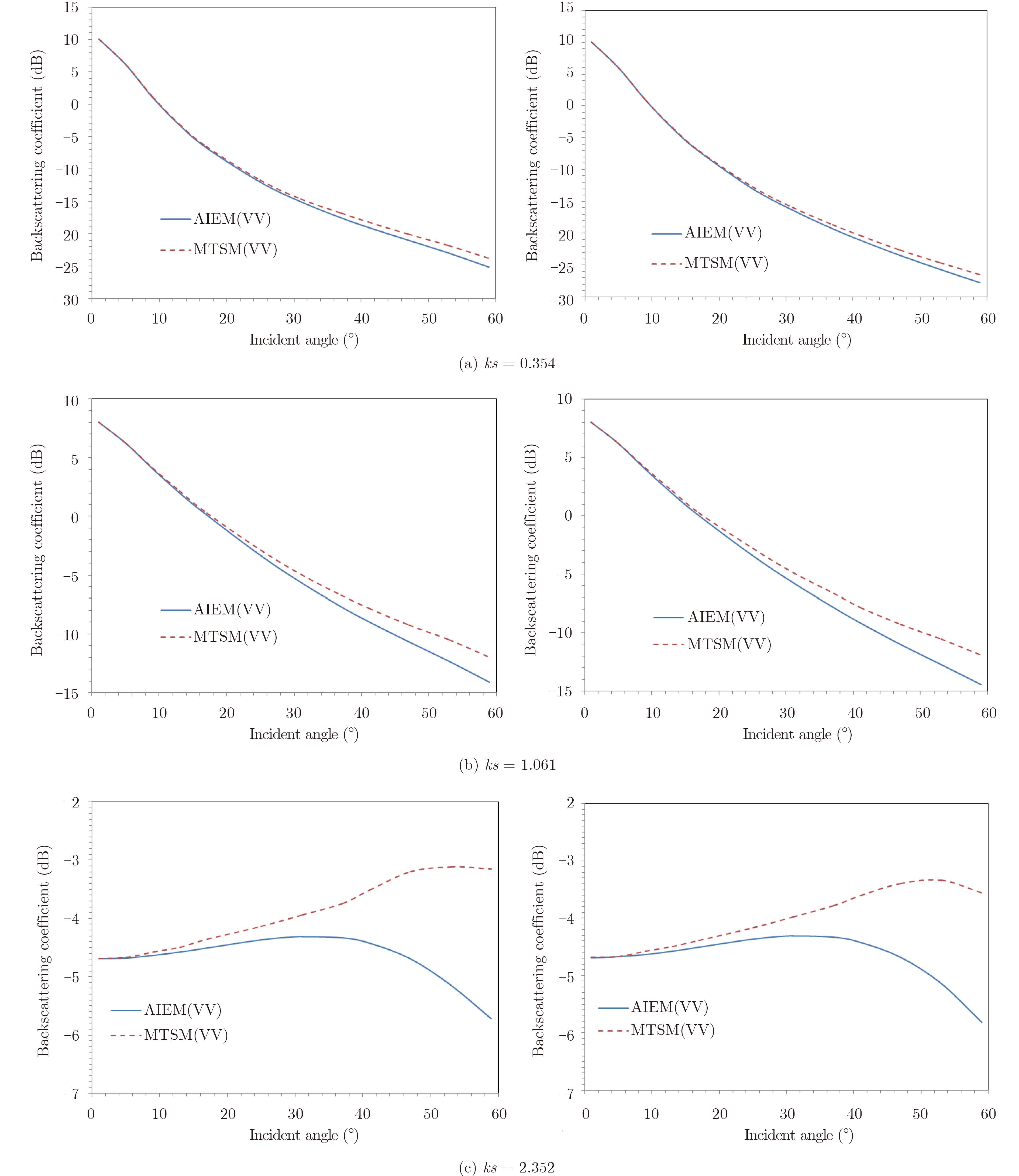
Fig. 4 shows the scatter plots of the backscattering coefficients estimated using the MTSM versus AIEM on three different roughness surfaces. As can be seen,the MTSM is in favorable agreement with the AIEM at small incident angles. When qi increases,the difference between these two models becomes larger,reaching the largest value of 2.561 dB at qi= 60° in VV polarization. When the surface roughness is small (ks= 0.354),the MTSM provides very accurate predictions,presenting less than 0.68 dB difference with the AIEM for both VV and HH polarizations. As the surface roughness increases,the results of the MTSM move far from those of the AIEM.
Fig. 4(c) shows that the difference in the results of these two models exceeds 2 dB for both polarizations when qi>45°. The estimation of the MTSM in VV polarization,instead of HH,is slightly closer to that of the AIEM,indicating that the polarization manner has slightly influenced the MTSM. Therefore,the MTSM can achieve favorable accuracy when both the incident angle and surface roughness are small.
|
Fig.4 Comparison of the backscattering coefficients predicated by the AIEM and MTSM (Here, kl = 8.21, qi Є [10°, 70°] and es = 19.54+3.08i for different roughnesses) |
This paper proposed a new model (MTSM) for describing the backscattering for a Gaussian-distributed rough surface. The surface height function z(x,y) is transformed into a frequency domain by wavelet packet,and the surface height spectrum is split into two parts. The large-scale roughness corresponding to the low frequency portion of the spectrum (k<kd) assumes that the KM adequately describes the scattering from these height excursions. The small-scale roughness is represented by the high frequency portion of the total height spectrum (k≥kd),which is described by a first order SPM. The key parameter kd for spectral dichotomy is determined using Eq. (49). The tilting effect caused by the large-scale roughness has been corrected,and the backscattering of the MTSM represents the sum of both scale roughness surfaces. From the numerical experiments,several conclusions are drawn.
(1) Large- and small-scale roughnesses cannot be easily measured using the traditional TSM. Hence,wavelet packet transform is used to split the surface height spectrum into two parts,thereby increasing the usefulness of the TSM in practice.
(2) The simulations of the AIEM and MTSM are in excellent agreement when both the incident angle and surface roughness are small. The different polarization manner has a slight influence on the MTSM.
(3) The MTSM is established to describe the electromagnetic scattering properties of a typical two-scale land surface. This model has only been tested by numerical simulation using the AIEM model. The application of this model to natural surfaces and the ranges of validity of its surface roughness should be investigated further in future research.
| [1] | Valenzuela G R. Depolarization of EM waves by slightly rough surface[J]. IEEE Transactions on Antennas and Propagation, 1967, 15(4): 552-557.( 1) 1) |
| [2] | Ulaby F T, Batlivala P, and Dobson M. Microwave backscatter dependence on surface roughness, soil moisture and soil texture: Part 1-Bare soil[J]. IEEE Transactions on Instrumentation and Measurement, 1978, 16(4): 286-295.( 1) 1) |
| [3] | Jin Y Q. Theory and Method of Numerical Simulation of Composite Scattering from the Object and Randomly Rough Surface[M]. Beijing: Science Press , 2008: 5-15.( 1) 1) |
| [4] | Beckmann P A and Spozzochino T. The Scattering of Electromagnetic Waves from Rough Surface[M]. New York: Macmillan Press, 1968: 20-35.( 1) 1) |
| [5] | Fung A K. Theory of cross-polarized power returned from a random surface[J]. Applied Science Research, 1968, 18(1): 50-60.( 1) 1) |
| [6] | Fung A K, Li Z, and Chen K S. Backscattering from a randomly rough dielectric surface[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(2): 356-369.( 2) 2) |
| [7] | Wu T D, Chen K S, Shi J C, et al.. A transition model for the reflection coefficient in surface scattering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(9): 2040-2050.( 1) 1) |
| [8] | Wu T D and Chen K S. A reappraisal of the validity of the IEM model for backscattering from rough surface[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4): 743-753.( 1) 1) |
| [9] | Ulaby F T, Moore P K, and Fung A K. Microwave Remote Sensing, Vol Ⅱ: Microwave Remote Sensing Fundamentals and Radiometry[M]. London: Addison Wesley Publishing Company Press, 1981: 6-18.( 3) 3) |
| [10] | Brown G S. Backscattering from a Gaussian distributed perfectly conducting rough surface[J]. IEEE Transactions on Antennas and Propagation, 1978, 26(3): 472-482.( 1) 1) |
| [11] | Burrows M L. A reformulated boundary perturbation theory in electromagnetism and its application to a sphere[J]. Canadian Journal of Physics, 1967, 45(5): 1729-1743.( 1) 1) |
| [12] | Wright J. A new model for sea clutter[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(2): 217-223.( 1) 1) |
| [13] | Burrows M L. On the composite model for rough surface scattering[J]. IEEE Transactions on Antennas and Propagation, 1973, 21(2): 241-243.( 3) 3) |
| [14] | Mario L. Applied Stochastic Processes[M]. New York: John Wiley and Sons Press, 1996: 55-62.( 1) 1) |
| [15] | Fang Z B. Stochastic Processes[M]. Beijing: Science Press, 2011: 10-25.( 1) 1) |
| [16] | Beckmann P. Scattering by non-Gaussian surfaces[J]. IEEE Transactions on Antennas and Propagation, 1975, 21(2): 169-175.( 1) 1) |
| [17] | Chui C K. An Introduction to Wavelets[M]. New York: Academic Press, 1992: 22-34.( 2) 2) |
| [18] | Hilton M L, Jawerth B D, and Sengupta A. Compressing still and moving images with wavelets[J]. Multimedia System, 1994, 2(3): 218-227.( 1) 1) |
| [19] | Nielsen N H and Wickerhauser M V. Wavelets and time-frequency analysis[J]. Proceedings of the IEEE, 1996, 84(4): 523-540.( 1) 1) |
| [20] | Strang G and Nguyen T Q. Wavelets and Filter Banks[M]. Wellesley: Wellesley-Cambridge Press, 1996: 103-134.( 1) 1) |
| [21] | Fung A K. Exact Scattering from a Known Randomly Rough Surface[M]. Switzerland: URSI Commission Press, 1974: 2-8.( 1) 1) |
| [22] | Valenzuela G R. Theories for the interaction of electromagnetic and oceanic waves - a review[J]. Boundary-Layer Meteorology, 1978, 13(1): 61-85.( 1) 1) |
| [23] | Jin Y Q. Remote Sensing Theory of Electromagnetic Scattering and Thermal Emission[M]. Beijing: Science Press, 1993: 87-102.( 3) 3) |


