Radar has become a powerful tool in inferring the location, shape and reflectivity of targets under investigation by transmitting an electromagnetic signal with transmitter(s), and post-processing the echo of transmitting signal after experiencing the interaction with probed targets^{[1, 2]}. Such technology has found its valuable applications in many application fields including subsurface sensing, security management, biomedical imaging, to name a few.

Over past decades, an amount of excellent imaging algorithms for post-processing GPR/TWI data has been developed^{[3, 4]}, for instance, the filtered back-propagation algorithm^[5], the phase-shift imaging algorithm^[6], the time-reversal imaging algorithm^[7], the resolution-enhanced imaging algorithm based on compressive sensing^[8], and so on. Almost all of methods mentioned above rely on the use of Born approximation^{[9, 10]}, which leads to a linearized imaging approach, since it does not account for the multiple-scattering effect between the electromagnetic wavefield and objects under investigation. Therefore, the Born-based imaging approach is theoretically guaranteed to be used for treating weak scattering objects. Consequently, when the probed object is not very weak, the radar image produced by performing the Born-based imaging approach usually exhibits some multipath ghosts (i.e., the false target)^{[11, 12, 13, 14, 15, 16, 17]}, and thus impairs the reliability of identifying real targets at the same time. Recently, it has been observed that the multipath ghost is aspect dependent^[18], which implies that the shape and position of ghosts will be different with different measurement aperture. Inspired by this observation, several methods of mitigating the multipath ghost have been proposed, which compounds, in the manner of multiplication, images achieved from different sub-apertures^{[18, 19]}.

This letter presents a novel concept of mitigating the multipath ghost and enhancing the resolution of real targets at the same time, involved in the problem of GPR (Ground Penetrating Radar) and TWI (Through-Wall Imaging) imaging. To this end, we model for the first time the reflectivity of probed objects as a probability function with a normalized factor, which means that the radar imaging is reformulated into the one consisting of retrieving the probability function. Furthermore, the concept of the random sub-aperture is incorporated into our imaging procedure. The random sub-aperture is formed by randomly picking up some measurement locations from the complete observation aperture, which implies that multiple random sub-apertures can be created, and thus multiple probability functions (i.e., radar images) can be produced. Apparently, it is natural that the final radar image can be regarded as a joint probability distribution, which is the product of radar images achieved from multiple random sub-apertures. We would like to emphasis that the random sub-aperture adopted in this letter is advantageous over traditional overlapped sub-aperture used in Ref. ^{[18, 19]}, in the sense that (a) it is more flexible in creating the sub-aperture configuration, and (b) it is capable of avoiding the drawback of the traditional sub-aperture^{[2, 18, 19]} that some real targets will be missing when they are missing in some radar image corresponding to some radar sub-aperture, due to the multiplication operation of multiple radar images, as demonstrated in Section 4.

The rest of this letter is organized as follows: Section 2 discusses the probability model for the problem of GPR and TWI imaging, and illustrates the operational principle of proposed imaging methodology. Afterwards, a selected number of numerical experiments are conducted to demonstrate the state-of-art performance of proposed methodology in Section 3, where the simulation data is achieved from running a commercial software GPRMax 2.5, a full-wave solver to the Maxwell’s equations. Finally, Section 4 summarizes this letter.

To illustrate the working principle of the proposed methodology, we restrict ourselves into the Two-Dimensional (2D) scalar case. However the proposed methodology and associated results can be generalized and applicable to more sophisticated imaging scenarios, such as, 3D and full-vector case in inhomogeneous media. We consider two popular imaging configurations, i.e, the GPR configuration (Fig. 1(a)), and TWI configuration (Fig. 1(b)). Referring to Fig. 1(a) and Fig. 1(b), an antenna is used to sequentially emit TM-polarized pulse ${u^{{\rm{inc}}}}(r;{r_{\rm{R}}})$, and receive the echoes after its interaction with objects embedded in the investigation domain D_inv. The antenna is located in the observation domain (denoted as $\Gamma $) exterior to the investigation domain D_inv (an inaccessible region). Additionally, this measurement line at y=y_m is denoted by $\Gamma $. Throughout this paper, we use the terminology and notation commonly employed in microwave imaging problem; moreover, a time-dependence factor e^-iwt is used and suppressed.

Fig. 1

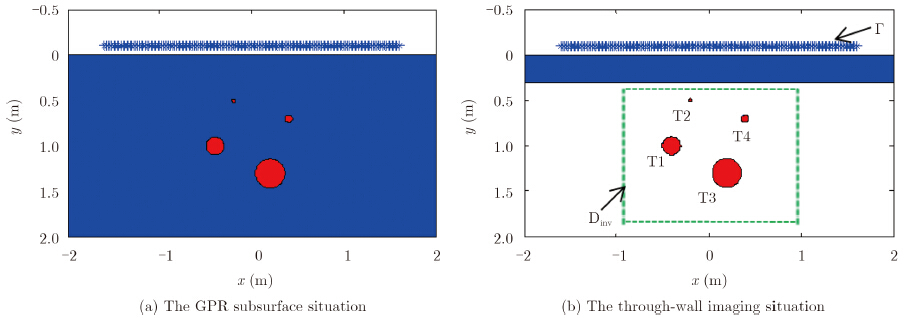Fig. 1  The sketched map of the probed scene populated by four metallic cylinders (Here, four metallic targets denoted as T1, T2, T3 and T4 are embedded into a half-space medium (a) or behind a homogeneous wall (b) respectively)

Under so-called Born approximation, the relation between the scattering data ${u^{{\rm{sca}}}}({r_{\rm{R}}}, \omega )$ acquired at ${r_{\rm{R}}} = ({x_{\rm{R}}}, {y_{\rm{R}}}) \in \Gamma $ and the contrast function of probed objects inside the investigation domain D_inv reads^[20]:

where the contrast function of probed objects is defined by $\chi ={{{k}^{2}}}/{k_{0}^{2}}\;-1$; and k and ${{k}_{0}}={\omega }/{c}\;$ are the wavenumbers of the object and background medium, respectively. $n({{r}_{\rm{R}}}, \omega )$ indicates the errors accounting for measurements noise and others. Moreover, $G({r}, {r}')$ is a 2D Green’s function, whose detailed representation can be found in our previous work, i.e, Ref. ^[3], and are not provided here due to limited paper space. Additionally, the operational frequency range is $\omega \in [{\omega _{{\rm{min}}}}, {\omega _{{\rm{max}}}}]$.

This letter provides a novel interpretation for Eq. (1) in the context of probability. We would like to treat the location ${r}'$ as a random variable, which implies that the target happens to be at this location in the random manner. Furthermore, the contrast function ${χ} ({r}')$ is regarded as a probability density function for the random variable ${r}'$, which describes the probability of targets appearing at ${r}'$. Strictly speaking, to meet with the definition of probability function, the probability function should be defined as

To avoid too much notations, we still refer to $\chi ({r}')$ as the probability function since this treatment has no effects on the implementation of imaging procedure and the quality of final imaging results. In this way, the $k_0^2G({r_{\rm{R}}}, r';\omega )\cdot {{u}^{\rm{inc}}}({r}')$ is a random quantity charactering the probability of the interaction between the incident wave and the objects. In addition, the radar data ${{u}^{\rm{sca}}}({{{r}}_{\rm{R}}};{ω} )$ is understood as the expectation value of ${} k_{0}^{2}G({{{r}}_{\rm{R}}}, {r}'; {ω} ){{u}^{\rm{inc}}}({r}')$ with respect to the probability function $\chi ({r}')$, i.e,

Now, the original radar imaging problem Eq. (1) is reformulated into the one which aims at retrieving the probability function $\chi ({r}')$.

It is noted that the probability will be different for different radar viewing angle, since the radar with different viewing angle has different ability of detecting objects. In this sense, the final radar image can be treated as a joint probability function from multiple images associated with different radar view angles. Motivated by this observation, we explore the concept of random sub-aperture in our imaging procedure. Specifically, M random sub-apertures can be created, where each one is from randomly picking up observation locations from the entire radar aperture. Accordingly, M probability functions, ${\chi _m}(r')$, m=1, 2, $\cdots $, M, can be produced. Consequently, the final radar imaging $\chi ({r}')$ corresponds to the joint probability function of ${\chi _m}(r')$, m=1, 2, $\cdots $, M, in particular,

In this section, numerical simulations are conducted in two imaging scenario, i.e, GPR (Fig. 1a) and TWI (Fig. 1b), to evaluate the validity of the proposed method, where the input data for simulations is achieved by running a commercial software GPRMax 2.5, a full-wave solution to the Maxwell equations. For numerical implementations, the 2-D investigation domain D_inv=1.6 m×1.6 m for GPR application and D_inv=1.6 m×1.5 m for TWI application has been discretized into square pixels with size of 0.02 m×0.02 m. The complete measurement line with the length of L=3.2 m is sampled with a uniform step of 0.02 m, which means there are 161 pairs of transmitters and receivers in total. The transmitting signal is a 'ricker' wavelet with center frequency f₀=1 GHz, time duration T=40 ns and time interval dt=11.793 ps. Accordingly, the operational frequency range is [100, 3500] MHz, which is sampled with a step of 50 MHz. All simulations are performed in a personal computer with the configuration of 8 GB access memory, I7-2600 central processing unit, and a Matlab 7.9 environment.

In this subsection, we examine the performance of proposed imaging methodology in the typical setup of GPR imaging as illustrated in Fig. 1(a), where the sensor is located in free-space while the targets are embedded into the lower part of half-space medium with the relative permittivity being 6. The distance between the air-ground interface and the measurement line is 0.1 m, and four metallic cylinders are located at (-0.4, 1.0) m, (-0.2, 0.5) m, (0.2, 1.3) m, and (0.4, 0.7) m, with the radius being of 0.1 m, 0.02 m, 0.16 m and 0.04 m, respectively. Before starting imaging procedure, the direct wave from the reflection at the air-ground interface is removed by operating the mean-value filter on GPR raw data.

First, the result achieved by using the whole-aperture data is shown in Fig. 2. It can be observed from this figure that four targets are seriously surrounded by the false targets, especially below the line of y=1.2 m, and it is pretty a risk in distinguishing real targets from false targets. Note that the ghost is a little bit more away from the sensors than real targets and spreads into a big clutter, which makes sense since the multipath of wavefield between targets implies that the wave has some tails after direct-arrival waves. As for the ghosts spread into a big clutter, this is because that the ghosts' locations are dependent on the measurement configuration. Therefore, for each couple of transmitter and receiver, there is a clutter of ghosts closely around the true object, and the size of clutter depends strongly on the radar viewing angle.

Fig. 2

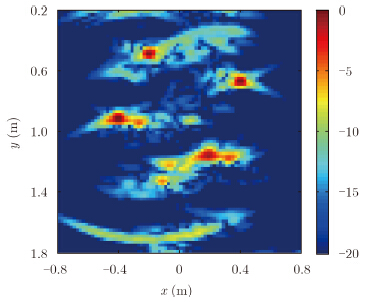Fig. 2  Reconstruction with whole aperture

Second, we perform the GPR imaging with the configuration of sub-array adopted in Ref. [21], where the whole aperture is divided into seven sub-aperture which has a length of 0.8 m and the overlap is 0.4 m between adjacent sub-apertures. The corresponding results are reported in Fig. 3, where Figs. 3(a)-3(g) correspond to seven sub-apertures; while Fig. 3(f) is the product of these seven images. Comparing these results shown in Fig. 2 and Fig. 3, we can draw two conclusions immediately, in particular, (a) the location of the identified real objects is independent on the radar view angle, if they can be observed by GPR. (b) the real object is dragged with a clutter of ghost, and the shape and position of clutter of ghosts depends strongly on the sub-aperture, as mentioned previously. Invoked by these two conclusions, as guided by Eq. (4), we multiply the images achieved by all sub-apertures and the result is shown in Fig. 3(h). Comparing Fig. 3(h) with Fig. 2, we can see clearly that the ghost has been significantly impaired while the real targets are still clear. Nonetheless, note that two real targets are missing, which arises from a fact that the multiplication operation of multiple radar images associated with multiple sub-apertures will suppress those weak targets, even clear them out, when some real targets are missing in some of these images. So, the selection of measurement configuration should be careful, since it plays an important role of getting a good result.

Fig. 3

Fig. 3  Results with sub-arrays adopted in Ref. [21]

Third, to overcome the drawback mentioned above, we adopt the random sub-aperture technique. The random sub-aperture composed of sensors selected randomly or sub-aperture in the following. Fig. 4 shows the results with five random sub-apertures and each random sub-aperture is assigned with a possibility of 0.2. Here, the probability means the one when the antenna element of entire measurement aperture is picked up in the random manner. By multiplying the five images obtained from five random apertures, the result is shown in Fig. 4(f). Comparing Fig. 4 with Fig. 3, we can see that there is no missing real targets due to the use of random sub-aperture, and thus the multiplication operation can suppress significantly ghosts and enhance real targets very well, without suppressing the real targets.

Fig. 4

Fig. 4  Reconstruction with five random sub-apertures

Finally, we examine the effect of image performance from changing the number of antenna elements for random sub-apertures or the possibility of random sub-aperture. The results for different possibility of random sub-aperture are shown in Fig. 5, from which we can see that the real targets will be enhanced more and more, and the clutter of ghosts will be weaker and smaller with the increasing probability of random sub-apertures over the range of [0.05, 0.2]. Generally, we can safely say that the random sub-aperture is more flexible and robust than traditional sub-array technique.

Fig. 5

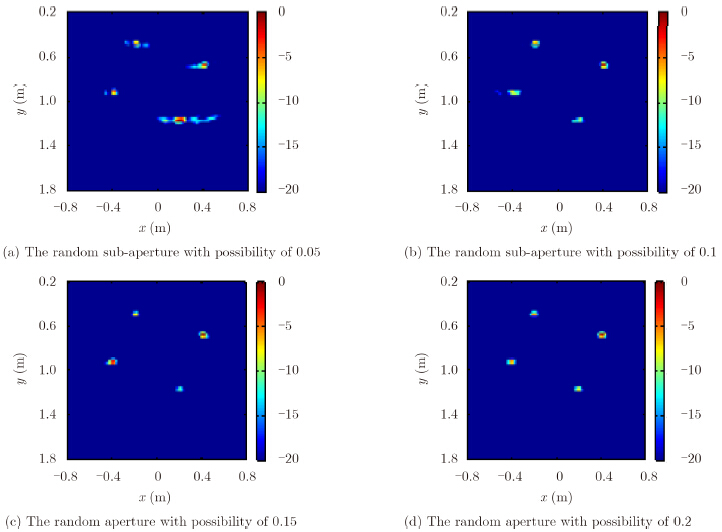Fig. 5  Results with different setup of random sub-apertures

Comparing the reconstructed images by traditional method with our method, it is clear that our method can suppress the multipath ghosts noteworthy and enhance the real targets at the same time. To avoid interpretation errors, the normalized mean square error (MSE)^[22] was calculated to characterize how the reconstructed images compared to the true object. The normalized mean square error for all pixels is defined as:

where ${{x}_{i}}$ is the true value at the object pixel i and ${{\hat{x}}_{i}}$ is the reconstructed value for that pixel. In order to make a fair comparison to the binary object measured, we implemented a binary threshold value in which all values at or below this were treated as a binary 0 and all above were treated as a binary 1. Considering the relationship of real targets and ghosts, the threshold value is chosen to be 0.01 in this paper. The MSEs of images reconstructed by different methods are listed in Tab. 1. The MSEs of images reconstructed by sub-aperture and random aperture method are evidently smaller than the traditional method. It seems that it is hard to say which method is better between sub-aperture method and random aperture method because their MSEs are almost the same. But the sub-aperture method lost a target as shown in Fig. 3(h) while the random aperture method can reconstruct all the targets. So we can say that the random aperture method can be used to address the multipath ghost and it is better than traditional method and sub-aperture method.

Tab. 1

Tab. 1   MSEs of images reconstructed by different methods Method Traditional Sub-aperture Random aperture p=0.05 p=0.1 p=0.15 p=0.2 MSE (%) 42.1 4.39 5.32 4.56 4.39 4.31

Tab. 1   MSEs of images reconstructed by different methods

This subsection consider the scene of through-wall imaging, as illustrated in Fig. 1(b), where the target and antenna are located at different sides of the wall. The thickness and relative dielectric constant of the wall are specified to be 0.3 m and 6.0 respectively. The complete measurement line is at the distance of 0.1 m away from the wall. Other simulation parameters are the same as above. Note that here the Green's function is for three-layered medium, in contrast to the two-layered medium for GPR imaging.

Analogously, the image obtained by using the whole measurement aperture is shown in Fig. 6, which shows that four targets are severely disturbed by the clutter of false targets, and it is pretty a risk in distinguishing real targets from false targets. The final images obtained by random sub-apertures with different probability of random apertures are shown in Fig. 7. From these simulations, it can be observed that the ghosts can be significantly impaired by using proposed methodology, and the real targets can be enhanced at same time.

Fig. 6

Fig. 6  Reconstruction with the whole measurement aperture

Fig. 7

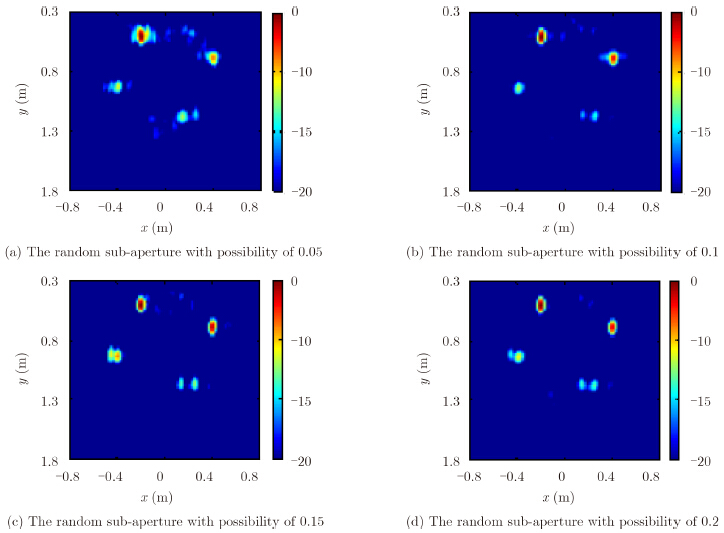Fig. 7  Reconstruction results with the random sub-apertures

This letter presents a novel probabilistic concept of suppressing the multipath ghosts involved in the problem of GPR and TWI imaging. First, this letter provides a model of the reflectivity of probed objects in a probability function. Second, the concept of the random sub-aperture is incorporated into the imaging procedure. Thus, the final radar image is regarded as the joint probability distribution, which is the product of retrieved radar images corresponding to multiple random sub-apertures. Finally, a selected number of numerical experiments is provided to demonstrate the performance of proposed imaging methodology for the application of GPR and TWI imaging.