1 引言
线阵3维SAR是一种典型的阵列SAR,其基本原理是在运动平台上垂直于运动方向放置1个线性阵列天线,通过平台运动合成虚拟面阵天线获得面阵平面内的2维分辨率,并结合脉冲压缩技术获得雷达视线方向高分辨率,从而实现对观测场景的3维成像[1, 2]。线阵3维SAR成像的难点在于飞行平台限制了切航迹向阵列长度,导致了切航迹向分辨率往往较差。同时,沿航迹向的分辨率受合成孔径长度制约也难以提高。
目前,用现代谱估计方法取代傅里叶变换提高成像分辨率已经成为雷达成像领域研究的热点。旋转不变子空间(Estimation of Sgnal Parameters by Rotational Invariance Technique,ESPRIT)算法最早是由Roy,Paulath和Kailath提出[3],含义是利用旋转不变子空间估计信号参数。近年来,ESPRIT算法在雷达成像领域已得到广泛的应用。文献[4]将Unitary ESPRIT算法用于2维SAR成像,说明了ESPRIT算法性能优于FFT,但是算法的复杂度和运算量大幅增加,难以满足实时性的要求。文献[5]在ISAR成像中证明了酉ESPRIT算法具有更优的分辨率和抗噪性能,但只在方位维实现了超分辨,没有扩展到距离向。而文献[6]虽然用ESPRIT算法实现了2维ISAR超分辨成像,但是2维位置幅度估计和配对问题均采用最小二乘方法,在点目标个数未知的情况下,会遗漏散射系数较小的目标,同时增加了运算量。文献[7]采用2维MUSIC超分辨算法替代FFT实现了SAR成像,降低了旁瓣的影响,但对距离向和方位向都进行协方差运算和最小二乘估计,运算量大大增加。由于3维空间大量区域不包括散射点,在下视模式下同一等高面只存在少量的目标点,因此点目标在3维场景中可视为稀疏的。将上述超分辨算法用于3维场景后仍存在点目标个数难以准确估算、2维ESPRIT算法计算量大等问题,因此本文基于多输入多输出(Multiple Input Multiple Output,MIMO)线阵3维SAR成像模型,提出了一种用于线阵3维SAR成像的2维快速ESPRIT算法。它的特点是:一是将传统的1维ESPRIT算法扩展到了2维。传统的扩展方法是采用2维ESPRIT算法进行位置估计,其运算量是1维ESPRIT算法的平方倍,运算速度非常慢,而本文则采用L型搜索替代平面搜索进行位置估计,可以大幅降低运算量并提高运算速度,同时对切航迹向和沿航迹向进行超分辨成像。二是采用盖式圆方法[8]准确获得点目标个数。三是提出了基于“区域生长”的位置配对方法,结合RD算法的成像结果快速求出目标散射系数完成成像,避免使用最小二乘方法重新计算。实验结果表明,本文所提出的2维快速ESPRIT算法与传统成像算法相比,成像分辨率明显提高、旁瓣电平显著降低;且与面阵2维ESPRIT算法相比,运算量和复杂度大幅降低。
本文结构安排如下:第1节介绍基于MIMO线阵的3维SAR成像模型;第2节提出用于线阵3维SAR成像的2维快速ESPRIT算法;第3节是仿真实验。
2 基于MIMO线阵的3维SAR成像模型
基于MIMO线阵的3维SAR成像几何模型如图 1所示工作于下视模式,采用多发多收的阵列结构,其中,高度向是雷达波束照射方向,沿航迹向是载机的航行方向,切航迹向是机翼方向。
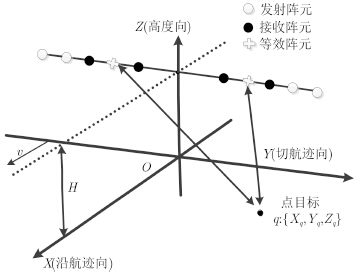 | 图 1 基于MIMO线阵的3维SAR成像几何模型 Fig. 1 Linear array SAR imaging model based on MIMO |
假设机翼上方向上安置N个发射阵元,排布于机翼两侧,间隔为2d,M个接收阵元,中心在原点且均匀分布,间隔为Nd,距离原点最远的接收阵元距离最近的发射阵元间隔为d。其基于相位中心近似(Phase Center Approximation,PCA)原理[9]的等效阵列为均匀分布的收发共用T/R的线阵,阵列中心位于原点,阵元数为NM,间隔为d。载机飞行高度为H,沿X轴以速度v飞行,发射信号的中心频率是f0。
高频激励下,目标可采用Swerling模型,解调后的回波信号可表示为:
| $\begin{array}{*{20}{r}} {W\left( {t,u} \right) = \sum\limits_{q = 1}^Q {{\varsigma _q}\;{\rm{rect}}\left( {\frac{{t - {t_{nq}}\left( u \right)}}{{{T_{\rm{p}}}}}} \right)} }\\ { \cdot \exp \left\{ {{\rm{j}}\pi {K_{\rm{r}}}{{\left( {t - {t_{nq}}} \right)}^2}} \right\}}\\ { \cdot \exp \left\{ { - {\rm{j}}\frac{{4\pi {f_{0}}{r_{nq}}\left( u \right)}}{{\rm{c}}}} \right\}} \end{array}$ | (1) |
| $\begin{aligned} {r_{{nq}}}\left( u \right) = & \Big( {{\left( {{x_n}\left( u \right) - {x_{\! q}}} \right)}^2} + {{\left( {{y_n}\left( u \right) - {y_q}} \right)}^2} \\ & + {{\left( {{z_n}\left( u \right) - {z_q}} \right)}^2} \Big) ^{1/2} \end{aligned}$ | (2) |
| ${r_{{nq}}}\left( u \right) \approx {r_0} + \frac{{{{\left( {uv - {x_{\! q}}} \right)}^2}}}{{2{r_0}}} + \frac{{{y_n^2} - 2{y_n}{y_q}}}{{2{r_0}}}$ | (3) |
PCA产生的误差相位为:
| $dr\left( i \right) \! = \! {r_{\text{s}}}\left( i \right) \! + \! {r_{\text{r}}}\left( i \right) \! - \! 2{r_{nq}}\left( i \right),i \! = \! 1,2,\cdots ,NM$ | (4) |
由图 1可知,线阵3维SAR与传统2维SAR的区别是在机翼方向上布置了N + M个阵元。在成像处理方面,3维RD算法是对每个阵元的回波进行高度向和沿航迹向的压缩处理,然后将等效NM个回波信号叠加进行切航迹向聚焦[10]。各个方向上的压缩过程都是与匹配函数相乘滤波的过程[11]。切航迹向完成聚焦后,在距离多普勒域中的信号为:
| $\begin{array}{*{20}{c}} {{S_{{\rm{ac}}}}\left( {t,{f_{u}}} \right) = {\varsigma _q}\;{{\mathop{\rm p}\nolimits} _{\rm{r}}}\left( {t - {t^\prime }} \right){{\mathop{\rm p}\nolimits} _{\rm{a}}}\left( {{f_{u}} - f_{u}^\prime } \right)}\\ { \cdot \exp \left( { - {\rm{j}}\frac{{4\pi {f_{0}}{r_0}}}{{\rm{c}}} + {\rm{j}}\frac{{4\pi {f_{0}}{y_n}{y_q}}}{{{\rm{c}}{r_0}}} - {\rm{j}}\frac{{2\pi f{_u}{x_{q}}}}{v}} \right)} \end{array}$ | (5) |
| $\begin{array}{*{20}{c}} {{S_{{\rm{cc}}}}\left( {t,u,\theta } \right) = {\varsigma _q}\;{{\rm{p}}_{\rm{r}}}\left( {t - {t^\prime }} \right){{\rm{p}}_{\rm{a}}}\left( {u - {u^\prime }} \right)}\\ { \cdot {{\rm{p}}_{\rm{x}}}\left( {\sin \theta - \sin {\theta _0}} \right)\exp \left( { - {\rm{j}}\frac{{4\pi {f_{0}}{r_0}}}{{\rm{c}}}} \right)} \end{array}$ | (6) |
根据SAR理论及分辨率的定义,线阵3维SAR各方向上的分辨率为[1]:
| $\left\{ {\begin{array}{*{20}{c}} \!\! {{\rho _{\text{x}}} = \frac{{\lambda H}}{{2{L_{\text{s}}}}}} \\ \!\! {{\rho _{\text{y}}} = \frac{{\lambda H}}{{2{L_{\text{a}}}}}} \\ \!\! {{\rho _{\text{z}}} = \frac{\rm c}{{2B}}} \end{array}} \right.$ | (7) |
3 2维快速ESPRIT算法
本文提出的2维快速ESPRIT算法主要通过以下几个步骤完成:
(1)为了得到ESPRIT算法矩阵分解时奇异值的个数,结合线阵3维SAR成像模型,采用盖式圆方法估计点目标数量。
(2)为了降低运算量,对传统的2维ESPRIT算法进行改进,用L型搜索替代平面搜索,即在切航迹向和沿航迹向分别选择1行阵列估计2维位置。
(3)采用2维快速ESPRIT算法求出的2维位置不是一一对应的,会在平面内出现多种排列组合的情况,形成虚假目标。为了消除虚警,本文提出了基于“区域生长”的位置配对新方法,将配对的位置代入RD算法成像结果得到目标散射系数,相比于最小二乘估计,减少了运算量且降低了旁瓣的影响。
3.1 2维快速ESPRIT算法
盖式圆方法是信源估计中常用的一种方法,在低噪声的情况下,性能优于其它估计算法[8]。考虑到点目标个数是确定ESPRIT算法过程中奇异值数量的关键,因此根据线阵3维SAR成像模型,采用盖式圆方法估计点目标个数。
盖式圆利用Gerschgorin圆盘定理[7],首先取式(5)中切航迹向聚焦后单个距离切面上的任意一行数据,这NM个数据沿航迹向频率相同,其中nr,na表示高度向和沿航迹向的任一采样点,Nx = NM表示等效阵元个数。
| $\begin{array}{*{20}{c}} {X = \left[ {{S_{{\rm{ac}}}}\left( {{n_{\rm{r}}},{n_{\rm{a}}},1} \right),{S_{{\rm{ac}}}}\left( {{n_{\rm{r}}},{n_{\rm{a}}},2} \right), \cdots ,} \right.}\\ {{{\left. {{S_{{\rm{ac}}}}\left( {{n_{\rm{r}}},{n_{\rm{a}}},{N_{\rm{x}}}} \right)} \right]}^{\rm{T}}}} \end{array}$ | (8) |
然后求出切航迹向信号X的协方差矩阵R,并分块成如下形式:
| $R = {\left[ {\begin{array}{*{20}{c}} {{R_0}' }&r\\ {{r^H}}&{{r_0}} \end{array}} \right]_{{N_{\rm{x}}} \times {N_{\rm{x}}}}}$ | (9) |
| ${R_{\rm{U}}} = {\left[ {\begin{array}{*{20}{c}} {{\lambda ^\prime }}&0& \cdots &{{\rho _1}}\\ 0&{{\lambda ^\prime }}& \cdots &{{\rho _2}}\\ \vdots & \vdots & \ddots & \vdots \\ {\rho _1^*}&{\rho _2^*}& \ldots &{{r_{{N_{\rm{x}}}{N_{\rm{x}}}}}} \end{array}} \right]_{{N_{\rm{x}}} \times {N_{\rm{x}}}}}$ | (10) |
式(10)中,$\lambda '$表示Nx – 1个阵元信号特征矢量对应的特征值。根据盖式圆理论,点目标信号对应的半径ri = |${\rho _i}$|较大,而噪声对应的盖式半径ri ≈ 0,因此,采用盖式圆盘估计法作为计算点目标的准则[6]:
| ${\text{GDE}}\left( k \right) = {r_k} - \frac{{D\left( L \right)}}{{{N_{\text{x}}} - 1}}\sum\limits_{i = 1}^{{N_{\text{x}}} - 1} {{r_i}} > 0$ | (11) |
3.2 ESPRIT算法估计2维位置
线阵3维SAR的切航迹向是对阵元进行等间隔的空间采样,而沿航迹向是等间隔的时间采样,采样点可视为虚拟阵元,如图 2所示。因此,切航迹向和沿航迹向形成了2维虚拟面阵。传统2维ESPRIT算法对面阵内所有阵元同时进行处理,计算量是1维ESPRIT的平方倍[12, 13],计算速度非常慢。本文为了提高运算速度,提出2维快速ESPRIT算法,选取切航迹向和沿航迹向的 L型阵列进行位置估计 。
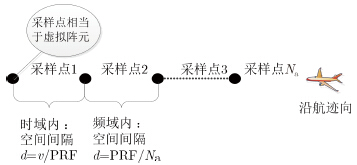 | 图 2 沿航迹向虚拟阵列示意图 Fig. 2 Illustration of the virtual array in along-track direction |
ESPRIT算法利用子阵结构的旋转不变性估计信号参数,适用于两个完全相同的子阵,并且这两个子阵具有已知的间隔[8]。本文首先选取切航迹向的阵列作为子阵,切航迹向聚焦后的式(8)的值作为接收矢量X;将X循环移动单位距离d作为另一个接收矢量Y。因此,接收矢量表示为:
| $X = AS + {N_{\rm{1}}}$ | (12) |
| $Y = A\Phi S + {N_{\rm{2}}}$ | (13) |
| $A = {\left[{a\left( {{\theta _1}} \right),a\left( {{\theta _2}} \right),\cdots ,a\left( {{\theta _q}} \right)} \right]_{NM \times q}}$ | (14) |
| $a\left( {{\theta _i}} \right) = \left[{\exp \left( {{\rm{j}}\frac{{4\pi {f_{0}}{y_1}{y_i}}}{{{\rm{c}}{r_0}}}} \right),\cdots ,} \right.{\left. {\exp \left( {{\rm{j}}\frac{{4\pi {f_{0}}{y_{NM}}{y_i}}}{{{\rm{c}}{r_0}}}} \right)} \right]^{\rm{T}}}$ |
根据式(12)和式(13),求得接收数据的协方差矩阵为:
| ${\begin{array}{*{20}{l}} {{R_{XX}} = {\rm{E}}\left( {X{X^{\rm{H}}}} \right) = A{\rm{E}}\left( {S{S^{\rm{H}}}} \right){A^{\rm{H}}} + {\sigma ^2}I}\\ {{R_{XY}} = {\rm{E}}\left( {X{Y^{\rm{H}}}} \right) = A{\rm{E}}\left( {S{S^{\rm{H}}}} \right){\Phi ^{\rm{H}}}{A^{\rm{H}}} + {\sigma ^2}Z} \end{array}}$ | (15) |
| $Z = {\left[ {\begin{array}{*{20}{c}} 0&0& \cdots &0\\ 1&0& \cdots &0\\ 0&{}& \cdots &{}\\ 0&0& \cdots &0 \end{array}} \right]_{{N_{\rm{x}}} \times {N_{\rm{x}}}}}$ | (16) |
为了消除成像过程中噪声的影响,定义${C_{XX}}$和${C_{XY}}$如下:
| $\left\{ {\begin{array}{*{20}{c}} {{C_{XX}} = {R_{XX}} - {\sigma ^2}I}\\ {{C_{XY}} = {R_{XY}} - {\sigma ^2}Z} \end{array}} \right.$ | (17) |
在点目标不相干的情况下,去噪后的${C_{XX}}$和${C_{XY}}$矩阵是满秩的。但是当点目标相干时,由于${C_{XX}}$和${C_{XY}}$非满秩,存在相交的零子空间,导致$A\alpha = \lambda B\alpha \equiv 0$,即l可以取任意值,因此广义特征值的求解会出现病态解。对于线阵3维SAR系统而言,点目标之间一般具有相关性,因此需要对传统ESPRIT算法进行改进。
本文采用TLS-拓广ESPRIT算法[16, 17],将${C_{XX}}$的特征值分解为如下形式:
| $\begin{array}{*{20}{c}} {{C_{XX}} = U\Sigma {V^H}}\\ { = \left[ {{U_1}{U_2}} \right]\left[ {\begin{array}{*{20}{c}} {{\Sigma _1}}&0\\ 0&{{\Sigma _2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {V_1^H}\\ {V_2^H} \end{array}} \right]} \end{array}$ | (18) |
式(18)中,${\Sigma _1}$是q×q矩阵,此时${C_{XX}}$和${C_{XY}}$的广义特征值就是$\left\{ {{\Sigma _1},U_{1}^{\rm{H}}{C_{XY}}{V_{\rm{1}}}} \right\}$的广义特征值$\lambda (i),(i = 1,2,\cdots ,q)$,根据得到的相位值$\phi = \left( {\frac{{4\pi d{y_q}}}{{\lambda {r_0}}}} \right)$反推出yq的值,从而完成切航迹向的位置估计。
沿航迹向的估计与切航迹向上估计方法类似,首先任取沿航迹向的一列虚拟阵元同切航迹向的阵列构成L型阵列结构,选择聚焦后的式(5)中单个距离切面上的任意一列数据,这Na个数据的切航迹向阵元位置相同,其中nr,nx表示高度向和切航迹向的任一采样点。式(12)中的接收矢量X表示为:
| $X = {[{S_{{\rm{ac}}}}\left( {{n_{\rm{r}}},1,{n_{\rm{x}}}} \right),{S_{{\rm{ac}}}}\left( {{n_{\rm{r}}},2,{n_{\rm{x}}}} \right), \cdots ,\;{S_{{\rm{ac}}}}\left( {{n_{\rm{r}}},{N_{\rm{a}}},{n_{\rm{x}}}} \right)]^{\rm{T}}}$ | (19) |
沿航迹向的协方差矩阵${{\rm{R}}_{{\rm{XX}}}}$和${{\rm{R}}_{XY}}$与式(15)的选取方法相同,旋转矢量式(13)中$u = - \frac{{2\pi {f_{u}}{x_{q}}}}{v}$。最后由广义特征值$\lambda (i),i = 1,2,\cdots {\rm{,q}}$求出相位,通过$\phi = - \frac{{2\pi d{x_{q}}}}{v}$反推出沿航迹向位置xq的值,就得到点目标的2维位置估计值。
3.3基于区域生长的点目标2维位置配对方法
上节通过本文提出的2维快速ESPRIT算法分别完成了切航迹向和沿航迹向的位置估计,但是由于无法确定目标位置的一一对应关系,会出现许多虚警目标,如图 3所示。本文结合“区域生长”的规则,提出新的配对方法消除虚警目标,求得点目标的精确位置。
 | 图 3 2个点目标2维位置示意图 Fig. 3 Illustration of two-dimensional positions of three scatterers |
为了得到切航迹向和沿航迹向的2维位置对应关系,首先要消除高度向的影响。将RD算法最终成像结果${S_{cc}}(t,u,\theta )$按照高度向进行求和,得到关于切航迹向和沿航迹向的2维矩阵${S_{{\rm{rx}}}}{\left( {i,j} \right)_{{N_{\rm{a}}} \times {N_{\rm{x}}}}} $。
${S_{{\rm{rx}}}}{\left( {i,j} \right)_{{N_{\rm{a}}} \times {N_{\rm{x}}}}} $相当于多个2维SAR成像结果的叠加,会产生更明显的旁瓣。当点目标的间隔距离小于分辨率时,相邻目标点的旁瓣叠加在一起,严重干扰对目标位置的判断,甚至会掩盖某些目标点的存在。由RD算法沿航迹向点扩展函数图 4可看出,两个相邻点目标之间一定存在一个凹点,这个凹点就是两个点目标聚焦值的平衡点。在平衡点的两侧,两个点目标的幅值各自占主导地位,即目标的散射中心一定分别位于这两个区域内。
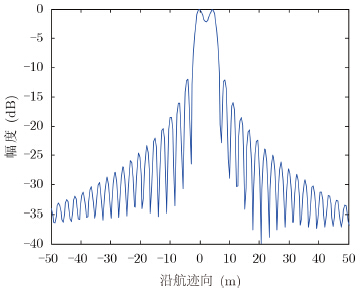 | 图 4 沿航迹向点扩展函数示意图 Fig. 4 Illustration of PSF in cross-track direction |
基于上述平衡点的理论,本文提出一种新的配对方法,以3维RD成像结果${S_{{\rm{rx}}}}{\left( {i,j} \right)_{{N_{\rm{a}}} \times {N_{\rm{x}}}}} $为基础,以图像处理中“区域生长”的思想为主线,选择切航迹向和沿航迹向的2维平面,从极大值点出发,逐渐合并区域找到所有局部极大值点,估计出点目标的大概位置,再将由ESPRIT算法得到的2维位置逼近这些位置进行配对,最后将精确位置代入RD算法结果中估计点目标散射系数。
本文提出的基于“区域生长”的配对算法具体步骤如下:
(1)“生长区域”[18]:定义一个新矩阵$S{1_{{\rm{rx}}}}{\left( {i,j} \right)_{{N_{\rm{a}}} \times {N_{\rm{x}}}}} = {S_{{\rm{rx}}}}{\left( {i,j} \right)_{{N_{\rm{a}}} \times {N_{\rm{x}}}}}$,将RD算法成像结果的2维累加矩阵作为区域生长的“原图像”。设变量i表示点目标个数,即需要搜索的局部极值点个数,并置初值为零。
(2)“种子点”:遍历S1rx找出极大值,作为区域生长的“种子点”,将它在矩阵中的位置存于maq×q,设记录生长次数的变量k=0。
(3)“生长规则”:对种子点的四连通区域进行遍历,此时种子点取原矩阵S1rx中对应位置上的值。若遍历值比种子点的值大,此时种子点就是平衡点,停止此方向上的遍历,并将S1rx中种子点的值置零;若相反,则将此遍历点作为新的种子点重复进行此步骤,将原种子点和遍历点在S1rx中的值置零,并设k=k+1。
(4)“终止条件”:k<a是第3步的“终止条件”,a是个常数,作为遍历区域的半边长。第3步终止时,i=i+1,并跳到第2步继续进行,i<q作为整个算法的“终止条件”,q是点目标的个数。
上述提出的“区域生长”配对算法可以粗略得到由RD算法得到的目标2维位置,但是这个位置是在式(7)的分辨率条件下完成的,会出现较大的误差。根据上文平衡点的理论可知,2维快速ESPRIT算法估计出的位置大小顺序与RD算法是一致的。因此,根据ma存储的值将RD算法求出的位置进行大小排序,并按照此顺序将2维快速ESPRIT算法得到的位置进行配对,就可求出目标的精确位置。
传统的ESPRIT超分辨算法主要分两步,首先估计点目标的位置,然后采用最小二乘方法估计出目标散射系数完成成像:
| $\mathop S\limits^ \wedge = \left( {{A^H}{A^{ - 1}}{A^{\rm{H}}}X} \right)$ | (20) |
但式(20)中导向矢量A的值要根据式(14)重新计算,运算量大且过程复杂。本文采用RD算法与超分辨方法结合的方式,将配对后的点目标2维精确位置直接代入到RD算法的成像结果中,就能快速求出目标的散射系数。
本文提出的用于线阵3维SAR的2维快速ESPRIT算法流程如图 5所示。
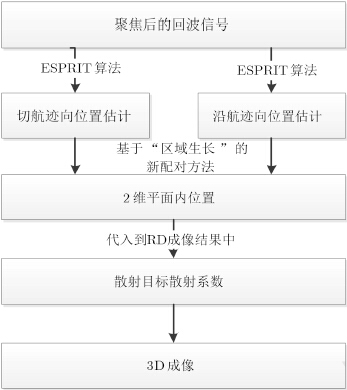 | 图 5 用于线阵3维SAR成像的2维快速ESPRIT算法处理流程 Fig. 5 Flow of the proposed algorithm |
4 实验结果与分析 4.1 多个点目标成像
为了验证本文提出的2维快速ESPRIT算法的性能,利用点目标仿真实验进行分析。仿真参数如表 1所示。
| 表 1 实验仿真参数 Tab. 1 Simulation parameters |
由式(7)求得切航迹向和沿航迹向理论分辨率分别为${\rho _{\rm{x}}} = 1.875 \ {\rm{m}},\ {\rho _{\rm{a}}} = 1 \ {\rm{m}}$。ESPRIT算法能突破瑞丽极限的限制,区分出间隔小于分辨率的点目标。如图 6所示,2维ESPRIT算法得到所有点目标的精确位置。
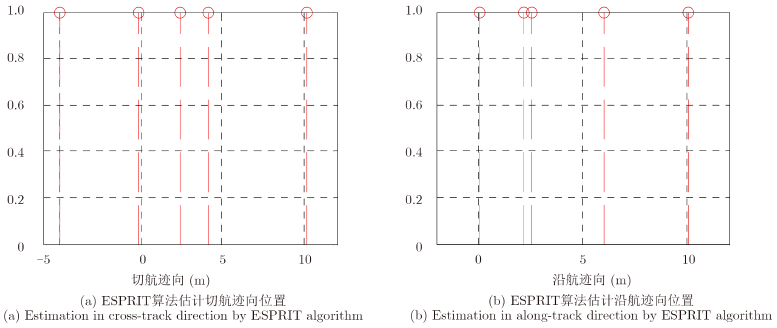 | 图 6 ESPRIT算法估计出的2维位置 Fig. 6 Estimation in cross and along-track directions by ESPRIT algorithm |
图 7分别给出了RD算法和本文方法求得的切航迹向和沿航迹向2维成像结果。相比于RD算法,本文算法不仅大大降低了旁瓣的影响,而且区分出了2和3号点目标。图 8给出了相应的3维成像结果。
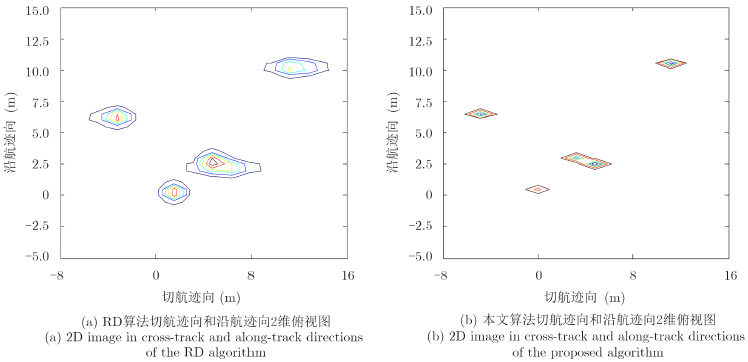 | 图 7 RD算法和本文算法2维俯视对比图 Fig. 7 Comparison of 2D image between RD algorithm and proposed algorithm |
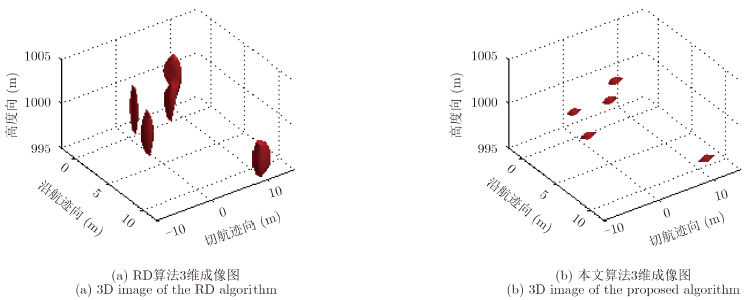 | 图 8 RD算法和本文算法3维成像对比 Fig. 8 Comparison of 3D image between RD algorithm and proposed algorithm |
为了研究SNR对两个方向上分辨率的影响,将点目标的切航迹向位置间隔从$0.4{\rho _{\rm{x}}}$增加到${\rho _{\rm{x}}}$,沿航迹向的位置从$0.4{\rho _{\rm{a}}}$增加到${\rho _{\rm{a}}}$,目标在不同SNR下的可分辨概率表示在图 9中,其中蒙特卡洛仿真次数为500。从图 9中可以看出,本文提出的算法突破了传统分辨率的限制,SNR的值越大,点目标之间的距离越大,系统的分辨性能越好。同时,在噪声影响较大的情况下,系统的分辨性能会受到较大的影响,达不到预先的要求,此时综合运算时间和分辨率的影响,应在RD算法和本文算法的选择上进行权衡。
 | 图 9 不同SNR下2维可分辨概率 Fig. 9 Probability of resolution versus the SNR in cross and along-track directions |
4.2 不同散射系数的目标点成像
按照4.1节实验中的场景参数,选取目标点1和4,将目标点1的散射系数设为1.0,目标点4的散射系数设为0.5。图 10分别给出了RD算法和本文算法得到的切航迹向和沿航迹向2维成像结果。本文算法在降低旁瓣的同时,也可得到点目标散射系数。
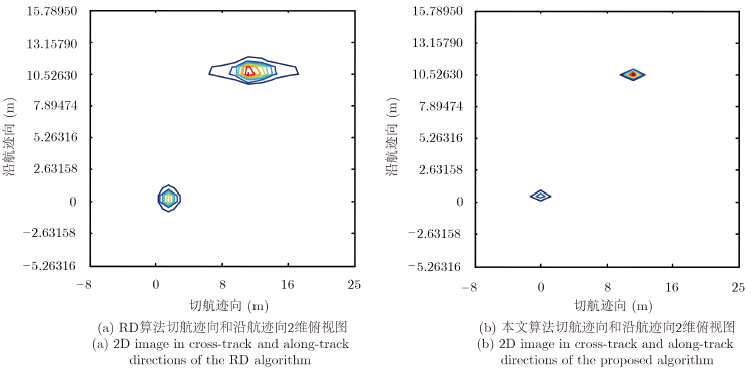 | 图 10 RD算法和本文算法2维俯视对比图 Fig. 10 Comparison of 2D image between RD algorithm and proposed algorithm |
从上述实验结果可以看出,本文提出的用于线阵3维SAR成像的2维快速ESPRIT算法位置估计精度远高于RD算法。在成像效果方面,不仅大幅提高了切航迹向和沿航迹向的分辨率,而且降低了旁瓣电平的影响。在噪声影响较小的情况下可以获得良好的分辨性能。
5 结论
针对线阵3维SAR系统切航迹向和沿航迹向分辨率难以提高的问题,本文阐述了一种用于线阵3维SAR的2维快速ESPRIT超分辨成像算法。该算法适用于各种收发形式的等距阵列模型,在提高2维分辨率和成像质量的同时,降低了运算量和处理时间。但在实际的线阵3维SAR系统中噪声影响较大,这会对该算法的性能造成影响。下一步工作中将优化算法的鲁棒性并提高其适应性,精简运算步骤以进一步降低运算时间,推动线阵3维SAR的实用化进程。
| [1] | 王斌, 王彦平, 洪文, 等. 线阵SAR三维成像分辨率分析[J]. 计算机仿真, 2011, 28(3): 282-286. Wang Bin, Wang Yan-ping, Hong Wen, et al. Analysis of resolution for SAR 3D imaging using linear array antennas[J]. Computer Simulation, 2011, 28(3): 282-286.(  2) 2) |
| [2] | 成晨. 三维合成孔径雷达超分辨成像方法研究[D]. [硕士论文], 电子科技大学, 2012. Cheng Chen. 3D SAR superresolution imaging algorithms[D]. [Master dissertation], University of Electronic Science and Technology of China, 2012.(  1) 1) |
| [3] | Colin Haley. Talk about ESPRIT[J]. Electronic and Power, 1986, 32(5): 377-380.( 1) 1) |
| [4] | Zhang Ping, Li Zhen, and Chen Quan. 2D UESPRIT superresolution SAR imaging algorithm[C]. Geoscience and Remote Sensing Symposium, Honolulu, 2010: 4067-4070.( 1) 1) |
| [5] | 冯德军, 王雪松, 陈志杰, 等. 酉ESPRIT超分辨ISAR成像方法[J]. 电子学报, 2005, 33(12): 2097-2100. Feng De-jun, Wang Xue-song, Chen Zhi-jie, et al. Super-resolution ISAR imaging using unitary ESPRIT[J]. Acta Electronica Sinica, 2005, 33(12): 2097-2100.(  1) 1) |
| [6] | 焦芸, 田野, 宿富林. 基于一种二维ESPRIT算法的ISAR超分辨成像[J]. 哈尔滨师范大学自然科学学报, 2005, 21(4): 35-38. Jiao Yun, Tian Ye, and Su Fu-lin. ISAR super-resolution imaging based on a 2-D ESPRIT algorithm[J]. Natural Science Journal of Harbin Normal University, 2015, 21(4): 35-38.(  2) 2) |
| [7] | 张平, 商建, 杨汝良. 一种有效的二维MUSIC超分辨SAR成像算法[J]. 系统仿真学报, 2010, 22(1): 184-187. Zhang Ping, Shang Jian, and Yang Ru-liang. Efficient 2D MUSIC superresolution SAR imaging method[J]. Journal of System Simulation, 2010, 22(1): 184-187.(  2) 2) |
| [8] | 张小飞, 汪飞, 徐大专. 阵列信号处理的理论和应用[M]. 北京: 国防工业出版社, 2010: 31-33. Zhang Xiao-fei, Wang Fei, and Xu Da-zhuan. The Theory and Application of Array Signal Processing[M]. Beijing: National Defense Industry Press, 2010: 31-33.(  4) 4) |
| [9] | 朱宇涛. 多通道ISAR成像技术研究[D]. [博士论文], 国防科学技术大学, 2011. Zhu Yu-tao. Multiple-channel ISAR imaging[D]. [Ph.D. dissertation], National University of Defense Technology, 2011.(  2) 2) |
| [10] | 于春艳, 谢亚楠, 赵海兰, 等. 基于新型阵列配置的机载MIMO-SAR下视三维成像性能研究[J]. 电子测量技术, 2014, 37(2): 64-69. Yu Chun-yan, Xie Ya-nan, Zhao Hai-lan, et al. Airborne downward-looking MIMO 3D-SAR imaging properties based on the new array configuration[J]. Electronic Measurement Technology, 2014, 37(2): 64-69.(  2) 2) |
| [11] | Wang Wei, Wu Wei-hua, Su Wu-ge, et al. High squint mode SAR imaging using modified RD algorithm[C]. 2013 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Beijing, 2013: 589-592.( 1) 1) |
| [12] | Hu An-zhong, Lv Tie-jun, Gao Hui, et al. An ESPRIT-based approach for 2-D localization of incoherently distributed sources in massive MIMO systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 996-1011.( 1) 1) |
| [13] | Li Jian-feng and Zhang Xiao-fei. Unitary reduced-dimensional estimation of signal parameters via rotational invariance techniques for angle estimation in monostatic multiple-input-multiple-output radar with rectangular arrays[J]. IET Radar, Sonar and Navigation, 2013, 8(6): 575-584.( 1) 1) |
| [14] | Ahmed A, Khan M F, and Tufail M. Multiple Invariance Cumulant ESPRIT for DOA Estimation[C]. 2014 International Conference on Robotics and Emerging Allied Technologies Engineering, Pakistan, 2014: 157-159.( 1) 1) |
| [15] | Fayad Y, Wang Cai-yun, Hafez A E D S, et al. Direction of arrival estimation using novel ESPRIT method for localization and tracking radar systems[C]. Proceedings of 2014 11th International Bhurban Conference on Applied Sciences & Technology (IBCAST), Islamabad, Pakistan, 2014: 396-398.( 1) 1) |
| [16] | 张东浩. 线阵三维SAR成像算法研究及仿真[D]. [硕士论文], 电子科技大学, 2010. Zhang Dong-hao. Analysis and simulation of LASAR imaging[D]. [Master dissertation], University of Electronic Science and Technology of China, 2010.(  2) 2) |
| [17] | Qu Le-le, Sun Qiang, Yang Tian-hong, et al. Time-delay estimation for ground penetrating radar using ESPRIT with improved spatial smoothing technique[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 11(8): 1315-1319.( 1) 1) |
| [18] | Puneet Jain. An adaptive single seed based region growing algorithm for color image segmentation[C]. India Conference (INDICON), Mumbai, 2013: 1-6.( 1) 1) |


