②微波成像技术国家重点实验室 北京 100190
③中国科学院大学 北京 100049
②National Key Laboratory of Microwave Imaging Technology, Beijing 100190, China
③University of Chinese Academy of Sciences, Beijing 100049, China
圆迹合成孔径雷达(Circular Synthetic Aperture Radar,CSAR)是20世纪90年代提出的一种SAR工作模式[1],它通过雷达随平台做360°圆周运动,并将波束中心始终指向场景中心作为成像几何[2]。传统条带SAR模式在方位向利用平台的直线飞行形成虚拟线阵,在距离向发射宽带信号以获得2维斜距平面图像。而圆迹SAR通过平台的曲线运动形成2维面阵,结合脉冲压缩技术能够实现对目标的3维观测。它能够有效拓宽波数域带宽,2维平面理论分辨率达亚波长量级[3]。相比条带SAR单一的侧视成像几何,圆迹SAR对目标进行360°全方位观测可有效消除条带SAR引起的叠掩、透视收缩和阴影等现象[4]。利用全方位观测的互补性,圆迹SAR可获取目标在各个方向的散射特征,实现场景目标的精细特征描述。因此,基于这些独特优势,圆迹SAR在高精度测绘、灾害评估等方面展现了应用潜力,近年来越来越得到国内外学者的关注[5, 6]。
目前,国内外研究机构已多次开展机载圆迹SAR试验,获取了多个不同波段不同极化的图像。2004年瑞典国防研究院(FOI)基于CARABAS-Ⅱ系统获取了森林地区的VHF波段圆迹SAR图像,证实了圆迹SAR对检测隐藏目标的潜力[7, 8]。2008年美国空军研究实验室(AFRL)开展了名为“GOTCHA”[9]的X波段多航过机载圆迹SAR试验,对车辆进行了3维重建和轮廓估计[10]。2009年德国宇航中心(DLR)通过E-SAR系统获取了Kaufbeuren地区L波段全极化360°高分辨图像,并对场景中的树木和建筑进行了3维成像[11]。中科院电子所[12, 13]于2011年开展了国内首次机载圆迹SAR飞行试验,成功获取了P波段全极化机载圆迹SAR图像。通过这些试验,圆迹SAR展示了常规条带成像机制不具备的独特优势,为获取更丰富精细目标信息的提供了新的观测途径和技术手段[14, 15]。
由于圆迹SAR成像时已包含基于运动测量数据的补偿,因此高分辨率圆迹SAR图像的获取主要受到导航系统精度的制约。实现高质量圆迹SAR图像,通常要求轨迹测量误差控制在波长的1/16。一方面波段越高,对导航系统要求也越高;另一方面圆迹SAR合成孔径时间较长,导航系统难以保持较好的稳定性,同时平台的圆周运动使惯性器件输出数据的解算误差随着时间累积而增大,影响天线相位中心的定位精度。目前国内外虽已开展过高波段(X)机载试验,但获得全方位大场景机载圆迹SAR图像的试验采用的波段均较低(P和L波段)。因此在导航系统精度受限的情况下,运动补偿方法的研究成为影响圆迹SAR图像质量的关键因素之一。文献[16]通过场景中布放的角反射器组,基于脉冲压缩域回波的强脉冲响应跟踪角反射器的相位变化,进而实现高精度轨迹重建。该方法依赖于角反射器在脉冲压缩域的高信杂比,以保证相位提取精度。而圆形轨迹使目标的距离徙动较之直线SAR更大,当角反射器RCS较弱时,在脉冲压缩域其信号容易淹没在周围杂波中。
针对这一问题,本文提出了一种基于图像域相位误差估计的圆迹SAR聚焦方法。该方法通过在场景中放置定标器,首先对场景进行粗成像,在图像域对散焦的定标器图像加窗,减小杂波的干扰,然后根据重建回波的方法估计中心波数相位误差和距离徙动误差,最后将残余运动误差引起的相位误差补偿至原始回波中,完成图像的聚焦。该方法不依赖于定标器回波有较高的信杂比,通过图像域加窗实现信号和杂波的分离,提高估计精度。 2 相位误差信号模型
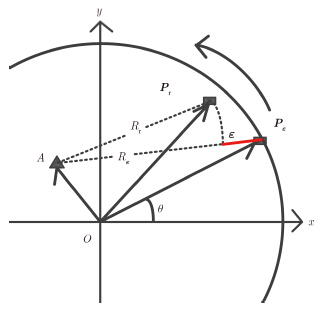
图 1为圆迹SAR运动模型(俯视图),平台围绕场景中心O做圆周运动,其位置向量与x轴的夹角为方位角$\theta $。
|
图 1 圆迹SAR运动模型 Fig.1 CSAR working mode |
根据导航系统得到的雷达测量坐标为${P}_\varepsilon(\theta)$,而其真实坐标为${{P}_{\rm{r}}}(\theta )$。若场景中有一点目标A,其坐标为PA,则残余运动误差使目标A的距离徙动产生误差:
| ${\varepsilon _A}(\theta ) = |{{P}_\varepsilon }(\theta ) - {{P}_A}| - |{{P}_{\rm{r}}}(\theta ) - {{P}_A}|$ | (1) |
| $\left. \begin{array}{l} {S_\varepsilon }(\theta ,K){\rm{ = }}{S_0}(\theta ,K){\rm{exp}}\{ {\rm{j}}{\phi _\varepsilon }(\theta ,K)\\ {\phi _\varepsilon }(\theta ,K) = 2K\varepsilon (\theta ) \end{array} \right\}$ | (2) |
| 表 1 仿真参数 Tab. 1 Simulation Parameters |
本文的目标是通过信号处理,估计相位误差${\phi _\varepsilon }(\theta ,K)$并补偿至原始回波${S_0}(\theta ,K)$中,再通过雷达测量坐标${{P}_\varepsilon }(\theta )$进行成像。首先从图像域的角度分析相位误差${\phi _\varepsilon }(\theta ,K)$与图像频谱的关系。
理想情况下,由理想回波${S_0}(\theta ,K)$成像所得的图像为g0(x,y),假设场景中仅存在单个点目标A,忽略发射信号和成像几何引起对点扩展函数的影响,g0(x,y)应为冲击函数:
| ${{g}_{\rm{0}}}(x,y) = {δ} (x - {x_A},y - {y_A})$ | (3) |
(xA,yA)为A的坐标,则理想图像g0(x,y)的2维波数域频谱仅包含关于(xA,yA)的线性相位,其中Kx,Ky为x,y方向的波数:
| $\begin{aligned} {S_A}({K_x},{K_y})& = \!\! \iint\limits_{xy} {{{g}_0}(x,y)\exp \{ - {\rm{j}}{K_x}x - {\rm{j}}{K_y}y\} {\rm{d}}x{\rm{d}}y} \\ & = \exp \{ - {\rm{j}}{K_x}{x_A} - {\rm{j}}{K_y}{y_A}\} \end{aligned}$ | (4) |
假设由误差回波${S_\varepsilon }(\theta ,K)$成像得到的误差图像为${g_\varepsilon }(x,y)$,则其2维频谱为:
| ${S_\varepsilon }({K_x},{K_y}) = \iint\limits_{xy} {{g_\varepsilon }(x,y)\exp \{ - {\rm{j}}{K_x}x - {\rm{j}}{K_y}y\} {\rm{d}}x{\rm{d}}y}$ | (5) |
由于${S_\varepsilon }(\theta ,K)$中包含的相位误差${\phi _\varepsilon }(\theta ,K)$随着成像过程引入误差图像${g_\varepsilon }(x,y)$中,其在图像域(x,y)的表现形式难以解析表达,但图像的2维波数域(Kx,Ky)和相位误差所在的角度-距离$(\theta ,K)$波数域可通过时频关系建立联系。
忽略发射信号频谱的包络和目标自身相位,则误差回波${S_\varepsilon }(\theta ,K)$为:
| ${S_\varepsilon }(\theta ,K){\rm{ = }}\exp \{ - {\rm{j}}2K{R_{A{\rm{e}}}}(\theta )\} $ | (6) |
| $\begin{aligned} {R_{A{\rm{e}}}}(\theta ) = & \left| {\mathop {{{P}_\varepsilon }}\limits (\theta ) - \mathop {{{P}_A}}\limits } \right|{\rm{ = }} \{ {{({x_{\rm{e}}}(\theta ) - {x_A})}^2} \\ & + {{({y_{\rm{e}}}(\theta ) - {y_A})}^2} + {{({z_{\rm{e}}}(\theta ) - {z_A})}^2} \} ^{\rm{1/2}} \end{aligned}$ |
| $\left. \begin{array}{l} {K_x} = \frac{{\partial \phi }}{{\partial {x_{\rm{e}}}}} = - 2K\frac{{{x_{\rm{e}}}(\theta ) - {x_A}}}{{{R_{A{\rm{e}}}}(\theta )}}\\ {K_y} = \frac{{\partial \phi }}{{\partial {y_{\rm{e}}}}} = - 2K\frac{{{y_{\rm{e}}}(\theta ) - {y_A}}}{{{R_{A{\rm{e}}}}(\theta )}} \end{array} \right\}$ | (7) |
由式(7)得,(Kx,Ky)不仅是相位误差${\phi _\varepsilon }(\theta ,K)$中$(\theta ,K)$的函数,也与目标位置(xA,yA)有关。因此相位误差${\phi _\varepsilon }(\theta ,K)$在波数域(Kx,Ky)的表现形式与${S_\varepsilon }({K_x},{K_y})$和SA(Kx,Ky)2维频谱的相位误差是等价的,即:
| $\begin{aligned} {\phi _\varepsilon }(\theta ,K) & = \arg \{ {S_\varepsilon }({K_x},{K_y})S_A^*({K_x},{K_y})\} \\ & = \arg \Bigg\{ \iint\limits_{xy} {{g_\varepsilon }(x,y)\exp [- {\rm{j}}{K_x}(x - {x_A})} \\ & \quad - {\rm{j}}{K_y}(y - {y_A})]{\rm{d}}x{\rm{d}}y \Bigg\} \end{aligned}$ | (8) |
| $\begin{aligned} {\phi _\varepsilon }(\theta ,K) & = \arg \Bigg\{ \iint\limits_{xy} {{g_\varepsilon }(x,y)\exp \! \bigg[\! - {\rm{j}}K} \\ & \! \cdot \frac{{({x_{\rm{e}}} - {x_A})(x - {x_A}) + ({y_{\rm{e}}} - {y_A})(y - {y_A})}}{{{R_{A{\rm{e}}}}(\theta )}} \! \bigg] \! {\rm{d}}x{\rm{d}}y \! \! \Bigg\} \end{aligned}$ | (9) |
式(9)中:
| $ \frac{{({x_{e}} - {x_A})(x - {x_A}) + ({y_{e}} - {y_A})(y - {y_A})}}{{{R_{A{\rm{e}}}} \ ({θ} )}}\\ \quad \ \ \approx \frac{{R_{A{\rm{e}}}^2({θ} ) - {R_{A{\rm{e}}}} \ ({θ} ){R_{xy}} \ ({θ} )}}{{{R_{A{\rm{e}}}} \ ({θ} )}}\\ \quad \ \ = {R_{A{\rm{e}}}} \ ({θ} ) - {R_{xy}}({θ} ) $ | (10) |
| ${\phi _\varepsilon }(\theta ,K) = \arg \{ \exp [{\rm{j}}2K{R_{A{\rm{e}}}}(\theta )] \cdot \mathop \int\!\!\!\int \limits_{xy} {g_\varepsilon }(x,y)\exp [ - {\rm{j}}2K{R_{xy}}(\theta )]{\rm{d}}x{\rm{d}}y\} $ | (11) |
因此,相位误差${\phi _\varepsilon }(\theta ,K)$ 和误差图像${g_\varepsilon }(x,y)$通过式(11)产生联系,由于式(6)可写为:
| $\begin{aligned}{S_\varepsilon }(\theta ,K) & {\rm{ = }} \exp \{ - {\rm{j}}2K{R_{A{\rm{e}}}}(\theta )\} \\ & {\rm{ = }}\iint\limits_{xy} {{g_0}(x,y)\exp [- {\rm{j}}2K{R_{xy}}(\theta )]{\rm{d}}x{\rm{d}}y} \end{aligned}$ | (12) |
则式(11)简化为:
| ${\phi _\varepsilon }(\theta ,K) = \arg \{ {S_{\rm{r}}}(\theta ,K)S_\varepsilon ^ * (\theta ,K)\} $ | (13) |
| ${S_{\rm{r}}}(\theta ,K) = \iint\limits_{xy} {{g_\varepsilon }(x,y)\exp [- {\rm{j}}2K{R_{xy}}(\theta )]{\rm{d}}x{\rm{d}}y}$ |
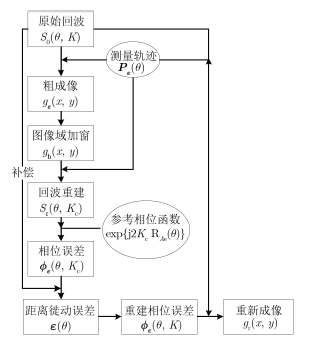
由式(11),相位误差${\phi _\varepsilon }(\theta ,K)$的估计需对误差图像${g_\varepsilon }(x,y)$进行2重积分,对于每个方位角${θ}$和距离向波数K,均需进行一次2重积分运算,因此估计参数为$({θ} ,K)$的${\phi _\varepsilon }(\theta ,K)$2维矩阵共需O(N4)乘法运算。由式(2)可知,${\phi _\varepsilon }(\theta ,K)$是关于K的线性相位函数,因此只需估计距离徙动误差${ε}({θ} )$即可对K降维,减少计算量至O(N3),而${ε} ({θ} )$可通过估计中心波数的相位误差${\phi _\varepsilon }(\theta ,{K_{\rm{c}}})$获得。因此${\phi _\varepsilon }(\theta ,K)$的估计可分为3步:(1)估计中心波数的相位误差${\phi _\varepsilon }(\theta ,{K_{\rm{c}}})$,(2)估计距离徙动误差${ε} ({θ} )$,(3)生成相位误差${\phi _\varepsilon }(\theta ,K)$。图 2为本文的算法流程图。通过以上步骤得到${\phi _\varepsilon }(\theta ,K)$的估计值并补偿至原始回波${S_0}({θ} ,K)$即可获得聚焦图像。
|
图 2 算法流程图 Fig.2 Algorithm flow chart |
将K=Kc代入式(11),得:
| ${\phi _\varepsilon }(\theta ,{K_c}) = \arg \{ \exp [{\rm{j}}2{K_0}{R_{A{\rm{e}}}}(\theta )] \cdot \mathop \int\!\!\!\int \limits_{xy} {g_\varepsilon }(x,y)\exp [ - {\rm{j}}2{K_0}{R_{xy}}(\theta )]{\rm{d}}x{\rm{d}}y\} $ | (14) |
中心波数相位误差${\phi _\varepsilon }(\theta ,{K_{\rm{c}}})$可通过在Kc处生成的单频回波${S_{\rm{r}}}(\theta ,{K_{\rm{c}}})$与图像峰值点处的参考相位函数${H_A}(\theta ,{K_{\rm{c}}})$共轭相乘得到:
| ${\phi _\varepsilon }(\theta ,{K_{\rm{c}}}){\rm{ = arg\{ }}{S_{\rm{r}}}(\theta ,{K_{\rm{c}}}) * H_A^*(\theta ,{K_{\rm{c}}}){\rm{\} }}$ | (15) |
| ${S_{\rm{r}}}(\theta ,{K_{\rm{c}}}) = \iint\limits_{xy} {{g_\varepsilon }(x,y)\exp [- {\rm{j}}2{K_{\rm{c}}}{R_{xy}}(\theta )]{\rm{d}}x{\rm{d}}y} $ | (16) |
${S_{\rm{r}}}(\theta ,{K_{\rm{c}}})$为以图像${g_\varepsilon }(x,y)$为目标的重建回波,在实际图像处理时,通常需要对图像${g_\varepsilon }(x,y)$进行加窗处理,以减少周围杂波的干扰,即令:
| ${g_{\rm{h}}}(x,y){\rm{ = }}{g_\varepsilon }(x,y){h_\varepsilon }(x - {x_A},y - {y_A})$ | (17) |
窗函数${h_\varepsilon }(x - {x_A},y - {y_A})$以点目标A位置(xA,yA)为中心。窗函数的宽度选择基于以下两个原则:(1)使窗内尽可能多的包含点目标A的信息,包括其散焦信息。(2)尽可能隔离窗外杂波对窗内目标的影响。
式(15)中:
| ${H_A}(\theta ,{K_{\rm{c}}}) = \exp \{ - {\rm{j}}2{K_{\rm{c}}}{R_{A{\rm{e}}}}(\theta )\} $ | (18) |
根据式(2),${\phi _\varepsilon }(\theta ,{K_c})$随$\varepsilon \left( \theta \right)$线性变化,可得:
| $\varepsilon \left( \theta \right) = \arg \{ {\phi _\varepsilon }(\theta ,{K_c})\} /2{K_{\rm{c}}} + 2N\pi , \\ \quad \quad \quad \quad N = 0, \pm 1, \pm 2, \cdots $ | (19) |
$\varepsilon \left( \theta \right)$ 以$2π$为周期进行卷绕,其主值难以确定。当方位向采样间隔满足Nyquist采样率时,相邻方位采样点的相位梯度不超过$2π$,即:
| $\arg \{ {\phi _\varepsilon }(q,{K_{\rm{c}}})*{\phi _\varepsilon }^*(\theta - \Delta \theta ,{K_{\rm{c}}})\} \in \left[ {0,2\pi } \right]$ | (20) |
| \[\tilde \varepsilon \left( \theta \right){\rm{ = }}\left\{ {\begin{array}{*{20}{l}} { - \frac{1}{{2{K_{\rm{c}}}}}\sum\limits_\theta {\arg \left\{ {{\phi _\varepsilon }\left( {\theta ,{K_{\rm{c}}}} \right)} \right.} }\\ {\quad \cdot \left. {\phi _\varepsilon ^*\left( {\theta - \Delta \theta ,{K_{\rm{c}}}} \right)} \right\},\quad \quad \theta \in \left( {0,2\pi } \right)}\\ {{\varepsilon _0},\quad \quad \theta = 0} \end{array}} \right.\] | (21) |
$\tilde \varepsilon \left( {\theta = 0} \right)$的初值${\varepsilon _0}$无法通过相位梯度法进行计算,其估计误差将引起型为$\exp \{ {\rm{j}}2K{\varepsilon _0}\} $的线性相位误差项,反映到脉冲压缩域,将使距离向包络产生常数${\varepsilon _0}$的偏移,虽不会影响以相干累积为原则的SAR图像的聚焦,但会使图像产生平移。
${\varepsilon _0}$的估计:由于计算中心波数相位误差${\phi _\varepsilon }(\theta ,{K_{\rm{c}}})$使$\varepsilon (\theta )$存在周期卷绕的问题,对于初值${\varepsilon _0}$我们则可以通过计算$\theta {\rm{ = }}0$时整个波数域带宽K内的相位误差${\phi _\varepsilon }(\theta = 0,K)$解决这一问题。根据式(11),有:
| $\begin{aligned} {\phi _\varepsilon }(\theta {\rm{ = }}0,K) = & \arg \Bigg\{ \exp [{\rm{j}}2K{R_{A{\rm{e}}}}(0)]\\ & \cdot \iint\limits_{xy} {{g_\varepsilon }(x,y)\exp [- {\rm{j}}2K{R_{xy}}(0)]{\rm{d}}x{\rm{d}}y \Bigg\} } \\ = & 2K{\varepsilon _0} \end{aligned}$ | (22) |
对${\phi _\varepsilon }(\theta = 0,K)$沿K方向进行逆傅里叶变换到脉冲压缩域得到点目标A的距离压缩曲线${l_A}(\theta = 0,r) = \mathop {{\rm{IFFT}}}\limits_K \{ {\phi _\varepsilon }(\theta = 0,K)\} $,提取其峰值位置即可得到初始距离徙动误差${\varepsilon _0} $:
| ${\varepsilon _0}{\rm{ = }}\arg \mathop {\max }\limits_r \{ \left| {{l_A}(\theta = 0,r)} \right|\} $ | (23) |
前两节通过估计重建回波的方法估计了中心波数相位误差${\phi _\varepsilon }(\theta ,{K_{\rm{c}}})$,并结合相位梯度法计算整个合成孔径内的距离徙动误差$\widetilde \varepsilon (\theta )$。根据式(2),由残余运动误差引起的整个波数域K内的相位误差为${\tilde \phi _\varepsilon }(\theta ,K){\rm{ = }}2K\tilde \varepsilon (\theta )$。
误差补偿即预先在原始回波${S_0}(\theta ,K)$的基础上与相位误差项$\exp \{ {\rm{j}}{\widetilde \phi _\varepsilon }(\theta ,K)\} $共轭相乘,作为后续成像处理的回波数据,以消除残余运动误差的影响。
| ${S_1}(\theta ,K) = {S_0}(\theta ,K)\exp \{ {\rm{j}}\widetilde \phi ^* \!\!\! _\varepsilon (\theta ,K)\} $ | (24) |
下面将给出本文提出的基于图像域相位误差估计的圆迹SAR聚焦算法的仿真实验结果,验证算法的有效性,并将算法应用于机载圆迹SAR实际数据的处理。仿真参数见表 1。
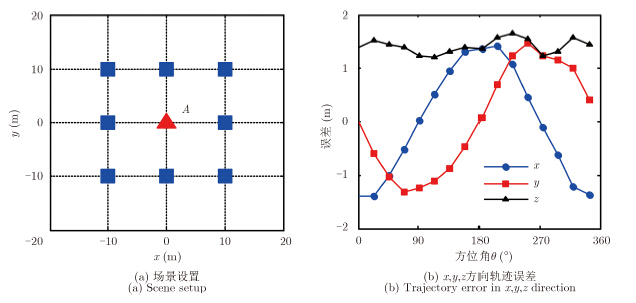
场景中设置9个点目标,其分布如图 3(a)所示,中心目标A位于(0,0)处,相邻目标x,y方向间隔为10 m。图 3(b)为雷达测量位置${{P}_\varepsilon }(\theta )$相对雷达真实位置${{P}_{\rm{r}}}(\theta )$在x,y,z 3个方向的运动误差。
|
图 3 仿真参数 Fig.3 Simulation parameters |
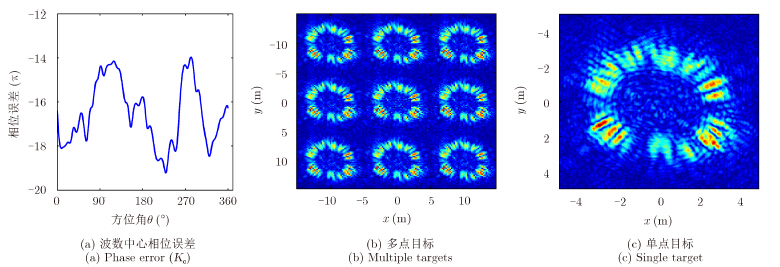
图 4(a)为残余运动误差相对点目标A引起的中心波束相位误差${\phi _\varepsilon }(\theta ,{K_{\rm{c}}})$,其均值和方差分别为16.5 π和2.02 π。图 4(b)为9个点目标的误差图像。可以看到,由于相位误差存在直流分量,使得图像呈现圆环状,且误差幅度远大于聚焦要求的λ/16,散焦情况严重。
|
图 4 相位误差及误差图像 Fig.4 Phase error and error images |
根据图 4(b)的误差图像,选取以点A目标中心,5 m×5 m大小的窗,进行截取后获得如图 4(c)的点目标A加窗误差图像gh(x,y)。通过gh(x,y)进行回波重建得到波束中心相位误差的估计值${\widetilde \phi _\varepsilon }(\theta ,{K_{\rm{c}}})$,其与真实值${\phi _\varepsilon }(\theta ,{K_{\rm{c}}})$之间的差如图 5(a)所示,其均值为0.06 π,方差2×104 π ,因此,基于图像域数据估计相位误差能够控制在较高的精度。图 5(b)为根据式(11)在 θ=0 时重建的点目标A脉冲压缩域回波,根据式(23),初始距离徙动误差${\varepsilon _0}$的估计值为1.98 m,而仿真真实值为1.9827 m。图 5(c)为进行相位补偿后的图像,可以看出点目标A及其周围目标都得到了良好的聚焦。
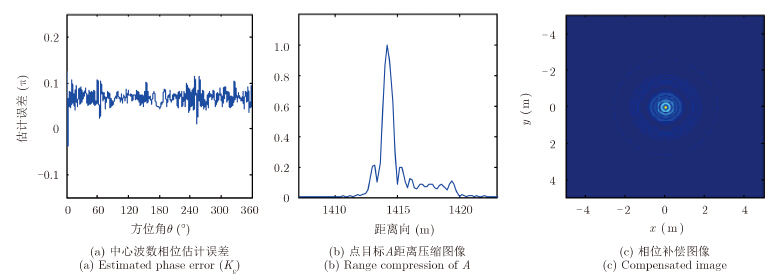
|
图 5 相位补偿后图像 Fig.5 Compensated image |
由于试验时场景中并无放置各项同性的角反射器,本文利用在机载圆迹SAR数据中人为加入理想点目标的回波来验证算法的有效性。图 6(a)为P波段机载圆迹SAR部分场景的全孔径成像结果,大小为800 m×800 m。图像中心的亮点为人为加入的理想点目标。图 6(b)为以点目标为中心,30 m×30 m的成像结果。以图 6(a)作为理想图像,其飞行轨迹作为真实轨迹,在此基础上,加入轨迹测量误差,得到如图 7(a)的成像结果。理想图像图 6(a)建筑物轮廓分明,而散焦图像图 7(a)模糊严重,目标难以识别。以点目标为中心对散焦图像进行加窗,如图 7(b),作为回波生成的误差图像。图 8(a)和图 8(b)分别为根据本文算法进行相位补偿的成像结果和相位误差的估计值。可以发现补偿图像中的点目标和整个场景均得到了良好的聚焦,而相位误差也得到了准确的估计。我们分别计算3幅图像的Reyni熵,作为图像聚焦效果的评价参数,其结果如表 2所示。熵值越高表示图像的散焦程度越高。经过相位补偿的图像熵值和原始图像较接近,但仍存在误差。

|
图 6 理想场景与点目标 Fig.6 Images without error |

|
图 7 散焦场景与点目标 Fig.7 Images defocused |
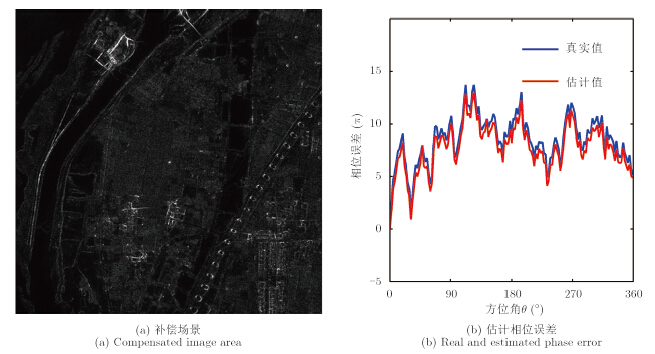
|
图 8 相位误差估计与补偿 Fig.8 Phase error estimation and compensation |
| 表 2 Reyni熵 Tab. 2Reyni Entropy |
由于现有导航系统精度有限,圆迹SAR的残余运动误差成为制约SAR图像聚焦的关键问题,通常基于回波数据提取特显点相位误差的方法对信噪比要求较高。针对这一问题,本文首先分析了残余运动误差引起的相位误差信号模型,引出了相位误差和误差图像频谱的关系。然后通过对误差图像选取特显点,利用特显点图像加窗并重建回波,估计中心波数相位误差以及距离徙动误差,最后将相位误差补偿至回波中,实现跨距离分辨单元的残余运动误差补偿,完成场景的聚焦。该方法的有效性通过本文的仿真和实际机载数据得到了验证。
| [1] | Soumekh M. Synthetic Aperture Radar Signal Processing[M]. New York: John Wiley & Sons, 1999: 486-539.( 1) 1) |
| [2] | Chan T K, Kuga Y, and Ishimaru A. Experimental studies on circular SAR imaging in clutter using angular correlation function technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2192-2197.( 1) 1) |
| [3] | Axelsson S R J. Beam characteristics of three-dimensional SAR in curved or random paths[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10): 2324-2334.( 1) 1) |
| [4] | Pinheiro M, Prats P, Scheiber R, et al.. Tomographic 3D reconstruction from airborne circular SAR[C]. IEEE International Geoscience and Remote Sensing Symposium, 2009, 3: III-21-III-24.( 1) 1) |
| [5] | Ferrara M, Jackson J A, and Austin C. Enhancement of multi-pass 3D circular SAR images using sparse reconstruction techniques[C]. Proceedings SPIE Algorithms for Synthetic Aperture Radar Imagery, 2009, DOI: 10.1117/12.820256.( 1) 1) |
| [6] | 洪文. 圆迹 SAR 成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135. Hong Wen. Progress in circular SAR imaging technique[J]. Journal of Radars, 2012, 1(2): 124-135.(  1) 1) |
| [7] | Frolind P, Gustavsson A, Lundberg M, et al.. Circular-aperture VHF-band synthetic aperture radar for detection of vehicles in forest concealment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(4): 1329-1339.( 1) 1) |
| [8] | Frolind P, Ulander L M H, Gustavsson A, et al.. VHF/UHF-band SAR imaging using circular tracks[C]. IEEE International Geoscience and Remote Sensing Symposium, 2012: 7409-7411.( 1) 1) |
| [9] | Casteel Jr C H, Gorham L R A, Minardi M J, et al.. A challenge problem for 2D/3D imaging of targets from a volumetric data set in an urban environment[C]. Proceedings SPIE Algorithms for Synthetic Aperture Radar Imagery, 2007, DOI: 10.1117/12.731457.( 1) 1) |
| [10] | Ertin E, Austin C D, Sharma S, et al.. GOTCHA experience report: Three-dimensional SAR imaging with complete circular apertures[C]. Proceedings SPIE Algorithms for Synthetic Aperture Radar Imagery, 2007, DOI: 10.1117/12.723245.( 1) 1) |
| [11] | Ponce O, Prats-Iraola P, Pinheiro M, et al.. Fully polarimetric high-resolution 3-D imaging with circular SAR at L-ban[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3074-3090.( 1) 1) |
| [12] | Lin Y, Hong W, Tan W, et al.. Airborne circular SAR imaging: results at P-band[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium, 2012: 5594-5597.( 1) 1) |
| [13] | 林赟, 谭维贤, 洪文, 等. 圆迹SAR极坐标格式算法研究[J]. 电子与信息学报, 2010, 32(12): 2802-2807. Lin Yun, Tan Wei-xian, Hong Wen, et al.. Polar format algorithm for circular synthetic aperture radar[J]. Journal of Electronics & Information Technology, 2010, 32(12): 2802-2807.(  1) 1) |
| [14] | Demirci S, Yigit E, and Ozdemir C. Wide-field circular SAR imaging: 2D imaging results for simulation data[C]. IEEE 2013 6th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, 2013: 421-424.( 1) 1) |
| [15] | Poisson J B, Oriot H, and Tupin F. Performances analysis of moving target tracking in circular SAR[C]. 2013 14th International IEEE Radar Symposium (IRS), Dresden, 2013: 531-536.( 1) 1) |
| [16] | Cantalloube H and Koeniguer E C. Assessment of physical limitations of high resolution on targets at X-band from circular SAR experiments[C]. 7th European Conference on Synthetic Aperture Radar (EUSAR 2008), Friedrichshafen, 2008: 1-4.( 1) 1) |
 2015, Vol. 4
2015, Vol. 4
