②(中国科学院大学 北京 100049)
③(中国科学院上海高等研究院 上海 201203)
②(University of Chinese Academy of Sciences, Beijing 100049, China)
③(Shanghai Advanced Researched Institute, University of Chinese Academy of Sciences, Shanghai 201203, China)
实时成像系统分辨率要求不断提高,而雷达回波数据中的高次相位误差导致图像散焦、对比度降低和几何失真等问题,因此要获得高分辨图像,须对高次相位误差进行补偿[1, 2, 3, 4]。
自聚焦算法中,相位梯度自聚焦算法(Phase Gradient Autofocus,PGA)可有效补偿高次相位误差,但一般需要迭代多次,运算耗时,且在不同场景的应用中算法的聚焦性能不够稳定。
文献[5]提出一种组合实时PGA算法,先利用SACGS和SAC对二次相位误差进行精确补偿,以使后续PGA算法避免迭代。本文直接针对PGA多次迭代的因素进行改进。
PGA算法的聚焦性能及收敛速度由相位误差的估计精度决定,而算法中选点的孤立性及窗函数的宽度对相位误差的估计精度有很大影响。因此,选点及窗宽估计是影响PGA性能的关键因素。
传统的选点方法在每个距离单元选一个最大值点,然而能量大的点可能不是孤立点。文献[6]在频域定义对比度准则进行选点,该方法运用较广泛,但运用该准则前需先将图像域的信号变换到距离压缩相位历史域,其中涉及大量FFT和IFFT操作,运算耗时,实时成像要求尽量避免这些操作。文献[7]在图像域利用滑窗结构选点,该方法在进行点目标质量评估时需截取散焦点的数据,其中数据截取的宽度固定取1-2个分辨单元,由此当处理散焦程度不同的图像时,固定宽度可能截取不到完整的数据,从而导致选点方法性能下降或失效。文献[8]改进选点方式,但在选点过程中亦使用了固定窗宽。本文提出一种基于数据均值的选点方法,在图像域选点,流程简单且省时。该方法对点目标进行评估时也需要截取散焦点数据,但点散焦的宽度根据均值估计而来,可根据数据的变化自适应调整,因此即使处理不同散焦程度的图像,该方法均能有效选出孤立性强的点,提高相位误差估计的精度,从而使算法获得稳定的聚焦性能,并有效减少迭代次数。
传统的加窗方法一是设定一个较大的初始窗宽,每次迭代时按一定比例递减,然而初始窗宽一般设置得过于粗放,算法收敛速度慢。第2种方法通过累加各个距离行上的能量得到1维函数,然后将函数峰值下降到10 dB处的宽度再展宽50%作为窗宽[9]。然而10 dB宽度并不适用于各种散焦程度的图像。文献[10]提出利用1维函数均值与函数远端均值估计窗宽。 其他一些加窗方法[11, 12]亦多基于1维能量函数进行改进。能量函数是大量距离单元累加的平均结果,当场景中个体差异较大时,较难从中确定出一个合适的宽度用于对所有点进行统一加窗。本文提出基于脉冲包络的窗宽估计方法,该方法可自适应地获取对每个散射点加窗的合适宽度,有效提高相位误差估计的精度,从而使算法获得稳定的聚焦性能,并有效减少迭代次数。
本文对选点和窗宽估计方法的自适应性能进行了加强,使PGA算法在不同场景的应用中均能较准确地估计相位误差,克服了PGA聚焦性能不稳定、多次迭代的难点。在运算时间方面,传统的基于对比度准则选点及基于能量函数10 dB宽度的PGA算法中,选点及窗宽估计的运算时间在PGA算法总运算时间中占据很大一部分比例,本文提出的选点和窗宽估计方法有效降低了这两部分的运算处理时间,使PGA算法的整体运算效率得到显著提升,使其更适合于实时处理。
2 条带SAR的PGA算法原理
PGA最初针对聚束SAR提出[9]。在聚束SAR中,复图像数据和相位历程是傅里叶变换对的关系,任何点的相位历程均包含了整个方位向相位误差。条带SAR中,点目标的相位历程经过方位维成像的逆过程获取,其中只包含相位误差的一段,且相位误差存在2维空变性。将PGA运用于条带SAR一般有2种方法[13]:一是变换条带SAR数据[14, 15, 16],使其具有与聚束SAR相似的特性后再运用标准PGA算法;二是改变PGA算法[17, 18],使之适用于条带SAR数据。本文采用第2种方法,先在条带SAR图像中选取强散射点,接着直接以各点为中心,加窗后与参考线性调频信号进行卷积,恢复其方位压缩前的数据[18],然后以点目标原位置为中心对数据截取一个合成孔径长度进行解线频调脉压,之后再根据标准PGA算法流程估计相位误差的梯度,最后通过拼接各点的相位误差的梯度得到整幅图像的相位误差。 该方法的具体流程如下:
第1步 分块 将图像数据沿距离向分块,满足每块内相位误差的距离向空变性可忽略。再对每个距离块沿方位向进行分块,满足每块内相位误差的方位向空变性可忽略。
第2步 选点 在每个子块内选取孤立强点,因为孤立强点具有较高的信噪比和信杂比,有利于准确地估计相位误差。
以选取的点为中心加窗后与参考线性调频信号进行卷积,经过成像的逆过程恢复其方位压缩前的数据,此时存在相位误差的点目标信号模型表示为:
| $g(u) = \left| {g(u)} \right| \cdot \exp \left( {{\rm{j}}\left[{\theta (u) + {\phi _{\text{e}}}(u)} \right]} \right)$ | (1) |
以点目标原位置为中心对方位压缩前的数据截取一个合成孔径长度,然后用解线频调进行脉冲压缩,压缩后在频域得到一个散焦的脉冲。
第3步 圆移 将频域点脉冲圆移至零频,以此去除相位中的线性项。
第4步 加窗 对圆移后的点脉冲进行加窗,以消除高频噪声和邻近杂波的干扰。如果窗宽太大,会引入过多的噪声,信杂比低,影响估计的准确性,迭代次数增加;如果窗过小,则截取不到完整的散焦信息,导致所估计的相位误差失真,甚至造成估计发散。
第5步 相位误差估计 对加窗后的点脉冲信号做IFFT后q(u)中只剩下一个固定相位项,设此时的信号为g1(u),通过求g1(u)序列的相关序列rn(u)即可获得相位误差的梯度[19]:
| ${r_n}(u) = {g_1}(u) \cdot g_1^*(u - 1) = \left| {{r_n}(u)} \right| \cdot \exp [{Δ} {\phi _{\rm{e}}}(u)]$ | (2) |
将所有点目标的相关序列rn(u)按其所在位置求平均[20],得到整个方位向相位误差的梯度${Δ} {\varphi _{\text{e}}}(u)$,将该梯度中的固定项去掉后再求和,得相位误差:
| ${\hat \varphi _{\rm{e}}}(u) = \sum\limits_{m = 1}^u {{Δ} {\varphi _{\rm{e}}}(m)} $ | (3) |
对以上5步进行迭代,直到估计出的相位误差其影响可忽略不计为止。
3 自适应的选点及窗宽估计方法选点和加窗操作是PGA算法中的关键步骤,当操作中使用的参数与待处理数据失配时,相位误差估计的准确度将下降,由此导致算法的迭代次数增加。失配严重时可能产生额外的相位误差,导致算法的聚焦性能不稳定。因此要提高算法的自适应性能,则选点及加窗操作中使用的各参数值应从数据中获取,使其可跟随数据自适应调整,从而使算法在处理不同数据时均能准确地估计出相位误差,以此获得稳定的聚焦性能并有效减少迭代次数。即使某些参数需要使用经验值,这些经验值也应具有普适性。并且,在个体目标差异较大的复杂的大场景中,各参数值还需因点而异,与各点相匹配。基于以上分析,本文提出了基于数据均值的自适应选点方法和基于脉冲包络的自适应窗宽估计方法。
3.1 基于数据均值的自适应选点方法相位误差使点散布函数的主瓣朝展宽的方向发展,旁瓣升高,严重时旁瓣可能被吸纳进主瓣,因此,受相位误差影响的点散布函数,其波形将呈现内底部空洞的钟型形态,如图 1(a)所示。因此,若将距离单元内数据幅度的均值作基线,则其与点散布函数底部边缘相交时所确定的宽度可反映点散布函数的展宽宽度。对于孤立散射点,此宽度即为点散布函数的展宽宽度,此宽度外主要分布着幅度相对较低的杂波。对于非孤立散射点,多点目标的主旁瓣相互叠加,波形被分割成许多窄波,如图 1(b)所示。此时,幅度最大的像素点所在的窄波与均值线相交所确定的宽度内仅包含散射点部分能量,该宽度周围仍有大量强信号。
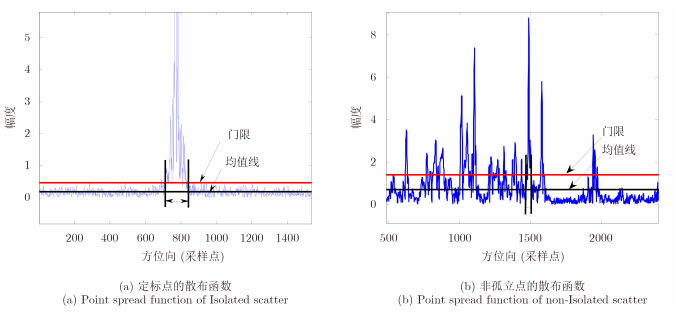
|
图 1 点散布函数 Fig.1 Point spread function in azimuth |
用瑞利分布对杂波进行建模,杂波幅度的概率密度函数为:
| $f(x;\sigma ) = \frac{x}{{{\sigma ^2}}}{{\rm{e}}^{ - {x^2}/2{\sigma ^2}}},\quad x ≥ 0$ | (4) |
| $\mu = \sigma \sqrt {{{π} \mathord{\left/ {\vphantom {{π} 2}} \right.} 2}} $ | (5) |
设杂波幅度超过门限Ar的概率不大于P :
| $\;1 - \int\nolimits_0^{{A_{\text{r}}}} {f\left( {x;\sigma } \right)} {\rm{d}}x ≤ P\;$ | (6) |
若散射点为孤立散射点,因其周围为杂波,则根据杂波模型,其散布函数展宽宽度外幅度超过门限Ar的点的比例将小于P,如图 2中阴影部分所示。否则说明该散射点为非孤立点,因其周围除了杂波,还存在大量强信号,由此使得散布函数展宽宽度外幅度超过门限Ar的点的比例超过P。
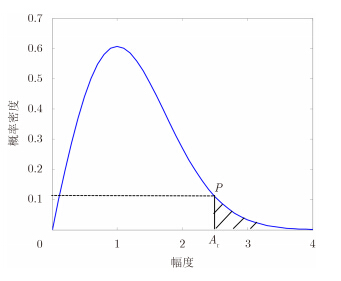
|
图 2 杂波幅度的瑞利分布模型 Fig.2 Probability density function of clutter |
选点的流程为:
第1步 估计散布函数展宽宽度 计算距离单元内所有数据幅度的均值,记录距离单元内最大值点的方位位置,然后从最大值位置开始向两边搜索,找到第1个幅度小于均值的像素点,则最大值点两边满足该条件的两个像素点p1和pr间的距离即为散布函数的展宽宽度。
第2步 确定门限 根据距离单元内数据幅度的均值计算s,设杂波幅度超过门限的概率为P(该值可根据实际情况设定,本文取30%),则由式(6)确定门限值Ar。
第3步 评判散射点孤立性统计 p1和pr两点外幅度值超过门限的像素点数,若该数目占统计样本总点数的比例小于P,则该强点为孤立散射点。若该数目占统计样本总点数的比例大于P,则为非孤立散射点,将其排除。
3.2 基于脉冲包络的自适应窗宽估计方法经解线频调压缩后的窄脉冲受高阶相位误差的影响,多个旁瓣升高,波形畸变失去对称性,如图 3中蓝线所示。此时,利用门限或1维能量函数等常规方法较难确定一个合适的加窗宽度。本文考虑到脉冲包络的宽度易于估计,且能较准确地反映脉冲的散焦宽度。因此若以包络的宽度作为加窗的宽度,则可有效截取到完整的点目标信号,并消除附近杂波及高频噪声的干扰。
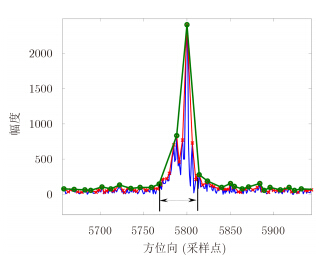
|
图 3 频域定标点的脉冲波形 Fig.3 Point spread function in frequency domain |
根据以上分析,估计窗宽的操作步骤为:
第1步 提取脉冲包络 波形中的极大值点可体现脉冲的包络,因此先求脉冲信号的1阶前向差分,得到的差分序列中符号由正变到负的点即为极大值点,如图 3中红色加号所示。极大值点在波形的最上端,因此极大值点的连线可体现脉冲的包络。考虑到散焦严重的情况下,波形存在较大的起伏,此时的包络将不够平滑,其宽度仍较难估计,由此,再对包络进行前向差分,得到包络的极大值点,如图 3中绿色星号所示,此时的包络已相对较平滑。
第2步 估计窗宽 通过检测包络极大值点中第1个变化平缓的点即可求得包络的宽度,然后将此宽度作为对脉冲加窗的宽度。
3.3 基于自适应选点及窗宽估计的改进PGA算法基于自适应选点及窗宽估计的改进PGA算法流程如图 4(a)所示,传统PGA算法的流程如图 4(b)所示。其中传统PGA算法采用基于对比度准则的选点方法,并通过累加各个距离行上的能量得到1维函数,将函数峰值下降到10 dB处的宽度再展宽50%作为窗宽。
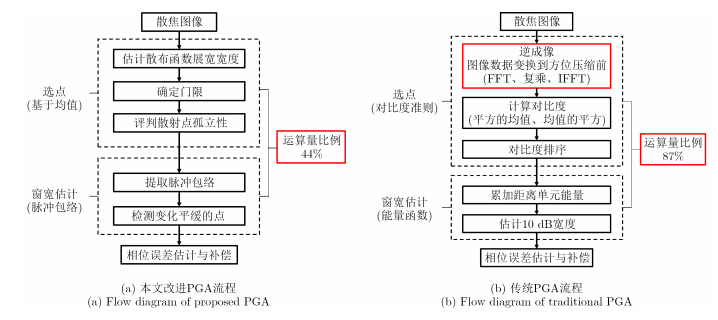
|
图 4 传统PGA与本文改进PGA算法流程 Fig.4 Flow diagram of traditional PGA and proposed PGA |
基于自适应选点及窗宽估计的改进PGA算法可获得较稳定的聚焦性能。由于选点方法中点散布函数的扩展宽度由数据均值估计得出,保证了选点方法在不同散焦程度图像应用中的有效性,由此算法的稳定性得到了提高。由于对脉冲加窗的宽度即为估计的脉冲包络宽度,避免了当处理散焦程度不同的图像时固定窗宽与待处理数据失配的问题,由此算法的稳定性得到了提高。选点及窗宽估计方法自适应性能的加强,使PGA算法在不同场景的应用中均能较准确地估计相位误差,从而获得稳定的聚焦性能。
4.2 算法的复杂度分析(1) 改进的PGA算法运算量显著减少。
设图像方位向点数为M,距离向点数为N,合成孔径长度为Ls,点散布函数的扩展宽度为L,选取的点数为n,脉冲的极大值点数为l。本文改进的PGA算法的运算量与传统PGA算法的运算次数如表 1所示。本文提出的选点方法直接在图像域选点,而传统的基于对比度准则的选点方法需先将图像域的信号变换到距离压缩相位历史域,涉及额外的FFT、复乘和IFFT操作,因此在选点方面本文方法的运算量远小于传统方法的运算量。传统的窗宽估计方法需要累加各个距离行上的能量,本文提出的窗宽估计方法针对选取的散射点,即只对部分距离单元的数据进行估计,降低了运算量。
| 表 1 本文选点方法与对比度准则选点方法的运算次数 Tab.1 Operational volume of proposed method and the contrast criteria |
用本文改进PGA算法与传统PGA算法处理一幅16384×2048图像,在相同运算资源的条件下,传统PGA算法中选点及窗宽估计的运算时间在PGA算法总运算时间中所占的比例高达87%,本文提出的选点和窗宽估计方法占PGA总时间的44%,有效降低了这两部分的运算处理时间,使PGA算法的整体运算效率得到显著提升,使其更适合于实时处理。
(2) 改进的PGA算法操作流程简单,适合实时成像。
传统PGA算法处理流程与本文改进的PGA算法处理流程如图 4所示。传统选点方法需要先将信号从图像域变换到方位压缩前,选点过程中涉及FFT、排序等运算,操作复杂。本文提出的选点方法直接在图像域操作,涉及比较运算与统计运算,操作相对简单。传统的窗宽估计方法需累加各个距离行上的能量后再进行窗宽估计,本文提出的窗宽估计方法在每个点加窗前进行,即窗宽的估计可嵌入到相位误差的估计中,这样更有利于并行计算的实施。
5 实测数据结果用平稳性不同的SAR平台获取的不同场景的图像数据测试本文提出方法的自适应性能,并与传统PGA算法处理结果进行了对比。其中传统PGA算法使用对比度准则进行选点,并通过累加各个距离行上的能量得到1维函数,将函数峰值下降到10 dB处的宽度再展宽50%作为窗宽。
图 5为Ku波段车载SAR系统获取的图像数据,图像方位向点数16384,距离向点数2048,成像理论分辨率0.3 m×0.3 m。载车速度约9 m/s,采用的惯性测量单元(Inertial Measurement Unit,IMU)和全球定位系统(Global Position System,GPS)的组合导航系统的定位误差精度约为5 cm。图 5(a)为利用导航数据运动补偿后的RDA成像结果,图像散焦较严重,主瓣展宽,旁瓣升高。图 5(b)为传统PGA迭代4次后的处理结果,图 5(c)为利用本文方法迭代2次后的聚焦图像,图 5(d)为图像上矩形框所示定标点在3种情况下的冲激响应的方位向幅度剖面。对比图可见,传统PGA算法聚焦效果较明显,点目标方位向冲激响应主瓣变窄,旁瓣降低,但本文方法的聚焦效果更显著,旁瓣被有效压低,主瓣更窄,分辨率可达到理论值。经分析,对于该幅图像,本文方法比传统PGA聚焦效果更好的原因主要是本文方法对窗宽的估计更准确,传统方法估计的窗宽为42个采样点。本文通过估计8个特显点脉冲的包络宽度,并将包络宽度的平均值作为加窗宽度,均值为60个采样点。两个窗宽值稍有差别,而聚焦效果差别较大,且当用本文估计的窗宽值赋给传统PGA算法进行处理时,其处理结果可以接近本文方法处理的效果。由此可见改进的PGA算法可更准确地估计窗宽,获得比传统PGA算法更优的聚焦性能。
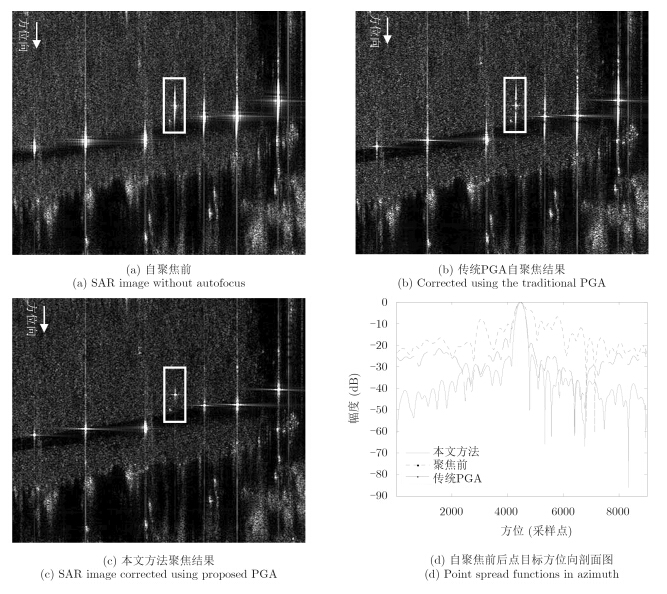
|
图 5 车载SAR图像聚焦结果 Fig.5 Focus performance |
图 6为无人机载SAR系统获取的图像数据,载机的速度约为31 m/s,飞行高度分别为1000 m和500 m,惯导定位精度约为1 cm。图 6(a)为利用运动传感器数据进行运动补偿后的图像,图像大小16384×2048。图 6(b)为传统PGA迭代4次聚焦结果,成像质量有一定改善。图 6(c)为本文方法迭代2次聚焦结果,成像质量明显改善。可见,改进PGA方法比传统PGA方法具有更强的自适应性,聚焦性能更稳定,由此可用于实时成像。

|
图 6 无人机载SAR图像聚焦结果 Fig.6 Focus performance |
针对现有PGA算法对图像场景或散焦程度自适应差的问题,本文对算法中关键的选点及加窗步骤进行了改进,提出了基于数据均值的选点方法及基于脉冲包络的窗宽估计方法,方法中使用的参数均可随数据的变换自适应调整。对此当图像数据变换时,算法均可准确地估计相位误差,实现快速收敛。对不同场景及散焦程度各异的实测SAR数据的处理结果证实了该算法具有较强的自适应性,可避免了人员参与手动调整,因此该方法可用于实时成像。
| [1] | 田雪, 梁兴东, 李焱磊, 等. 基于子孔径包络误差校正的SAR高精度运动补偿方法[J]. 雷达学报, 2014, 3(5): 583-590. Tian Xue, Liang Xing-dong, Li Yan-lei, et al.. High-precision motion compensation method based on the subaperture envelope error correction for SAR[J]. Journal of Radars, 2014, 3(5): 583-590.(  1) 1) |
| [2] | 张磊, 邓云凯, 王宇, 等. 基于代价函数的通道误差校正方法[J]. 雷达学报, 2014, 3(5): 556-564. Zhang Lei, Deng Yun-kai, Wang Yu, et al.. Channel error compensation for multi-channel sar based on cost function[J]. Journal of Radars, 2014, 3(5): 556-564.(  1) 1) |
| [3] | 高阳, 禹卫东, 冯锦, 等. 一种基于勒让德拟合的SAR后向投影自聚焦算法[J]. 雷达学报, 2014, 3(2): 176-182. Gao Yang, Yu Wei-dong, Feng Jin, et al.. A SAR back projection autofocusing algorithm based on legendre approximation[J].Journal of Radars, 2014, 3(2): 176-182.(  1) 1) |
| [4] | 折小强, 仇晓兰, 韩冰, 等. 一种基于变换域的滑动聚束SAR调频率估计方法[J]. 雷达学报, 2014, 3(4): 419-427. She Xiao-qiang, Qiu Xiao-lan, Han Bing, et al.. An improved doppler rate estimation approach for sliding spotlight sar data based on the transposition domain[J]. Journal of Radars, 2014, 3(4): 419-427.(  1) 1) |
| [5] | 张新, 丁赤飚, 吴一戎, 等. 一种用于条带式RD算法的组合实时PGA方法[J]. 电子与信息学报, 2007, 29(5): 1065-1068. Zhang Xin, Ding Chi-biao, Wu Yi-rong, et al.. A combined real time PGA method for strip map airborne SAR with RD algorithm[J].Journal of Electronics & Information Technology, 2007, 29(5): 1065-1068.(  1) 1) |
| [6] | Yadin E. SAR autofocusing viewed as adaptive beamforming on prominent scatters[C]. Record of 1994 IEEE National Radar Conference, Atlanta GA, 1994: 138-143.( 1) 1) |
| [7] | 李燕平, 邢孟道, 保铮. 一种改进的相位梯度自聚焦方法[J]. 西安电子科技大学学报(自然科学版), 2007, 34(3): 386-391. Li Yan-ping, Xing Meng-dao, and Bao Zheng. Improved phase gradient autofocus algorithm based on adaptive isolated scatter selection[J]. Journal of Xidian University, 2007, 34(3): 386-391.(  1) 1) |
| [8] | Fu Tuo, Gao Mei-guo, and He Yuan. An improved scatter selection method for phase gradient autofocus algorithm in SAR/ISAR autofocus[C]. Proceedings of the 2003 International Conference on Neural Networks and Signal Processing, Nanjing, China, 2003: 1054-1057.( 1) 1) |
| [9] | Wahl D E, Eichel P H, and Ghiglia D C. Phase gradient autofocus – a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electionic Systems, 1994, 30(3): 827-835.( 2) 2) |
| [10] | 倪崇, 王岩飞, 徐向辉, 等. 一种改进的SAR图像聚焦方法[J]. 测绘学报, 2012, 41(3): 449-453. Ni Chong, Wang Yan-fei, Xu Xiang-hui, et al.. An improved autofocus algorithm for SAR images[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 449-453.(  1) 1) |
| [11] | 林格, 刘明敬, 郝明. 改进的相位梯度自聚焦加窗方法[J]. 信息化研究, 2010, 36(7): 25-28. Lin Ge, Liu Ming-jing, and Hao Ming. Improved windowing method for phase gradient autofocus algorithm[J].Informatization Research, 2010, 36(7): 25-28.(  1) 1) |
| [12] | 闫龙, 郑妍, 李颜超. 改进的机载SAR相位梯度自聚焦算法[J]. 应用科技, 2012, 39(1): 39-43. Yan Long, Zheng Yan, and Li Yan-chao. Improved algorithm of phase gradient autofocus for air-borne synthetic aperture radar[J]. Applied Science and Technology, 2012, 39(1): 39-43.(  1) 1) |
| [13] | 李建阳, 常文革, 王亮. 一种应用于条带SAR的改进PGA算法[J]. 现代雷达, 2007, 29(8): 52-55. Li Jian-yang, Chang Wen-ge, and Wang Liang. A modified PGA algorithm used in stripmap SAR[J]. Modern Radar, 2007, 29(8): 52-55.(  1) 1) |
| [14] | Zhu Dai-yin, Jiang Rui, and Mao Xin-hua. Multi-Subaperture PGA for SAR autofocusing[J]. IEEE Transactions on Aerospace and Electionic Systems , 2013, 49(1): 468-488.( 1) 1) |
| [15] | Thompson D G, Bates J S, and Arnold D V. Extending the phase gradient autofocus algorithm for low-altitude Stripmap mode SAR[C]. Proceedings of the 1999 IEEE Radar Conference, Waltham, MA, 1999: 36-40.( 1) 1) |
| [16] | 蒋锐, 朱岱寅, 朱兆达. 一种用于条带模式SAR成像的自聚焦算法[J]. 航空学报, 2010, 31(12): 2385-2392. Jiang Rui, Zhu Dai-yin, and Zhu Zhao-da. A novel approach to strip-map SAR autofocus[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(12): 2385-2392.(  1) 1) |
| [17] | 孟大地, 丁赤飚. 一种用于条带式SAR的自聚焦算法[J]. 电子与信息学报, 2005, 27(9): 1349-1352. Meng Da-di and Ding Chi-biao. A new approach to autofocus considering strip map SAR[J]. Journal of Electronics & Information Technology, 2005, 27(9): 1349-1352.(  1) 1) |
| [18] | Wahl D E, Jakowatz Jr, C V, and Thompson P A. New approach to Strip-Map SAR autofocus[C]. 1994 Sixth IEEE Digital Signal Processing Workshop, Yosemite National Park, 1994: 53-56.( 2) 2) |
| [19] | Eichel P H, Ghiglia D C, and Jakowatz C V. Speckle processing method for synthetic-aperture- radar phase correction[J]. Optics Letters, 1989, 14(1): 1-3.( 1) 1) |
| [20] | Fienup J R. Phase error correction by shear averaging[C]. Signal Recovery and Synthesis II, Optical Society of America, 1989: 134-137.( 1) 1) |


