1 引言

合成孔径雷达( Synthetic Aperture Radar,SAR)采用脉冲压缩技术和合成孔径原理可实现对地面场景的成像，该成像具有全天候、全天时、远距离和宽测绘带的特点，因此在环境监测、资源勘查、测绘以及战场侦查等领域都发挥着重要作用^[1]。与正侧视SAR成像相比，斜视SAR成像在实用中具有更好的机动性。它通过改变天线波束的指向，可以对前方目标预先成像，对后方目标再次成像，从而便于在军事上实现实时侦察与打击、重访热点地区^{[2, 3, 4, 5]}。因此斜视SAR具有很高的军事价值，已经成为SAR成像技术的研究热点。

然而随着成像精度的不断提高，使得斜视SAR成像的原始回波数据量急剧增加。由于能源和重量的限制通常载机雷达不具有较强的A/D采样和数据处理能力，只能对回波数据进行一些简单的预处理，更为复杂的运算需要将回波数据信息传输给地面接收站进行整理和进一步的处理。庞大的数据量对SAR系统的存储和数据信道的传输能力提出了较高的要求。在保证高质量的斜视SAR成像的同时，如何降低A/D采样速率、减少原始数据量对于斜视SAR成像技术的进一步发展与应用具有重要意义。

压缩感知理论是由D. Donoho,E. Candes及华裔科学家T. Tao等人于2006年提出的，该理论表明，可以从严重降采样的数据中实现稀疏信号与数据以高概率的完美重构^{[6, 7]}。研究人员基于该特性将压缩感知理论应用于SAR成像中，进行SAR回波数据的压缩与成像处理，并取得了一定的成果^{[8, 9, 10, 11, 12, 13, 14]}。美国的Patel提出了一种基于压缩感知的SAR成像技术，利用少量的方位采样数据重建场景图像^[8]。西班牙的Alonso利用压缩感知处理取代传统的匹配滤波处理，在大幅减少SAR脉冲数的基础上实现了准确成像^[9]。土耳其的Cetin提出了一种场景幅度稀疏信息的SAR重建方法，通过联合优化问题求解重建场景幅度并估计场景相位^[10]。中科院电子所吴一戎院士团队研究了稀疏微波成像技术的理论体系，并论述了稀疏微波成像典型应用的研究进展^{[11, 12]}。国防科学技术大学的杨俊刚博士研究了随机频率信号的SAR成像，通过两维随机采样大幅减少了SAR成像的回波数据和频率资源^[13]。西安交通大学的方健博士基于距离多普勒成像算法提出了一种快速压缩感知SAR成像方法，能够在大幅减少回波采样数情况下实现高质量成像^[14]。北京航空航天大学的孙进平研究员提出了基于Poisson disk的非均匀采样的SAR成像方法^[15]，有效减少了脉冲重复频率实现了宽幅高分辨成像。

综上所述，虽然已有较多文献研究基于压缩感知SAR成像技术，但是这些工作主要是针对常规的SAR成像模式而言。还未有将压缩感知理论应用于大斜视SAR成像中的报道。在大斜视SAR成像中，由于回波信号存在大距离徙动以及距离向和方位向严重耦合的特点，使得现有应用于正侧视SAR成像的压缩感知处理方法无法有效适用。本文首先基于全采样回波数据给出一种大斜视SAR成像算法，通过走动补偿函数的构建和NCS补偿算法的应用有效解决了大斜视SAR数据中存在的大距离徙动和两维耦合问题，实现了准确成像。在此基础上进一步研究基于降采样数据的大斜视SAR成像问题，将提出的全采样成像算法构造成(Non-linear Chirp Scaling,NCS)算子，并基于该算子建立压缩感知成像模型，利用改进的迭代阈值算法(Iterative Thresholding Algorithm,ITA)实现了对成像模型的优化求解，进而获得了最终的成像结果。

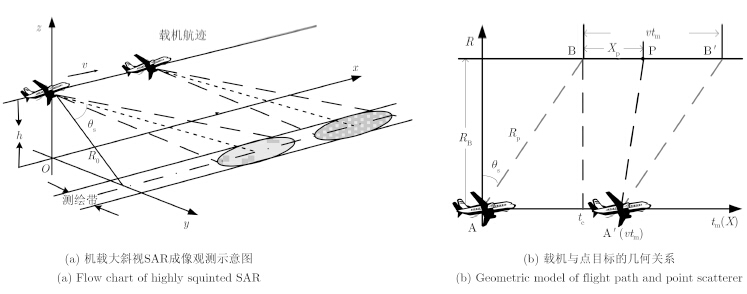
2 基于全采样数据的大斜视SAR成像算法 2.1 大斜视 SAR回波信号模型

机载SAR大斜视成像系统与观测场景之间的相对位置关系如图 1所示，雷达工作在条带模式，载机的飞行高度为h，飞行速度为v，波束射线指向的斜视角为${\theta _s}$,R₀为观测场景的中心与载机航线的最近距离。

载机飞行航线与目标构成的2维几何平面如图 1所示，点目标P离飞行航线的最近距离为R_B。设以载机位于A点时的时刻为方位慢时间的起点，这时波束中心射线与通过P点而与航线平行的线相交于B点，等效的B点同样为方位慢时间的起点，其与载机雷达的距离为R_p。雷达发射信号为LFM信号，其表达式为：

$s\left( {\hat t,{t_{\rm{m}}}} \right) = {\rm{rect}}\left( {\frac{{\hat t}}{{{T_{\rm{p}}}}}} \right)\exp \left[{{\rm{j2π }}{f_0}t + {\rm{jπ}}\gamma {{\hat t}^2}} \right]$

(1)

其中，当 $ - 1/2 \le t \le 1/2$时，${\rm{rect}}\left( t \right) = 1$,$ \gamma $为调频率，T_p为发射脉冲宽度，PRF为脉冲重复频率，${f_0}$为载频，t为全时间，$\hat t = t - {t_{\rm{m}}}$为快时间，${t_{\rm{m}}}$为慢时间。经过${t_{\rm{m}}}$后，载机飞行至 ${\rm{A'}}$，那么雷达接收到的基频回波信号为：

$\begin{aligned} s_{\rm{r}}\left( {\hat t,{t_{\rm{m}}};{R_{\rm{p}}}} \right) = & {\rm{rect}}\left( {\frac{{\hat t - {{2R({t_{\rm{m}}};{R_{\rm{p}}})} \mathord{\left/ {\vphantom {{2R({t_{\rm{m}}};{R_{\rm{p}}})} {\rm{c}}}} \right. } {\rm{c}}}}}{{{T_{\rm{p}}}}}} \right)\ \\ & \cdot {\rm \exp} \left[{{\rm{jπ }}\gamma {{\left( {\hat t - \frac{{{\rm{2}}R{\rm{(}}{t_{\rm{m}}}{\rm{;}}{R_{\rm{p}}}{\rm{)}}}}{{\rm{c}}}} \right)}^2}} \right] \\ & \cdot \exp \left[{{\rm{ - j}}\frac{{4π R({t_{\rm{m}}};{R_{\rm{p}}})}}\lambda} \right] \end{aligned}$

(2)

其中，$R({t_{\rm{m}}};{R_{\rm{p}}})$为${t_{\rm{m}}}$时刻载机与点目标P的瞬时斜距，其表达式为：

$R({t_{\rm{m}}};{R_{\rm{p}}}) = \!\! \sqrt {R_{\rm{p}}^2 \!\! + \!\! {{(v{t_{\rm{m}}} \!\! -\! \! {X_{\rm{p}}})}^2} \!\! - \!\! 2{R_{\rm{p}}}(v{t_{\rm{m}}} \!\! - \!\! {X_{\rm{p}}})\sin {\theta _s}}$

(3)

对$R({t_{\rm{m}}};{R_{\rm{p}}})$进行泰勒级数展开，由于$(v{t_{\rm{m}}} - {X_{\rm{p}}}) \ll {R_{\rm{p}}}$，因此只保留$(v{t_{\rm{m}}} - {X_{\rm{p}}})$2次以下的项，忽略高次项，得到

$\begin{aligned}R({t_{\rm{m}}};{R_{\rm{p}}}) = & {R_{\rm{p}}} \!\! - \!\! (v{t_{\rm{m}}} \!\! - \!\! {X_{\rm{p}}})\sin {\theta _s} + \frac{{{{(v{t_{\rm{m}}} \!\! - \!\! {X_{\rm{p}}})}^2}{{\cos }^2}{\theta _s}}}{{2{R_{ \rm{p}}}}}\\ = & \!\! \sqrt {R_{\rm{p}}^2 \!\! + \!\! {{\cos }^2}{ \theta _s}{{(v{t_{\rm{m}}} \!\! - \!\! {X_{\rm{p}}})}^2}} \!\! \! - \!\! (v{t_{\rm{m}}} \!\! - \!\! {X_{\rm{p}}})\sin {\theta _s} \hspace{20pt} \end{aligned}$

(4)

2.2 基于走动校正的NCS成像算法

为了便于后续分析，本部分首先给出一种基于走动校正的NCS成像算法用以处理全采样回波数据的大斜视SAR成像。将接收到的基频回波信号${s_{\rm{r}}}\left( {\hat t,{t_{\rm{m}}};{R_{\rm{p}}}} \right)$从$\hat t - {t_{\rm{m}}}$域变换到$\,{f_{\rm{r}}} - {t_{\rm{m}}}$域，得到

$\begin{aligned}{S_{\rm{r}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}};{R_{\rm{p}}}} \right) = & \exp \left( { - {\rm{jπ }}\frac{{f_{\rm{r}}^2}}{\gamma }} \right)\\ & \! \! \cdot \exp \left( { - {\rm{j}}\frac{{4πR({t_{\rm{m}}};{R_{\rm{p}}})({f_{\rm{r}}} + {f_0})}}{{\rm{c}}}} \right)\end{aligned}$

(5)

将式(4)中展开的$R({t_{\rm{m}}};{R_{\rm{p}}})$代入到式(5)，可得

$\begin{aligned} {S_{\rm{r}}} & \left( {{f_{\rm{r}}},{t_{\rm{m}}};{R_{\rm{p}}}} \right)\\ & = \exp \left( { - {\rm{j}}\frac{{4π{X_{\rm{p}}}\sin {\theta_s}({f_{\rm{r}}} + {f_0})}}{{\rm{c}}}} \right)\\ & \quad \cdot \exp \left( {{\rm{j}}\frac{{4πv{t_{\rm{m}}}\sin {\theta _s}({f_{\rm{r}}} + {f_0})}}{{\rm{c}}}} \right) \cdot \exp \left( { - {\rm{jπ }}\frac{{f_{\rm{r}}^2}}{\gamma }} \right) \\ & \quad \cdot \exp \left( { - {\rm{j}}\frac{{4π\sqrt {R_{\rm{p}}^2 + {{\cos }^2}{\theta}(v{t_{\rm{m}}} - {X_{\rm{p}}})} ({f_{\rm{r}}} + {f_0})}}{{\rm{c}}}} \right) \end{aligned}$

(6)

从式(6)可以看出，${S_{\rm{r}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}};{R_{\rm{p}}}} \right)$的第2个指数项为线性距离走动项。因此，首先补偿掉该项，构造的走动补偿函数 ${H_1}\left( {f_{\rm{r}}},{t_{\rm{m}}} \right)$为：

${H_1}\left( {{f_{\rm{r}}},{t_{\rm{m}}}} \right) = \exp \left( { - {\rm{j}}\frac{{4πv{t_{\rm{m}}}\sin {\theta _s}({f_{\rm{r}}} + {f_0})}}{{\rm{c}}}} \right)$

(7)

对补偿后的结果进行方位向的傅里叶变换，得到信号的2维频域表达式为：

$\begin{aligned} S\left( {{f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}}} \right) = & \exp \left( { - {\rm{jπ }}\frac{{f_{\rm{r}}^2}}{\gamma }} \right) \\ & \! \! \cdot \exp \left( { - {\rm{j}}\frac{{4π({X_{\rm{p}}}\sin {\theta _s})({f_{\rm{r}}} + {f_0})}}{{\rm{c}}}} \right) \\ & \! \! \cdot \exp \left( { - {\rm{j}}2π{f_{\rm{a}}}\frac{{{X_{\rm{p}}}}}{v}} \right) \exp \left( {{\rm{j}}{Ξ} ({f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}})} \right) \end{aligned}$

(8)

其中，

${Ξ} ({f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}}) \! = \! - \frac{{4π{R_{\rm{p}}}{f_0}}}{{\rm{c}}}\sqrt {{{\left( {1 + \frac{{{f_{\rm{r}}}}}{{{f_{\rm{a}}}}}} \right)}^2} - {{\left( {\frac{{{f_{\rm{a}}}\lambda }}{{2v\cos {\theta _s}}}} \right)}^2}}$

可以看出，${Ξ} ({f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}})$为距离频域${f_{\rm{r}}}$和方位频域${f_{\rm{a}}}$的耦合项，并且随着距离变化而变化。要想获得聚焦性较好的成像结果需要对其精确匹配。对 ${Ξ} ({f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}})$进行关于${f_{\rm{r}}}$的泰勒级数展开，可以得到：

$\begin{aligned}{Ξ} ({f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}}) = & {\phi _0}({f_{\rm{a}}}) + {\phi _1}({f_{\rm{a}}}){f_{\rm{r}}} + {\phi _2}({f_{\rm{a}}})f_{\rm{r}}^2 \\ & + {\phi _3}({f_{\rm{a}}})f_{\rm{r}}^3 + O({f_{\rm{a}}},f_{\rm{r}}^4)\end{aligned}$

(9)

其中，

$\begin{aligned} & {\phi _0}({f_{\rm{a}}}) = - \frac{{4π{R_{\rm{p}}}{f_0}}}{{\rm{c}}}{B}({f_{\rm{a}}}),\,\,\,{\phi _1}({f_{\rm{a}}}) = - \frac{{4π{R_{\rm{p}}}}}{{{\rm{c}}{B}({f_{\rm{a}}})}}\\ & {\phi _2}({f_{\rm{a}}}) = \frac{{2π{R_{\rm{p}}}}}{{{\rm{c}}f_{\rm{c}}^{}}}\frac{{1 - {{B}^2}({f_{\rm{a}}})}}{{{{B}^3}({f_{\rm{a}}})}} \\ & {\phi _3}({f_{\rm{a}}}) = - \frac{{2π{R_{\rm{p}}}}}{{{\rm{c}}f_{\rm{c}}^2}}\frac{{1 - {{B}^2}({f_{\rm{a}}})}}{{{{B}^5}({f_{\rm{a}}})}} \\ & \! { B}({f_{\rm{a}}}) = \sqrt {1 - {{\left( {\frac{{{f_{\rm{a}}}\lambda }}{{2v\cos {\theta _s}}}} \right)}^2}} \end{aligned}$

这样可以得到距离频率域信号 $S\left( {{f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}}} \right)$的调频率${γ _{\rm{e}}}\left( {{f_{\rm{a}}},{R_{\rm{p}}}} \right)$为：

$\frac{1}{{{γ _{\rm{e}}}\left( {{f_{\rm{a}}},{R_{\rm{p}}}} \right)}} = \frac{1}{γ } + \frac{{2{R_{\rm{p}}}}}{{{\rm{c}}f_{\rm{c}}^{}}}\frac{{1 - {{B}^2}({f_{\rm{a}}})}}{{{{B}^3}({f_{\rm{a}}})}}$

(10)

在进行NCS成像处理之前，首先需要滤除$S\left( {{f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}}} \right)$的3次相位项。根据上述推导，3次相位滤波函数${H_2}({f_{\rm{r}}})$为：

${H_2}({f_{\rm{r}}}) = \exp \left( { - {\rm{j}}{\phi _3}({f_{\rm{a}}})f_{\rm{r}}^3} \right)$

(11)

3次相位滤波处理之后的信号变换到多普勒频域-距离时间域，得到

$\begin{aligned} s'\left( {\hat t,{f_{\rm{a}}};{R_{\rm{p}}}} \right) = & {\rm{exp}}\left( { - {\rm{j}}\frac{{4π{X_{\rm{p}}}\sin {θ _{\rm{s}}}{f_0}}}{{\rm{c}}}} \right) \exp \left( { - {\rm{j}}2π{f_{\rm{a}}}\frac{{{X_{\rm{p}}}}}{v}} \right) \exp \left( { - {\rm{j}}\frac{{4π{R_{\rm{p}}}}}{λ}{B}({f_{\rm{a}}})} \right) \\& \cdot {\rm exp} \left( {{\rm{j}}π {γ _{\rm{e}}}{f_{\rm{a}}}{\rm{,}}{R_{\rm{p}}}{{\left( {\hat t - \frac{{2{X_{\rm{p}}}\sin {θ _{\rm{s}}}}}{{\rm{c}}} \!\! - \!\! \frac{{2{R_{\rm{p}}}}}{{\rm{c}}}\frac{1}{{{B}({f_{\rm{a}}})}}} \right)}^2}} \right) \end{aligned}$

(12)

下面进行NCS操作，主要完成以下3个步骤处理：(1)NCS操作；(2)距离压缩和徙动校正处理；(3)方位压缩与残余相位补偿。具体的补偿函数表达式如下^[16]：

NCS操作函数${H_3}(\hat t,{f_{\rm{a}}};{R_0})$为：

${H_3}(\hat t,{f_{\rm{a}}};{R_0}) = \exp \left( {{\rm{jπ }}{q_2}({f_{\rm{a}}}){{\left[{\hat t - {τ _{\rm{d}}}\left( {{f_{\rm{a}}},{R_0}} \right)} \right]}^2}} \right)$

(13)

其中，${q_2} = {γ _{\rm{e}}}\left( {{f_{\rm{a}}},{R_{\rm{p}}}} \right)\left( {{1 \mathord{\left/ {\vphantom {1 {{\rm B}({f_{\rm{a}}})}}} \right. } {{B}({f_{\rm{a}}})}} - 1} \right)$,${τ _{\rm{d}}}\left( {{f_{\rm{a}}},{R_0}} \right)$表示中心点目标的徙动轨迹。距离压缩和徙动校正处理的参考函数 ${H_4}({f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}})$为：

$\begin{aligned}{H_4}({f_{\rm{r}}},{f_{\rm{a}}};{R_{\rm{p}}}) = & \exp \left( {{\rm{j}}\frac{{4π({1 \mathord{\left/ {\vphantom {1 {{\rm B}({f_{\rm{a}}})}}} \right. } {{B}({f_{\rm{a}}})}} - 1){R_0}}}{{\rm{c}}}{f_{\rm{r}}}} \right) \\& \cdot \exp \left( {{\rm{j}}\frac{{π{B}({f_{\rm{a}}})f_{\rm{r}}^2}}{{{γ _{\rm{e}}}\left( {{f_{\rm{a}}};{R_{\rm{p}}}} \right)}}} \right)\end{aligned}$

(14)

方位压缩与残余相位补偿函数 ${H_5}\left( {{f_{\rm{a}}},Δτ ;{R_{\rm{p}}}} \right)$的表达式为：

$\begin{aligned}{H_5}({f_{\rm{a}}},Δτ ;{R_{\rm{p}}}) = & \exp \left( {{\rm{j}}\frac{{4π{R_0}}}{λ }{B}({f_{\rm{a}}})} \right) \\ \! \! \! & \cdot\exp \left( { - {\rm{j}}{M}({f_{\rm{a}}},{R_{\rm{p}}})} \right)\end{aligned}$

(15)

其中${ M}({f_{\rm{a}}},{R_{\rm{p}}}) = 4π{γ _{\rm{e}}}\left( {{f_{\rm{a}}},{R_{\rm{p}}}} \right)a\left( {{f_{\rm{a}}}} \right)\left( {a\left( {{f_{\rm{a}}}} \right) - 1} \right)\Delta \tau ^2,$ $\Delta \tau = {\tau _{\rm{d}}}\left( {{f_{\rm{a}}},{R_0}} \right) - {\tau _{\rm{d}}}\left( {{f_{\rm{a}}},{R_{\rm{p}}}} \right)$,${\tau _{\rm{d}}}\left( {{f_{\rm{a}}},{R_{\rm{p}}}} \right)$表示点目标P的徙动轨迹。最后作方位向的IDFT处理变换回方位向时域，即可完成在全采样条件下的大斜视SAR成像处理。聚焦后的目标位置在距离向和方位向都有偏移，需要进行几何形变校正。具体校正方法可参见文献^[3]，本文不再赘述。 3 基于降采样数据的大斜视SAR成像算法 3.1 大斜视SAR压缩感知重建模型

上述2.2节给出了全采样条件下大斜视SAR成像算法。但是为了有效减少大斜视SAR成像的回波数据量，降低成像系统的A/D采样率，利用低于Nyquist采样定理所要求的采样速率进行采集回波信号。对于降采样的回波数据而言，上述基于全采样数据的成像算法无法有效应用，需要考虑新的成像方法。

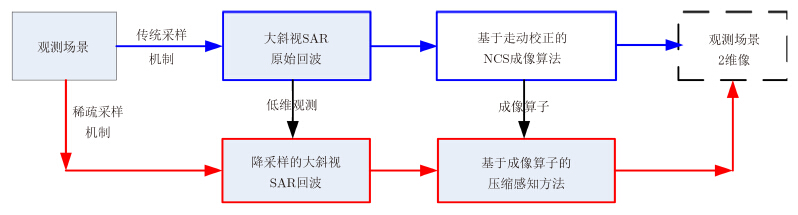
压缩感知理论能够利用信息采样代替传统的信号采样，采样速率不再由信号带宽决定，而是取决于信息在信号中的结构和内容^[17]。因此，将该理论应用于大斜视SAR成像可以以较低的采样速率完成对观测场景成像信息的采集。针对降采样数据的成像问题，首先基于2.2节提出的基于全采样数据的大斜视SAR成像算法过程构造成像算子，其次基于该成像算子构建压缩感知重构模型，通过对该重构模型的优化求解获得最终的成像结果。全采样大斜视SAR成像与降采样的大斜视SAR成像过程示意图如图 2所示。

为了便于进一步分析，首先将2.2节给出的基于走动校正的NCS成像算法写成矩阵处理形式，如下式所示：

$\begin{aligned}\Theta = & \Gamma \left( {{{s}_{\rm{r}}}} \right) \! = \! {{w} _{\rm{a}}} \cdot \left\{ \! {} \right.\left\langle \! {} \right.\left\{ \! {} \right.\left( \! {} \right.\left[{} \right.\left( {} \right.\left[{} \right.\left( {} \right. {{{\hat {w} }_{\rm{a}}} \cdot \left[{} \right.\left( {} \right.{{s}_{\rm{r}}} \cdot {{w} _{\rm{r}}}\left. {} \right) \circ {{H}_1}\left. {} \right]} \left. {} \right) \circ {{H}_2}\left. {} \right]\\ & \cdot {{\hat {w} }_{\rm{r}}}\left. {} \right) \circ {{H}_3}\left. {} \right] \cdot {{w} _{\rm{r}}}\left. {} \right) \circ {{H}_4}\left. {} \right\} \cdot {{\hat {w} }_{\rm{r}}}\left. {} \right\rangle \circ {{H}_5}\left. {} \right\} \end{aligned}$

(16)

其中，$ \circ $表示Hadamard乘积，$ {ω} $和$\hat {ω}$分别为傅里叶变换矩阵和逆傅里叶变换矩阵，下标a表示沿方位向，下标r表示沿距离向。${{s}_{\rm{r}}}$表示全采样的大斜视SAR基频回波数据矩阵，其表达式如式(2)所示，矩阵的大小为${N_{\rm{a}}} \times {N_{\rm{r}}}$ ，其中${N_{\rm{a}}}$为方位维单元数，${N_{\rm{r}}}$为距离维单元数。$\Theta$ 即为观测场景在大斜视SAR模式下的成像结果。

上述成像算法是一个可逆的过程，只要输入观测场景的复图像数据，利用该算法的逆处理即可获得原始的雷达回波数据。因此与式(16)相对应，该逆处理过程用公式表示为：

$\begin{aligned} {{s}_{\rm{r}}} = & {\Gamma ^{ - 1}}\left( \Theta \right) = \left\{ {} \right.{{w} _{\rm{a}}} \cdot \left\langle {} \right.\left[{} \right.\left( {} \right.\left( {} \right.\left( {} \right.\left( {} \right.\left( {} \right.\left( {} \right.\left( {} \right.{{\hat {w} }_{\rm{a}}} \cdot \Theta \left. {} \right) \circ {H}_5^*\left. {} \right) \cdot {{w} _{\rm{r}}}\left. {} \right)\\ & \circ {H}_4^*\left. {} \right) \cdot {{\hat {w} }_{\rm{r}}}\left. {} \right) \circ {H}_3^*\left. {} \right) \cdot {{w} _{\rm{r}}}\left. {} \right) \circ {H}_2^*\left. {} \right]\left. {} \right\rangle \left. {} \right\} \circ {H}_1^* \cdot {{\hat {w} }_{\rm{r}}} \end{aligned}$

(17)

其中，${( \cdot )^*}$表示共轭处理，s_r为原始回波数据矩阵。为了降低回波数据的A/D采样速率，本文利用随机采样方式^[18]对回波数据进行采集。该降采样方式既可以针对距离维数据也可以针对方位维数据。该采样方式的本质是利用低于Nyquist采样定理的采样速率完成对回波信号的非均匀采样。用公式描述则为构造的观测矩阵每一个列向量只有1个非零元素，并且该非零元素的值为1，位置是随机选取的。将该观测矩阵记为${Φ ^{{N_{\rm{r}}} \times {{\hat N}_{\rm{r}}}}}$，其中，${\hat N_{\rm{r}}}$为降维观测的单元数。显然利用这种方式进行数据的采集，降低了回波数据量。回波数据降采样率定义为$\eta = {{{{\hat N}_{\rm{r}}}} \mathord{\left/ {\vphantom {{{{\hat N}_{\rm{r}}}} {{N_{\rm{r}}}}}} \right. } {{N_{\rm{r}}}}}$。降采样接收回波信号的过程用公式表示为：

${{s}_{\rm{r}}}_{{\rm{com}}} = {{s}_{\rm{r}}} \cdot Φ $

(18)

进一步地，将式(17)带入式(18)，可得

${{s}_{\rm{r}}}_{{\rm{com}}} = {\Gamma ^{ - 1}}\left(\Theta \right) \cdot Φ $

(19)

因此根据压缩感知理论，通过求解下列有约束的问题即可获得观测场景的大斜视SAR成像结果 Θ：

${\rm{min}}{\left\| Θ \right\|_0},\quad {\rm{ s}}{\rm{.t}} {\rm{. }} \quad {{s}_{\rm{r}}}_{{\rm{com}}} = {\Gamma ^{ - 1}}\left( \Theta \right) \cdot Φ $

(20)

3.2 重建模型求解

为了对式(20)进行求解，将有约束的问题进一步转化为如下无约束的凸优化问题：

$\mathop {min}\limits_\Theta \frac{1}{2}\left\| {{{s}_{\rm{r}}}_{{\rm{com}}} - {\Gamma ^{ - 1}}\left( Θ \right) \cdot Φ } \right\|_2^2 + \lambda {\left\| Θ \right\|_1}$

(21)

其中，$\lambda$ 为正则化参数，用来平衡信号重构精度和信号的稀疏度。由于${\Gamma ^{ - 1}}\left( \cdot \right)$是隐性表达式，无法直接采用ITA^[19]对式(21)的凸优化问题进行求解，需要对ITA进行一定的改进。在求解的过程中，将${\Gamma ^{ - 1}}\left( \cdot \right)$计算出来的结果看作一个整体，代入到下一步的迭代中。这样就避免了传统ITA中具体的矩阵相乘要求。因此构造的迭代函数如下式所示^[14]：

${\hat Θ _k} = {\rm{soft}}\left( {{{\hat Θ }_{k - 1}} \!\! + \!\! \Gamma \left( {{{s}_{\rm{r}}}_{{\rm{com}}} \!\! - \!\! {\Gamma ^{ - 1}}\left( {{{\hat Θ }_{k - 1}}} \right) \!\! \cdot \!\! Φ } \right){Φ ^{\rm{H}}},\lambda } \right)\hspace{20pt}$

(22)

其中，${\rm{soft}}\left( {x,\lambda } \right) = {\rm{sign}}(x) \cdot \max \left( {\left| x \right| - \lambda ,0} \right)$。具体的算法流程如下：

输入 随机降采样的大斜视SAR基频回波数据s_rcom,NCS成像算子 $\Gamma \left( \cdot \right)$和其逆变换算子${\Gamma ^{ - 1}}\left( \cdot \right)$以及降采样方式决定的观测矩阵$Φ$：

输出 观测场景的大斜视SAR成像结果$Θ$。

步骤1 初始化$Θ$₀ =0，残余误差${p_0} = {{s}_{\rm{r}}}_{{\rm{com}}}$，迭代次数k=1；

步骤2 计算观测矩阵与当前残余误差的相关度，并由前次迭代的估计值估计本次的估计值，即

${{\hat \Theta }_k} = {\rm{soft(}}{{\hat \Theta }_{k - 1}} + \Gamma \left( {{p_{k - 1}} \cdot {Φ ^{\rm{H}}}} \right),\lambda {\rm{)}}$

步骤3 更新残余误差：

${p_k} = {{s}_{\rm{r}}}_{{\rm{com}}} - {\Gamma ^{ - 1}}\left( {{{\hat \Theta }_k}} \right) \cdot Φ $

步骤4 计算$\xi = {{{{\left| {{{\hat \Theta }_k} - {{\hat \Theta }_{k - 1}}} \right|}_2}} \mathord{\left/ {\vphantom {{{{\left| {{{\hat \Theta }_k} - {{\hat \Theta }_{k - 1}}} \right|}_2}} {{{\left| {{{\hat \Theta }_{k - 1}}} \right|}_2}}}} \right. } {{{\left| {{{\hat \Theta }_{k - 1}}} \right|}_2}}}$，若$\xi \le \rho $则停止迭代并输出最终的估计值${\hat \Theta _k}$，否则$k = k + 1$并转步骤2。

至此完成了基于降采样数据的大斜视SAR成像，${\hat \Theta _k}$即为获得的最终的压缩感知成像结果。

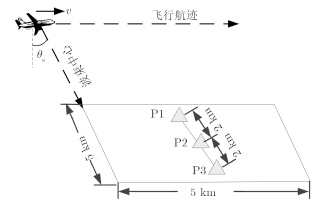
4 仿真试验 4.1 点目标仿真分析

首先采用3个点目标，分别为近距点P1，中心点P2以及远距点P3对本文2.2节提出的基于走动校正的大斜视SAR成像方法进行验证。3个点目标的布置方式以及与SAR系统的位置关系如图 3所示。SAR系统以大斜视条带模式工作，斜视角${\theta _{\rm{s}}}$为45°，中心斜距R_p为14.14 km，雷达工作在X波段(波长为0.03 m)，飞行速度v=100 m/s。观测场景的大小为5 km×5 km，其中心点与载机航迹的最近距离R₀为10 km。发射信号为LFM信号，脉冲宽度为10 μs，带宽B_a为50 MHz，获得的距离向分辨率为3 m。

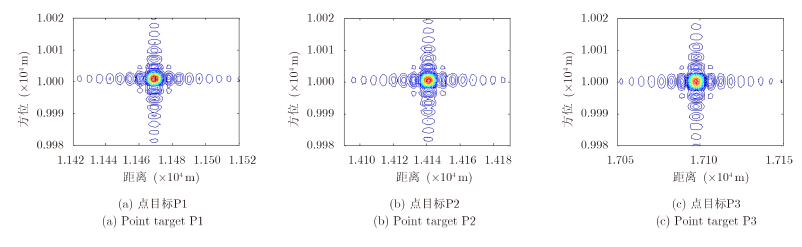
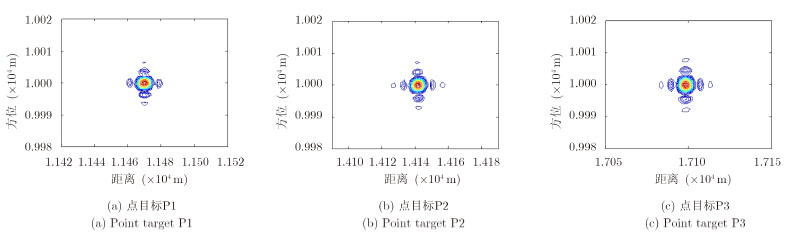
大斜视SAR回波数据在全采样条件下利用2.2节的方法得到的成像结果如图 4所示。利用随机降采样方式对回波信号进行降采样接收，降采样率$\eta$为1/3。利用所提的基于NCS算子的大斜视SAR压缩感知成像方法进行数据处理，得到的结果如图 5所示。对比图 4可以看出，基于压缩感知方法获得成像结果的旁瓣明显低于全采样成像的结果。以中心点目标P2为例，对比其峰值旁瓣比(PSLR)，可以得出全采样成像结果的PSLR是-13.4 dB，而压缩感知成像结果PSLR是-15.5 dB，低于全采样成像，说明了压缩感知成像能够降低旁瓣具有更好的聚焦能力。

4.2 面目标仿真分析

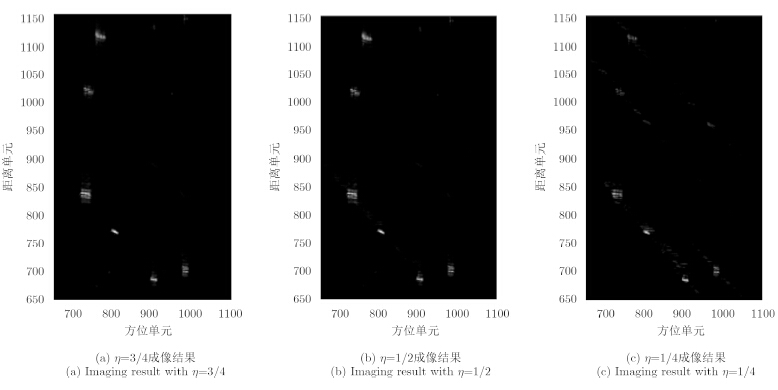
为了说明本文方法的有效性，首先对稀疏性观测场景进行成像处理。观测场景采用RADARSAT-1数据成像结果中的海湾舰船目标部分进行仿真验证，雷达系统的参数设置以及成像场景与雷达的位置关系与单点目标仿真实验一致。在回波数据全采样的条件下，利用2.2节提出的成像方法得到的成像结果如图 6(a)所示，图 6(b)是经过几何形变校正之后的结果。进一步设定大斜视SAR回波数据的采样率$\eta$分别为3/4,1/2和1/4。对于降采样的数据如果仍然采用2.2节提出的成像方法得到的结果如图 6(c)所示，可见明显具有较高的旁瓣，无法获得观测场景信息。利用第3节所提的压缩感知成像方法对降采样数据进行成像处理，得到的结果分别如图 7(a)，图 7(b)和图 7(c)所示(成像结果已完成几何形变校正处理)。可以看出图 7(a)和图 7(b)的成像结果旁瓣明显低于图 6(b)的成像结果。而图 7(c)由于降采样率$\eta$较小，重构出了部分的虚假点，但是主要的散射点不受影响，还是能够得到观测场景主要信息。

进一步利用峰值信噪比(PSNR)定量比较在不同降采样率条件下压缩感知成像质量，经计算得到图 7(a)，图 7(b)和图 7(c)的PSNR值分别为43.79 dB,41.38 dB以及37.21 dB，数值计算结果与视觉效果是一致的。均是随着$\eta$的减少成像效果逐渐变差。这与压缩感知基本理论是一致的，即观测数越少重构质量越差。

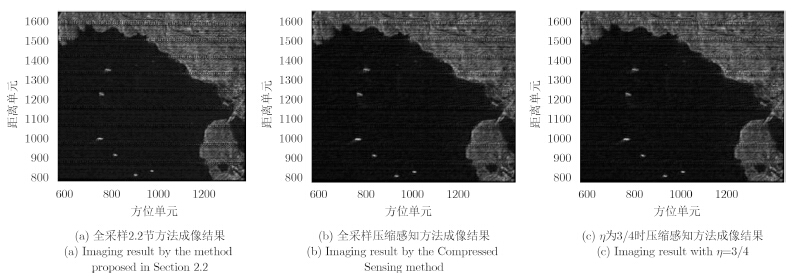
下面对非稀疏观测场景进行成像处理。观测场景采用RADARSAT-1数据成像结果中含有陆地场景部分进行仿真验证，雷达系统的参数设置以及成像场景与雷达的位置关系与上述仿真实验一致。在回波数据全采样的条件下，利用2.2节提出的成像方法和压缩感知成像方法得到的观测场景成像结果分别如图 8(a)和图 8(b)所示(成像结果已完成几何形变校正处理)。设定降采样率$\eta$为3/4，利用本文压缩感知成像方法得到的结果如图 8(c)所示，可以看出在全采样条件下两种方法均可以获得较好的成像结果，但是在降采样条件下无法获得较好的结果。说明了本文压缩感知方法在满采样的条件下能够实现对非稀疏场景的成像处理。

为了定量比较成像结果的聚焦性能，利用图像熵来定量分析。对于一副M × N的图像来说，其图像熵H定义为：

$H = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{p_{m,n}}\ln {p_{m,n}}} } ,\quad {p_{m,n}} = {{f(m,n)} \over {\sum\limits_{m = 1}^M \ \ {\sum\limits_{n = 1}^N {f(m,n)} } }}{\rm{ }}$

(23)

其中，$f(m,n)$是第$(m,n)$个像素点的像素值。经计算，图 8(a)和图 8(b)的熵值分别为5.53和5.40。可见图 8(b)的熵值小于图 8(a)的熵值，说明了利用压缩感知方法能够提高成像结果的聚焦能力，获得更高质量的成像结果。

5 结束语

本文针对大斜视SAR成像进行了研究，首先给出了全采样条件下的大斜视SAR成像算法，在此算法基础上，针对降采样数据成像问题提出一种基于NCS算子的压缩感知成像算法。通过NCS成像算子的构造以及基于该算子的压缩感知模型的构建与求解完成基于降采样数据的大斜视SAR成像处理。仿真实验验证了利用所提方法对于稀疏性成像场景能够有效降低回波数据采样率、减少数据量实现高质量成像，对于非稀疏成像场景在满采样条件下能够提高成像质量。需要说明的是，本文方法在对具有稀疏特性的SAR场景，如海洋、机场、港口等，进行成像处理时能够有效降低采样率，减少回波数据。如何利用本文方法对非稀疏的SAR场景回波数据进行压缩是下一步研究的重点。