星载SAR传感器在过去几十年中不断更新换代,实现了从无到有、从中低分辨率到高分辨率的升级,在城区复杂场景目标解译方面展现出巨大的应用潜力[1]。在高分辨率情况下,我们可获取的目标特征信息越来越丰富,其结构、形状、纹理等细节信息也更为突出;但另一方面,由于目标结构的复杂性,城区地物目标互相遮挡引起的多次散射、叠掩和阴影等现象更加明显,使得目标/场景仍然难以识别和解译[2,3]。
近年来日益得到关注的SAR层析成像(SAR Tomography,TomoSAR)技术,可以分离星载高分辨率聚束SAR数据中单个雷达分辨单元中信号混叠的多个散射体目标,准确估算各散射体的3维位置和反射量,是目前探索解决高分辨率SAR数据叠掩问题的技术手段之一[4]。真实孔径雷达层析成像始于上世纪80年代,90年代引入到SAR领域,后来有学者相继开展了仿真数据、机载SAR数据及中低分辨率星载SAR数据实验研究[5,6,7,8,9]。2007年以来,随着SAR数据分辨率的升高,城区复杂场景建筑叠掩问题突出,国内外的学者纷纷开展了高分辨率层析成像的研究[10,11,12,13]。
目前,星载SAR层析成像算法以频谱估计法为主流,其中以奇异值分解法最为经典[8,9]。然而,频谱估计法层析成像能够获得的高程向分辨率较低,与新一代高分传感器获取的方位向、斜距向分辨率不匹配。为了解决这个矛盾,近年来热门的压缩感知(Compressive Sensing,CS)技术,作为一种突破性的稀疏信号处理理论被引入SAR层析成像领域[14,15,16]。压缩感知理论能在基线数量少和分布稀疏的情况下实现高程向的高分辨率聚焦,这是基于谱估计的成像处理方法难以实现的[17,18]。由此,国内外的一系列学者也展开了相应研究。2007年,Baraniuk等人[19,20]提出可将压缩感知理论引入雷达成像中。2009年,Budillon等人[21,22]尝试用压缩感知技术进行了TomoSAR仿真实验,并于2011年将该技术应用于ERS数据TomoSAR实验。2009年,德国宇航局的Zhu等人[23,24,25,26]提出将压缩感知技术应用于高分辨率TerraSAR-X Spotlight 数据的TomoSAR实验,2011年提出了SL1MMER方法并进行了系统性的论证分析,研究结果表明了该方法独特的超分辨率优势,提取的城区高分辨率SAR数据点云精度极高。
本文将论述3维SAR层析成像的基本原理,针对传统谱估计法获得的高程向分辨率较低的问题,综述压缩感知方法在城区3维SAR层析成像中的应用,以基追踪和双步迭代收缩阈值法为例,开展TerraSAR-X聚束模式数据实验,并与传统的奇异值阈值法进行对比分析。
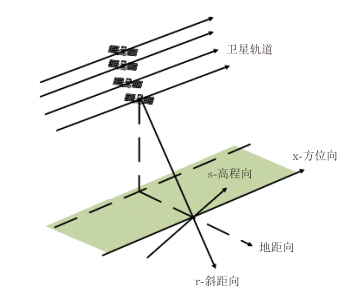
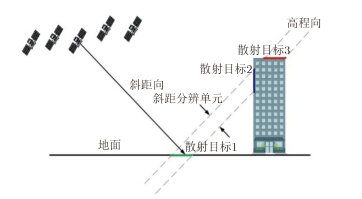
2 SAR层析成像原理一幅SAR影像的参考系为方位-斜距平面,与该平面垂直的方向称为高程向,3个方向分别用字母x,r和s表示,如图 1所示。聚焦后的SAR复数影像中,每个像素的复数值可以看作后向散射信号沿高程向的积分[9,10]。因此,每个像素的复数观测值可能来自与传感器斜距相同的多个地物目标,形成所谓的“叠掩”,如图 2所示。这种现象在高层建筑密集的城区尤为常见,为高分辨率SAR数据解译分析带来困难。目前高分辨率SAR数据的距离向和方位向分辨率可达到米级,而高程向的分辨率是未知的,需要通过SAR层析成像进行求解。SAR层析成像技术的基本目标是利用从相同轨道、相近入射角获取的N景重复轨道SAR数据重建高程向的分辨能力,分离互相叠掩的散射体。
|
图 1 SAR成像几何 Fig. 1 SAR imaging geometry |
|
图 2 城区场景SAR像元后向散射信号组成 Fig. 2 Backscattering signal of SAR pixels in typical urban scenarios |
在由N景SAR复数影像组成的数据集中,第n景影像中某个像素的复数值gn可用式(1)表示:
| $ \begin{aligned} {g_n} = & \int_{ - {s_{\max }}}^{{s_{\max }}} {\gamma (s)} \cdot \exp ( - {\rm{j}} \cdot 2{π} \cdot {\xi _n} \cdot s) {\rm{d}}s,\\ & n = 1,2,··· ,N \end{aligned}$ | (1) |
其中[-smax,smax]为信号沿高程向的分布范围;xn为高程向空间采样间隔,可由xn=-2bn/(l·r)求得;g(s)代表沿高程向分布的后向散射量。若将该函数沿高程向进行L次离散采样,且L足够大,则式(1)可离散化为
| ${{g}_{N \times 1}} = {{K}_{N \times L}} \cdot {g}_{L \times 1} + {{e} _{N \times 1}}$ | (2) |
其中,g=[g1,g2,···,gN]T是N景影像相应同一像素的复数观测值。K是一个N×L阶测量矩阵,g是后向散射强度沿高程向分布的L次离散采样,e为噪声。TomoSAR要解决的主要问题是根据数据集中相应的某一像素的N个复数观测值g,计算每个离散高程位置的后向散射量g,进而确定该像素内主导散射体的数量及每个散射体的位置,实现无模糊的3维SAR成像。
式(2)的解算方法有多种,目前以频谱估计法为主流,其中以截断奇异值分解法(Truncated Singular Value Decomposition,TSVD)最经典[9]。然而,当SAR卫星的轨道控制严格、数据集的基线跨度较短时(例如TerraSAR-X卫星),传统TSVD法可获取的高程向分辨率比方位、斜距向分辨率低了一个数量级[23,24]。在同等数据条件下,为了获取与方位-斜距方向相当的分辨率,研究具备超分辨率能力的SAR层析成像算法是十分必要的。将压缩感知理论中的信号恢复算法应用到SAR层析成像领域,可获得高程向的超分辨率。
3 压缩感知SAR层析成像压缩感知(Compressive Sensing,CS)是Donoho和Candes于2006年提出的概念,其理论包括信号稀疏表示、编码测量及重构算法3个主要方面[14,15,16]。将压缩感知理论应用到SAR层析成像也需要解决相应的3个问题,即雷达回波信号的稀疏表示、压缩感知雷达成像信号的获取及层析重构算法[13]。对于X波段高分辨率星载SAR层析成像而言,每个像素内沿高程向分布的待重建雷达信号g在空间域中是由1个或者2到3个散射中心构成,可看成是一种稀疏信号,即满足目标的稀疏性。因此,稀疏信号g可以通过L1范数最小化求解来进行重建,表示为:
| $\min {\left\| \gamma \right\|_1}s.t.g = K \cdot \gamma $ | (3) |
现有的L1最小范数求解工具箱多种多样,性能及估计精度各不相同[27]。将L1最小范数求解用于SAR层析成像的优势在于保存近似信号所需要信息的同时,尽可能地最小化信号的观测数目,可实现高程向的超分辨率。
目前压缩感知理论应用于SAR层析成像领域采用的求解方法以基追踪法(Basis Pursuit,BP)最经典[28]。基追踪法是一种全局优化算法,通过控制岭估计参数来实现真实信号与逼近信号的残差最小化。该方法由于涉及线性规划问题,计算过程耗时量大,不适合进行大面积城区场景的SAR层析成像处理。为提高SAR层析成像的处理效率,本研究小组提出采用双步迭代收缩阈值法(TWo-step Iterative Shrinkage/Thresholding,TWIST)进行SAR层析成像[29,30]。双步迭代收缩阈值法的核心思想是在迭代求解过程中,每一步迭代的结果都取决于前面两步迭代的结果,而不是仅取决于前面一步迭代的结果。该方法可使估计过程快速收敛,以牺牲少量的高程向分辨率为代价,换取计算效率大幅提高,在大面积场景处理中更加实用。
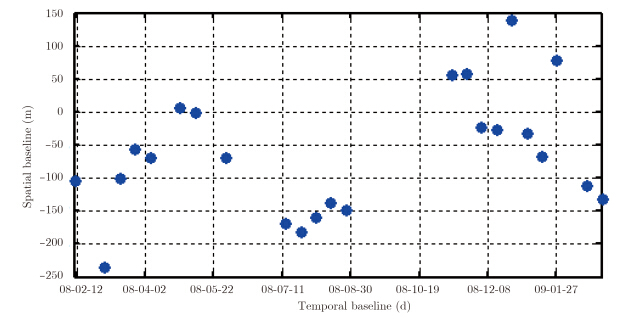
4 实验及结果分析本文使用的实验数据为2008年~2009年间获取的23景柏林市高分辨率TerraSAR-X 聚束模式上升轨道数据。该数据集的时间-垂直基线分布情况如图 3所示。作者已利用该组数据集的基线等信息开展了一系列仿真分析,仿真结果表明以BP和TWIST为代表的压缩感知法在高程向超分辨率能力、旁瓣抑制方面明显优于非压缩感知法[30]。其中,BP法的高程向超分辨率能力最强,但计算过程耗时极长;TWIST法高程向超分辨率能力稍逊于BP法,但计算效率很高,是一种兼顾计算效率与高程向超分辨率能力的方法[30]。
|
图 3 柏林实验区TerraSAR-X数据的时间-垂直基线分布情况 Fig. 3 Spatial and temporal baselines of the TerraSAR-X data stack over berlin |
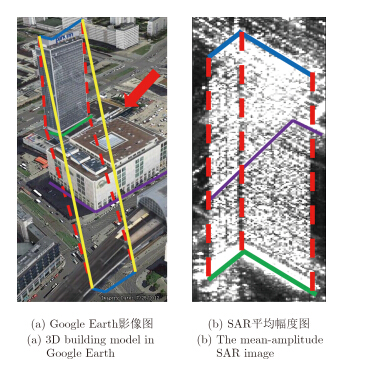
本文真实数据实验区选取在德国柏林市中心,实验对象为位于亚历山大广场西北角的Park Inn四星级酒店。该酒店共有37层,高约125 m,层高约为3.4 m,为柏林市区最高建筑。该酒店及周边环境的Google Earth影像及SAR成像几何如图 4(a)所示,其中红色箭头代表斜距方向、黄色实线为高程向。该实验对象的平均SAR幅度图如图 4(b)所示。该建筑与位于它前方的白色低矮建筑及地铁轨道发生叠掩。
|
图 4 Park Inn酒店区域的Google Earth影像图和SAR平均幅度图 Fig. 4 3D building model in Google Earth and the mean-amplitude SAR image over Park Inn |
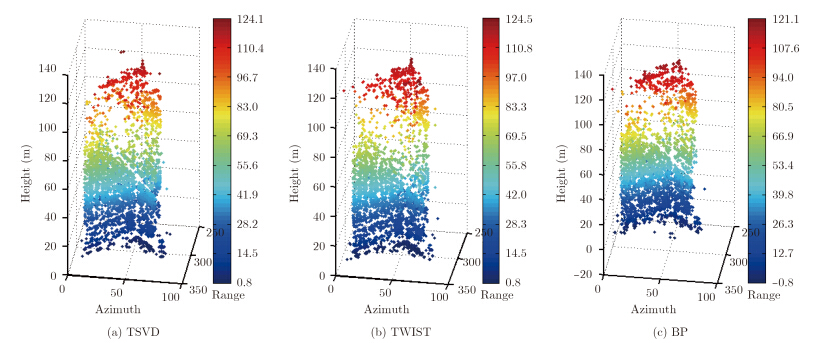
我们在该实验区提取了后向散射信号较强的3611个像元,分别用TSVD,BP和TWIST进行了层析成像分析。各方法估计出的建筑外墙面散射体分布情况相似,如图 5所示。建筑的两个外墙面形成的L形转角结构清晰可见,准确反演出了大多数散射体的高度信息。TSVD法估计出的建筑高度约为124.1 m,TWIST的估计高度约为124.5 m,BP的估计高度约为121.1 m,均与建筑实际高度125 m接近。
|
图 5 建筑墙面上的散射体分布情况 Fig. 5 Building facade scatterers detected |
3种方法分别提取出的散射体数量分布情况如图 6所示,其中红,蓝,黑分别代表 1,2,3及以上散射体。由于建筑墙面与地面形成了典型的二面角结构,墙面与地面上存在与卫星距离相等的地物目标。在建筑底部,TSVD法检测到的大部分像元为单散射体像元,这是由于TSVD法不具备高程向超分辨率能力造成的,如图 6(a)所示。而BP法和TWIST法由于具备超分辨率能力,仍可分离位于建筑底部的叠掩散射体。随着高度的攀升,地面散射体与墙面散射体之间的距离逐渐增大,TSVD便可成功分离这两种散射体,得到的层析结果与TWIST法和BP法相似。在Park Inn与前面低矮建筑发生叠掩的区域,层析结果中检测出的存在3个以上散射体的像元数量增多,这是由于该区域的散射信号可能来自于Park Inn墙面、地面、白色低矮建筑屋顶、白色低矮建筑墙面等多个部分。因此,3种方法在该区域均检测到大量的3个以上散射体像元。在图 6的左侧,3种方法均检测到了大量的单散射体像元,这是来自地铁轨道的散射信号,没有与其他建筑目标产生叠掩。

|
图 6 检测出的散射体数量分布情况 Fig. 6 Number of scatterers inside each pixel detected |
在开展该实验区的层析成像分析过程中,我们对TSVD,TWIST和BP 3种方法的计算时间进行了统计。其中,TSVD处理3611个像元用时约85 s,TWIST用时约89 s,BP用时约1378 s。在真实数据处理实验中,TWIST法与TSVD法接近,BP法耗时约为TSVD法的16倍、TWIST的15倍。TWIST法所耗时间和TSVD方法相接近,BP法虽然高程向超分辨率能力极强,但耗时最长。
上述实验结果表明:基追踪法的计算效率低下,然高程向超分辨率能力极强,适用于对计算效率要求较低、对高程向分辨率要求较高的小区域场景分析;双步迭代收缩阈值法的计算效率较高、高程向超分辨率能力弱于基追踪法,适用于对计算效率要求较高、对高程向分辨率要求较低的大区域场景分析。两种方法的超分辨率系数及散射体定位精度不是一个固定值,而是与信噪比、影像数量、各散射体的幅度、相位等诸多参数有关[25]。总体而言,两者相对于传统的谱估计法都表现出明显的高程向超分辨率优势,证明了压缩感知技术在城区SAR层析成像中的应用潜力巨大,尤其适用于高分辨率SAR层析成像。
5 结束语本文论述了3维SAR层析成像的基本原理,针对传统谱估计法获得的高程向分辨率较低的问题,综述了压缩感知方法在城区3维SAR层析成像中的应用,以基追踪和双步迭代收缩阈值法为例,开展了TerraSAR-X聚束模式数据实验,并与传统的奇异值阈值法进行了对比分析。本文的研究结果表明,压缩感知技术在高程向超分辨率、旁瓣抑制方面明显优于传统奇异值阈值法,在城区高分辨率SAR层析成像中具有广阔的应用前景。
致谢 本文作者感谢德国慕尼黑工业大学朱晓香博士在研究工作过程中给予的慷慨指导,感谢荷兰Delft理工大学Ramon Hanssen教授在学术交流过程中提供的宝贵意见。
| [1] |
郭华东, 李新武. 新一代SAR对地观测技术特点与应用拓展[J].科学通报, 2011, 56(15): 1155–1168.Guo Hua-dong and Li Xin-wu. Characteristics andapplication development of the new generation SARtechnology in earth observation[J]. Chinese Science Bulletin,2011, 56(15): 1155–1168. ( 1) 1)
|
| [2] |
张风丽, 邵芸. 城市目标高分辨率SAR遥感监测技术研究进展[J]. 遥感技术与应用, 2010, 25(3): 415–422.Zhang Feng-li and Shao Yun. Urban target monitoringusing high resolution SAR data[J]. Remote SensingTechnology and Application, 2010, 25(3): 415–422. ( 1) 1)
|
| [3] |
魏恋欢, 廖明生, Balz T, et al.高分辨率SAR层析成像建筑物叠掩散射体提取[J]. 武汉大学学报( 信息科学版), 2014,39(5): 536–540.Wei Lian-huan, Liao Ming-sheng, Balz T, et al.Layoverbuilding scatterers extraction via high resolution SARtechnology[J]. Geomatics and Information Science ofWuhan University, 2014, 39(5): 536–540.( 1) 1)
|
| [4] |
廖明生, 魏恋欢, Balz T, et al.TomoSAR技术在城市形变监测中的应用[J]. 上海国土资源, 2013, 34(4): 7–16.Liao Ming-sheng and Wei Lian-huan, Balz T, et al..Application of TomoSAR in urban deformationsurveillance[J]. Shanghai Land & Resource, 2013, 34(4): 7–16. ( 1) 1)
|
| [5] |
Chan C K and Farhat N H. Frequency swept tomographicimaging of three-dimensional perfectly conducting objects[J].IEEE Transactions on Antennas and Propagation, 1981,29(2): 312–319. ( 1) 1)
|
| [6] |
Pasquali P, Pellegrini R, Prati C, et al.Combination ofinterferograms from ascending and descending orbits[C].Proceedings of IEEE International Geoscience and RemoteSensing Symposium, California, USA, 1994, 2: 733–735. ( 1) 1)
|
| [7] |
Pasquali P, Prati C, Rocca F, et al.A 3-D SAR experimentwith EMSL data[C]. Proceedings of IEEE InternationalGeoscience and Remote Sensing Symposium, Firenze, Italy,1995, 1: 784–786.( 1) 1)
|
| [8] |
Reigber A and Moreira A. First demonstration of AirborneSAR tomography using multibaseline L-Band data[J]. IEEETransactions on Geoscience and Remote Sensing, 2000,38(5): 2142–2152.( 2) 2)
|
| [9] |
Fornaro G, Serafino F, and Soldovieri F. Three-dimensionalfocusing with multipass SAR data[J]. IEEE Transactions on[10]Geoscience and Remote Sensing, 2003, 41(3): 507–517.( 4) 4)
|
| [10] |
Zhu X and Bamler R. Very high resolution spaceborne SARtomography in urban environment[J]. IEEE Transactionson Geoscience and Remote Sensing , 2010, 48(12):4296–4308.( 2) 2)
|
| [11] |
Reale D, Fornaro G, Pauciullo A, et al.Extension of 4-DSAR imaging to the monitoring of thermally dilatingscatterers[J]. IEEE Transactions on Geoscience and RemoteSensing, 2013, 51(12): 5296–5306. ( 1) 1)
|
| [12] |
Fornaro G, Pauciullo A, Reale D, et al.Multilook SARTomography for 3-D reconstruction and monitoring of singlestructures applied to COSMO-SKYMED data[J]. IEEEJournal of Selected Topics in Applied Earth Observationsand Remote Sensing, 2014, 7(7): 2776–2785.( 1) 1)
|
| [13] |
刘康, 廖明生, Balz T. 利用压缩感知方法的高分辨率三维层析SAR研究[J]. 武汉大学学报(信息科学版), 2012, 37(12):1456–1459. Liu Kang, Liao Ming-sheng, and Balz T. High resolution 3Dtomographic SAR with compressive sensing[J]. Geomaticsand Information Science of Wuhan University, 2012, 37(12):1456–1459.. (  2) 2)
|
| [14] |
Donoho D L. Compressed sensing[J]. IEEE Transactions onInformation Theory, 2006, 52(4): 1289–1306 ( 2) 2)
|
| [15] |
Candés E J, RombergJ, Tao T, et al.Robust uncertaintyprinciples: exact signal reconstruction from highlyincomplete frequency information[J]. IEEE Transactions onInformation Theory, 2006, 52(2): 489–509. ( 2) 2)
|
| [16] |
Candès E J. Compressive sampling[J]. Marta Sanz Solé,2007: 1433–1452. ( 2) 2)
|
| [17] |
吴一戎, 洪文, 张冰尘, 等. 稀疏微波成像研究进展(科普类)[J].雷达学报, 2014, 4(4): 383–395.Wu Yi-rong, Hong Wen, Zhang Bing-chen, et al.Currentdevelopments of sparse microwave imaging[J]. Journal ofRadars, 2014, 4(4): 383–395. ( 1) 1)
|
| [18] |
闵锐, 杨倩倩, 皮亦鸣, 等. 基于正则化正交匹配追踪的SAR层析成像[J]. 电子测量与仪器学报, 2012, 26(12): 1069–1073.Min Rui, Yang Qian-qian, Pi Yi-ming, et al.SARtomography imaging based on regularized orthogonalmatching pursuit[J]. Journal of Electronic Measurement andInstrumentation, 2012, 26(12): 1069–1073. ( 1) 1)
|
| [19] |
Baraniuk R and Steeghs P. Compressive radar imaging[C].IEEE Radar Conference, Boston, USA, 2007: 128–133.( 1) 1)
|
| [20] |
Baraniuk R. Compressive sensing[J].IEEE SignalProcessing Magazine, 2007: 118–121. ( 1) 1)
|
| [21] |
Budillon A, Evangelista A, Schirinzi G, et al.SARtomography from sparse samples[C]. IEEE InternationalGeoscience and Remote Sensing Symposium (IGARSS),Cape Town, 2009, 4: 865–868. ( 1) 1)
|
| [22] |
Budillon A, Evangelista A, Schirinzi G, et al.Threedimensional SAR focusing from multipass signals usingcompressive sampling[J]. IEEE Transactions on Geoscienceand Remote Sensing, 2011, 49(1): 488–499. ( 1) 1)
|
| [23] |
Zhu X and Bamler R. Very high resolution SARtomography via Compressive Sensing[C]. Proceedings ofFringe, Frascati, Italy, 2009: 1–7. ( 2) 2)
|
| [24] |
Zhu X and Bamler R. Tomographic SAR inversion by L1-norm regularization—The compressive sensing approach[J].IEEE Transactions on Geoscience and Remote Sensing,2010, 48(10): 3839–3846.( 2) 2)
|
| [25] |
Zhu X and Bamler R. Super-resolution power androbustness of compressive sensing for spectral estimationwith application to spaceborne tomographic SAR[J]. IEEETransactions on Geoscience and Remote Sensing, 2012,50(1): 247–258.( 2) 2)
|
| [26] |
Zhu X and Bamler R. Demonstration of super-resolution fortomographic SAR imaging in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012,
50(8): 3150–3157. ( 1) 1)
|
| [27] |
Michael E. Sparse and Redundant Representations: FromTheory to Applications in Signal and Image Processing[M].New York, U.S., Springer, 2010. ( 1) 1)
|
| [28] |
Chen S S, Donoho D L, and Saunders M A. Atomicdecomposition by basis pursuit[J]. SIAM Review, 2001,43(1): 129–159. ( 1) 1)
|
| [29] |
Bioucas-Dias J M and Figueiredo M A T. A new TwIST:two-step Iterative Shrinkage/Thresholding algorithms forimage restoration[J]. IEEE Transactions on ImageProcessing, 2007, 16(12): 2992–3004.( 1) 1)
|
| [29] |
Baraniuk R. Compressive sensing[J].IEEE SignalProcessing Magazine, 2007: 118–121. ( 1) 1)
|
| [30] |
Wei L, Balz T, Zhang L, et al.A novel fast approach forSAR tomography: two-step iterativeshrinkage/thresholding[J]. IEEE Geoscience and RemoteSensing Letters, 2015, 12(6): 1377–1381. ( 3) 3)
|


