真弹头的有效识别是弹道导弹防御的关键,而识别所用特征又是影响识别效果的关键因素。近年来,基于微动特征的中段目标识别成为研究热点。为了使弹头再入大气层时保证一定的再攻角,弹头在中段一般通过自旋保持姿态稳定,而轻微的扰动将导致自旋目标进动,进动参数主要包括进动轴指向、进动角、进动周期。文献[1]指出,可利用进动周期与进动角计算纵横惯量比,从而对真假弹头进行有效判别。基于这一结论,近年来基于微多普勒信息的中段目标特征提取及相关技术受到了广泛的关注,发表了大量文献[2, 3]。但从已发表的文献看,绝大多数研究都是基于孤立单目标假设前提的。在实际情况中,母舱和导弹遗留下来的助推器残骸在近似真空的环境中伴随弹头惯性飞行;此外,为了提高突防概率,弹头在中段还会释放各类诱饵,从而形成包含碎片、诱饵、弹头的中段威胁目标群,当雷达照射波束内包含多个目标时,各目标回波信号在距离维、角度维可能均是不可分的。群目标中各目标回波信号在时域、频域均交织在一起,为了利用微多普勒信息提取各目标的微动特征,群目标信号分离是基本前提。
针对群目标回波信号分离问题,文献[4]采用独立成分发析技术,在接收回波路数大于或等于目标数目时实现了中段群目标信号分离;文献[5]对上述方法进行了改进,将欠定盲源分离方法引入到群目标微多普勒信号分离中,从少数原始混叠回波中分离出了多个目标的微多普勒信号。但上述方法所要求的最少回波路数为3。在实际应用中,由于观测条件有限,往往难以形成多路观测信号,此时,上述方法将不再适用。
本文对基于单路回波信号的群目标信号分离方法展开研究,提出了基于时频域联合滤波的群目标回波信号分离方法。该方法首先对回波中的微动周期进行估计,然后根据微动的周期特性通过信号的分段处理得到对应微动周期目标的回波信号。最后给出了微动信号分离的仿真结果,验证了算法的有效性。
2 中段群目标微动模型中段目标运动包含了沿弹道的平动和绕质心的微动。平动补偿是微多普勒特征分析的前提。针对平动补偿问题已有较多文献进行了研究,为了描述简单,本文假设中段目标的平动已完全补偿。
中段目标的微动主要包含了弹头的进动及碎片的翻滚。碎片的翻滚是绕质心旋转与质心沿弹道平动的结合,在平动补偿后仅保留了旋转微动。对于旋转目标而言,目标上等效散射中心的运动模型可用下式描述:
| ${r_{{\rm{r}}m}}(t) = {x_{{\rm{r}}m}}\cos \left( {{{ω} _{\rm{r}}}t + {{\varphi} _{\rm{r}}}} \right) + {y_{{\rm{r}}m}}\sin \left( {{{ω} _{\rm{r}}}t + {{\varphi} _{\rm{r}}}} \right)$ | (1) |
为了保证弹头再入大气层的再攻角,弹头通过自旋保持指向,而诱饵释放过程中的扰动将使得自旋目标进动。弹头目标的结构一般是类锥形的,具有旋转对称特性。旋转对称目标的散射特性只和入射方向与对称轴的夹角有关[6]。此时,弹头进动所导致的等效散射中心运动可用下述模型描述[6]:
| ${r_{{\rm{p}}m}}(t) = {x_{{\rm{p}}m}}\cos {β} (t) + {y_{{\rm{p}}m}}\sin {β} (t)$ | (2) |
| ${β} (t) = {\rm{acos}}\left( {\cos {\gamma} \cos {{\theta} _{\rm{P}}} \! + \! \sin {\gamma} \sin {{\theta} _{\rm{P}}}\cos ({{w} _{\rm{P}}}t \! + \! {{\varphi} _{\rm{P}}})} \right)$ | (3) |
当群目标中多个目标之间距离间隔较小,不满足距离可分辨条件时,平动补偿后群目标所在距离门的回波信号可表示为:
| $s(t) = \sum\limits_{n = 1}^N {{s_n}(t)} \hspace{100pt}$ | (4) |
| ${s_n}(t) = \sum\limits_m^{} {{\sigma _{nm}}\exp \Bigg\{ - {\rm{j}}\frac{{4{π}{f \! _c}}}{{\rm{c}}}{r_{nm}}(t) \Bigg\}}$ | (5) |
对中段群目标而言,若需要提取某个目标的微动参数,首先要对群目标回波信号进行分离,得到单个目标回波信号。式(5)表明群目标回波信号在时域完全混叠,在频域上各目标频率变化均具有周期性特点且中心频率均为零频,难以单独从时域或频域对回波进行分离。
3 基于时频域滤波的群目标信号分离中段目标的微动具有周期性,微动的周期性对应了回波变化的周期性,且不同目标所对应的微动周期不一致。因此,可首先估计出某个目标的微动周期,然后对回波信号进行分段,分段后对应周期目标信号在每一段中重复出现而其它目标信号不具有此特性,从而可通过对多段信号的分析提取出具有对应周期的信号分量。
3.1 微动周期估计微动周期是微动目标的重要参数,基于回波序列的微动周期估计方法主要有自相关法、平均幅度差函数法等,其中自相关法抗噪性能好,物理意义明确,广泛应用于中段目标微动周期估计。基于自相关法的微动周期估计表达式为[7]:
| $\hat T = \arg \mathop {\max }\limits_{{T_{\min }} < \tau \le {\rm{Tmax }}} \int {{\rm{s}}({\rm{t}}){{\rm{s}}^{\rm{*}}}({\rm{t + }}\tau ){\rm{dt}}} $ | (6) |
根据估计出的某一个周期T将回波序列以T为周期划分为多个时间段并进行时频分析。对周期恰好为T的信号分量而言,在各时间段内其对应回波信号在时频面上所对应的强能量区域是一致的,而周期不为T的信号分量不具有此特性。因此,可通过对多个周期信号的时频分析结果提取出周期T的信号分量在时频面上的支撑域,从而进一步根据支撑域对回波信号进行时频域联合滤波得到周期为T的信号分量。所提取的信号分量可认为对应一个目标的回波信号。
对时频域联合滤波而言,由于要对信号进行逆时频变化得到滤波后信号,因此要选择存在逆变换的时频变换方法。广义S变换是一种应用广泛的时频滤波变换算法,广义S变换可表示为[8]:
| \[\begin{array}{l} S\left( {\tau ,f} \right) = \int\limits_{ - \infty }^\infty {s\left( t \right)\frac{{\lambda {{\left| f \right|}^p}}}{{\sqrt {2\pi } }}} \exp \left( {\frac{{ - {\lambda ^2}{f^{2p}}{{(\tau - t)}^2}}}{2}} \right)\\ \quad \quad \quad \quad \cdot \exp \left( { - {\rm{j}}2\pi ft} \right){\rm{d}}t \end{array}\] | (7) |
| $s\left( t \right) = \int_{ - \infty }^\infty {\left\{ {\int_{ - \infty }^\infty {S\left( {\tau ,f} \right){\rm{d}}\tau } } \right\}} \exp \left( {{\rm{j}}2π ft} \right){\rm{d}}f$ | (8) |
由于S逆变换可无误差恢复信号,因此可根据信号在时频平面上的分布特性设置滤波器对信号进行时频滤波,具体可表示为:
| ${h_x}(t) = \int_{ - \infty }^\infty { \biggr\{ \int_{ - \infty }^\infty {S(\tau ,f)F(\tau ,f){\rm{d}}\tau } \biggr\} } \exp ({\rm{j}}2{\rm{π }}ft){\rm{d}}f$ | (9) |
| $F(\tau ,f) = \left\{ {\begin{array}{*{20}{c}} \! \! {1,}\ \ {(\tau ,f) \in R}\\ \! \! {0,}\ \ {(\tau ,f) \notin R} \end{array}} \right. \hspace{95pt}$ | (10) |
对于中段群目标而言,设已估计出了某目标的周期T,对应为目标1,以T为间隔将s(t)划分为多个信号段:
| ${s_i}(t') = s(iT + t')\matrix{ {,\;} \cr } 0 \le t' \le T$ | (11) |
| ${H_{{\rm{t1}}}}(\tau ,f) = \mathop \cap \limits_i {H_{{\rm{d}}i}}(\tau ,f) \hspace{35pt}$ | (12) |
| ${H_{{\rm{d}}i}}(\tau ,f) = \left\{ {\begin{array}{*{20}{c}} \!\! 1 ,& {{S_i}(\tau ,f) \ge {g_i}}\\ \!\! 0 ,& {{S_i}(\tau ,f) \lt {g_{_i}}} \end{array}} \right.$ | (13) |
得到${H_{{\rm{t}}1}}(\tau ,f)$后,可得第i段信号内目标1对应信号分量为:
| $\begin{aligned} {s_{{\rm{1}}i}}(t') = & \int_{ - \infty }^\infty {\biggr\{ \int_{ - \infty }^\infty \!\!\! {{S_i}(\tau ,f){H_{{\rm{t1}}}}(\tau ,f){\rm{d}}\tau } \biggr\} } \\ & \cdot \exp ({\rm{j}}2π ft){\rm{d}}f \end{aligned}$ | (14) |
| ${s_1}\left( t \right) = \left[{{s_{11}}\left( {t'} \right) \ {s_{12}}\left( {t'} \right) \!\!\!\! \quad \cdots } \right]$ | (15) |
通过3.2节处理,可得到目标1回波在各采样时刻所对应信号,将原始信号减去分离出的信号,重复上述过程,可依次分离出多个目标的信号。具体步骤如下:
(1) 设剩余信号为${s_{{\rm{res}}}}(t) = s(t)$;
(2) 针对${s_{{\rm{res}}}}(t)$,根据式(6)和式(7)估计出进动周期T;
(3) 根据估计出的周期T,根据式(11)对$s(t)$进行分段,对每一段信号${s_i}(t')$进行S变换得到${S_i}(\tau ,f)$;
(4) 根据式(13)提取${S_i}(\tau ,f)$的强能量区域${H_{{\rm{d}}i}}(\tau ,f)$;根据式(12)得到目标1在时频面上所对应的支撑域${H_{{\rm{t1}}}}(\tau ,f)$;
(5) 根据式(14)得到目标i在各段对应的信号分量;进一步得到其回波信号${s_1}(t)$;
(6) sres(t)=sres(t)–s1(t),重复步骤(2)–步骤(5),直到从${s_{{\rm{res}}}}(t)$中提取的信号能量小于某一门限值。
4 仿真分析
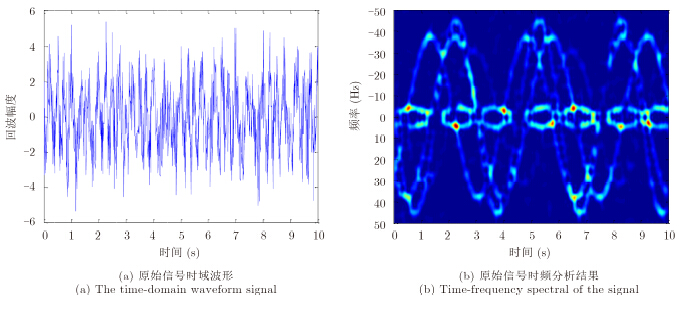
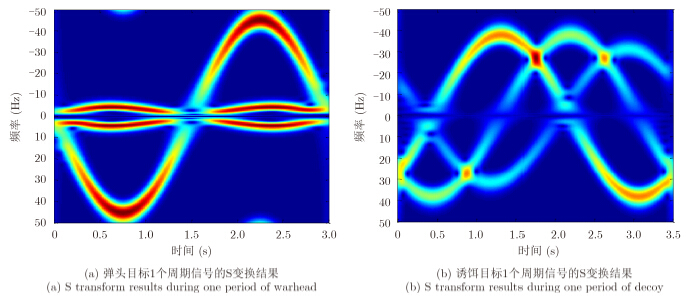
设群目标中包含2个目标,1个为进动弹头1个为翻滚诱饵。弹头包含3个散射系数均为1的等效散射中心,坐标分别为(0,3.0)、(0.5,0)、(–0.5,0);弹头进动参数如下:$γ = {60^ \circ }$,${θ _\rm{P}} = {8^ \circ }$,${ω _\rm{P}} = 2/3π$ rad/s。诱饵包含散3个等效散射中心,坐标分别为(–0.25,0.25)、(0.25,0.25)、(0.25,–0.15),散射系数分别为1.0、0.7、0.5,诱饵的旋转周期为3.5 s。雷达的中心频率为9 GHz,重复频率为100 Hz,观测时间为10 s。根据设定的点散射中心模型仿真得到回波后加入噪声到总体信噪比为10 dB,回波信号序列如图 1(a)所示。为了在时频面描述回波信号的瞬时多普勒频率,利用Margenau-Hill-Spectrogram时频变换对回波进行分析,得到时频分析结果如图 1(b)所示。从图 1可以看出,2个目标信号在时域和频域均是混叠在一起的。弹头和诱饵的理论计算信号在1个周期内的S变换结果如图 2
所示。
|
图 1 群目标回波信号 Fig.1 Radar echo of group target |
|
图 2 单个目标信号的时频分析结果 Fig.2 Time-frequency spectral of single target |
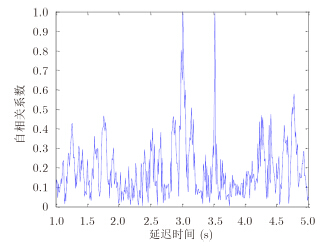
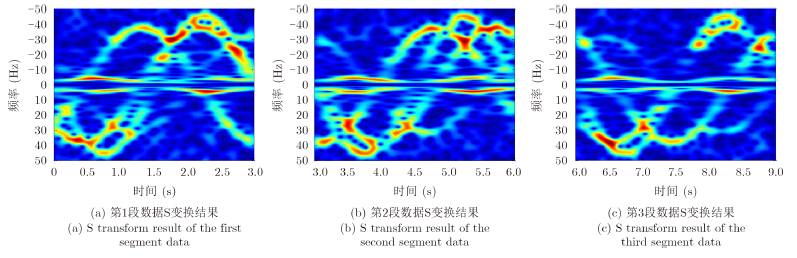
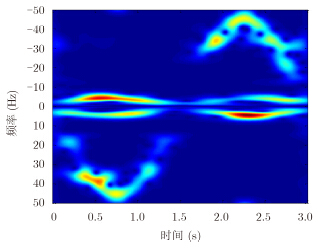
根据3.1节所描述的基于自相关函数的微动周期估计方法,得到自相关函数如图 3所示,从图可以看出,对于延迟时间为3 s时所对应的自相关系数最大,因此得到目标1的微动周期为3 s。以3 s为间隔,可将回波信号分为3段,对应观测时间为0~9 s。利用S变换对各段回波信号进行分析,得到其变换结果如图 4所示。在S变换时频图中提取各段的强能量区域,得到各段强能量区域的交集如图 5所示,此区域对应了目标1在1个周期内的信号在S变换时频面上所对应支撑域。根据图 5所示支撑域对各段信号进行时频域联合滤波,得到第1段数据滤波后信号所对应的S变换如图 6所示。从图 6可以看出,所提取信号的周期为3 s。将图 6与图 2(a)对比可知目标1对应了弹头的回波信号。将每段所提取信号与弹头点散射中心模型产生的理论回波信号进行相关处理,得到所提取3段信号与理论信号的相关系数分别为0.8686、0.8565、0.8565。
|
图 3 基于自相关处理的微动周期估计 Fig.3 Micro-motion period estimation based on autocorrelation processing |
|
图 4 各段回波信号S变换结果 Fig.4 S transform results of different segment data |
|
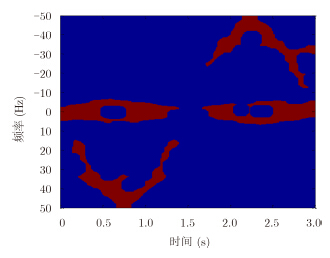
图 5 目标1在时频面上的支撑域 Fig.5 The support domain in time-frequency dimension of target1 |
|
图 6 目标1在1个周期内信号的S变换结果 Fig.6 S transform results of target1’s signal during one period |
在对目标1回波信号进行分离时,假设估计周期存在误差,对于不同的周期值,分解所得各段信号与原始信号的相关系数如表 1所示,从表可以看出,周期误差越大,提取信号与理想信号的相关度越差,当估计误差不大于1%时,对于目标1各段信号分量与原始信号的相关度变化范围不大于4%。
| 表 1 周期估计误差对算法性能的影响 Tab. 1 Algorithm performance with period estimating error |
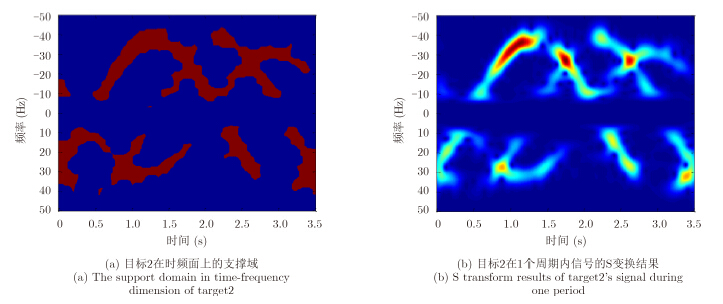
将原始信号减去各段所提取信号,可得0~9 s内的剩余信号,进一步重复上述步骤,得到目标2的微动周期为3.5 s,其在1个周期内对应的支撑域如图 7(a)所示。以3.5 s为间隔,可将回波信号分为2段,对应观测时间为0~7 s。 经过对两段回波信号的处理,最后得到目标2在1个周期的估计信号如图 7(b)所示,此目标信号对应了诱饵的回波信号。将每段所提取信号与诱饵的点散射中心模型产生的理论回波信号进行相关处理,得到所提取两段信号与理论信号的相关系数分别为0.7932、0.7706。
|
图 7 目标2信号分离结果 Fig.7 Signal separation results of target2 |
将图 6、图 7(b)与图 2进行对比分析可以发现,所提取信号的时频分析结果与理论信号的时频分析结果存在一定差异。这主要是由于本文方法是通过提取目标在时频面上的支撑域实现回波信号分离的,对两个目标信号在时频面上存在重叠的区域不能对其进一步分离,而只能将整个区域的信号判断为某个目标的回波信号。
5 讨论针对中段群目标回波信号分离问题,本文提出了基于时频域联合滤波的信号分离算法。该算法首先估计目标的微动周期,然后根据所估计周期对回波信号进行分段处理,提取各段信号 S 变换后强能量区域在时频域的交集,即对应了目标信号在时频面上的支撑域。基于该支撑域对回波进行时频滤波,可得到具有同一周期特性的回波信号,从而实现回波信号的分离。
仿真结果表明,基于时频域滤波的方法能基本实现群目标信号的分离,但分离信号与单个目标信号的相关性并不是太高(只有0.8左右),且从时频图来看分离信号的时频分布与目标理论信号的时频分布也存在差别。此外,对于仿真产生的理想目标信号而言,数据越短,所包含信号周期越少,所提取的支撑域与实际信号支撑域的差别越大,但数据越长,所提取的支撑域与目标所实际对应支撑域相似度越好,但实际中,数据越长,越难以保证信号在周期与周期之间的一致性,因此,如何实现更有效的群目标回波信号分离需要进一步深入研究。
| [1] | 刘永祥, 黎湘, 庄钊文. 空间目标进动特性及在雷达识别中的应用[J]. 自然科学进展, 2004, 14(11): 1329-1332. Li Yong-xiang, Li Xiang, and Zhuang Zhao-wen. Precession characteristics of spatial targets and applications in radar recognition[J].Progress in Natural Science, 2004, 14(11): 1329-1332.(  1) 1) |
| [2] | 姚汉英, 孙文峰, 马晓岩. 基于高分辨距离像序列的锥体目标进动和结构参数估计[J]. 电子与信息学报, 2013, 35(3): 537-543. Yao Han-ying, Sun Wen-feng, and Ma Xiao-yan. Precession and structure parameters estimation of cone-cylinder target based on the HRRPs[J].Journal of Electronics & Information Technology, 2013, 35(3): 537-543.(  1) 1) |
| [3] | 李飞, 纠博, 邵长宇, 等. 目标微动参数估计的曲线跟踪算法[J]. 电波科学学报, 2013, 28(4): 278-295. Li Fei, Jiu Bo, Shao Chang-yu, et al.. Curve tracking based parameter estimation of micro-motion[J]. Chinese Journal of Radio Science, 2013, 28(4): 278-295.(  1) 1) |
| [4] | Guo Kun-yi, Li Q, and Sheng Xin-qing. A precise recongnition method of missile warhead and decoy in multi-target scene[J]. Journal of Electromagnetic Waves and Applications, 2010, 24(516): 641-652.( 1) 1) |
| [5] | 郭琨毅, 张永丽, 盛新庆, 等. 基于欠定盲分离的多目标微多普勒特征提取[J]. 电波科学学报, 2012, 27(4): 691-695. Guo Kun-yi, Zhang Yong-li, Sheng Xin-qing, et al.. An approach for extracting independent micro-Doppler characteristics of multiple targets based on underdetermined blind source separation[J]. Chinese Journal of Radio Science, 2012, 27(4): 691-695.(  1) 1) |
| [6] | Liu Yong-xiang, Li Xiang, and Zhuang Zhao-wen. Estimation of micro-motion parameters based on micro-Doppler[J]. IET Signal Processing, 2010, 4(3): 213-217.( 2) 2) |
| [7] | 肖立, 周剑雄, 何峻, 等. 弹道中段目标进动周期估计的改进自相关法[J]. 航空学报, 2010, 31(4): 812-818. Xiao Li, Zhou Jian-xiong, He Jun, et al.. Improved autocorrelation method for precession period estimation of ballistic target in midcourse[J].Acta Aeronautica et Astronautica Sinica, 2010, 31(4): 812-818.(  2) 2) |
| [8] | 陈学华, 贺振华, 黄德济. 广义S变换及其时频滤波[J]. 信号处理, 2008, 24(1): 28-31. Chen Xue-hua, He Zhen-hua, and Huang De-ji. Generalized S transform and its time-frequency filtering[J]. Signal Processing, 2008, 24(1): 28-31.(  1) 1) |
 2015
2015
