② 中国科学院大学 北京 100049;
③ 内蒙古工业大学雷达技术研究所 呼和浩特 010051
② University of Chinese Academy of Sciences, Beijing, 100049, China;
③ Radar Research Institute, Inner Mongolia University of Technology, Hohhot, 010051, China
平流层飞艇因其在高空可驻留的特点,在高空侦察、区域预警和通信服务等领域有着广阔的应用前景[1]。平流层飞艇巨大的体积为使用大尺寸天线实现实孔径成像提供了条件,但是大尺寸天线需要大量的子阵单元和接收通道,同时天线波束还需要扫描以扩大观测范围,因而使得雷达系统的体积重量和复杂度均大大增加。采用具有稀疏特点的综合孔径天线有可能解决上述问题[2]。
然而,稀疏阵列的非均匀采样会引起高的副瓣和栅瓣,降低图像质量。压缩感知(CompressedSensing,CS)理论提供了一种对稀疏信号在较少采样下进行重建的方法[3, 4],该方法在满足一定使用条件下可有效地抑制副瓣和栅瓣。
自从CS理论被引入雷达成像领域以来,相关的研究工作取得了很多进展[5, 6, 7, 8, 9],如文献[5]提出了对共形稀疏阵天线利用CS理论进行运动目标图像重建的方法,文献[6]研究了基于CS的城区场景高度维重建方法。但上述文献的研究内容大多为空间稀疏的场景,如海面舰船,空中的飞行器等。实际应用中,空间场景大多是非稀疏的。对此,需要研究变换域稀疏条件下的对地成像问题,例如文献[9]研究了变换域稀疏的侧视3维成像。但基于变换域稀疏的工作仍然研究的不多,需要进一步深入。
本文针对飞艇平台,设计了基于组合巴克码的共形稀疏阵列,分析了其探测性能。在对地成像时,利用两次脉冲的实孔径成像的结果,可去除散射单元的随机初相位,使场景在变换域稀疏。从而可以使用CS方法,在稀疏阵列条件下完成对地成像。 2 阵型设计和性能分析
针对飞艇平台具有较大体积,可布设较大尺寸天线的特点,本节采用了组合巴克码序列,设计了对应的共形稀疏阵列,并对其探测性能进行了分析。 2.1 组合巴克码阵列
巴克码是一种具有良好相关特性的二相码序列,它具有一定的稀疏性,有助于稀疏重建。但巴克码的码长较短,最长只有13位,以其序列形式排布的阵列与飞艇平台不匹配,故考虑采用相关特性略差但码长较长的组合巴克码序列排布稀疏阵列。
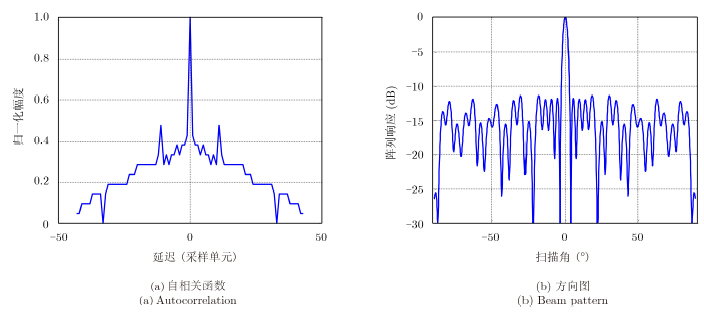
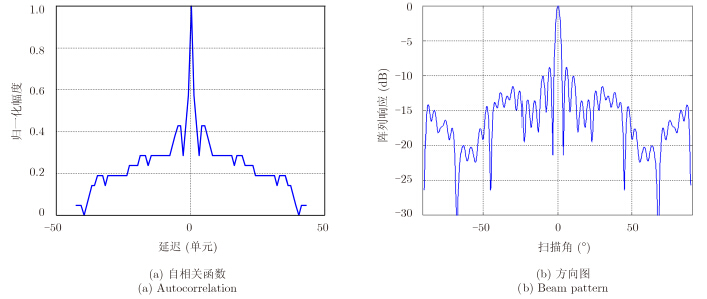
组合巴克码的由两组巴克码联合生成[10]。综合考虑阵列长度和稀疏率,本文采用由4位巴克码[1110]和11位巴克码[11100010010]构成的44位组合巴克码序列。该序列共有2种形式,第1种是以4位巴克码序列作为11位巴克码的码元(4×11),第2种是以11位巴克码序列作为4位巴克码的码元(11×4),其编码序列分别为[11100010010111000100101110001001000011101101]和[1110111011100001000100011110000100011110000]。这两种编码方法所得组合巴克码序列长度均为44,均有21个阵元,稀疏率约50%,但其自相关序列有所不同,其自相关函数和对应的阵列方向图见图 1和图 2。
|
图 1 44位组合巴克码自相关与方向图情况(4×11) Fig.1 Autocorrelation and beam pattern of 44 bit combined Barker code(4×11) |
|
图 2 44位巴克码自相关与方向图情况(11×4) Fig.2 Autocorrelation and beam pattern of 44 bits combined Barker code(11×4) |
由图 1(b)可知,第1种巴克码峰值旁瓣比(Peak to Side-Lobe Ratio,PSLR)较低,达-11.82dB。但图 1(a)中±11延迟处的尖峰和图 1(b)反映出该序列远区副瓣较高。而第2种虽然PSLR相对较高(-8.80dB),但远区副瓣较低,更适于对地成像。综合以上分析,本文阵采用11×4形式的44位组合巴克码作为稀疏阵列的排布方式。需要说明的是,本文的阵列相对于文献[2]中的稀疏阵列稀疏率较低,但旁瓣栅瓣情况较好,可在不换取等效满阵的情况下对地成像。 2.2 稀疏阵列信噪比分析
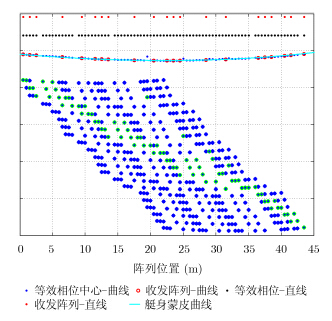
将上述44位巴克码排布的稀疏阵列子阵在直线上的位置(图 3中红色点),分别投影到三叶玫瑰线(蓝色曲线)上,来获得与艇身底部共形的稀疏阵列,根据等效相位中心原则,可获取21组等效相位中心(蓝色点)。天线布局(红色圆点)[5]根据路径差最小的原则,选取对应的等效相位中心(绿色圆点),形成孔径综合后的阵列。其投影方式和阵列布局情况如图 3所示。
|
图 3 天线阵列和等效相位中心位置 Fig.3 The position of antenna arrays and effective phase centers |
传统意义上的密集阵列天线雷达的作用距离分析和计算方法较为成熟,由于天线阵列的布设方式不同,需对稀疏阵列天线雷达的性能进行分析。本节采用文献[11]中的方法对稀疏阵列天线雷达的对地面运动目标探测和实孔径成像的性能进行了分析。稀疏阵列天线雷达系统每个子阵长1m,全阵可达44m。详细的雷达系统参数见表 1。
| 表 1 系统参数 Tab. 1 System parameters |
要获得良好的运动目标检测性能和成像质量,信噪比是非常重要的一项指标。根据雷达方程,单脉冲信噪比公式可表示为:
| ${\rm{SNR = }}{{{P_t}\sigma A_{\rm{e}}^{\rm{2}}\tau } \over {{\rm{4}}\pi {R^{\rm{4}}}{\lambda ^{\rm{2}}}Lk{T_s}{F_n}}}$ | (1) |
| ${\rm{SN}}{{\rm{R}}_{\rm{2}}} = {\rm{SN}}{{\rm{R}}_{\rm{1}}} + 13:2 = 1:92 \rm{(dB)}$ | (2) |
当使用21个子阵同时发射和接收信号时,等效阵列长度提升1倍,等效天线增益可提升3dB。稀疏阵列和密集阵列相比,使用了80个等效相位中心,而密集阵列只使用了40个等效相位中心,其等效长度提高了1倍。对稀疏阵列进行1次孔径综合后,剩余的等效相位中心还可组成两组近似满阵的阵列。因此,系统信噪比为:
| ${\rm{SN}}{{\rm{R}}_{{\rm{sp}}}}= {\rm{SN}}{{\rm{R}}_{\rm{2}}} + 3 + 3 + 4:78 = 12:71 \rm{(dB)}$ | (3) |
事实上,由于大多数等效相位中心被弃置,对密集阵列孔径综合并不合适。当密集阵列使用码分信号时,对不同的码分信号应直接使用相干积累,此时密集阵通过相干积累获得的系统信噪比为:
| ${\rm{SN}}{{\rm{R}}_{{\rm{de}}}} = {\rm{SN}}{{\rm{R}}_{\rm{2}}} + 13:2 = 15:14 \rm{(dB)}$ | (4) |
上述分析表明,在宽发窄收条件下,使用稀疏阵列获得的信噪比比密集阵列情况低2dB左右,可用于运动目标探测。 2.2.2 实孔径成像模式
对于对地实孔径成像模式,信噪比公式可以表示为:
| \[{\rm{SNR = }}\frac{{{P_{\rm{t}}}A_{\rm{e}}^{\rm{2}}{\sigma _0}{\delta _{\rm{r}}}\tau }}{{{\rm{4\pi }}{R^{\rm{3}}}\lambda L{\rm{k}}{T_{\rm{s}}}{F_{\rm{n}}}{L_{\rm{a}}}{\rm{sin}}\theta }}\] | (5) |
通过以上对组合巴克码稀疏阵列天线雷达的性能分析表明,在宽发窄收条件下,相比于密集阵列天线,稀疏阵列天线雷达在运动目标探测模式下的信噪比降低了约2dB。但从图 3可知,稀疏阵列的阵列长度相为密集阵列长度的2倍,对应的空间分辨率提高了1倍,易于实现对地实孔径成像。 3 稀疏阵列实孔径对地成像
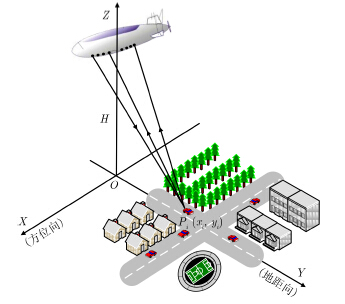
由于运动目标在杂波抑制后在空间域是稀疏的,相关的研究工作已存在较多[5],本文在此不做更深入的研究,着重研究基于变换域稀疏的对地成像。艇载共形稀疏阵列天线雷达系统的成像几何模型如图 4所示。$X$-$Y$(方位向-地距向)平面为成像平面,稀疏阵列天线沿$X$轴方向分布在艇身底部,即共形稀疏阵列天线分布在$X$-$Z$平面,飞艇悬停高度为H。
|
图 4 艇载共形稀疏阵列天线雷达系统成像几何模型 Fig.4 The geometry of airship conformal sparse array antenna radar system |
令第$m$个子阵的空间位置为$r_m=(u_m,0,w_m)$,发射的信号为$p_m(t)$。假设被观测场景中第i个散射点的空间位置为$P_i=(x_i,y_i,z_i)$,则第$m$个子阵发射,第$n$个子阵接收的回波信号可以表达为:
| $s{\rm{(}}t,{r_m},{r_n}{\rm{) = }}\sum\limits_m {\sum\limits_{_n} {{\sigma _i}} } {p_m}{\rm{(}}t - \tau {\rm{(}}{r_m},{r_n},{P_i}{\rm{))}}$ | (6) |
| $\left. \matrix{ \tau {\rm{(}}{r_m},{r_n},{P_i}{\rm{)}} = \left( {R\left( {{r_m},{P_i}} \right) + R\left( {{r_n},{P_i}} \right)} \right)/ \rm{c} \hfill \cr R\left( {{r_m},{P_i}} \right) = \sqrt {{{\left( {{u_m} - {x_i}} \right)}^2} + {{\left( {{y_i}} \right)}^2} + {{\left( {{w_m} - {z_i}} \right)}^2}} \hfill \cr R\left( {{r_n},{P_i}} \right) = \sqrt {{{\left( {{u_n} - {x_i}} \right)}^2} + {{\left( {{y_i}} \right)}^2} + {{\left( {{w_n} - {z_i}} \right)}^2}} \hfill \cr} \right\}$ | (7) |
如上所述,本文所设计的阵列呈曲线分布,且阵列较长,为避免复杂的相位中心补偿和距离徙动校正处理,本文利用基于CS的方法直接对回波信号进行2维联合处理(方位向-地距向)。若数据量过大,可在未来的工作中考虑2维解耦或者分块处理的思路。将待重建的图像区域划分为$N_x×N_y$个网格单元,每个单元代表一个散射点。设第$i$行,第$j$列散射点$P_{ij}=(x_i,y_i,0)$的散射系数为$σ_{ij}$,待重建图像可以表示为:
| $\theta = {\left[ {{\sigma _{11}} \cdot \cdot \cdot {\sigma _{1Ny}}{\sigma _{21}} \cdot \cdot \cdot {\sigma _{2Ny}} \cdot \cdot \cdot {\sigma _{{N_x}1}} \cdot \cdot \cdot {\sigma _{{N_x}{N_y}}}} \right]^\rm{T}}$ | (8) |
将快时间$t$离散化,令$t=[t_1,t_2,···,t_{N_r}]^\rm{T}$,其中$N_r$为距离向采样点数,则第$m$个子阵发射,所有子阵接收的回波信号构成的观测数据可表示为:
| ${y_m} = {\left[ {s{{\left( {t,{r_m},{r_1}} \right)}^{\rm{T}}}s{{\left( {t,{r_m},{r_2}} \right)}^{\rm{T}}} \cdot \cdot \cdot s{{\left( {t,{r_m},{r_M}} \right)}^{\rm{T}}}} \right]^{\rm{T}}}$ | (9) |
| ${\varPhi _m} = \left[ \matrix{ {p_m}{\rm{(}}t - {\tau _1}{\rm{(}}{r_m},{r_1}{\rm{))}} \hfill \cr {p_m}{\rm{(}}t - {\tau _2}{\rm{(}}{r_m},{r_2}{\rm{))}} \hfill \cr \qquad \qquad \vdots \hfill \cr {p_m}{\rm{(}}t - {\tau _M}{\rm{(}}{r_m},{r_M}{\rm{))}} \hfill \cr} \right]$ | (10) |
| $\eqalign{ & p{\rm{(}}t - {\tau _l}{\rm{(}}{r_m},{r_l}{\rm{))}} \cr & \quad {\rm{ = }}\left[ {{p_m}{\rm{(}}t - \tau {\rm{(}}{r_m},{r_l},{P_{11}}{\rm{))}} \cdots \\ \qquad \quad {p_m}{\rm{(}}t - \tau {\rm{(}}{r_m},{r_l},{P_{1Ny}}{\rm{))}} \cdots \\ \qquad \qquad {p_m}{\rm{(}}t - \tau {\rm{(}}{r_m},{r_l},{P_{NxNy}}{\rm{))}} \cdots } \right] \cr} $ | (11) |
综合上式,可得到回波与场景之间的观测方程
| $y_m =\varPhi_mθ$ | (12) |
由于目标在空间的分布通常是连续的,其图像应具有可压缩性,可以被稀疏表示[12, 13, 14]。但SAR图像通常为复数,其分辨单元的尺度通常远大于波长量级,由此形成的散射单元随机初相位使SAR复图像频谱较宽,其复图像难以稀疏表示,这使得CS无法直接求解式(12)。
然而,飞艇悬停驻留的特点,为图像的稀疏表示创造了条件。利用前后两个时刻的脉冲对场景分别进行实孔径成像,可获得两幅地物的图像。两幅图像获得的相位基本相同,对成像的结果进行干涉处理,则可消除散射单元的随机初相位。
如图 5所示,原始SAR复图像的频谱分布在由信号带宽和多普勒带宽决定的较宽的范围内,频谱是不稀疏的。而进行干涉处理后,由于消除了消除散射单元的随机初相位,其频谱主要集中在零频附近,2维频谱带宽已明显变窄。这说明干涉处理可以实现降低信号带宽的目的。
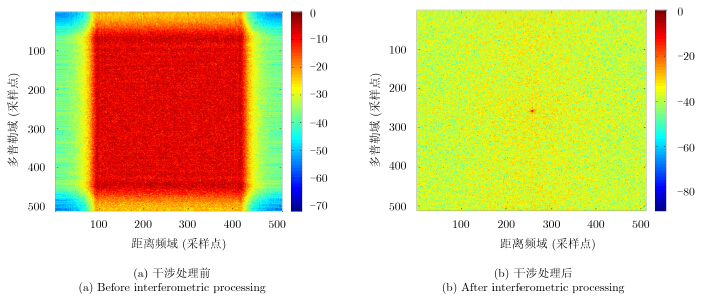
|
图 5 SAR图像频谱 Fig.5 The frequency sprecturm of SAR image |
使用BP算法对时刻2获得的信号进行成像,可获得图像的相位P。那么,待重建的图像可以表示为:
| $\theta = P{\theta \rm{_{new}}}$ | (13) |
| ${\theta \rm{_{new}}} = F\alpha $ | (14) |
| ${y_m} = {Φ _m}PF\alpha $ | (15) |
由于$\alpha$是稀疏的,可以使用CS理论中的稀疏重建算法求解$\alpha$,并逆变换获得待重建的场景$\theta$。由于相关文献已证明干涉后的SAR图像在频域是稀疏的[9, 12],故本文的变换域选为频域,即$F$选为逆傅里叶矩阵。其它变换域,如小波域,也可适用于本方法,关于干涉后图像的稀疏表示问题值得进一步研究[15]。需要说明的是,由于有$M$个接收子阵,可以获得$M$个如式(12)的方程式。根据工作模式的不同,可将这$M$个方程分别求解后对M个解进行相干累加获得最终结果,以提升图像信噪比;或者联合$M$个方程式求解$\theta$,获取高分辨率的图像。 4 仿真试验
4.1 圆锥场景仿真
本节给出了仿真数据的成像结果,以验证本文方法的有效性。本节仿真中,采用基于${\ell ^{{\rm{1/2}}}}$范数的最优化方法[16]求解变换域系数,最终获得图像。有关算法求解的具体步骤较为复杂,在此不再赘述,关于算法的复杂度和运算量,可参考文献[17]。图 6显示了仿真场景。在此选用一个包含椭圆锥的场景而非点目标场景(空间稀疏)来进行仿真试验。仿真的圆锥高为50m,椭圆锥长轴为100m,短轴约40m,位于100m×280m(方位×地距)大小的平面上。圆锥的后向散射系数为1,地面的后向散射系数为0.3。仿真采用单发多收模式,第2.1节所述的共形稀疏阵列中第1个子阵发射线性调频信号,其中$f_m$为第$m$个子阵发射信号的中心频率,$k \rm{_r}$为调频率。
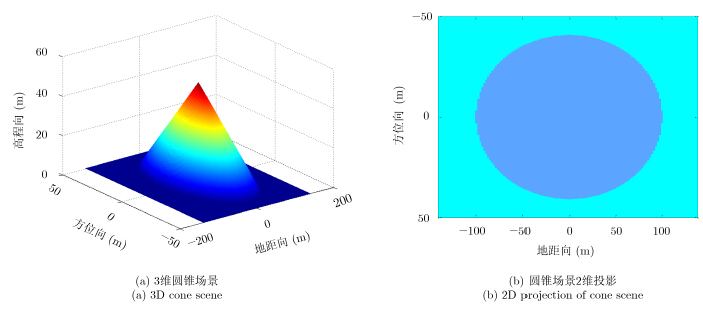
|
图 6 仿真圆锥场景 Fig.6 Simulated cone scene |
| ${p_m}\left( t \right) = \rm{rect}\left[ {{t \over {{T_p}}}} \right] \cdot \exp \left[ {\rm{j2\pi} \left( {{f_m}t + {{{k \rm{_r}}} \over 2}{t^2}} \right)} \right]$ | (16) |
所有21个阵元接收信号,发射信号的带宽设为100MHz。为了减小数据量,脉冲宽度Tp设为1μs,此时观测矩阵的大小约为5000×35000,其余参数详见表 1。
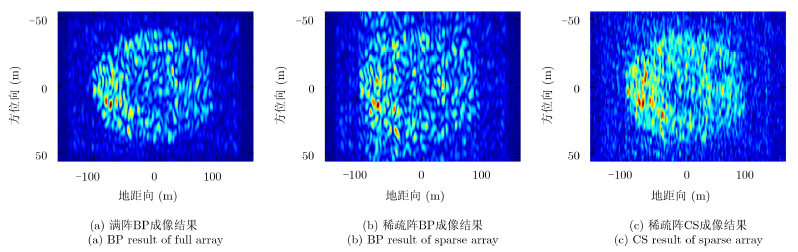
图 7分别显示了单发多收模式下采用满阵(44个子阵)BP成像、稀疏阵列(21个子阵)BP成像和稀疏阵列CS成像的结果。图 8为同样条件下添加噪声后的成像结果,单脉冲信噪比(Signal-to-Noise Ratio,SNR)为10dB。从图中可看出,同样是稀疏阵列,使用CS方法,可以有效地降低旁瓣的影响,而传统的BP方法则不行。虽然仍有一定的副瓣干扰,但使用CS方法在稀疏阵条件下可以获得与满阵接近的效果。
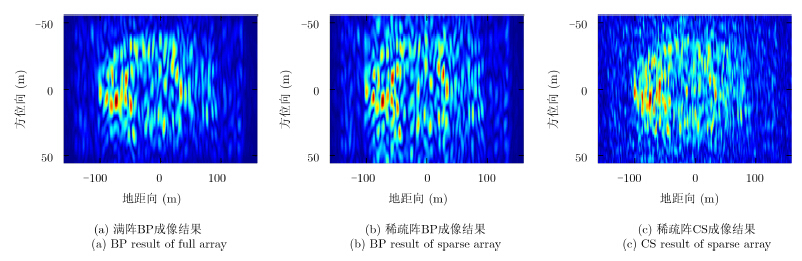
|
图 7 单发多收模式成像结果(无噪声) Fig.7 SIMO mode imaging result(noise free) |
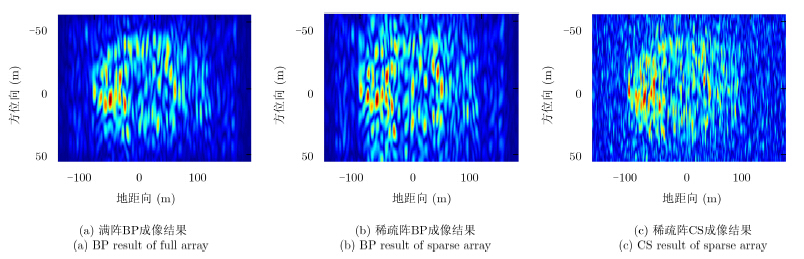
|
图 8 单发多收模式成像结果(SNR = 10 dB) Fig.8 SIMO mode imaging result(SNR = 10 dB) |
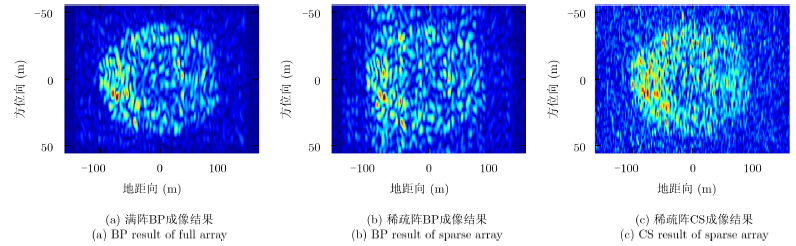
由于单发多收阵列的等效阵长只有满阵的一半,该模式下方位向分辨率较低(约14m),成像结果不易直观反映目标的信息,故本文又给出了多发多收(Multiple Input Multiple Output,MIMO)模式下的成像结果。此时,等效阵长与满阵相同,方位向分辨率为6.8m,成像结果见图 9和图 10。从图中可见,采用本文方法对稀疏阵列成像可达到接近满阵成像的效果。为了更准确地评价本文方法,在此使用均方根误差MSE来比较重建图像的质量。使用真实场景的图像做参考,分别与满阵BP,稀疏阵BP和稀疏阵CS方法的结果进行比较,具体结果见表 2。
|
图 9 多发多收模式成像结果(无噪声) Fig.9 MIMO mode imaging result (noise free) |
|
图 10 多发多收模式成像结果(SNR = 10 dB) Fig.10 MIMO mode imaging result (SNR = 10 dB) |
| 表 2 重建图像评价结果 Tab. 2 Evaluation of the reconstruction results |
从表 2中数据可以看出,本文基于CS的方法,在稀疏阵列条件下,可获得接近传统BP方法满阵成像的效果。由于阵型、变换基等因素的影响,一些成像结果存在高副瓣的影响,但综合来说,基于CS方法远优于稀疏阵列BP的成像效果。除此之外,CS方法易受到噪声的影响,本文仿真中噪声水平较低的情况下,图像质量已受到一定影响。本文方法如何应用到低信噪比条件下,值得进一步研究。 4.2 正交信号成像分析
在4.1节中,本文对单发多收模式下系统成像性能进行了仿真,但成像分辨率较多发多收模式低。为进一步提高成像分辨率,需考虑使用正交信号实现多发多收,本文在此简单地分析了不同正交信号(频分信号,码分信号和OFD Mchirp信号)在对地成像时的性能及特点。
本文使用了频分信号多发多收模式,该信号正交性较好,且对多普勒不敏感。但使用频分信号时,需要轮流发射不同子频信号等效换取(即2.2节分析的情况),无法使用1次脉冲获取等效满阵阵长,不适合强调时间要求的场合。
若采用码分信号,则不需要轮发不同频率的子带信号,使用单脉冲即可获得等效满阵阵长的稀疏阵列,从而实现实孔径成像。本文以Gold码为例分析码分信号的特点。Gold码由m序列优选对生成[18],当寄存器阶数$n$增加时,Gold码序列的数量远多于m序列的数量且Gold码序列具有良好的自相关特性和互相关特性,适合在多发多收系统中使用。Gold码的互相关函数为如下的3值函数:
| ${R_{a,b}} = \left\{ \matrix{ - 1/p \hfill \cr - t/p \hfill \cr \left( {t - 2} \right)/p \hfill \cr} \right.$ | (17) |
OFDM chirp信号是近几年MIMO领域研究的热点[19, 20],该信号具有频谱利用率高,峰均比低等特点,也可在1次脉冲获得等效满阵的效果。但同码分信号一样,互相关特性影响其成像性能。如文献[20]中所示,由于互相关的影响,MIMO的成像性能较单发单收系统略差,其在对地成像中的应用需要更深入的研究。 5 结束语
本文研究了基于变换域稀疏压缩感知的艇载雷达共形稀疏阵列对地成像技术。针对飞艇平台,本文设计了基于组合巴克码的共形稀疏阵列,并分析了其探测性能,证明在运动目标探测模式下,本文稀疏阵列的探测信噪比仅比密集阵列低2dB左右,但等效阵长可提升1倍;在实孔径成像模式下,本文稀疏阵列也满足对地成像要求。针对本文的共形稀疏阵列,提出了基于CS的对地成像信号处理方法。利用前后不同时刻两次脉冲实孔径成像的结果,可去除散射单元的随机初相位,使图像在变换域稀疏,从而可以使用CS方法重建场景,使用本文方法对稀疏阵列信号成像可获得接近满阵成像的效果。
需要说明的是,本文提出的成像方法,可以进一步扩展到多脉冲成像中。每次成像时,均可用已获得图像的信息,去除下一时刻脉冲图像散射单元的随机初相位,依次迭代获得新的图像,提高图像质量。
| [1] | Barbier C, Delauré B, and Lavie A. Strategic research agenda for high-altitude aircraft and airship remote sensing applications[C]. USE-High Altitude Aircrafts and Airships Workshop, Antwerp, Belgium, 2006: 44–49.( 1) 1) |
| [2] | 李道京, 侯颖妮, 滕秀敏, 等. 稀疏阵列天线雷达技术及其应用[M]. 北京: 科学出版社, 2014: 9–40. Li Dao-jing, Hou Ying-ni, Teng Xiu-min, et al.. Sparse Array Antenna Radar Imaging Technologyand Application[M]. Beijing: Science Press, 2014: 9–40.( 2) 2) |
| [3] | Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306.( 1) 1) |
| [4] | Cands E and Romberg J. Sparsity and incoherence in compressive sampling[J]. Inverse Problems, 2007, 23(3): 969–988.( 1) 1) |
| [5] | 滕秀敏, 李道京. 艇载共形稀疏阵列天线雷达成像研究[J]. 电波科学学报, 2012, 27(4): 644–649, 656. Teng Xiu-min and Li Dao-jing. Study on airship conformal sparse array radar imaging[J]. Chinese Journal of Radio Sciences, 2012, 27(4): 644–649, 656.(  4) 4) |
| [6] | Zhu X X and Bamler R. Superresolving SAR tomography for multidimensional imaging of urban areas: compressive sensing-based TomoSAR inversion[J]. Signal Processing Magazine, 2014, 31(4): 51–58.( 2) 2) |
| [7] | 吴一戎, 洪文, 张冰尘, 等. 稀疏微波成像研究进展[J]. 雷达学报, 2014, 3(4): 383–395. Wu Yi-rong, Hong Wen, Zhang Bing-chen, et al.. Current developments of sparse microwave imaging[J]. Journal of Radars, 2014, 3(4): 383–395.(  1) 1) |
| [8] | Zhang L, Xing M, Qiu C-W, et al.. Achieving higher resolution ISAR imaging with limited pulses via compressed sampling[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 567–571.( 1) 1) |
| [9] | 李烈辰, 李道京. 基于压缩感知的连续场景稀疏阵列SAR三维成像[J]. 电子与信息学报, 2014, 36(9): 2166–2172. Li Lie-chen and Li Dao-jing. Sparse array SAR 3D imaging for continuous scene based on compressed sensing[J].Journal of Electronics & Information Technology, 2014, 36(9): 2166–2172.(  3) 3) |
| [10] | 杨波. 一种设计组合巴克码脉冲压缩旁瓣抑制滤波器的新方法[J]. 现代雷达, 2001, 23(5): 41–45. Yang Bo. A new method for designing range-sidelobe suppression filter for combined Barker code[J]. Modern Radar, 2001, 23(5): 41–45.(  1) 1) |
| [11] | Li L and Li D. Airship sparse array antenna radar performance analysis[C]. 2013 IEEE International Geoscience & Remote Sensing Symposium, Melbourne, Australia, 2013: 628–631.( 1) 1) |
| [12] | Li D, Zhang Q, Li L, et al.. Sparsity analysis of SAR signal and three-dimensional imaging of sparse array SAR[C]. 2013 IEEE International Geoscience & Remote Sensing Symposium, Melbourne, Australia, 2013: 891–894.( 2) 2) |
| [13] | 张清娟, 李道京. 干涉SAR图像数据压缩[J]. 中国科学院研究生院学报, 2013, 30(3): 380–386. Zhang Qing-juan and Li Dao-jing. InSAR imaging data compression[J]. Journal of Graduate University of Chinese Academy of Sciences, 2013, 30(3): 380–386.(  1) 1) |
| [14] | Li L, Li D, and Pan Z. InSAR signal sparse sampling and processing based on compressed sensing[C]. 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 2014: 1041–1044.( 1) 1) |
| [15] | Xu G, Xing M-D, Xia X-G, et al.. Sparse regularization of interferometric phase and amplitude for InSAR image formation based on Bayesian representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2123–2136.( 1) 1) |
| [16] | Zeng J, Fang J, and Xu Z. Sparse SAR imaging based on L1/2 regularization[J]. SCIENCE CHINA Information Sciences, 2012, 55(8): 1755–1775.( 1) 1) |
| [17] | Zeng J, Xu Z, Zhang B, et al.. Accelerated L1/2 regularization based SAR imaging via BCR and reduced Newton skills[J]. Signal Processing, 2013, 93(7): 1831–1844.( 1) 1) |
| [18] | 辛肖明, 陈琼. m序列优选对及平衡Gold码序列[J]. 北京理工大学学报, 1990, 10(4): 106–113. Xin Xiao-ming and Chen Qiong. Optimum m-sequence pairs and balanced gold group[J]. Journal of Beijing Institute of Technology, 1990, 10(4): 106–113.(  1) 1) |
| [19] | Kim J H, Younis M, and Moreira A. A novel OFDM chirp waveform scheme for use of multiple transmitters in SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 6(3): 568–572.( 1) 1) |
| [20] | Wang W Q. MIMO SAR OFDM chirp waveform diversity design with random matrix modulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1615–1625.( 2) 2) |


