②中国科学院大学, 北京, 100190
②Graduate University of Chinese Academy of Sciences, Beijing 100190, China
在现代战争环境中,利用无人机等小型飞行平台,对敌方坦克、步兵车和小股作战部队等地面动目标实施全天时、全天候地精确跟踪打击,是一种科学战胜敌军的重要军事手段。为了保证准确有效地追踪目标,低空飞行器必须装备现代化的图像感知设备来探测和识别这些可疑目标,并对关心区域进行高精度实时成像。目前,低空飞行平台装备的目标探测系统主要包括红外/可见光传感器和合成孔径雷达(Synthetic Aperture Radars,SAR)两种[1, 2, 3, 4],但红外/可见光传感器无法穿透云层成像,常规机载SAR可对静止场景和目标实现高分辨成像,采用地面动目标指示技术可实现运动目标的检测和定位[5, 6],但所需积累时间长,成像帧率仅约为0.1 Hz,不能实现对特定运动目标的跟踪,无法满足机动作战、快速响应的军事需求。
针对常规机载SAR存在的成像速率低、慢动目标检测困难等问题,有必要研制一种新型高帧率合成孔径雷达系统,它能够全天时、全天候、高精度地对地面目标区域进行实时成像,并能有效探测和跟踪慢速运动目标,从而提高攻击机和低空无人机的侦察打击能力。若能在现有低空飞行器上装备高性能SAR成像系统,不仅能有效克服红外/可见光传感器易受天气条件和战场环境影响的弱点,也能克服常规SAR系统帧速低、动目标检测跟踪难等缺陷,通过一帧帧清晰影像的渐变显现形成视觉活动图像,使作战指挥人员能够更加直观地感知目标区域的动态信息,有效提升我军的侦察能力和机动作战能力。
2012年5月美国国防部先进研究项目局(Defense Advanced Research Projects Agency,DARPA)发布了一项名为视频合成孔径雷达(Video Synthetic Aperture Radar,ViSAR)的研究项目[7, 8],目标是研发一种工作在太赫兹频段的高分辨率全动态视频合成孔径雷达,能够穿透云、烟尘等障碍物对地面目标进行成像探测和跟踪,并且可借助云雾天气保护自身不受敌方攻击。项目设定ViSAR系统分辨率为0.2 m,图像帧速率大于5 Hz,并拟采用“一发四收”的多天线技术实现运动目标的有效探测和精确重定位。
随着载波频率的提高,成像结果对平台运动误差越来越敏感,对运动补偿的精度要求也越来越高,因此给运动补偿带来了很大的困难,限制了ViSAR的发展。对高分辨率机载SAR来说,运动补偿方法主要分为基于运动传感器数据补偿和基于回波数据补偿两种方法[9, 10],补偿后微波段SAR图像成像质量大幅提高。然而,对工作在太赫兹频段的ViSAR系统而言,平台的微小高频振动如载机内部振动可导致ViSAR系统散焦严重[11]。根据国家军用标准关于环境适应性的试验规定(GJB150.16-86)[12],机载平台振动误差环境主要可分为螺旋桨飞机、喷气式飞机和直升机3种,其中螺旋桨飞机和喷气式飞机振动量级在毫米级,已有的运动传感器系统可能无法测量出其低振幅高频振动,且图像散焦严重时,无法基于回波数据利用自聚焦技术进行补偿,因此直接照搬微波段SAR运动补偿技术行不通。目前仍未见有关ViSAR平台微小振动误差定量分析及其运动补偿方法的公开报道。
因此本文研究了振动误差对ViSAR成像的影响,并提出一种有效的运动补偿方案。主要内容包括从大气衰减条件及成像帧速要求等确定系统参数;建立正弦振动误差作为理论误差模型,分析振动误差对回波信号相位影响,定量分析ViSAR补偿后可允许剩余运动误差阈值与振动频率的关系,根据理论分析结果,并结合微波段SAR与激光SAR补偿方法研究,提出一种有效的运动误差补偿方案,即结合光学隔振技术、基于低精度运动测量数据粗补偿和基于回波数据自聚焦技术精补偿的3级运动补偿法。并通过在点目标仿真成像结果中加入喷气式飞机随机振动误差,进行仿真验证,补偿结果验证了该方案的有效性。
2 ViSAR系统参数设计根据美国DAPRA论证,在SAR图像中,能够精确区分地面移动部队、车辆,甚至单人移动目标所需的距离向及方位向分辨率$\delta_\rm{a}$均需达到0.2 m。ViSAR主要探测跟踪对象是小型机动目标,其速度范围为1~10 m/s,横向加速度范围是0.98~9.8 m/s2。成像系统在满足分辨率为0.2 m的条件下,采用视频图像技术要实现对最小速度为1 m/s的目标进行检测跟踪,成像帧率应不低于5 Hz。假设目标与雷达斜距为R0,平台飞行速度为v以及方位向分辨率为$\delta_\rm{a}$,系统工作频率fc与成像帧率Fr的关系为${\mathit{f}_{\rm{c}}} = \frac{{{\rm{c}}{R_0}}}{{2v{\delta_\rm{a}}}}{\mathit{f}_{\rm{r}}}$。为实现5 Hz的成像帧率,当雷达与目标之间的斜距为5 km,载机飞行速度为100 m/s,方位向分辨率为0.2 m时,在帧率Fr=5 Hz的要求下,系统工作频率至少应为fc= 187.5 GHz。因此,要完成ViSAR系统对地面移动目标的跟踪监测,雷达系统工作频率需在187.5 GHz以上。
而水蒸气和氧气对太赫兹波衰减影响比较严重,极化分子与入射波作用会产生强烈吸收,同时空中的水分凝结物(如雨、雾、雷、霜、云等)会引起附加的衰减。大气中水分对毫米波与太赫兹频段电磁波的衰减,最严重的可达到100 dB/km以上[13, 14]。在高于187.5 GHz频段,国际公认的大气衰减窗口主要为220 GHz,340 GHz,420 GHz,580 GHz,670 GHz等。图 1为夏季中纬地区标准天气状况下的地表大气衰减曲线,此时大气基本参数为:温度295 K,大气压1013 hpa,湿度74%。
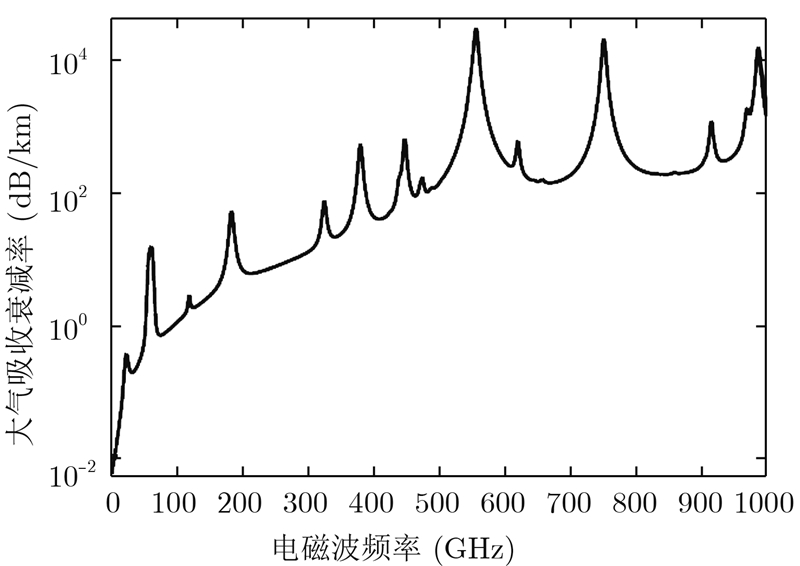 | 图 1 夏季中纬地区标准天气状况下的地表大气衰减曲线Fig. 1 Surface atmospheric attenuation curve in summer mid-latitude regions under standard weather condition |
从图 1可以看出,可选择大气衰减相对较小的220 GHz或340 GHz窗口作为ViSAR系统的工作频段。通过进一步定量地比较这两个频率窗口的大气吸收特性,可知 340 GHz处的大气衰减要比220 GHz处严重得多,在湿度80%的大雾天气下,二者大气衰减分别达到15 dB/km和10 dB/km。因此,从大气衰减角度来说,选择220 GHz作为ViSAR系统的工作频率是合理的。
当ViSAR系统工作在正侧视条带模式下时,ViSAR系统参数如表 1所示。
| 表 1 ViSAR系统仿真参数Tab. 1 Simulation parameters of ViSAR |
对ViSAR系统而言,合成孔径时间很短,方位聚焦深度 $\Delta {R_m} = \Delta R(t = T/2) = \frac{{V^{\hspace{1pt} 2}{T ^{\hspace{1pt} 2}}}}{{8R}}$,代入表 1参数计算可得$\Delta {R_m}$约为0.006 m,小于距离向分辨单元的1/8,因此可忽略距离徙动影响[15],无需进行距离徙动校正。因此系统成像算法将直接采用距离多普勒(Range Doppler,RD)算法。这将大大简化成像算法,利于高帧率实时动目标监测。
然而,工作在太赫兹频段的ViSAR相比微波SAR而言,波长较短,使其具有短时间获得高帧速高分辨率图像的可能性,但与之相对应,载机平台的微小振动都会引起信号相位的显著变化,而这种微小振动可能无法通过现有的运动传感器测得,但仍会导致成像结果失焦,这给ViSAR成像处理带来许多困难。
3 正弦运动误差理论推导与定量分析本文通过建立正弦运动误差模型,推导出振动误差对3个方向上产生的回波相位误差及对成像质量的影响[16],并定量分析振动误差幅度阈值与振动频率的关系,确定运动补偿精度。若平台微小振动误差幅度小于理论误差阈值,可认为对成像并无影响。
以条带模式正侧视ViSAR为例进行分析,其简单几何运动模型如图 2所示,其中理想运动路线为沿平行于X轴方向匀速移动,而曲线代表实际运动路线。理想单点目标回波信号为
| $ \begin{aligned} S_\rm{out}(t,t_m) = & a_{\rm{r}} \left( {t - \frac{{2R(t_m)}}{\rm{c}}} \right) \\ & \cdot \exp \left[{{\rm{j {π} }} K_{\rm{r}}{{\left( {t - \frac{{2R(t_m)}}{\rm{c}}} \right)}^2}} \right]\\ & \cdot \exp \left[{ - {\rm{j}}\frac{{4 {π} }}{\lambda }R(t_m)} \right] \end{aligned}$ | (1) |
式中t为距离向快时间,tm 为方位向慢时间,第1项为包络延时项,ar为其包络幅度,第2项为距离向线性调频信号,$\mathit{K}_{\rm{r}}$为线性调频信号调频率,R(tm)为目标斜距,c为光速,第3项为多普勒频移产生的方位向相位,l为载波波长。
 | 图 2 ViSAR 运动几何模型图Fig. 2 ViSAR motion geometry model |
实际航迹可表示为[X(tm),Y(tm),Z(tm)],而理想航迹可表示为[Vtm,0,H],H为雷达飞行高度,两种航迹的坐标差即为位置的3个误差分量,可表示为DX = X(tm)-Vtm,DY = Y(tm),DZ = Z(tm)-H。为分析方便,假设其中一点目标位置坐标为Pn(0,Yn,0),此时实际雷达天线相位中心(Antenna Phase Center,APC)到Pn点的距离为
| \begin{aligned} R({t_m}) = & \sqrt {X{{({t_m})}^2} + {{(Y \hspace{1pt} ({t_m}) - {Y_n})}^2} + Z{{({t_m})}^2}} \\ = & \Big( {R_0^2} + {{(V \hspace{1pt} {t_m} + \Delta X)}^2} + \Delta {{Y \hspace{3pt}} ^2} + \Delta {Z^2} \\ & - 2{Y_n}\Delta Y + 2H\Delta Z \Big)^{1/2} \end{aligned} | (2) |
其中最近斜距${R_0} = \sqrt {{Y_n}^2 + {H^2}} $,由于式(2)中其余项远小于R0,对式(2)利用菲涅尔近似可得
| $R(t_m) \approx R_0 + \frac{{{{(V \hspace{1pt} t_m + \Delta X)}^2}}}{{2R_0}} - \Delta Y\sin \theta + \Delta Z\cos \theta $ | (3) |
式中设$H = {R_0}\cos \beta ,Y_n = {R_0}\sin \beta$ ,不同平移运动误差DX,DY,DZ会产生不同方位向相位误差,进而影响ViSAR成像质量。
以Z方向运动误差分析为例,设$\Delta Z =$ $\Delta Z = A\sin ({\omega _m}{t_m} + \mathit{\Phi} _0)$,其中${\omega _m}{\rm{ = }}2 {π} m/T \hspace{2pt}$ ,其中m 表示在合成孔径时间内起伏的周数,T为合成孔径时间。当 0<m<0.5时称为低频振动,0.5<m<2时称为中频振动,m>2时称为高频振动。将正弦运动误差模型公式代入式(1)推导可得Z方向方位向相位误差为
| $\Delta \alpha (t) = - \frac{{4 {π} }}{\lambda }{A\sin ({\omega _m}{t_m} + {\mathit{\Phi} _0})\cos \theta }$ | (4) |
其中,低频振动主要造成2次相位畸变,分辨率下降。高频振动主要造成旁瓣电平升高,积分旁瓣比也随之增大。中频振动则比较复杂,除考虑主瓣展宽外,主瓣偏移及旁瓣增大也必须考虑。
(1) 正弦低频振动
由于低频振动主要造成2次相位误差,可将式(4)展成泰勒级数为
| $\begin{aligned} \Delta \alpha (t) = & - \frac{{4 {π} }}{\lambda }{A\sin ({\omega _m}{t_m} + {\mathit{\Phi} _0})\cos \theta }\\ = & - \frac{{4 {π} }}{\lambda } A\cos \beta \big[{\sin{\mathit{\Phi} _0}{\rm{ + }}{\omega _m}{\rm{cos}}{\mathit{\Phi} _0}t } \\ & - {\omega _m^2}{\rm{sin}}{\mathit{\Phi} _0}{t^2} + \cdots \big] \end{aligned}$ | (5) |
其2次相位误差项在$\mathit{\Phi} _0{\rm{ = }}{ {π} }/{2},t = {T}/{2} \hspace{2pt} $时达到最大,T为合成孔径时间,设2次相位误差的最大允许值为${({\mathit{\Phi} _{2m}})_m}$,则振动幅度限制为
| $\left| A \right| \le \frac{\lambda }{{ {π} \cos \theta {\omega _m^2}{T \hspace{2pt}}^2}}{({\mathit{\Phi} _{2m}})_m}$ | (6) |
(2) 正弦中频振动
中频振动影响比较复杂,既需考虑1次相位误差,又要考虑2次相位误差。此时将式(4)展成勒让德多项式为
| $\Delta \alpha (t){\rm{ = }}\sum\limits_{n = 0}^\infty {{a_n}{p_n}(t)}$ | (7) |
利用勒让德多项式正交性,经过化简可得
| $\left. {\begin{aligned} {a_0} & = \frac{{4 {π} A\cos \theta \sqrt {T\,\,\,} }}{\lambda }\sin {\mathit{\Phi} _0}{F_0}(m {π} )\\ {a_1} & = \frac{{4 {π} A\cos \theta \sqrt {3T\,\,\,} }}{\lambda }\cos {\mathit{\Phi} _0}{F_1}(m {π} )\\ {a_2} & = \frac{{4 {π} A\cos \theta \sqrt {5T\,\,\,} }}{\lambda }\sin {\mathit{\Phi} _0}{F_2}(m {π} )\\ {a_3} & = \frac{{4 {π} A\cos \theta \sqrt {7T\,\,\,} }}{\lambda }\cos {\mathit{\Phi} _0}{F_3}(m {π} )\\ & \hspace{55pt} \vdots \end{aligned} } \right\}$ | (8) |
且式中
| $\left. \begin{array}{l} {F_0}(m {π} ) = \frac{{\sin m {π} }}{{m {π} }}\\ {F_1}(m {π} ) = - \frac{{\cos m {π} }}{{m {π} }} + \frac{{\sin m {π} }}{{{{(m {π} )}^2}}}\\ {F_2}(m {π} ) = \frac{{\sin m {π} }}{{m {π} }} + \frac{{3\cos m {π} }}{{{{(m {π} )}^2}}} - \frac{{3\sin m {π} }}{{{{(m {π} )}^3}}}\\ \begin{aligned} {F_3}(m {π} ) = & - \frac{{\cos m {π} }}{{m {π} }} + \frac{{6\sin m {π} }}{{{{(m {π} )}^2}}} + \frac{{3\cos m {π} }}{{{{(m {π} )}^3}}} \\ & - \frac{{3\sin m {π} }}{{{{(m {π} )}^4}}} \end{aligned}\\ \\ \quad \quad \quad \quad \quad \quad \vdots \end{array} \right\}$ | (9) |
若从1次相位误差出发来考虑对误差振动幅度的要求,假设偏移值的最大允许值为Dxm,则对幅度限制为
| $\left| A \right| \le \frac{{\lambda \Delta {x_m}}}{{24\cos \theta {π} {F_1}(m {π} )}}$ | (10) |
若设最大允许2次相位误差为${({\mathit{\Phi} _{2m}})_m}$,误差幅度限制为
| $\left| A \right| \le \frac{{\lambda {{({\mathit{\Phi} _{2m}})}_m}}}{{30 {π} \cos \theta {F_2}(m {π} )}}$ | (11) |
(3) 正弦高频振动
高频振动主要造成旁瓣电平增大,按照成对回波理论[16],其ISLR可表示为
| $\rm{ISLR} = \frac{1}{2}{\Bigg( {\frac{{4 {π} }}{\lambda }A\cos \theta }\Bigg )^2} = \frac{{8{ {π} ^2}\cos {\theta ^2}{\mathit{A}^2}}}{{{\lambda ^2}}}$ | (12) |
若给出(ISLR)m的允许值,振动幅度限制为
| $\left| A \right| \le \frac{{\sqrt 2 \lambda }}{{4 {π} \cos \theta }}\sqrt {\left| ( \right.\left. {\rm{ISLR}{)_\mathit{m}}} \right|} $ | (13) |
同理可进行Y轴方向上有关正弦误差的推导。如表 2所示为最终正弦误差Y方向和Z方向理论推导结果。
X方向相位误差为$\Delta \alpha (t) = - \frac{{4 {π} }}{\lambda } \frac{{V \hspace{1pt} {t_m}}}{{{R_0}}}A$ $\cdot \sin ({\omega _m}{t_m} + {\mathit{\Phi} _0})$,可通过仿真手段进行分析。
由以上分析可知,经运动补偿后满足成像质量指标要求时,若剩余相位误差在可容忍范围内,即剩余运动误差小于表 2所示的误差阈值,则认为满足运动补偿精度要求。根据成像质量参数要求,利用仿真手段分析平台振动频率与对应误差幅度阈值的关系。为与微波段SAR进行比较,本文选取载频为22 GH,带宽为1 GHz,天线口径为0.2 m的毫米波SAR系统为对照组,其雷达飞行高度,雷达飞行速度均与ViSAR系统一致,ViSAR系统合成孔径时间约为0.078 s,该对照系统合成孔径时间约为0.78 s。以主瓣展宽不超过4%,ISLR不超过-18 dB,PSLR不超过-20 dB为成像质量参数要求进行仿真。最终得到3个方向上正弦误差振动频率与误差幅度阈值之间的关系如图 3所示。
| 表 2 ViSAR成像对振动误差的要求Tab. 2 Requirements for motion errors of ViSAR imaging |
 | 图 3 不同频段SAR正弦运动误差振动频率与振动误差阈值的关系Fig. 3 Relationship between sinusoidal motion error frequency and threshold in different bands of SAR |
如图 3(a)所示,雷达载频为220 GHz时,X轴方向上振动频率较低时,1次相位误差对成像影响最大,若限定1次相位误差偏离不超过1个方位向分
辨单元,振动频率小于12 Hz时X轴正弦误差幅度阈值为0.3 m左右,此时载机微小振动误差幅度远小于0.3 m,可认为对ViSAR成像结果影响不大。如图 3(b)和图 3(c)所示,由表 3可知,在载频为220 GHz时,当振动频率小于18 Hz时,ViSAR可容忍的误差幅度阈值与合成孔径时间成反比,此时ViSAR系统比同等方位向分辨率微波段SAR补偿难度更小,若振动频率超过18 Hz时,此时可容忍误差幅度阈值仅与波长成正比,其误差阈值在微米级,运动补偿精度要求很高。若载机振动误差幅度超过阈值,可导致ViSAR图像散焦。由此得出结论,较同等分辨率微波段SAR而言,在X轴方向上平台微小振动对ViSAR成像结果影响很小,而Y轴方向和Z轴方向上振动频率较低时更易补偿,振动频率较高时误差补偿难度加大,因此高频振动误差补偿技术是实现ViSAR系统运动补偿的难点。
| 表 3 国内外GPS/INS定位精度调研Tab. 3 Research of domestic and overseas positioning accuracy of GPS/INS |
根据以上分析可知与高分辨率微波段SAR相比,除高频振动补偿难度较大外,其余补偿精度要求均与微波段SAR相当甚至要求更低,但微小的高频振动将导致成像结果完全失焦,因此高频振动补偿是ViSAR运动补偿的重中之重。此外考虑到误差空变性问题,由于ViSAR测绘带较窄,可借鉴微波SAR解决距离向空变性方法,采用距离向划分子带或两步运动补偿技术和成像算法结合可有效补偿距离向运动误差空变问题[17],而由于ViSAR方位向波束宽度$\Delta \theta$仅为0.39°,如果载机在视线方向产生$\Delta R$的误差,在波束边缘处所引起的相位误差是 $\Delta \alpha (t) = \frac{{4 {π} \Delta R}}{\lambda }\cos \left( {\frac{{\Delta \theta }}{2}} \right)$,而在波束中心则引起相位误差为$\Delta \alpha (t) = \frac{{4 {π} \Delta R}}{\lambda }$, 以$\Delta R$值为0.2 m为例,由计算可得二者相位误差值仅相差0.01 rad,因此可忽略误差方位向空变性[18]。以微波段高分辨率SAR和激光SAR补偿方法为参考[19, 20, 21],本文提出了一种ViSAR运动补偿方案,即结合运动传感器测量数据补偿技术、光学隔振平台隔振技术和回波数据自聚焦补偿于一体的3级运动补偿法。通过光学隔振平台隔振技术,初步抑制平台微小振动(第1级);再通过基于GPS/INS数据的粗补偿(第2级),消除回波包络误差和部分相位误差;同时在成像处理中采用条带相位梯度自聚焦( Strip Map Phase Gradient Autofocus,SPGA)方法来进一步抑制振动影响的精补偿[22](第3级),尽可能消除残余相位误差,最终可达到ViSAR系统所要求的补偿精度。
图 4为ViSAR运动补偿流程图。其中基于运动传感器的机载SAR的运动补偿,是指利用载机多种运动传感器来测量载机平台的各种运动状态的数据,从而计算出运动平台的运动误差并且将运动误差造成的影响从雷达数据中消除。由于GPS/INS具有数据率低、长期稳定性好的特点,而天线相位中心处的低成本传感器则有数据率高、精度漂移严重的特点,数据融合后可以对天线相位中心处的运动状态进行高速率的精确测量,并具有长期的稳定性。但通常情况下由于惯导精度及数据率的限制,通过惯导得到的位移仍不够精确,因此只能作为粗补偿。如表 3所示为国内外GPS/INS系统定位精度调研,由表 3可知目前无法通过GPS/INS系统测得毫米级振动误差。
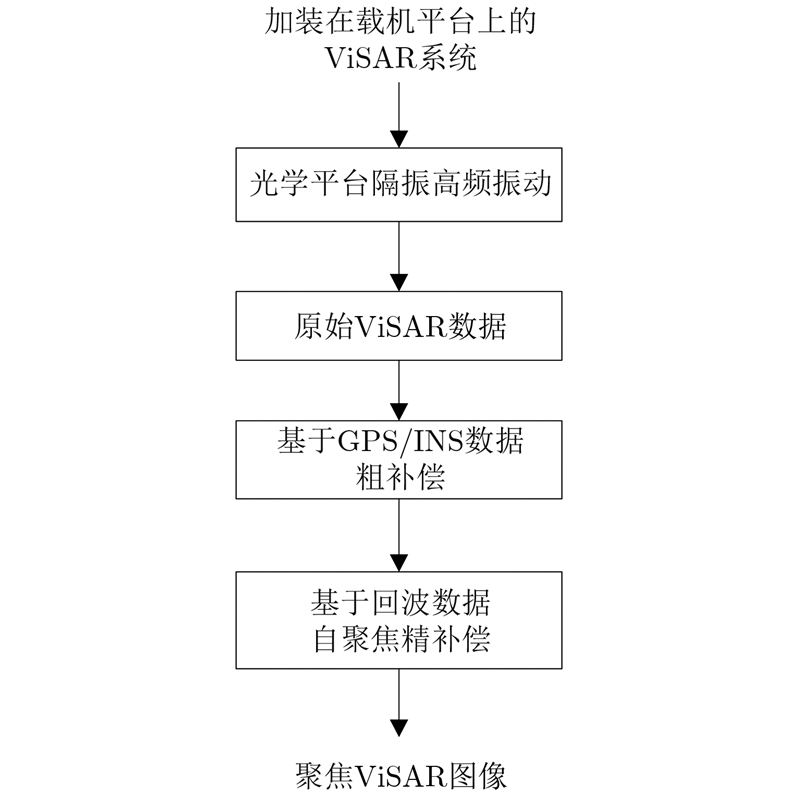 | 图 4 ViSAR运动补偿流程图Fig. 4 Flow diagram of ViSAR motion compensation |
针对高频微小振动,可利用隔振技术,即在振动源和待隔振系统之间的振动传输通道上加装弹性元件,用以减少振动从振动源传输到待隔振系统的能量。隔振大致分为被动隔振、主动隔振和主/被动混合隔振两类。被动隔振是在振动传播途径中加入被动元件,如弹簧,橡胶,空气弹簧等,以减小传递到接收结构的振动强度;主动隔振是在被动隔振的基础上,并联能产生满足一定要求的作动器,或者用作动器代替被动隔振装置的部分或全部元件,通过适当控制作动器的运动,达到减振的目的,适用于超低频隔振。针对ViSAR运动补偿需求,应选择被动隔振技术。
美国Minus K公司研制的BM-10光学隔振平台,采用被动隔振技术,载荷范围为14~25 kg,隔振效果通常比高性能空气系统高出10~100倍,在纳米技术、半导体、材料研究、光学实验等领域有重要应用。该平台在振动频率为2 Hz时可对振动强度达到93%的隔振效率,5 Hz时隔振效率为99%,10 Hz以上时可达到99.9 %的隔振效率,如图 5所示为BM-10平台隔振效果图。
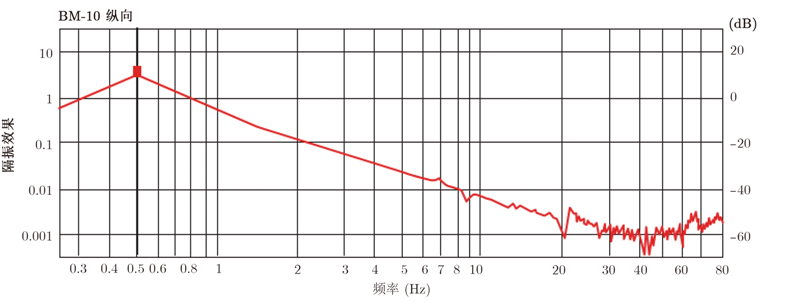 | 图 5 BM-10隔振效果图(纵向)Fig. 5 BM-10 isolation effect drawing (vertical) |
超过10 Hz以上的高频微小振动可通过光学隔振技术进行隔振,有效降低平台振动对ViSAR成像的影响,实现图像一定程度上的聚焦。
为实现ViSAR所需的高补偿精度,基于回波数据的自聚焦算法起着至关重要的作用,它有效地弥补了运动补偿之后的残余误差以及其它各种因素造成的相位误差,相位误差估计的精度依赖于具体的成像场景及采用的自聚焦方法,现有的自聚焦方法包括子孔径相关法(MD)、多子孔径相关法(MAM)、相位差法(PD)和相位梯度自聚焦算法(PGA)等。这些算法都是从相位误差函数出发,目的是得到对相位误差的准确估计,其中MD算法把整个孔径分割成两个子孔径,根据子图像之间的互相关结果估计相位误差,但只能估计2次相位误差,往往不能适应高分辨成像的要求。改进的多子孔径相关算法(MAM)原理上能估计高阶相位误差,但由于子孔径过短使估计结果偏差更大,而ViSAR由于帧速的需求,子孔径仅为几米,因此无法采用这种方法。而PGA算法利用了相位误差的冗余性,通过对相位误差的导数进行估计来完成对相位误差的估计和补偿,从复图像域出发,将散焦的图像聚焦,圆周移位和对图像域数据加窗,最终完成相位梯度估计并实现补偿。针对条带模式ViSAR系统,最终可采用条带相位梯度自聚焦算法(SPGA)进行精补偿。
5 ViSAR成像结果仿真研究为验证该运动补偿方案的有效性,通过在ViSAR系统点目标仿真数据中加入实际飞机振动误差,考虑其对成像结果的影响。振动环境误差主要可分为螺旋桨飞机、喷气式飞机和直升机3种,分别截取各类实测载机高频振动(大于10 Hz)误差轨迹如图 6所示。
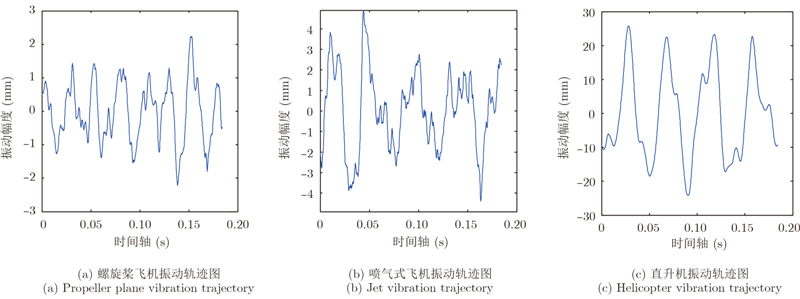 | 图 6 载机随机振动误差轨迹Fig. 6 Random vibration trajectories of different aircrafts |
由图 6可知螺旋桨飞机振动幅度最小,直升机振动幅度已达到分米级,因此最好选择螺旋桨飞机或喷气式飞机作为ViSAR载机平台。以斜距方向上加入喷气式飞机振动误差为例,其微小振动误差将导致ViSAR系统成像结果完全失焦,如图 8所示。图 7为未加误差前的ViSAR成像结果图。
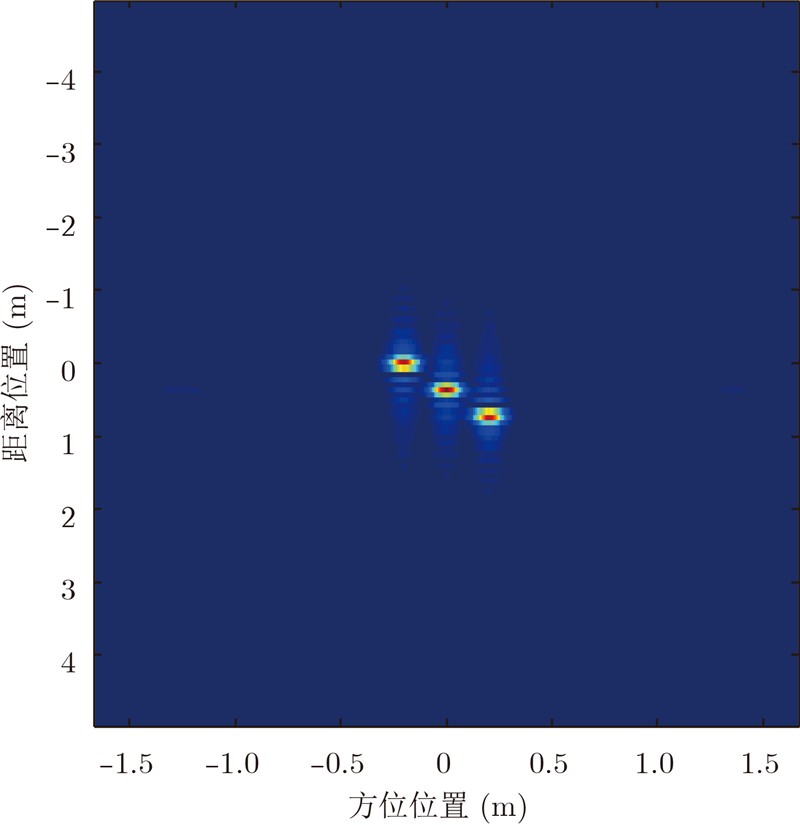 | 图 7 未加振动误差前ViSAR成像结果图Fig. 7 ViSAR imaging result without vibration error |
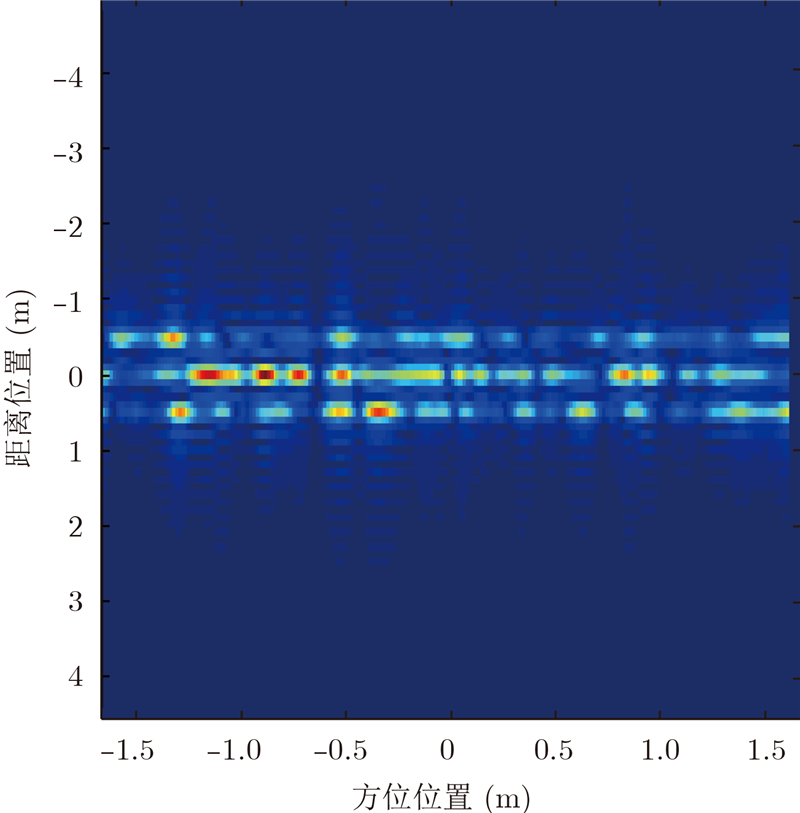 | 图 8 加振动误差后ViSAR成像结果图Fig. 8 ViSAR imaging result with vibration error |
通过逐步仿真可知,当光学隔振平台对振动强度的隔振效率达到99%后即可实现聚焦,隔振后成像结果如图 9所示,此时存在轻微散焦,积分旁瓣比较高,需要进一步精细补偿来提高图像对比度。利用SPGA算法迭代6次后,其特显点的成像参数如表 4所示,结果表明经过该运动补偿方案补偿后成像结果已符合ViSAR成像要求,成像结果如图 10所示。
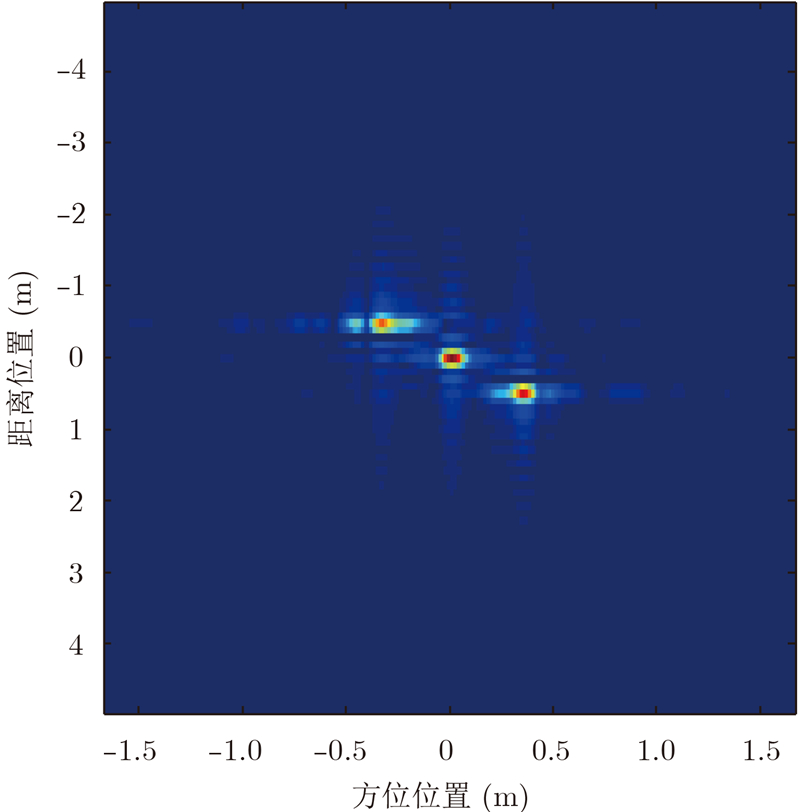 | 图 9 隔振99%后ViSAR成像结果图Fig. 9 ViSAR imaging result by 99% vibration isolation |
| 表 4 补偿后ViSAR成像结果参数Tab. 4 Imaging result parameters of ViSAR after compensation |
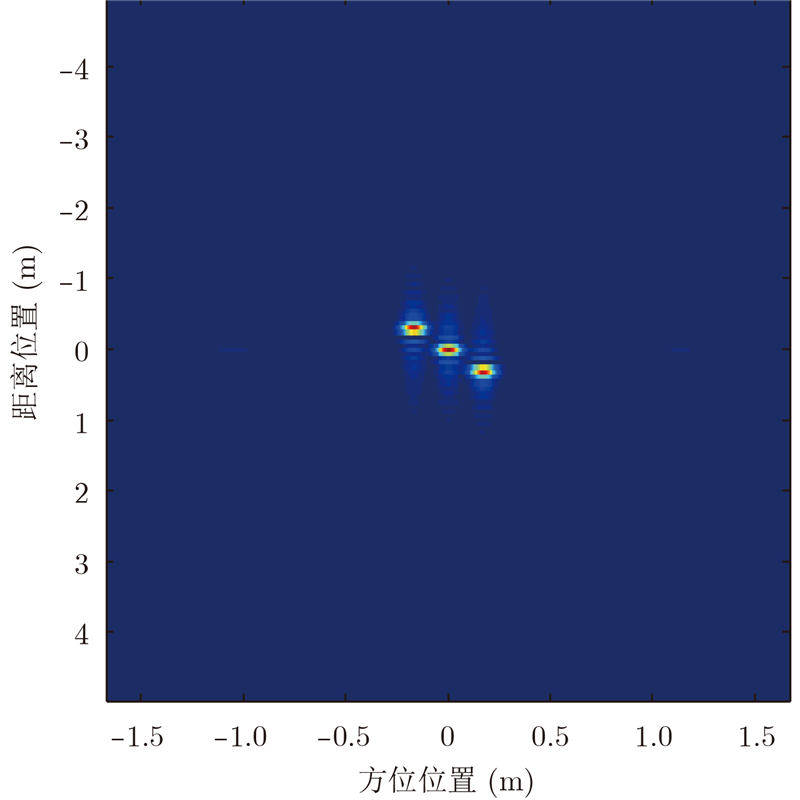 | 图 10 隔振加SPGA补偿后成像结果图Fig. 10 ViSAR imaging result by vibration isolation and SPGA |
本文根据ViSAR系统参数及成像指标定量分析了ViSAR可容忍的剩余振动误差阈值与振动频率的关系。分析表明相比同等分辨率微波段SAR,平台在载机飞行方向的振动和在Y方向和Z方向的低频振动对成像结果影响较小,而在Y方向和Z方向的高频振动对成像结果影响较大,要求补偿精度较高。根据误差理论定量分析,提出结合光学隔振技术、基于运动测量数据粗补偿和基于回波数据自聚焦技术的3级ViSAR运动补偿方案,并通过在仿真中加入实际载机平台振动误差后进行补偿方案验证,结果表明了该补偿方案的有效性,本文为进一步ViSAR系统的设计和数据处理提供了理论基础和实施方案研究。
| [1] | 杨建宇. 雷达技术发展规律和宏观趋势分析[J]. 雷达学报, 2012, 1(1): 19-27. Yang Jian-yu. Development laws and macro trends analysis of radar technology[J]. Journal of Radars, 2012, 1(1): 19-27.(  1) 1) |
| [2] | Cristallini D, Pastina D, Colone F, et al.. Efficient detection and imaging of moving targets in SAR images based on chirp scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(4): 2403-2416.( 1) 1) |
| [3] | Chen Z, Deng T, Gao L, et al.. A novel spatial-temporal detection method of dim infrared moving small target[J]. Infrared Physics & Technology, 2014, 66: 84-96.( 1) 1) |
| [4] | Dong Xia-bin, Huang Xin-sheng, and Zheng Yong-bin. A novel infrared small moving target detection method based on tracking interest points under complicated background[J]. Infrared Physics & Technology, 2014, 65: 36-42.( 1) 1) |
| [5] | Sjogren T K, Vu V, Pettersson M I, et al.. Suppression of clutter in multichannel SAR GMTI[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4005-4013.( 1) 1) |
| [6] | Brenner A R and Ender J H G. Demonstration of advanced reconnaissance techniques with the airborne SAR/GMTI sensor PAMIR[J]. IEE Proceedings-Radar, Sonar and Navigation, 2006, 153(2): 152-162.( 1) 1) |
| [7] | Liu Zhi-wei, Su Ke, Gary E, et al.. Video-rate terahertz interferometric and synthetic aperture imaging[J]. Applied Optics, 2009, 48(19): 3788-3794.( 1) 1) |
| [8] | Linnehan R, Miller J, Bishop E, et al.. An autofocus technique for video-SAR[J]. SPIE, 2013, 8746: 874608-1-874608-10.( 1) 1) |
| [9] | Xing Meng-dao, Jiang Xiu-wei, Wu Ren-biao, et al.. Motion compensation for UAV SAR based on raw radar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(8): 2870-2883.( 1) 1) |
| [10] | Zhu Dai-yin, Jiang Rui, Mao Xin-hua, et al.. Multi-subaperture PGA for SAR auto-focusing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 468-488.( 1) 1) |
| [11] | 沈斌. THz频段SAR成像及微多普勒目标检测与分离技术研究[D]. [硕士论文], 电子科技大学, 2008: 27-35. Shen Bin. SAR imaging and micro-Doppler target detection and separation technology research[D]. [Master dissertation], University of Electronic Science and Technology, 2008: 27-35.(  1) 1) |
| [12] | 中国人民解放军总装备部. GJB 150.16-186国家军用标准-环境[S]. 国防科工委军标出版发行部, 1992. PLA General Armament Department. GJB150.16-186 national military standards environment[S]. National Defense Military Standard Publishing Department, 1992.(  1) 1) |
| [13] | Yang Y, Shutler A, and Grischkowsky D. Measurement of the transmission of the atmosphere from 0.2 to 2 THz[J]. Optics Express, 2011, 19(9): 8830-8838.( 1) 1) |
| [14] | Krupnov A, Golubiatnikov G, Markov V, et al.. Pressure broadening of the rotational line of oxygen at 425 GHz[J]. Journal of Molecular Spectroscopy, 2002, 215(2): 309-311.( 1) 1) |
| [15] | 林华. 无人机载太赫兹合成孔径雷达成像分析与仿真[J]. 信息与电子工程, 2010, 8(4): 373-377. Lin Hua. Analysis and simulation of UAV terahertz wave synthetic aperture radar imaging[J]. Information and Electronic Engineering, 2010, 8(4): 373-377.(  1) 1) |
| [16] | 张澄波. 综合孔径雷达—原理、系统分析与应用[M]. 北京: 科学出版社, 1989: 48-51, 209-323. Zhang Cheng-bo. Synthetic Aperture Radar—Principle, System Analysis and Applications[M]. Beijing: Sciences Publisher, 1989: 48-51, 209-323.(  2) 2) |
| [17] | Fornaro G. Trajectory deviations in airborne SAR: analysis and compensation[J]. IEEE Transations on Aerospace and Electronic Systems, 1999, 35(3): 997-1009.( 1) 1) |
| [18] | 谭鸽伟, 邓云凯. 机载SAR的运动误差的二维空变性及其补偿[J]. 电子与信息学报, 2009, 31(2): 366-369. Tan Ge-wei and Deng Yun-kai. The two-dimensional spatial-variant properties of airborne SAR motion error and its compensation[J]. Journal of Electronics & Information Technology, 2009, 31(2): 366-369.(  1) 1) |
| [19] | 马萌, 李道京, 杜剑波. 振动条件下机载合成孔径激光雷达成像处理[J]. 雷达学报, 2014, 3(5): 591-602. Ma Meng, Li Dao-jing, and Du Jian-bo. Imaging of airborne synthetic aperture ladar under platform vibration condition[J]. Journal of Radars, 2014, 3(5): 591-602.(  1) 1) |
| [20] | 李增局, 吴谨, 刘国国. 振动影响机载合成孔径激光雷达成像初步研究[J]. 光学学报, 2010, 30(4): 995-1001. Li Zeng-ju, Wu Jin, and Liu Guo-guo. Preliminary investigation on airborne SAL imaging with platform vibration[J]. Acta Optica Sinica, 2010, 30(4): 995-1001.(  1) 1) |
| [21] | 张双喜, 孙光才, 周峰, 等. 一种基于子孔径自聚焦的高频运动误差估计和补偿方法[J]. 电子与信息学报, 2010, 32(12): 3013-3017. Zhang Shuang-xi, Sun Guang-cai, Zhou Feng, et al.. A method of based on sub-aperture autofocus to estimate the high-frequency motion error and compensation[J]. Journal of Electronics & Information Technology, 2010, 32(12): 3013-3017.(  1) 1) |
| [22] | 孟大地, 丁赤飚. 一种用于条带式SAR的自聚焦算法[J]. 电子与信息学报, 2005, 27(9): 1349-1352. Meng Da-di and Ding Chi-biao. A new approach to auto-focus consideringstrip map SAR [J]. Journal of Electronics & Information Technology, 2005, 27(9): 1349-1352.(  1) 1) |


