重叠子孔径算法[1](Overlapped Subaperture Algorithm, OSA)是一种高分辨率合成孔径雷达(Synthetic Aperture Radar, SAR)成像算法。OSA在时域对方位向回波信号进行重叠子孔径划分,然后在子孔径内与子孔径间的多次处理过程中引入误差补偿因子,完成方位向的相位误差补偿及距离向与方位向的耦合误差补偿,生成高分辨率雷达图像。OSA成像中对子孔径进行压缩处理后,可以得到每个子孔径的方位向粗分辨率信息,这时子孔径内处于图像域、子孔径间处于时域,这种既在图像域又在时域是OSA独有的特点,利用这一特点可以采用图像域的粗分辨率信息,在成像过程中补偿子孔径间时域的相位误差。OSA与距离多普勒(Range Doppler, RD)算法、线性调频变标 (Chirp Scaling, CS)算法相比,通过在方位向的分块处理能够降低对存储量的需求、采用方位向的子孔径内与子孔径之间的短长度快速傅里叶变换(FFT)有效降低了运算量,更加适合于机载SAR实时成像。
文献[2, 3, 4, 5]针对去斜接收的聚束SAR系统提出了能够校正空变相位误差的OSA算法,可根据雷达系统参数与姿态/位置测量参数实时计算相位补偿因子,有效解决了图像的几何失真与图像空变散焦问题,并实际应用到Lynx型无人机载SAR雷达实时成像处理器中[6]。文献[7, 8, 9, 10, 11]建立了极坐标下的聚束SAR几何模型,对聚束工作模式下的OSA成像算法进行了研究。
OSA算法大部分应用于去斜接收的聚束SAR系统,但是去斜技术限制了SAR系统的条带宽度,无法获取地面的大面积测绘范围;另外条带SAR是成像系统中常用的一种工作模式,其应用更简便直观,因此是SAR系统的基本工作模式。
本文重点提出了基于距离向脉冲压缩体制的机载条带OSA实时成像算法,该算法可应用于未采用去斜接收技术的条带SAR系统,可高效地得到条带模式图像。本文首先分析了条带模式SAR几何关系,然后给出了接收端去斜与非去斜时的SAR回波模型,针对非去斜接收系统对距离向脉冲压缩体制的OSA成像流程进行了详细的数学推导与说明,给出了算法的运算量、存储量与有效成像范围,最后通过对点目标仿真数据与实际回波数据的处理对算法时效性进行了验证。
2 脉冲压缩体制条带SAR的原始数据回波基于去斜接收的聚束式SAR OSA成像算法在文献[3]中有详细介绍,其简要描述见附录。本文基于脉冲压缩的机载条带SAR系统提出了OSA实时成像算法,本节主要描述脉冲压缩体制条带SAR的原始数据回波模型。
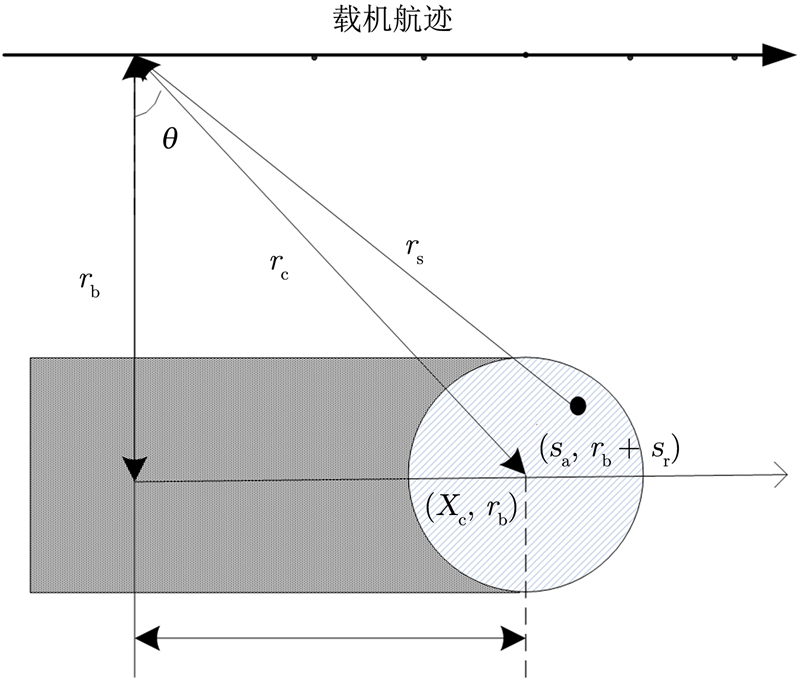
图 1为SAR几何关系示意图。在图 1中,rb为天线波束中心到地面的垂直距离;rs为平台到点目标的瞬时距离;天线的波束中心指向(Xc,rb)处;在(sa,rb+sr)处有一个点目标;飞机位置为x。当Xc=0时,是理想的正侧视条带SAR模式,雷达天线波束中心保持与飞行航迹垂直,均匀照射地面。本文主要讨论正侧视情况。
|
图 1 SAR几何关系示意图 Fig.1SAR geometry |
雷达发射的线性调频信号遇到点目标后反射回雷达,SAR接收到的回波信号为:
| ${X_{\rm{R}}}(t, n) = \cos \left( {2\pi {{f_n}}\left( {t - \frac{{2{r_{\rm{s}}}}}{{\rm{c}}}} \right) + \mathrm{\pi} {{k_n}}{{\left( {t - \frac{{2{r_{\rm{s}}}}}{{\rm{c}}}} \right)}^2}} \right)$ | (1) |
其中:t为时间变量,c为光速,rs为点目标与雷达之间的斜距,fn:第n个雷达脉冲发射信号的中心频率,一般情况下每个脉冲发射的信号中心频率不变均为f0, kn:第n个雷达脉冲发射信号的调频斜率,一般情况下为定值k。
接收端的本振信号为:
| $X_{{\rm{LO}}} (t, n) = \exp \left( { - {\rm{j}}2{\rm{\pi}} f_0 \left( {t - \frac{{2r_{\rm{b}} }}{{\rm{c}}}} \right)} \right)$ | (2) |
其中2rb/c为回波起始采样时间,在SAR系统中为一个固定值,一般取为测绘带起始点或中心点。
将回波信号与参考函数混频后得到:
| $ X_{\rm{v}} (t, n) = \exp \left\{ { {\rm{j}}2{\rm{\pi}} f_0 \left( {\frac{{2r_{\rm{b}} }}{{\rm{c}}} - \frac{{2r_{\rm{s}} }}{{\rm{c}}}} \right)} \right. \left. {+ {\rm{j}}{\rm{\pi}} k\left( {t - \frac{{2r_{\rm{b}} }}{{\rm{c}}} + \frac{{2r_{\rm{b}} }}{{\rm{c}}} - \frac{{2r_{\rm{s}} }}{{\rm{c}}}} \right)^2 } \right\} $ | (3) |
若令${T_{\rm{s}}}{F_{\rm{i}}} = t - \frac{{2{r_{\rm{b}}}}}{{\rm{c}}}$,其中$ - F/2 + 1 \le F_{\rm{i}} \le F/2 $,Ts为采样间隔,Fi为距离向采样点序列编号,F为距离向采样总点数,则SAR原始回波为:
| $X_{\rm{v}} (F_{\rm{i}} , n) = \exp \left\{ {{\rm{j}} \frac{{4{\rm{\pi}} }}{\lambda }\left( {r_{\rm{b}} - r_{\rm{s}} } \right) } \right. \left. { + {\rm{j}} {\rm{\pi}} k\left[ {T_{\rm{s}} F_{\rm{i}} + \frac{2}{{\rm{c}}}\left( {r_{\rm{b}} - r_{\rm{s}} } \right)} \right]^2 } \right\}$ | (4) |
其中λ为雷达发射信号波长。
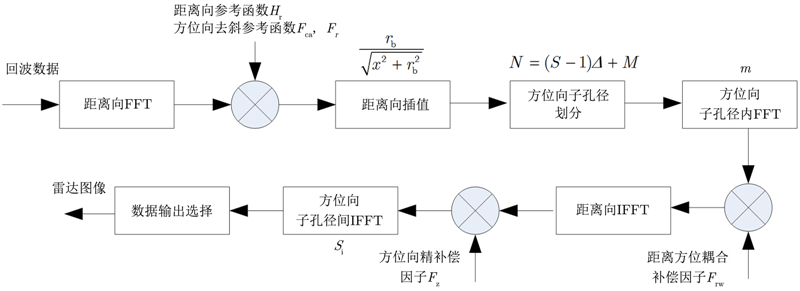
3 脉冲压缩体制条带SAR的OSA成像方法脉冲压缩方式有两种,分别为相关法与去斜法。在去斜体制下,根据SAR回波模型,利用去斜法得到距离向信息。而在非去斜接收的机载SAR系统中,发射较宽线性调频信号以获取高分辨率,若在视频数字域采用去斜法会在频域产生混叠,因此一般采用相关法进行脉冲压缩。采用相关法实现脉冲压缩时,需要把信号FFT变换到频域,将信号频域与含有2次共轭相位的频域滤波器进行复乘,再IFFT变换到时域。将脉冲压缩与方位向OSA处理相结合,SAR成像流程具体可以表示为图 2。
|
图 2 OSA算法应用于条带SAR距离向脉冲压缩的流程示意图 Fig.2 Processing flow of OSA for range pulse compression strip SAR |
OSA应用于距离向脉冲压缩的条带SAR的具体流程为:首先将距离向信号变换为频域,在频域与距离向参考函数、方位向去斜函数复乘,接着在距离向进行插值,然后将去斜后的方位向数据划分为多个重叠的子孔径,再对每个子孔径的方位向进行FFT变换即方位向第1级滤波粗处理。子孔内的方位向处理完毕后,可以得到方位向的粗分辨率信息,利用该信息计算得到每个子孔径的距离方位耦合补偿因子,对每个子孔径进行距离方位耦合补偿,补偿后完成距离向IFFT,由此完成了每个子孔径的距离向脉冲压缩与方位向粗分辨率成像,恢复了每个子孔径内的距离方位信息,得到每个子孔径的图像。利用子孔径的图像信息计算得到方位向精补偿因子,补偿方位向冗余的1次、2次空变相位误差,得到方位向精分辨率图像。最后对方位向数据进行输出选择,去掉重叠部分的图像并进行幅度调制调整。以下对具体实现步骤进行详细说明。
3.1 距离向FFT与方位向去斜对条带SAR回波进行距离向FFT,变换到距离向频域,其频域表达式为:
| $ Y_{f} \left( {f, x} \right) = P(f)\exp \left\{ { - {\rm{j}} \frac{{4{\rm{\pi}} }}{{\rm{c}}}f\left( {r_{\rm{s}} - r_{\rm{b}} } \right)} \right\} \cdot \exp \left\{ { - {\rm{j}}\frac{{4{\rm{\pi}} }}{\lambda }\left( {r_{\rm{s}} - r_{\rm{b}} } \right)} \right\}$ | (5) |
其中P(f)为线性调频信号$\exp \left\{ {{\rm{j}}{{π}} k{t^2}} \right\}$的频率特性。定义去斜参考函数为Fca与Fr分别为:
| ${F_{{\rm{ca}}}} = \exp \left\{ {{\rm{j}}\frac{{4{\rm{\pi}} }}{\lambda }{r_{{\rm{ref}}}}} \right\}$ | (6) |
| ${F_{\rm{r}}} = \exp \left\{ {{\rm{j}}\frac{{4{\rm{\pi}} }}{\lambda }\frac{f}{{{f_0}}}{r_{{\rm{ref}}}}} \right\}$ | (7) |
其中${r_{{\rm{ref}}}} = \sqrt {{x^2} + r_{\rm{b}}^2}$, rref是场景中心点斜距的精确表达式。定义Yc(f, x)为这两个参考函数与距离向匹配滤波参考函数乘积,具体表示为:
| ${Y_{\rm{c}}}\left( {f, x} \right) = {P^ * }\left( f \right) \cdot \exp \left\{ {\rm{j}} {\frac{{4{\rm{\pi}} }}{\lambda }\left( {1 + \frac{f}{{{f_0}}}} \right)\sqrt {{x^2} + r_{\rm{b}}^2} } \right\}$ | (8) |
SAR回波数据在距离向频域乘以参考函数Yc(f, x)后,忽略固定相位后变为:
| $Y\left( {f, x} \right) = {\left| {P\left( f \right)} \right|^2} \cdot \exp - {\rm{j}}\frac{{4{\rm{\pi}} }}{\lambda }\left[ {\left( {1 + \frac{f}{{{f_0}}}} \right)\frac{{{r_b}}}{{\sqrt {{x^2} + r_{\rm{b}}^2} }}} \right. \left( {\frac{{ - x}}{{{r_{\rm{b}}}}}{s_{\rm{a}}} + {s_{\rm{r}}} + {\varepsilon _{{\rm{r}}0}} + {\varepsilon _{{\rm{r}}1}}x + {\varepsilon _{{\rm{r}}2}}{x^2}_{\mathop {_{}}\limits_{_{}} }^{\mathop {}\limits^{_{}} }} \right)\left. {\mathop {_{}}\limits_{_{}} }^{\mathop {}\limits^{_{}} } \right]$ | (9) |
距离向频域经过插值后,写成离散形式:
| $Y\left( {i, x} \right) = {\left| {P\left( f \right)} \right|^2} \cdot \exp - {\rm{j}}\left[{\left( {{k_0} + i \cdot dk} \right)\left( {\frac{{ - x}}{{{r_{\rm{b}}}}}{s_{\rm{a}}} + {s_{\rm{r}}} + {\varepsilon _{{\rm{r}}0}} + {\varepsilon _{{\rm{r}}1}}x + {\varepsilon _{{\rm{r}}2}}{x^2}} \right)} \right]$ | (10) |
其中$ - I/2 + 1 \le i \le I/2$ ,其中i为距离向频域插值后离散化序列索引,I为距离向采样总点数,εr0,εr1与εr2分别是rref关于sa与sr在(0, 0)处泰勒级数展开后$x^0$,$x^1$与$x^2$系数,$i \cdot dk = \frac{{4{\rm{\pi}} }}{\lambda }\frac{f}{{{f_0}}}\frac{{{r_b}}}{{\sqrt {{x^2} + r_{\rm{b}}^2} }}$, ${k_0} = \frac{{4{\rm{\pi \mathop {}\limits^{\mathop {}\limits^{} } }} }}{\lambda }\frac{{{r_b}} }{{\sqrt {{x^2} + r_{\rm{b}}^2} }}$。
3.2 子孔径划分与方位向FFT将方位向位置x写成离散化形式,按照图3在方位向进行子孔径划分。假设全孔径总长度为N点,划分为S个子孔径,每个子孔径长度为M点,相邻子孔径间重叠点数为)$\left( {M - \Delta } \right)$个,则有:

|
图 3 子孔径划分示意图 Fig.3 Aperture divided into subapertures |
| $N = (S - 1)\Delta + M$ | (11) |
子孔径划分大小的因素与子孔径重叠率、第1级粗分辨率有关。子孔径的重叠率即$M/\Delta$,为抑制信号旁瓣一般取为2~3[1, 2]。子孔径长度的选取还受到第1级粗分辨率的限制,具体详见为式(16)和(29)。通过子孔径划分,数据变成了N个2维矩阵,构成了一个关于i, si, m的3维数据矩阵,具体表示为:
| $\begin{aligned} Y\left( {i, m, {s_{\rm{i}}}} \right) = &{\left| {P\left( f \right)} \right|^2} \cdot \exp \left\{ { - {\rm{j}}{k_0}\left( { + {s_{\rm{r}}} + {\varepsilon _{{\rm{r}}0}}} \right)} \right\}\\ & \cdot \exp \left\{ { - {\rm{j}}\left( {i \cdot dk} \right)\left[\begin{array}{l} {s_{\rm{r}}} + {\varepsilon _{{\rm{r}}0}} - \frac{{{s_{\rm{a}}}dx}}{{{r_{\rm{r}}}}}\Delta {s_{\rm{i}}} + {\varepsilon _{{\rm{r}}1}}\Delta {s_{\rm{i}}}dx + {\varepsilon _{{\rm{r}}2}}{\Delta ^2}{s_{\rm{i}}}_{}^2d{x^2} \end{array} \right]} \right\}\\ & \cdot \exp \left\{ { - {\rm{j}}{k_0}\left[{ - \frac{{{s_{\rm{a}}}dx}}{{{r_{\rm{b}}}_{}}}\Delta {s_{\rm{i}}} + {\varepsilon _{{\rm{r}}1}}\Delta {s_{\rm{i}}}dx + {\varepsilon _{{\rm{r}}2}}{\Delta ^2}{s_{\rm{i}}}_{}^2d{x^2}} \right]} \right\}\\ & \cdot \exp \left\{ { - \left( {{k_0} + i \cdot dk} \right)\left[\begin{array}{l} - \frac{{dx \cdot {s_{\rm{a}}}}}{{{r_{\rm{b}}}}}m + {\varepsilon _{{\rm{r}}1}}mdx + {\varepsilon _{{\rm{r}}2}}{m^2}d{x^2} + 2{\varepsilon _{{\rm{r}}2}}m\Delta {s_{\rm{i}}}d{x^2} \end{array} \right]} \right\} \end{aligned}$ | (12) |
其中si为子孔径内采样点的索引,-S/2+1<si< S/2, m为子孔径序列的索引,-M/2+1<m< M/2。
式(12)的第4项指数项是关于子孔径内序列m的函数,若2次相位小于${{π}}$/2,具体表示为:
| $\left| {\left( {{k_0} + i \cdot dk} \right){\varepsilon _{{\rm{r}}2}}{m^2}d{x^2}} \right| \le \frac{\pi }{2}$ | (13) |
则可以忽略关于m的2次项,对变量m做FFT变换,FFT变换后得到子孔内方位向粗分辨率图像,具体表示为:
|
|
(14) |
其中${{\mathop{\rm csinc}\nolimits} _M}( \cdot )$定义为:
| ${{\mathop{\rm csinc}\nolimits} _M}(x) \equiv \frac{{\sin (x)}}{{\sin (x/M)}}{e^{ - {\rm{j}}\frac{x}{M}}}$ | (15) |
通过对变量m的FFT,得到了子孔内压缩后对sa的第1次估计值${\widehat{s} _{{\rm{a}},1}} $,具体可表示为:
| $\mathop {{s_{{\rm{a}}, 1}}}\limits^ \wedge = - \frac{{2\pi {u_1}{r_{\rm{b}}}}}{{M{k_0}dx}} + \frac{{i \cdot dk}}{{{k_0}}}{s_{\rm{a}}} + {r_{\rm{b}}}\left( {1 + \frac{{i \cdot dk}}{{{k_0}}}} \right)\left( {{\varepsilon _{{\rm{r}}1}} + 2{\varepsilon _{{\rm{r}}2}}dx\Delta {s_{\rm{i}}}} \right)$ | (16) |
子孔内方位向粗分辨率为:
| $\mathop {{\rho _{{\rm{a}}, 1}}}\limits^{} = \frac{{2\pi {r_{\rm{b}}}}}{{M{k_0}dx}}$ | (17) |
由式(16)可以看到,每个子孔径的压缩峰值位置在随子孔径si,距离向i迁移,为了能够得到精聚焦图像,需要对迁移量进行限制,一般将这个迁移量限制在半个粗分辨率单元以内,具体可以表示为::
| $\left| {\frac{{i \cdot dk}}{{{k_0}}}{s_{\rm{a}}} + {r_{\rm{b}}}\frac{{i \cdot dk}}{{{k_0}}}{\varepsilon _{{\rm{r}}1}} + {r_{\rm{b}}}\left( {1 + \frac{{i \cdot dk}}{{{k_0}}}} \right)\left( {2{\varepsilon _{{\rm{r}}2}}dx\Delta {s_{\rm{i}}}} \right)} \right| \le \frac{{\mathop {{\rho _{{\rm{a}}, 1}}}\limits^{} }}{2}$ | (18) |
根据方位向粗处理结果,可以求出关于sa的第1次估计值${{\widehat{s}} _{{\rm{a}},1}}$。由此可以求出${\mathop \varepsilon \limits^{} _{{\rm{r}}0}}$, ${\mathop \varepsilon \limits^{} _{{\rm{r}}1}}$, ${\mathop \varepsilon \limits^{} _{{\rm{r}}2}}$的第1次估计值${{\widehat{\varepsilon}} _{{\rm{r}}0,1}}$, ${{\widehat{\varepsilon}} _{{\rm{r}}1,1}}$, ${{\widehat{\varepsilon}} _{{\rm{r}}2,1}}$,通过这些估计值可以算得距离方位的耦合补偿向量:
| ${F_{{\rm{rw}}}}\left( {i, {u_1}, {s_{\rm{i}}}} \right) = \exp \left\{ {\rm{j} \cdot i \cdot dk\left( {{{\mathop \varepsilon \limits^ \wedge }_{_{{\rm{r}}0, 1}}} - \frac{{{{\mathop s\limits^ \wedge }_{{\rm{a}}, 1}}dx}}{{{r_{\rm{b}}}}}\Delta {s_{\rm{i}}} + {{\mathop \varepsilon \limits^ \wedge }_{{\rm{r}}1, 1}}\Delta {s_{\rm{i}}}dx + {{\mathop \varepsilon \limits^ \wedge }_{{\rm{r}}2, 1}}{\Delta ^2}{s_{\rm{i}}}_{}^2d{x^2}} \right)} \right\}$ | (19) |
补偿后对变量i做IFFT变换得到:
|
|
(20) |
由此恢复出距离向信息,得到了每个子孔径的图像,其中距离向为高分辨率、方位向为粗分辨率。由式(20)可以看到距离向的位置随si发生迁移,若迁移量能够满足半个距离分辨单元,则迁移可忽略,具体表示为:
| $\left| { - \frac{{\left( {{s_{\rm{a}}} - {{\mathop s\limits^ \wedge }_{{\rm{a}}, 1}}} \right)}}{{{r_{\rm{b}}}}}\Delta {s_{\rm{i}}}dx + \left( {{\varepsilon _{{\rm{r}}1}} - {{\mathop \varepsilon \limits^ \wedge }_{{\rm{r}}1, 1}}} \right)\Delta {s_{\rm{i}}}dx + \left( {{\varepsilon _{{\rm{r}}2}} - {{\mathop \varepsilon \limits^ \wedge }_{{\rm{r}}2, 1}}} \right){\Delta ^2}{s_{\rm{i}}}_{}^2d{x^2}} \right| \le \frac{{{\rho _{\rm{r}}}}}{2}$ | (21) |
若式(21)能够满足,则距离向的位置估计值$\widehat{s}_{\rm{r}}$可以表示为:
| $\mathop {{s_{\rm{r}}}}\limits^ \wedge = \frac{{2\pi v}}{{I \cdot dk}} - \left( {{\varepsilon _{{\rm{r}}0}} - {{\mathop \varepsilon \limits^ \wedge }_{{\rm{r0}}{\rm{1}}}}} \right)$ | (22) |
根据每个子孔径图像,可以求出sr的估计值${\widehat{s} _{{\rm{r}},1}}$,进一步求出${\mathop \varepsilon \limits^{} _{{\rm{r}}0}}$, ${\mathop \varepsilon \limits^{} _{{\rm{r}}1}}$, ${\mathop \varepsilon \limits^{} _{{\rm{r}}2}}$的第2次估计值${\widehat{\varepsilon} _{{\rm{r}}0,2}}$, ${\widehat{\varepsilon} _{{\rm{r}}1,2}}$, ${\widehat{\varepsilon} _{{\rm{r}}2,2}}$ ,利用第2次估计值算得第2次方位向滤波处理前所需的误差补偿向量,表示为:
| ${F_{\rm{z}}}\left( {v, {u_1}, {s_{\rm{i}}}} \right) = \exp \left\{ {\rm{j} \cdot {k_0}\left( { - \frac{{{{\mathop s\limits^ \wedge }_{{\rm{a}}, 1}}}}{{{r_{\rm{b}}}}}\Delta {s_{\rm{i}}}dx + {{\mathop \varepsilon \limits^ \wedge }_{{\rm{r}}1, 2}}\Delta {s_{\rm{i}}}dx + {{\mathop \varepsilon \limits^ \wedge }_{{\rm{r}}2, 2}}{\Delta ^2}{s_{\rm{i}}}_{}^2d{x^2}} \right)} \right\}$ | (23) |
补偿后若关于s_{\rm{i}} $的2次相位小于${{π}}/ 2 $,即满足:
| $\left| {{k_0}\left( {{\varepsilon _{{\rm{r}}2}} - {{\mathop \varepsilon \limits^ \wedge }_{{\rm{r}}2, 2}}} \right){\Delta ^2}{s_{\rm{i}}}_{}^2d{x^2}} \right| \le \frac{\rm{\pi} }{2}$ | (24) |
则可以忽略2次相位,对si进行FFT变换后得到:
|
|
(25) |
式(25)为正侧视条带SAR模式下的图像重建,其中方位向输出为:
| ${\widehat s _{{\rm{a}}, 2}} = - \frac{{\lambda {r_{\rm{b}}}({u_2} - S/2)}}{{2S\Delta dx}} - \frac{{\lambda {r_{\rm{b}}}({u_1} - M/2)}}{{2Mdx}} + {r_{\rm{b}}}\left( {{\varepsilon _{{\rm{r}}1}} - {\widehat \varepsilon _{{\rm{r}}1, 2}} } \right)$ | (26) |
图像的距离向分辨率由发射信号带宽决定,图像的方位向分辨率为:
| ${\rho _{{\rm{a}}, 2}} \approx \frac{{\lambda {r_{\rm{b}}}}}{{2S\Delta dx}}$ | (27) |
式(25)是一个关于3维向量(u1, u2, v)的数学表达式,而雷达图像实际上是个2维图像,因此需要将式(24)的方位向进行数据输出选择,即将方位向数据进行重排。v对应的是距离向,(u1, u2)对应的是方位向,因此数据输出选择是针对(u1, u2)进行的数据重排,数据重排的原则与子孔径划分方法一致。另外在方位向经过了两次FFT运算,第1次FFT运算即粗处理过程中引入了幅度调制,影响了第2次FFT运算即精处理输出的幅度,导致了精处理输出后的数据有明暗“条纹”。为保证最终图像幅度一致性,在方位向精处理完毕后需要对幅度进行校正,幅度校正因子与sinc函数幅度一致。
4 算法性能分析 4.1 运算量与存储量分析以一个大小为M×N点的SAR原始数据块为例,其中距离向点数为M,取值为4096,方位向点数为N,取值为4096点。采用本方法进行成像的运算量如表 1所示。其中长度为N的FFT或IFFT的浮点运算(Floating Point Operations, FLOP)为5Nlog2(N),一次复乘需要6个FLOP。OSA的总运算量与RD,CS的5.61G,4.05G[12]相比,分别下降了30%与5%。在实际系统处理时,一般脉冲重复频率比是方位向多普勒带宽的2倍以上,这样在第1级子孔径处理完毕后冗余点会达到子孔径的一半,去掉冗余点后,OSA运算量还会进一步降低。
| 表 1 脉冲压缩条带SAR的OSA运算量估计 Tab.1 Computation load of OSA for pulse compression strip SAR |
由于OSA将方位向数据划分多个小数据块,每次仅针对小数据块进行操作,因此OSA应用于高速实时并行处理时对数据存储量的要求方面具有很大的优势。对一个16384×16384点的数据块进行实时成像时,降4倍降采样滤波,成像中距离向有效点输出为12000点,图像采用16bit量化。方位向划分S=256个子孔径,每个子孔径长度为M=32,Δ=16点,第1级子孔径处理完毕后去掉冗余点保留16点。分别采用RD,CS,OSA成像时需要的存储量如表 2所示。
| 表 2 不同实时成像算法的存储量对比 Tab.2 Data storage of different real-time imaging algorithm |
由表 2中可以看到,相对比CS方法,OSA对转置存储容量要求降低一倍以上;相比RD算法,转置存储量基本相当,但是从运算量、性能上要优于RD。由于进行了子孔径划分,第1次和第2次转置存储量很小,在实时处理时,利用高速数字信号处理芯片内部的存储空间就能够实现转置,降低了对硬件资源的要求,还便于运算与数据读取的流水设计。因此在高分辨率处理时,从处理性能、运算量和存储量几个方面考虑,OSA是一种比较优化的实时处理方法。
4.2 成像范围分析式(13),式(18),式(21)与式(24)为本文算法对成像范围的限制,根据计算比较分析,得到最终对方位向Dx,距离向成像范围Dy与方位向第1级粗分辨率单元的成像限制,分别为:
| ${D_{\rm{x}}} \le {\rho _{{\rm{a}}, 1}}{\rho _{\rm{r}}}\frac{4}{\lambda }$ | (28) |
| ${D_{\rm{y}}} \le \sqrt {\frac{{\mathop 4\limits^{} }}{\lambda }{\rho _{{\rm{a}}, 1}}{\rho _{{\rm{a}}, 2}}\frac{{{r_{\rm{b}}}}}{{\left( {1 + \frac{{k{T_{\rm{s}}}I}}{{2{f_0}}}} \right)}}}$ | (29) |
| ${\rho _{{\rm{a}}, 1}} \le \frac{4}{\lambda }{\rho _{\rm{r}}}{\rho _{{\rm{a}}, 2}}$ | (30) |
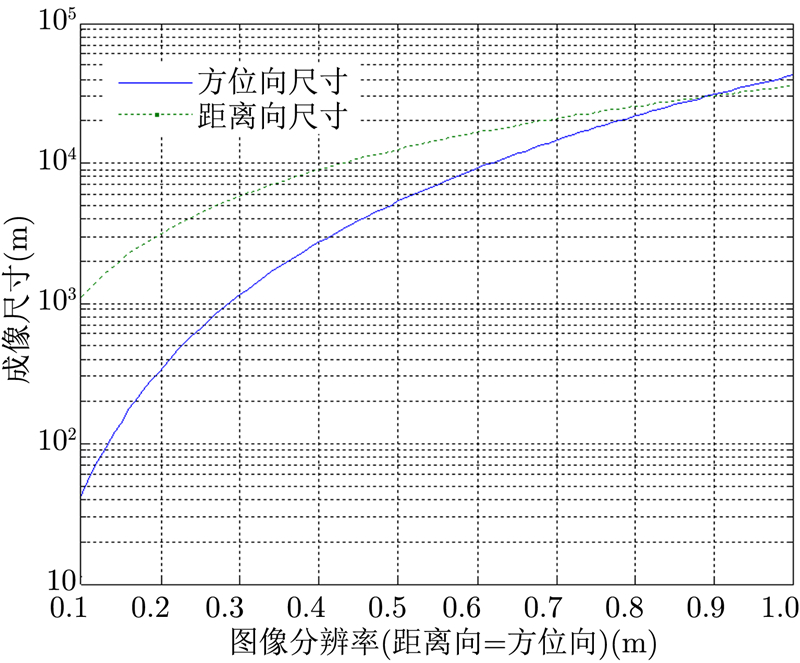
图 4为本文算法中成像范围与图像分辨率的关系,在Ku波段时,若要得到0.3 m分辨率,方位向成像尺寸为1.2 km,距离向尺寸大于8 km,已经能够满足大部分实际机载SAR系统实时处理的要求。通过成像范围与方位向第1级粗分辨率限制的分析,可以指导子孔径的具体划分。
|
图 4 OSA算法的成像范围 Fig.4 Scene diameter limits for OSA |
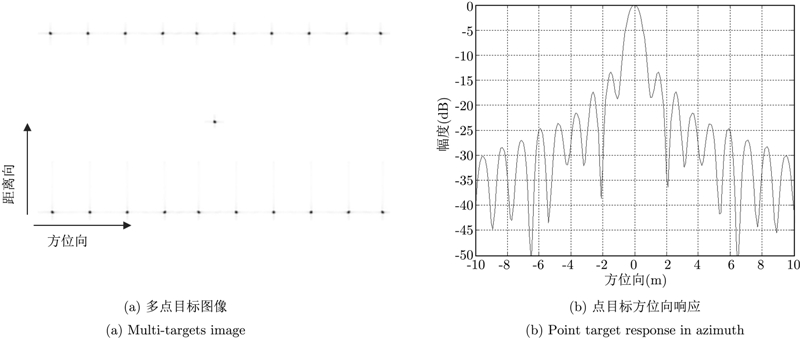
仿真中共放置21个点目标,在场景中心有1个点目标,其余的20个点目标围绕中心点目标组成一个矩形场景,相邻点方位向间距为100 m,距离向间距为400 m,水平方向为方位向,垂直方向为距离向。用本文算法重建图像后,不仅图像中心处的点聚焦良好图像没有形变,而且图像边缘处的点聚焦效果也满足分辨率要求,具体图 5(a),5(b)所示。SAR系统参数与成像参数见表 3。方位向子孔径划分时,重叠率选取为2,根据式(17),式(30)计算得到子孔径长度需要大于12,在实际的SAR实时处理系统中,一般FFT的长度取为2n,结合实时处理效率考虑,子孔径长度选取为64,子孔径个数选为512个。选取了场景中心与边缘共5个点进行了成像评估,经测量所有点的3 dB宽度、积分旁瓣比与峰值旁瓣比均达到指标要求。其中点目标1,点目标2,点目标4与点目标5为图像最边缘处的4个点,分别位于图像左上、右上、左下与右下角,点目标3为场景中心处的点目标。
|
图 5 点目标仿真结果 Fig.5 Point-targets simulation |
| 表 3 不同实时成像算法的存储量对比 Tab.3 Data storage of different real-time imaging algorithm |
图 6是某无人机载SAR原始数据利用高速实时专用信号处理平台的实时成像结果。SAR系统参数与成像参数与点目标仿真参数相同,具体如表 3所示。通过对实测数据的成像结果表明,实时成像处理速度满足系统实时性要求,成像处理结果满足系统对图像质量的要求。本文描述的适用于距离向脉冲压缩条带SAR的OSA算法能够应用于中小型无人机载SAR系统的实时成像处理器。

|
图 6 某无人机载SAR数据实时成像结果 Fig.6 UAV SAR real-time image |
本文算法在时域将方位向数据划分为多个孔径,更适用于无人机载SAR系统合成孔径时间长的使用条件;本文算法对每个子孔径数据分别处理,有利于并行实现、降低了数据存储与实时信号处理硬件的设备要求同时还便于运动补偿[13],有助于无人机载SAR系统的小型化与轻量化;本文算法中相位误差补偿与成像处理同时完成,直接生成高分辨率图像,具有较高的计算效率;本文算法在脉冲压缩体制下工作,无需在接收端对回波信号进行去斜处理,降低接收端设备的复杂度。但是本文算法也具有一定的局限性,在一定的成像范围内才有效,尤其是在0.1m及以上高分辨率模式时,对成像范围要求较为苛刻,因此为提高高分辨率SAR的成像范围可以进一步考虑多级子孔径的成像方法。
5 结束语本文提出了一种面向距离向脉冲压缩的机载条带SAR重叠子孔径实时成像算法,该算法具有以下特点:(1)雷达数据经过子孔径划分后,在成像过程中可以通过在多普勒域复乘校正因子消除每个子孔径的距离向与方位向耦合,降低了运算复杂度;(2)通过扩展SAR回波模型的泰勒级数展开项数,通过子孔径划分、距离迁移校正因子、精聚焦因子等消除方位向高阶相位误差。与常规接收端去斜聚束SAR系统中的极坐标OSA算法相比,本文算法有如下优势:(1) 可适用于脉冲压缩体制的SAR 系统,获取更高测绘带宽的雷达图像。(2)可适用于条带式SAR工作模式。(3) 可降低实时成像处理中数据存储量与运算量要求,提高了系统硬件并行性。通过对模型分析以及仿真和实测数据的处理验证了该算法的有效性,并在中小型无人机载高分辨率SAR实时成像领域具有广泛的应用前景。
附录:接收端去斜的SAR回波模型与OSA成像方法流程SAR发射一个线性调频信号,接收到的回波信号为:
| ${X_{\rm{R}}}(t, n) = A({r_{\rm{s}}})\cos \left( {2\pi {f_{\rm{n}}}\left( {t - \frac{{2{r_{\rm{s}}}}}{{\rm{c}}}} \right) + \pi {k_{\rm{n}}}{{\left( {t - \frac{{2{r_{\rm{s}}}}}{{\rm{c}}}} \right)}^2}} \right)$ | (A-1) |
其中t为时间变量,c为光速,fn:第n个雷达脉冲发射信号的中心频率, kn:第n个雷达脉冲发射信号的调频斜率。
在接收端的本振信号为:
| ${X_{{\rm{LO}}}}(t, n) = \exp \left\{ { - {\rm{j}}2\pi {f_{\rm{n}}}\left( {t - \frac{{2{r_{{\rm{ref}}}}}}{{\rm{c}}}} \right) - \pi {k_{\rm{n}}}{{\left( {t - \frac{{2{r_{{\rm{ref}}}}}}{{\rm{c}}}} \right)}^2}} \right\}$ | (A-2) |
其中${r_{{\rm{ref}}}} = \sqrt {{x^2} + r_b^2} $
将回波信号与参考函数混频后得到:
| $\begin{aligned} X_{\rm{v}} (t, n) = \exp \left\{ {\rm{j}\frac{2}{{\rm{c}}}\left[ {2{\rm{\pi}} f_{\rm{n}} + 2{\rm{\pi}} k_{\rm{n}} \left( {t - \frac{{2r_{{\rm{ref}}} }}{{\rm{c}}}} \right)} \right]} \right. \left. {\left( {r_{{\rm{ref}}} - r_{\rm{s}} } \right) + \frac{{4{\rm{\pi}} k_{\rm{n}} }}{{{\rm{c}}^2 }}\left( {r_{{\rm{ref}}} - r_{\rm{s}} } \right)^2 } \right\} \\ \end{aligned}$ | (A-3) |
在距离向进行采样,令${T_{\rm{s}}}{F_{\rm{i}}} = t - \frac{{2{r_{{\rm{ref}}}}}}{{\rm{c}}}$。注意在去斜接收时距离向采样时间起始时刻根据雷达位置x而实时改变,由于采用了与方位向相关的去斜参考信号,在模拟接收端实现了距离向和方位向的2维去斜。
由于
${r_{{\rm{ref}}}} - {r_{\rm{s}}} = \sqrt {{x^2} + r_{\rm{b}}^2} - \sqrt {{{\left( {{s_{\rm{a}}} - x} \right)}^2} + {{\left( {{r_{\rm{b}}} + {s_{\rm{r}}}} \right)}^2}} $,混频后的信号可以写为:
| ${X_{\rm{v}}}(i, n) = \exp \left\{ {\rm{j}\frac{2}{{\rm{c}}}\left( {2\rm{\pi} {f_{\rm{n}}} + 2\rm{\pi} \\{k_{\rm{n}}}{T_{\rm{s}}}{F_{\rm{i}}}} \right)\frac{{{r_{\rm{b}}}}}{{\sqrt {{{\left( {ndx} \right)}^2} + r_{\rm{b}}^2} }} \\\cdot \left( {\frac{{ - ndx}}{{{r_{\rm{b}}}}}{s_{\rm{a}}} + {s_{\rm{r}}} + {\varepsilon _{\rm{r}}}} \right) + \frac{{4\rm{\pi} {k_{\rm{n}}}}}{{{{\rm{c}}^2}}}\frac{{{r_{\rm{b}}}}}{{\sqrt {{{\left( {ndx} \right)}^2} + r_{\rm{b}}^2} }} \cdot {\varepsilon _{\rm{p}}}} \right\}$ | (A-4) |
在式(A-4)中认为:
| ${\varepsilon _{\rm{r}}} = {\varepsilon _{{\rm{r}}0}}{x^0} + {\varepsilon _{{\rm{r}}1}}{x^1} + {\varepsilon _{{\rm{r}}2}}{x^2}$ | (A-5) |
| ${\varepsilon _{\rm{p}}} = {\varepsilon _{{\rm{p}}0}}{x^0} + {\varepsilon _{{\rm{p}}1}}{x^1} + {\varepsilon _{{\rm{p}}2}}{x^2}$ | (A-6) |
式(A-4)中可以看到$\frac{{{r_{\rm{b}}}}}{{\sqrt {{{\left( {ndx} \right)}^2} + r_{\rm{b}}^2} }}$影响着距离向、方位向位置sr, sa的压缩输出,因此在接收端去斜时,系统在发射脉冲之间实时改变中心频率、发射信号调频斜率,令:
| ${f_{\rm{n}}} = {f_0}\frac{{\sqrt {{{\left( {ndx} \right)}^2} + r_{\rm{b}}^2} }}{{{r_{\rm{b}}}}}$ | (A-7) |
| ${k_{\rm{n}}} = k\frac{{\sqrt {{{\left( {ndx} \right)}^2} + r_{\rm{b}}^2} }}{{{r_{\rm{b}}}}}$ | (A-8) |
则采样后的雷达回波视频信号最终形式为:
| ${X_{\rm{v}}}(i, n) = \exp \left\{ {\rm{j}\frac{2}{{\rm{c}}}\left( {2\rm{\pi}{f_{\rm{0}}} + 2\rm{\pi} k{T_{\rm{s}}}{F_{\rm{i}}}} \right) \cdot \left( {\frac{{ - ndx}}{{{r_{\rm{b}}}}}{s_{\rm{a}}} + {s_{\rm{r}}} + {\varepsilon _{\rm{r}}}} \right) + \frac{{4\rm{\pi} {k_{}}}}{{{{\rm{c}}^2}}} \cdot {\varepsilon _{\rm{p}}}} \right\}$ | (A-9) |
对式(A-9)中的距离向进行FFT,方位向进行进行OSA处理,就能够得到雷达图像。
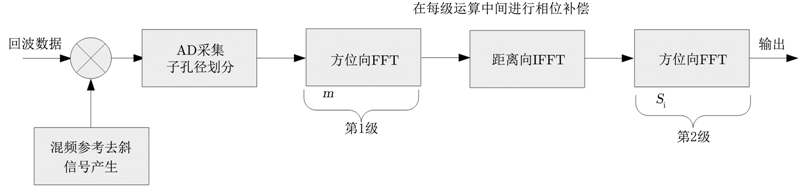
接收端采用一个与发射信号符号相反的本振、调频斜率相反的混频信号与SAR回波信号进行混频,在高频段完成去斜处理。在Lynx系统中不仅要发射中心频率、调频斜率按规律变化的线性调频信号,还要在接收端利用混频信号发生设备,生成中心频率、调频斜率实时变化的本振信号,系统的起始采样时间也实时发生变化。利用这些措施,在接收端完成了距离向、方位向的2维去斜,完成了距离向插值操作,有利于OSA的实时实现、简化了后端实时处理。图 7为基于接收端去斜的OSA成像方法流程图。
|
图 7 基于接收端去斜的OSA成像方法流程图 Fig.7 Processing flow of OSA for dechirp-on-reciever SAR |
| [1] |
Burns B L and Cordaro J T. SAR image formation algorithm that compensates for the spatially variant effects of antenna motion [J] . Proceedings of SPIE, 1994, 2230(4):14-24. ( 2) 2)
|
| [2] |
Burns B L and Cordaro J T. Imaging synthetic aperture radar[P]. United States Patent, 1997, No.5608404. (  2) 2)
|
| [3] |
Doerry A W. Synthetic aperture radar processing with tiered subapertures[J]. Communications and Radar, 1994, 30(4) : 1125-1129( 1) 1)
|
| [4] |
Doerry A W. Synthetic aperture radar processing with polar formatted subapertures[C]. Proceedings of 28th Asilomar Conferrence Signals System Computer, Pacific Grove, CA, 1994:1210-1215. ( 1) 1)
|
| [5] |
Doerry A W. Wavefront curvature limitations and compensation to polar format processing for synthetic aperture radar images[R]. Sandia National Labs, New Mexico, CA, Technical Report, SAND2007-0046, 2007. ( 1) 1)
|
| [6] |
Walker B, Sander G, Thompson M, et al.. A high-resolution, four-band SAR Testbed with real-time image formation[C]. International Geoscience and Remote Sensing Symposium(IGARSS) 1996, Lincoln, NE. 1996(3):1881-1885.( 1) 1)
|
| [7] |
谢冬冬, 禹卫东, 徐峰, 等.利用OSA算法处理条带SAR数据[J].系统工程与电子技术, 2005, 27(6):1003-1006 Xie Dong-dong, Yu Wei-dong, Xu Feng, et al.. OSA algorithm for the processing of stripmap SAR data[J]. Systems Engineering and Electronics, 2005, 27(6): 1003–1006.(  1) 1)
|
| [8] |
Tang Yu, Zhang Bo, Xing Meng-dao, et al.. Azimuth overlapped subaperture algorithm in frequency domain for highly squinted synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10( 4) 692 -696.( 1) 1)
|
| [9] |
唐禹, 邢孟道, 保铮, 等. 基于重叠子孔径极坐标算法的波前弯曲效应的补偿[J]. 电子学报, 2008, 36(6):108-1113 Tang Yu, Xing Meng-dao, Bao Zheng, et al.. Wavefront curvature compensation based on overlapped subaperture polar format algorithm[J]. Acta Electronica Sinica, 2008, 36(6): 1108–1113.(  1) 1)
|
| [10] |
毛新华, 曹海洋, 朱岱寅, 等. 基于先验知识的SAR两维自聚焦算法[J].电子学报, 2013, 41 (6):1041-1047 Mao Xin-hua, Cao Hai-yang, Zhu Dai-yin, et al.. Prior knowledge aided two dimensional autofocus approach for synthetic aperture radar[J]. Acta Electronica Sinica, 2013, 41(6): 1041–1047.(  1) 1)
|
| [11] |
Mao Xin-hua, Zhu Dai-yin and Zhu Zhao-da. Polar format algorithm wavefront curvature compensation under arbitrary radar flight path[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3):526-530( 1) 1)
|
| [12] |
Cumming I G and Wong F H. Digital processing of synthetic aperture radar data[M]. Norwood, MA, Artech House, Inc., 2005: chapter 11.( 1) 1)
|
| [13] |
田雪, 梁兴东, 李焱磊, 等. 基于子孔径包络误差校正的SAR高精度运动补偿方法[J]. 雷达学报, 2014, 3(4):583-590 Tian Xue, Liang Xing-dong, Li Yan-lei, et al.. Highprecision motion compensation method based on the subaperture envelope error correction for SAR[J]. Journal of Radars, 2014, 3(4): 583–590.(  1) 1)
|


