②复旦大学电磁波信息科学教育部重点实验室 上海 200433
②Key Laboratory for Information Science of Electromagnetic Waves (Ministry of Education), Fudan University, Shanghai 200433, China
认知雷达是未来雷达系统发展的重要方向[1]。认知雷达通过对历史和当前环境的检测、分析、学习、推理和规划,可利用相应的结果自适应调整系统的接收和发射信号,使用最适合的系统配置达到与外部环境和目标状态相匹配,可以实现获取最佳的系统性能[2]。作为认知雷达的重要分支,认知跟踪雷达[3]已成为目前的研究热点之一。认知跟踪雷达通过目标状态等先验信息设计发射波形,并从目标和环境的回波中提取出下一时刻信号发射的先验信息,完成新的波形设计,提高目标的跟踪性能。文献[3]系统地介绍了认知跟踪雷达,通过认知波形选择,以目标跟踪误差最小为准则,利用容积卡尔曼滤波实现了目标认知跟踪。文献[4]利用正交频分复用(OFDM)信号,从优化后验克拉美罗界的角度出发,完成对OFDM信号子载频系数的设计,实现了多径环境下目标的跟踪。文献[5]通过优化认知雷达网络的天线选择和功率分配,应用两步贪婪算法,完成了认知雷达网络多目标跟踪问题。
在多目标跟踪情况下,目标的状态信息可以用该时刻时延和多普勒频移唯一确定,因此,本文提出了一种基于时延-多普勒的网格搜索方法,实现了目标回波信号的稀疏表示,进而证明了压缩感知理论能够应用于目标跟踪过程中。压缩感知理论[6, 7, 8] (Compressed Sensing,CS)可以充分利用回波量测信号的稀疏性或可压缩性,采用远低于两倍信号频率的采样速率实现对信号的采样和重构,突破了传统奈奎斯特采样定理的限制。通过将压缩感知理论引入到多目标跟踪算法中,可以大大降低回波信号的采样率和数据处理。
本文提出了一种基于压缩感知的多目标认知雷达跟踪方法,将压缩感知理论引入到认知雷达跟踪算法中。首先对多目标跟踪问题进行了建模,在此基础上,通过构建时延和多普勒网格,完成了目标的量测模型稀疏表示,然后结合粒子群优化粒子滤波算法对目标的状态进行实时估计,在此基础上推导了系统跟踪精度的后验克拉美罗界(Posterior Cramér-Rao Bounds,PCRB),并基于PCRB准则提出了相应的发射波形设计方法。最后,仿真结果验证了与传统方法相比,本文方法能够在降低采样率和数据量的条件下,较好地完成对运动目标的跟踪。
2 跟踪问题建模 2.1 量测模型在目标跟踪过程中,相对于线性调频信号,非线性调频波形具有较强的低截获性能力和更好的距离多普勒耦合特性[9],因此,非线性调频波形能够更好地满足雷达跟踪器的要求,从而提供更好的跟踪性能[10]。
本文采用一种非线性调频波形$\frac{\text{ }}{{}}$广义调频(Generalized Frequency Modulation,GFM)波形作为发射信号,假设${{f}_{\text{c}}}$为载频,则雷达的发射信号为:
| ${{S}_{\text{T}}}(t)=\sqrt{2}\operatorname{Re}\left\{ \tilde{s}(t)\exp \left( 2\pi {{f}_{\text{c}}}t \right) \right\}$ | (1) |
| $\tilde{s}(t)={{\left( \pi {{\lambda }^{2}} \right)}^{-1/4}}\exp \left( -\left( 1/2{{\lambda }^{2}}-jb \right){{t}^{2}} \right)$ | (2) |
| $\begin{align} & {{S}_{\text{R}}}(t)=\sqrt{2}\operatorname{Re}\left\{ \left[ \sum\limits_{m=1}^{M}{\zeta _{k}^{m}\tilde{s}\left( t-\tau _{k}^{m} \right)} \right. \right. \\ & \left. \left. {{ }^{^{^{^{^{{}}}}}}} \qquad \quad \ \cdot {{e}^{j2\pi \nu _{k}^{m}\left( t-\tau _{k}^{m} \right)}}+w\left( t \right) \right]{{e}^{j2\pi {{f}_{\text{c}}}t}} \right\} \\ \end{align}$ | (3) |
| $r(t)=\sum\limits_{m=1}^{M}{\zeta _{k}^{m}\tilde{s}\left( t-\tau _{k}^{m} \right){{e}^{j2\pi \nu _{k}^{m}\left( t-\tau _{k}^{m} \right)}}}+w(t)$ | (4) |
以${{t}_{s}}\text{=1/2}B\text{=}T\text{/}N$为采样间隔对回波信号进行采样,整理得到:
| $\begin{align} & r\left( n,\tau _{k}^{m},\nu _{k}^{m} \right)=\sum\limits_{m=1}^{M}{\zeta _{k}^{m}\phi \left( n,\tau _{k}^{m},\nu _{k}^{m} \right)+w\left( n{{t}_{s}} \right)}, \\ & \qquad \qquad \qquad \quad n=1,2,\cdots ,N \\ \end{align}$ | (5) |
| $\mathbf{w}=\left[ w\left( {{t}_{s}} \right) w\left( 2{{t}_{s}} \right) \cdots w\left( N{{t}_{s}} \right) \right]_{_{1\times N}}^{\text{T}}$ |
| $\begin{align} & \qquad \qquad \qquad \quad \Phi ={{\left[ \begin{matrix} \phi \left( 1,\tau _{k}^{1},\nu _{k}^{1} \right) & \cdots & \phi \left( 1,\tau _{k}^{M},\nu _{k}^{M} \right) \\ \vdots & \ddots & \vdots \\ \phi \left( N,\tau _{k}^{1},\nu _{k}^{1} \right) & \cdots & \phi \left( N,\tau _{k}^{M},\nu _{k}^{M} \right) \\ \end{matrix} \right]}_{N\times M}} \\ & \qquad \qquad \qquad \quad \ \zeta =\text{diag}{{\left[ \zeta _{k}^{1} \zeta _{k}^{2} \cdots \zeta _{k}^{M} \right]}_{M\times M}} \\ \end{align}$ |
则有:
| $r=\Phi \zeta +w$ | (6) |
假设共有$M$个目标在空间中匀速运动,各个目标之间的运动状态相互独立,令$x_{k}^{m},y_{k}^{m},\dot{x}_{k}^{m}$和$\dot{y}_{k}^{m}$表示第$k$时刻第$m$个目标的位置和速度,用向量$\xi _{k}^{m}={{[x_{k}^{m} y_{k}^{m} \dot{x}_{k}^{m} \dot{y}_{k}^{m}]}^{\text{T}}}$表示该时刻第$m$个目标的运动状态。则目标的状态方程可以表示为:
| $\xi _{k+1}^{m}=H\xi _{k}^{m}+u_{k}^{m}$ | (7) |
当目标沿着线性轨迹运动时,可以将状态矩阵H表示为:
| $H=\left[ \begin{align} & 1 \quad 0 \quad \Delta t \quad 0 \\ & 0 \quad \text{1} \quad \text{0 } \quad \Delta t \\ & 0 \quad 0 \quad 1 \quad 0 \\ & 0 \quad 0 \quad 0 \quad 1 \\ \end{align} \right]$ | (8) |
| ${{\Sigma }_{e}}=\varepsilon \left[ \begin{align} & \Delta {{t}^{3}}/3 \quad \quad 0 \quad \quad \Delta {{t}^{2}}/2 \quad \quad 0 \\ & \quad 0 \quad \quad \Delta {{t}^{3}}/3 \quad \quad 0 \quad \quad \Delta {{t}^{2}}/2 \\ & \Delta t/2 \quad \quad \ \ 0 \quad \quad \ \ \Delta t \quad \quad \quad 0 \\ & \quad 0 \quad \quad \Delta t/2 \quad \quad \ \ 0 \quad \quad \quad \Delta t \\ \end{align} \right]$ | (9) |
压缩感知理论是一种全新的信号处理模式,在用远低于奈奎斯特采样定理要求的速率采样时,它仍能实现准确的信号重构[11, 12]。结合压缩感知信号处理的特点,将压缩感知理论引入到目标跟踪的过程中,通过稀疏变换矩阵和观测矩阵的构造,实现回波信号的稀疏表示,并通过正交匹配追踪算法完成信号的高概率重构。使用压缩感知的前提条件是信号的稀疏表示,下面将分别介绍压缩感知理论和量测模型的稀疏表示。
3.1 压缩感知理论假设有一有限长的1维信号x,其在稀疏变换字典$\Psi =\{{{\psi }_{1}} {{\psi }_{2}} \cdots {{\psi }_{L}}\}$下的投影可以得到只有F个非零或者绝对值较大的系数,即$x=\Psi \Theta $,且$F\ll L$,则说明信号x在变换字典$\Psi $下是F稀疏的,且信号的稀疏度为F。
压缩感知理论指出,当信号x可以在稀疏变换字典$\Psi $上的投影具有稀疏的特性,就可以通过一个与$\Psi $不相关的$G\ll L$维观测矩阵对信号$\Upsilon (G\ll L)$进行非适应性线性量测,得到低维观测集合y,即
| ${{y}_{G\times 1}}={{\Upsilon }_{G\times L}}{{x}_{L\times 1}}={{\Upsilon }_{G\times L}}{{\Psi }_{L\times L'}}{{\Theta }_{L'\times 1}}$ | (10) |
信号的观测过程就是利用观测矩阵$\Upsilon $中的每个行向量分别对信号x进行投影,获取信号的部分信息,从而获得G个观测值。常用的观测矩阵包括随机高斯矩阵、伯努利矩阵、二值随机矩阵、局部傅里叶矩阵、部分单位矩阵和拓扑利兹矩阵等[8]。当观测维数满足$G\ge {{c}_{1}}F\cdot \lg \left( L/F \right)$时(其中c1为常数,本文取1),随机高斯矩阵$\Upsilon $与稀疏变换矩阵$\Psi $就能够以高概率从G个观测值中准确重构出原始信号。
3.2 基于压缩感知的量测模型通常,在第k时刻每一个目标的回波都可以由该时刻的时延和多普勒频移唯一确定,也就是说,回波信号是有M个子回波叠加:
| $r=\sum\limits_{m=0}^{M-1}{\overline{r}\left( \tau _{k}^{m},\nu _{k}^{m} \right)}$ | (11) |
| $\begin{align} & \bar{r}\left( \tau _{k}^{m},\nu _{k}^{m} \right) \\ & =\zeta _{k}^{m}\left[ \phi \left( 1,\tau _{k}^{m},\nu _{k}^{m} \right) \phi \left( 2,\tau _{k}^{m},\nu _{k}^{m} \right) \cdots \phi \left( N,\tau _{k}^{m},\nu _{k}^{m} \right) \right]_{N\times 1}^{\text{T}} \\ \end{align}$ |
| $r=\overline{\Phi }\varphi +w$ | (12) |
| $\overline{\Phi }={{\left[ \overline{r}\left( \tau _{k}^{1},\nu _{k}^{1} \right) \cdots \overline{r}\left( \tau _{k}^{i},\nu _{k}^{j} \right) \cdots \overline{r}\left( \tau _{k}^{{{N}_{\tau }}},\nu _{k}^{{{N}_{\nu }}} \right) \right]}_{N\times {{N}_{w}}}}$ |
| ${{\varphi }_{ij}}=\left\{ \begin{align} & 1\ , \left( \tau _{k}^{m},\nu _{k}^{m} \right)\text{=}\left( \tau _{k}^{i},\nu _{k}^{j} \right),\ \\ & \quad \ \ i=1,2,\cdots ,{{N}_{\tau }}; j=1,2,\cdots ,{{N}_{\nu }} \\ & 0, \ 其他\\ \end{align} \right.$ | (13) |
|
图 1 时延-多普勒域网格划分示例图 Fig.1 Example of delay-Doppler grid |
在第k时刻,假设雷达接收机收到3个目标的回波,那么,这3个回波可以由$\{(\tau _{k}^{m},\nu _{k}^{m}), m=1,2,3\}$唯一确定,$\{(\tau _{k}^{m},\nu _{k}^{m}), m=1,2,3\}$在时延-多普勒域对应的位置分别为A,B,C,坐标分别为(1,3),(12,10),(50,25),如图 2所示,则j可以表示为:
| $\begin{align} & \qquad \qquad \text{Index}=9\times {{N}_{\tau }}+12 \\ & \qquad \qquad \qquad \qquad \downarrow \\ & \varphi =[0,0,1,0,\cdots ,0,1,0,\cdots ,0,1,0,\cdots ,0]_{{{N}_{w}}\times 1}^{\text{T}} \\ & \qquad \qquad \uparrow \qquad \qquad \qquad \qquad \ \uparrow \\ & \qquad \ \text{Index}=3 \qquad \quad \text{Index}=24\times {{N}_{\tau }}+50 \\ \end{align}$ |
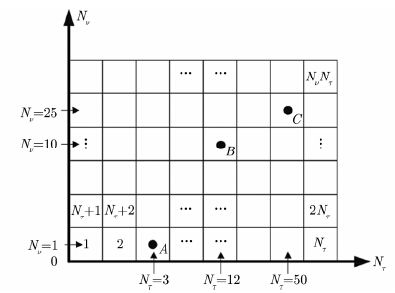
|
图 2 目标位置网格示意图 Fig.2 Sketch map of targets position in grid |
通过以上分析,j中只有少数(目标的数目M) 元素为1,绝大多数(Nw-M)元素都为0,且满足($M\ll {{N}_{w}}-M$),以上过程即完成了回波信号的稀疏表示,且稀疏度为M。
显然,$\overline{\Phi }$即为稀疏变换矩阵,进一步,选择随机高斯矩阵作为观测矩阵,对回波信号进行降维观测,本文采用正交匹配追踪重构算法,正交匹配追踪算法在匹配追踪算法的基础上,通过对已选择的原子集进行施密特正交化处理,保证每次迭代后信号的残余分量与之前选择的匹配原子正交[11],使得算法的收敛速度加快。
以上时延多普勒网格分析方法,重构结果即可得到回波信号的时延和多普勒频移,而不需要再用模糊函数或者匹配滤波等方式对回波信号再做处理,在一定程度上减少了计算量,同时减少了旁瓣误差,提高了测量精度。
4 目标跟踪算法本文量测方程式(6)中的矩阵Φ是目标运动状态${{\xi }_{k}}$的非线性函数矩阵,即$\Phi \text{=}f\left( \xi _{k}^{m} \right)$,使得无迹卡尔曼滤波或者容积卡尔曼滤波不能很好地跟踪上目标,因此这里采用粒子滤波实现目标跟踪。另外,考虑到提高计算效率,解决粒子贫乏问题,增强目标的跟踪性能等因素,因此,本文采用粒子群优化粒子滤波实现目标的跟踪。
粒子群优化滤波方法的基本原理是:将最新观测值融合到采样过程中,并对采样过程利用粒子群优化算法进行优化,使粒子集朝着高似然区运动[13, 14]。
具体跟踪算法如下:
(1) 首先将最新的量测值引入到采样过程,并定义适应度函数:
| $\text{Fn}=\exp \left[ -{{{\left( {{r}_{k}}-\widehat{r}_{k|k-1}^{i} \right)}^{2}}}/{2{{R}_{k}}}\; \right]$ | (14) |
(2) 初始化。初始时刻,从重要性函数采样Np个粒子$\{\xi _{0:k}^{i},1/N\}_{i=1}^{N}$作为样本。
(3) 更新过程:
第i个粒子从初始状态到当前迭代次数搜索最优值为个体极值Pp,种群从初始状态到当前迭代次数搜索最优值为全局极值Pg,根据最优值通过式(15),式(16)更新每个粒子的速度和位置。
| $\begin{align} & \qquad \qquad \ {{\left( \mu _{k}^{m} \right)}^{\left( i \right)}}=\left| \text{randn(}n\text{)} \right|\left( {{P}_{\text{p}}}-{{\left( \xi _{k}^{m} \right)}^{\left( i \right)}} \right) \\ & \qquad \qquad \ \qquad \qquad +\left| \text{Randn(}n\text{)} \right|\left( {{P}_{\text{g}}}-{{\left( \xi _{k}^{m} \right)}^{\left( i \right)}} \right) \\ \end{align}$ | (15) |
| ${{\left( \xi _{k+1}^{m} \right)}^{\left( i \right)}} \! \! ={{\left( \xi _{k}^{m} \right)}^{\left( i \right)}}+{{\left( \mu _{k}^{m} \right)}^{\left( i \right)}}$ | (16) |
(4) 计算重要性权值:
| ${{\left( \omega _{k}^{m} \right)}^{\left( i \right)}}={{\left( \omega _{k-1}^{m} \right)}^{\left( i \right)}}\exp \left[ -{{{\left( {{r}_{k}}-\widehat{r}_{k|k-1}^{i} \right)}^{2}}}/{2{{R}_{k}}}\; \right]$ | (17) |
对权值归一化处理得到
| ${{\left( \omega _{k}^{m} \right)}^{\left( i \right)}}={{{\left( \omega _{k}^{m} \right)}^{\left( i \right)}}}/{\sum\limits_{i=1}^{{{N}_{\text{p}}}}{{{\left( \omega _{k}^{m} \right)}^{\left( i \right)}}}}\;$ | (18) |
(5) 重采样:为了解决粒子退化问题,选择和复制较大权值的粒子,将带有权值的样本映射为等权值样本。
| $\left\{ {{\left( \xi _{0:k}^{m} \right)}^{\left( i \right)}},{1}/{{{N}_{\text{p}}}}\; \right\}_{i=1}^{{{N}_{\text{p}}}}=\left\{ {{\left( \xi _{0:k}^{m} \right)}^{\left( i \right)}},{{\left( \omega _{k}^{m} \right)}^{\left( i \right)}} \right\}_{i=1}^{{{N}_{\text{p}}}}$ | (19) |
(6) 输出:
状态估计:$\widehat{\xi }_{k}^{m}=\sum\limits_{i=1}^{{{N}_{\text{p}}}}{{{\left( \omega _{k}^{m} \right)}^{\left( i \right)}}{{\left( \xi _{k}^{m} \right)}^{\left( i \right)}}}$
方差估计:
| ${{\widehat{p}}_{k}}=\sum\limits_{i=1}^{N}{{{\left( \omega _{k}^{m} \right)}^{\left( i \right)}}\left( {{\left( \xi _{k}^{m} \right)}^{\left( i \right)}}-{{\left( \widehat{\xi }_{k}^{m} \right)}^{\left( i \right)}} \right)}{{\left( {{\left( \xi _{k}^{m} \right)}^{\left( i \right)}}-{{\left( \widehat{\xi }_{k}^{m} \right)}^{\left( i \right)}} \right)}^{\text{T}}}$ |
由第(6)步可知目标在第k时刻的状态为:
| $\widehat{\xi }_{k}^{m}=\sum\limits_{i=1}^{{{N}_{p}}}{{{\left( \omega _{k}^{m} \right)}^{\left( i \right)}}{{\left( \xi _{k}^{m} \right)}^{\left( i \right)}}}$ |
在利用认知雷达跟踪目标时,常用波形设计准则有最大信噪比准则、互信息准则、PCRB准则等,输出信噪比是反映雷达性能的一个重要参数,雷达的跟踪性能和信噪比有着密切联系,但是点目标高斯白噪声情况下的输出信噪比与发射波形无关,互信息准则必须满足目标冲激响应已知的条件,而PCRB准则具有适用范围广,设计精度高的特点,不受以上制约的影响。综合考虑,本文选择了基于PCRB的波形参数设计方法,认知雷达波形参数设计流程如图 3所示,发射信号波形与跟踪结果形成了闭环反馈。
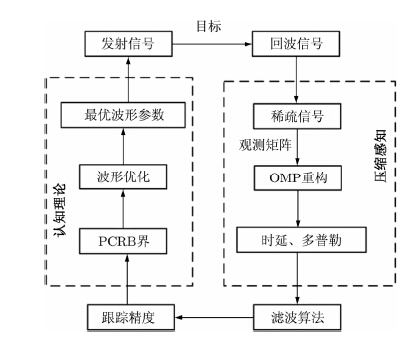
|
图 3 认知波形参数设计处理流程图 Fig.3 Cognitive waveform parameter design |
关于目标运动状态向量$\xi _{k}^{m}$的PCRB可以表示为[15]:
| $E\left[ \left( \xi _{k}^{m}-\widehat{\xi }_{k}^{m} \right){{\left( \xi _{k}^{m}-\widehat{\xi }_{k}^{m} \right)}^{\text{T}}} \right]\ge {{J}^{-1}}$ | (20) |
| ${{J}_{k}}\triangleq -\text{E}\left[ \Delta _{{{\Xi }_{k}}}^{{{\Xi }_{k}}}\lg p\left( {{r}_{1:k}},\xi _{0:k}^{m} \right) \right]$ | (21) |
| $\begin{align} & {{J}_{k+1}}\left( {{\theta }_{k+1}} \right)={{\Omega }_{k}}-{{\left( D_{k}^{12} \right)}^{\text{T}}}{{\left( {{J}_{k}}\left( {{\theta }_{k}} \right)+D_{k}^{11} \right)}^{-1}}D_{k}^{12} \\ & \qquad \qquad \qquad +{{\Gamma }_{k+1}}\left( {{\theta }_{k+1}} \right) \\ \end{align}$ | (22) |
| ${{\Gamma }_{k+1}}\left( {{\theta }_{k+1}} \right)=-{{E}_{{{r}_{k+1}}, \ \ {{\xi }_{k+1}}}} \ \ \left[ \Delta _{{{\Xi }_{k}}}^{{{\Xi }_{k}}}\lg p\left( {{r}_{k+1}}\left( {{\theta }_{k+1}} \right)|\xi _{k+1}^{m} \right) \right]$ |
| ${{\widetilde{\Gamma }}_{k+1}}\left( {{\theta }_{k+1}} \right)=-{{E}_{{{r}_{k+1}}, \ \ \xi _{k+1}^{m} \ \ \ |{{r}_{1:k}}}}\left[ \Delta _{{{\Xi }_{k+1}}}^{{{\Xi }_{k+1}}}\lg p\left( {{r}_{k+1}}\left( {{\theta }_{k+1}} \right) \ \ |\xi _{k+1}^{m} \right) \right]$ | (23) |
于是最优波形发射参数为:
| $\theta _{k + 1}^* = \arg \;\mathop {\max }\limits_{\mathop {{\theta _{k + 1}}\; \in \Theta \;}\limits_{} } {\mkern 1mu} \;\;{\rm{Tr}}\left\{ {{{\tilde \Gamma }_{k + 1}}\left( {{\theta _{k + 1}}} \right)} \right\}$ | (24) |
| ${{\widetilde{\Gamma }}_{k+1}}\left( {{\theta }_{k+1}} \right)\approx \frac{1}{{{N}_{r}}}\sum\limits_{i=1}^{{{N}_{s}}}{\sum\limits_{j=1}^{{{N}_{r}}}{\varpi _{k}^{(i)}}}\Lambda \left( r_{k+1}^{(j)}\left( {{\theta }_{k+1}} \right),{{\left( \xi _{k+1}^{m} \right)}^{\left( i \right)}} \right)$ | (25) |
于是基于PCRB的波形参数为:
| $\begin{align} & \theta _{k+1}^{*}({{\lambda }_{k+1}},{{b}_{k+1}}) \\ & =\arg \ \underset{{{\theta }_{k+1}}\in \Theta }{\mathop{\max }}\, \text{Tr}\left\{ \frac{1}{{{N}_{r}}}\sum\limits_{i=1}^{{{N}_{s}}}{\sum\limits_{j=1}^{{{N}_{r}}}{\varpi _{k}^{(i)}}}\Lambda \left( r_{k+1}^{(j)}\left( {{\theta }_{k+1}} \right),{{\left( \xi _{k+1}^{m} \right)}^{\left( i \right)}} \right) \right\} \\ \end{align}$ | (26) |
由此完成对认知跟踪雷达发射波形的设计。考虑到波形参数设计中仅对l和b进行了改变,因此设计后的发射波形仍然满足广义调频信号的条件。
6 仿真与分析在本节中对本文方法进行仿真,仿真环境设置如下:
雷达的位置$(x_{k}^{0},y_{k}^{0})=$(0 m,0 m),目标个数为3,${{\theta }_{0}}={{\left[ {{\lambda }_{0}} {{b}_{0}} \right]}^{\text{T}}}={{\left[ 1 \mu \text{s},5\times {{10}^{8}} {{\text{s}}^{-2}} \right]}^{\text{T}}},$△Τ=3.33 ns,△β=2.46e-9,网格数目设置为:a0=400和b0=40,数据模拟所需参数设定见表 1。
| 表 1 仿真参数设置 Tab. 1 Values of parameters for simulation |
在这里,仿真考虑了目标轨迹交叉和不交叉两种情况,如表 2所示。两种状态下各个目标的初始状态分别为:
| 表 2 目标初始状态设置 Tab. 2 Values of initials statement for simulation |
仿真1 为了分析降采样条件下目标的跟踪性能,基于量测方程式(6),构建稀疏变换矩阵,观测矩阵采用高斯随机矩阵,分析了两种运动轨迹情况下的跟踪情况。
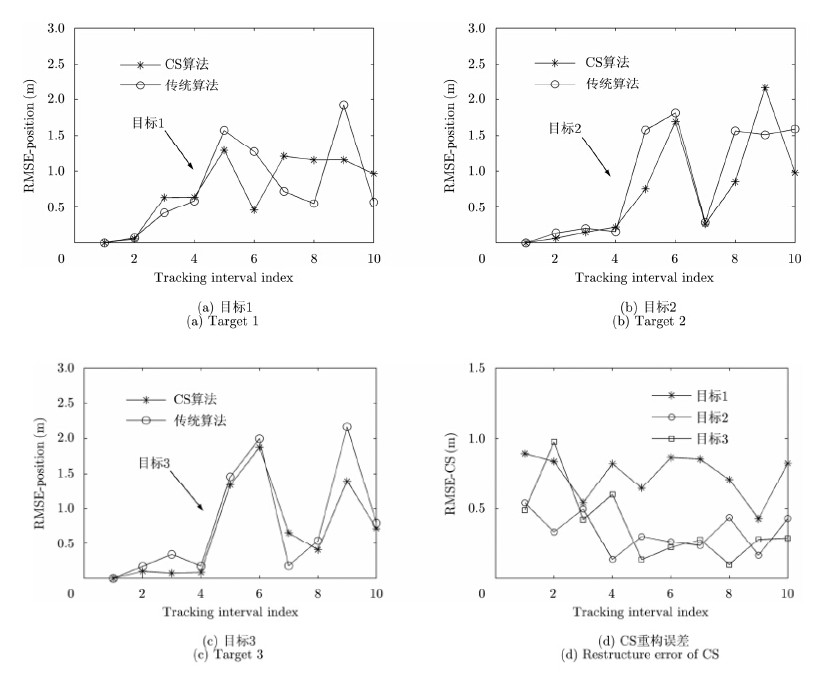
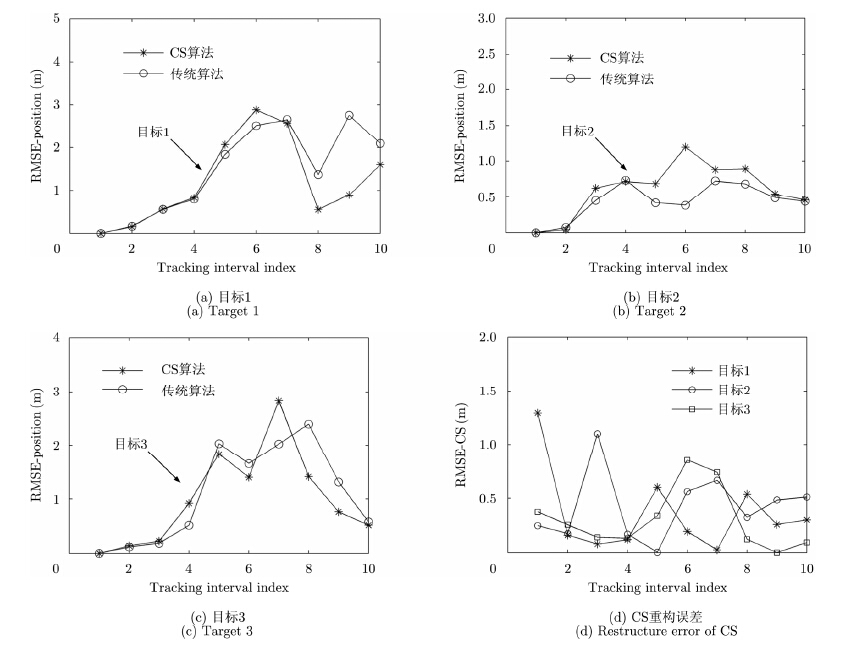
图 4,图 5和图 6分别示出了轨迹交叉和不交叉两种条件下目标的位置估计情况以及相应的均方根误差与迭代次数的关系,由图 4(a),图 4(b)可知,在目标交叉和不交叉两种情况下,基于压缩感知的降采样条件下的目标跟踪方法都能够较好地跟踪上目标,较传统的采样方式,能够提供几乎相当的跟踪效果。进一步分析各个目标的跟踪RMSE如图 5,图 6所示,图 5(a),图 6(a)为压缩感知重构的误差随迭代次数变化情况,从图中可以看出,多个目标能够通过OMP算法很好地重构出来,并且误差在0.033%之内,从而验证了稀疏量测模型建立的可靠性。图 5(b),图 5(c),图 5(d)分别为目标1,目标2,目标3的跟踪均方根误差,从图中可以看出,基于压缩感知的降采样条件下的跟踪均方根误差与传统算法具有几乎一致的变化规律,在数值上也是非常接近的,进而验证了所提方法能够很好地满足目标跟踪的要求。比较图 5和图 6可以看出,交叉情况下的跟踪精度要略低于不交叉的情况,那是因为仿真中交叉情况下同一时刻3个目标的时延和多普勒所处区域较小,甚至处于同一网格中,造成稀疏采样信号在重构的过程中误差增大,进而导致算法跟踪精度降低;在轨迹不交叉运动模型中,多目标在网格中的位置相对稳定,不存在相距过近的情况,因此其跟踪精度高于轨迹交叉模型。在数据量方面,按照奈奎斯特采样定理的要求,传统采样算法至少需要2000个采样点,而本文算法中,为了高概率地重构出量测信息,我们随机抽取了300个采样点即完成了目标的跟踪。
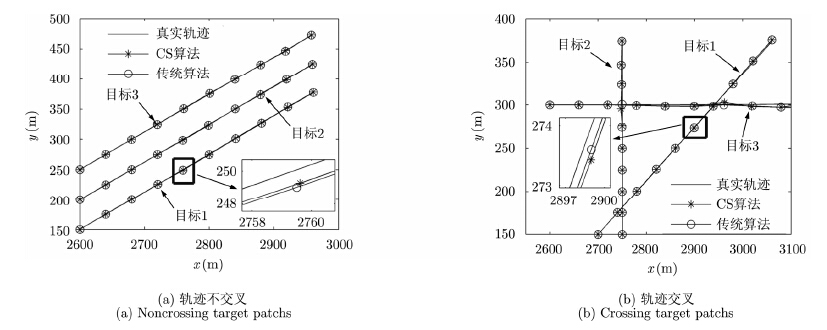
|
图 4 目标位置变化随迭代次数变化情况 Fig.4 Target position versus tracking interval index |
|
图 5 不交叉条件下目标跟踪RMSE与迭代次数关系 Fig.5 Relation between RMSE and tracking interval index for non-crossing target paths |
|
图 6 交叉条件下目标跟踪RMSE与迭代次数关系 Fig.6 Relation between RMSE and tracking interval index for crossing target paths |
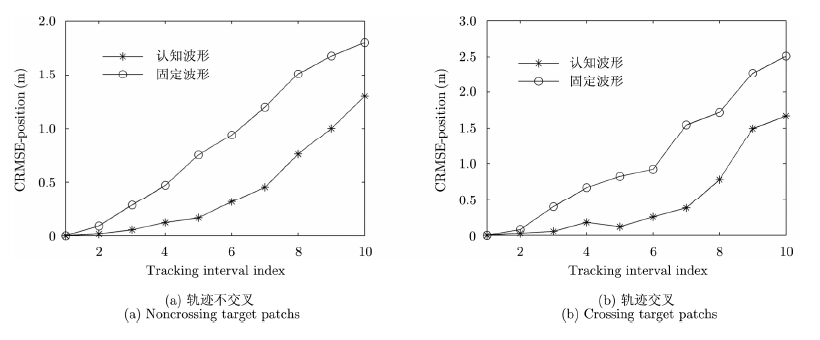
仿真2 在本节中,进一步比较了本文所提基于PCRB的认知雷达波形参数设计与传统固定波形参数设计雷达跟踪性能,此处进行了Nm=100次蒙特卡罗仿真,目标位置的估计的联合均方根误差(Composite Root Mean Squared Error,CRMSE),定义如下:
| $\text{CRMS}{{\text{E}}_{r}}=\frac{1}{M{{N}_{m}}}\sum\limits_{i=1}^{{{N}_{m}}}{\sum\limits_{m=1}^{M}{\sqrt{{{\left( {{x}_{m}}-{{\widehat{x}}_{m,i}} \right)}^{2}}+{{\left( {{y}_{m}}-{{\widehat{y}}_{m,i}} \right)}^{2}}}}}$ | (27) |
|
图 7 固定波形和认知波形目标跟踪的RMSE随迭代次数变化情况 Fig.7 Comparison of tracking result for fixed and cognitive waveform radar |
从图 7中可以看出,在两种目标的运动情况下,基于PCRB的认知雷达波形参数设计的跟踪方法,目标跟踪性能均优于传统固定波形参数设计跟踪方法,都能够很好地改善目标的跟踪性能。另外,轨迹不交叉和交叉两种情况下,认知波形参数设计较传统固定波形参数设计的跟踪性能分别提高了62.45%和57.58%,这表明轨迹交叉降低了认知波形参数设计对跟踪性能的改善效果。
综上所述,基于压缩感知的认知雷达波形参数设计方法能够有效提高目标跟踪性能,降低雷达信号处理数据量。仿真结果验证了该算法的有效性。
7 结论本文提出了基于压缩感知的多目标认知雷达跟踪方法。通过构建时延和多普勒网格,实现了目标回波信号的稀疏表示,并通过正交匹配追踪算法完成对稀疏信号进行重构。在此基础上,考虑到传统的粒子滤波容易陷入局部最优,对粒子数目要求大等问题,采用了粒子群优化的粒子滤波来对目标状态进行实时估计。然后将认知雷达波形参数设计思想引入到基于压缩感知的目标跟踪中,通过优化跟踪精度PCRB认知的设计雷达发射波形参数。最后以2维空间中匀速运动交叉和不交叉运动模型进行实验仿真。仿真表明,相比于传统跟踪方法,本文所提跟踪方法不仅有效地减少了雷达的数据量,而且较大地提高了目标的跟踪性能。
| [1] | 黎湘, 范梅梅. 认知雷达及其关键技术研究进展[J]. 电子学报, 2012, 40(9): 1863-1870. Li Xiang and Fan Mei-mei. Research advance on cognitive radar and its key technology[J]. Acta Electronica Sinica, 2012, 40(9): 1863-1870.(  1) 1) |
| [2] | Haykin S. Cognitive radar: a way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30-40.( 1) 1) |
| [3] | Haykin S, Zia A, Arasaratnam I, et al.. Cognitive tracking radar[C]. Proceedings of 2010 IEEE Radar Conference, Washington DC, 2010: 1467-1470.( 2) 2) |
| [4] | Chavali P and Nehorai A. Cognitive radar for target tracking in multipath scenarios[C]. Proceedings of 2010 IEEE Waveform Diversity and Design Conference, Niagara Falls, Canada, 2010: 110-114.( 1) 1) |
| [5] | Chavali P and Nehorai A. Scheduling and power allocation in a cognitive radar network for multiple-target tracking[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 715-729.( 1) 1) |
| [6] | Canaes E and Tao T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203-4215.( 1) 1) |
| [7] | Canaes E, Romberg J, and Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223.( 1) 1) |
| [8] | Canaes E. Compressive sampling[C]. Proceedings of the International Conference of Mathematicians, Madrid, Spain, 2006: 1433-l452.( 2) 2) |
| [9] | SIRA S P. Time-varying waveform selection and configuration for agile sensors in tracking applications[C]. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, Pennsylvania, 2005: 880-884.( 1) 1) |
| [10] | 薛文虎, 张社国, 徐红华. 用于目标跟踪的自适应广义调频波形设计算法[J]. 海军工程大学学报, 2012, 24(4): 67-71. Xue Wen-hu, Zhang She-guo, and Xu Hong-hua. An adaptive waveform design algorithm for target tracking based on generalized frequency modulation[J]. Journal of Naval University of Engineering, 2012, 24(4): 67-71.(  1) 1) |
| [11] | 石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081. Shi Guang-ming, Liu Dan-hua, Gao Da-hua, et al.. Advances in theory and application of compressed sensing[J]. Acta Electronica Sinica, 2009, 37(5): 1070-1081.(  2) 2) |
| [12] | 时燕, 陈迪荣. 基于小波包算法的压缩传感SAR 成像方法[J]. 雷达学报, 2013, 2(2): 218-225. Shi Yan and Chen Di-rong. A compressive sensing SAR imaging approach based on wavelet package algorithm[J]. Journal of Radars, 2013, 2(2): 218-225.(  1) 1) |
| [13] | 方正, 佟国峰, 徐心和. 粒子群优化粒子滤波方法[J]. 控制与决策, 2007, 22(3): 273-277. Fang Zheng, Tong Guo-feng, and Xu Xin-he. Particle swarm optimized particle filter[J]. Control and Decision, 2007, 22(3): 273-277.(  1) 1) |
| [14] | 朱志宇. 粒子滤波算法及其应用[M]. 北京: 科学出版社, 2010: 80-81. Zhu Zhi-yu. Particle Filter Algorithm and Its Application[M]. Beijing: Science Press, 2010: 80-81.(  1) 1) |
| [15] | Kershaw D and Evans R. Optimal waveform selection for tracking systems[J]. IEEE Transactions on Information Theory, 1994, 40(9): 1536-1550.( 1) 1) |
| [16] | Tichavský P, Muravchik C H, and Nehorai A. Posterior Cramér-Rao bounds for discrete-time nonlinear filtering[J]. IEEE Transactions on Signal Processing, 1998, 46(5): 1386-1394.( 3) 3) |


