②(华中科技大学电子与信息工程系 武汉 430074)
②(Huazhong University of Science and Technology, Wuhan430074, China)
带通欠采样是对脉冲超宽带(Pulse Position Modulation-Ultra Wide Band,PPM-UWB)信号的低于奈奎斯特采样率的采样方法,对PPM-UWB数字接收机的研究具有重要的实用价值[1]。PPM-UWB数字接收机的应用主要有室内高速通信、测距与定位、遥感以及汽车雷达等[2, 3, 4]。PPM信号是一类脉冲宽度特别窄,占空比非常小的信号。近几年来,对PPM-UWB的带通欠采样信号处理的研究正在逐步深入。首先,新息率概念的提出,即单位时间内信号的特征数,通常这个数值与信号速率相关,使得非带限脉冲信号的欠采样成为可能[5];其次,按照新息率进行采样和重建的零化滤波算法可以在没有噪声的情况下准确重建原始非带限脉冲信号[6];然后,在提高采样率的情况下的零化滤波算法具有一定程度上的抗噪声性能[7, 8, 9],使用总体最小二乘(Total Least Squares,TLS)解调方法比最小二乘(Least Squares,LS)解调方法具有更好的抗噪声性能[10];最近,采用旋转不变性技术而进行的信号参数估计(Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT)算法,能够在低信噪比的条件下重建算法的性能[11, 12, 13]。零化滤波算法和ESPRIT算法在PPM-UWB的信号重建方面的研究主要集中于采样率对性能的影响,本文提出在满足最低要求的信号新息率采样的条件下,增大采样率并不能提高系统的性能,影响其性能的因素是带通滤波器的带宽。本文探讨了PPM-UWB信号的重建算法,对ESPRIT算法进行了TLS解的补充,并且对零化滤波算法和ESPRIT算法进行了性能分析。
本文首先在PPM-UWB信号处理中分析了零化滤波算法的可行性,并引入了LS和TLS解,然后分析了ESPRIT算法的可行性,同时也引入了LS解和TLS解,最后以仿真的形式对ESPRIT算法与零化滤波算法进行了性能对比。
2 零化滤波算法冲激串信号$x\left( t \right) = \sum\nolimits_{i = 1}^p {{d_i}\delta \left( {t - {t_i}} \right)} $的傅里叶变换为 $X\left( f \right) = \sum\nolimits_{i = 1}^p {{d_i}{{\rm{e}}^{ - {\rm{j}}2{π} f{t_i}}}} $,在整数倍频率间隔 kf0 上
| $\begin{aligned} X\left[k \right] & = X\left( {k\mathit{f}_{\rm{0}}} \right)\\ & = \sum\limits_{i = 1}^p {{d_i}{{\rm{e}}^{ - {\rm{j}}2{π}k\mathit{f}_{\rm{0}}{t_i}}}} = \sum\limits_{i = 1}^p {{d_i}{{\left( {{{\rm{e}}^{ - {\rm{j}}2{π}\mathit{f}_{\rm{0}}{t_i}}}} \right)}^k}} \end{aligned}$ | (1) |
冲激串信号x(t)的傅里叶变换X[k]为p个信号${{\rm{e}}^{ - {\rm{j}}2{π}\mathit{f}_{\rm{0}}{t_i}}}$(i=1,2,···,p)的指数和,令${u_i} = {{\rm{e}}^{ - {\rm{j}}2{π}\mathit{f}_{\rm{0}}{t_i}}}$,i=1,2,···,p,则$X\left[k \right] = \sum\nolimits_{i = 1}^p {{d_i}{{\left( {{u_i}} \right)}^k}} $。其中f0是信号的频率分辨率,即频域信号的最小频率间隔,此间隔只与所取的信号长度有关,与采样率无关。
为了从冲激串频域信号X[k]中估计其幅度di和时移ti,定义
| $\begin{aligned} X\left[k \right] & = X\left( {k\mathit{f}_{\rm{0}}} \right)\\ & = \sum\limits_{i = 1}^p {{d_i}{{\rm{e}}^{ - {\rm{j}}2{π}k\mathit{f}_{\rm{0}}{t_i}}}} = \sum\limits_{i = 1}^p {{d_i}{{\left( {{{\rm{e}}^{ - {\rm{j}}2{π}\mathit{f}_{\rm{0}}{t_i}}}} \right)}^k}} \end{aligned}$ | (2) |
使得$\left( {a * X} \right)\left[k \right] = \sum\nolimits_{m = 0}^p $a[m]X[k-m]=0,a[0]=1,称j(z)为信号x(t)的零化滤波器。如果求解出了j(z)的系数a,那么零点μi就可以通过a求得,时移ti就能通过ui求解出来。当求解出时移ti后,幅度di可以通过时移ti和X[k]求得。
由于当带通滤波器的带宽刚好等于信号新息率时,容易受到噪声的影响[3],本文都是讨论带通滤波器带宽大于信号新息率时的情形。将冲激串频域信号X[k]代入零化滤波器中,得到一组超定方程组Pa=-Q(当带通滤波器的带宽刚好等于信号新息率时,得到的是正定方程组),其中P是由X[k]组成的一个行数大于列数的矩阵,a是由零化滤波器系数组成的向量,Q是由X[k]组成的向量。求解这个超定方程组有两种不同的方法:LS和TLS。
(1) LS解法
此时方程组中的矩阵P为J×p维,为了更好地区分两种求解超定方程组的方法,LS解法中方程组中的P和Q都用下标1进行标注(TLS解法中用下标2进行标注),在LS解法中,通过对矩阵${{P}_1}$进行奇异值分解,来求解零化滤波器的系数a。
| ${{P} _1} = \left[{\begin{array}{c} {X\left[L \right]} & {X\left[{L - 1} \right]} & \cdots & {X\left[{L + p - 1} \right]}\\ {X\left[{L + 1} \right]} & {X\left[L \right]} & \cdots & {X\left[{L + p - 2} \right]}\\ \vdots & \vdots & \ddots & \vdots \\ {X\left[{L + J - 1} \right]} & {X\left[{L + J - 2} \right]} & \cdots & {X\left[{L + J - p} \right]} \end{array}} \right] \hspace{40pt}$ |
| ${{a}} = {\left[ {a\left[1 \right]} {a\left[2 \right]} \cdots {a\left[p \right]} \right]^{\rm{T}}} ,\quad {{Q}_1} = \left[{X\left[{L + 1} \right]X\left[{L + 2} \right] \cdots } \right.{\left. {X\left[{L + J} \right]} \right]^{\rm{T}}}$ |
P1的奇异值分解为P1=U1S1V1H,系数的解为a=-V1S1U1HQ1。
(2) TLS解法
若将方程组中的信号采样矩阵进行如下处理,此时方程组中的P2矩阵为G×p维:其中G为矩阵P2的行数,G>p:
| ${{P}_2} = \left[{\begin{array}{*{20}{c}} {X\left[L \right]} & {X\left[{L - 1} \right]} & \cdots & {X\left[{L + p - 1} \right]}\\ {X\left[{L + 1} \right]} & {X\left[L \right]} & \cdots & {X\left[{L + p - 2} \right]}\\ \vdots & \vdots & \ddots & \vdots \\ {X\left[{L + {Γ} - 1} \right]} & {X\left[{L + {Γ} - 2} \right]} & \cdots & {X\left[{L + {Γ} - p} \right]} \end{array}} \right] \hspace{40pt}$ |
| ${{a}} = {\left[ {a\left[1 \right]} {a\left[2 \right]} \cdots {a\left[p \right]} \right]^{\rm{T}}} ,\quad {{Q}_1} = \left[{X\left[{L + 1} \right]X\left[{L + 2} \right] \cdots } \right.{\left. {X\left[{L + Γ} \right]} \right]^{\rm{T}}}$ |
构造增广矩阵C: C=[P2|Q2]$ \in $CG×(p+1)将C进行奇异值分解为C=U2S2V2H,其中
| ${{U}_2} = \left[ {{u_1}} {{u_2}} \cdots {{u_{Γ} }} \right] \hspace{32pt}$ |
| ${{\bf{{Σ} }}_2} = {\rm{diag}}\left( {{\sigma _1}} {{\sigma _2}} \cdots {{\sigma _{p + 1}}} \right)$ |
| ${{V}_2} = \left[ {{v_1}} {{v_2}} \cdots {{v_{p + 1}}} \right] \hspace{29pt}$ |
式中S2是由矩阵奇异值构成的G×(p+1)维矩阵,且对角线上的元素按照降序排列:
| ${\sigma _1} \ge {\sigma _2} \ge \cdots \ge {\sigma _p} > {\sigma _{p + 1}}$ |
则方程组的TLS解为:
| ${a} = \frac{{{{\left[{ {{v_{p + 1}}\left( 1 \right)} {{v_{p + 1}}\left( 2 \right)} \cdots {{v_{p + 1}}\left( p \right)} } \right]}^{\rm{T}}}}}{{{v_{p + 1}}\left( {p + 1} \right)}}$ | (3) |
当使用上述的任意一种方法求解出零化滤波器系数a后,将零化滤波器j(z)作因式分解,求解滤波器的零点ui,通过${u_i} = {{\rm{e}}^{ - {\rm{j}}2{π} \mathit{f}_{\rm{0}}{t_i}}}$,i=1,2,···,p即可求出时移ti,再由$X\left[k \right] = \sum\nolimits_{i = 1}^p {{d_i}{{\left( {{u_i}} \right)}^k}} $即可计算出信号的幅度di。
零化滤波算法在计算过程中要经过矩阵的奇异值分解和多项式求根,在LS求解的过程中经过了3次矩阵乘法和1次矩阵求逆运算,在TLS求解过程中,仅经过了1次排序和向量乘法运算。在计算复杂度上,TLS要比LS简单。
3 ESPRIT算法
考虑一个单一的复指数
| $s\left[{k + 1} \right] = d{{\rm{e}}^{ - {\rm{j}}2{π} \mathit{f}_{\rm{0}}t\left( {k + 1} \right)}} = s\left[k \right]{{\rm{e}}^{ - {\rm{j}}2{π} \mathit{f}_{\rm{0}}t}}$ | (4) |
也就是下一个频率采样值是当前频率采样值的相移的结果。这个相移可以表示为:在单位圆上的一个${{\rm{e}}^{ - {\rm{j}}2{π} \mathit{f}_{\rm{0}}t}}$的转动。由冲激串频域信号X[k]组成的矢量信号X[k]可以分解为由时移频率响应成分S[k]和噪声成分w[k]组成的频率窗口矢量模型:
| $\begin{aligned} {X}\left[k \right] & = \sum\limits_{i = 1}^p {{d_i}s\left( {{t_i}} \right){{\rm{e}}^{ - {\rm{j}}2{π} k\mathit{f}_{\rm{0}}{t_i}}}} + {w}\left[k \right]\\ & = {S}{{j} ^k}{d} + {w}\left[k \right]\\ & = {s}\left[k \right] + {w}\left[k \right] \end{aligned}$ | (5) |
这里,矩阵S的p个列:S=[s(t1) s(t2) ··· s(tp)]是长为M的频率窗口时间复指数矢量。矢量d由复指数的幅度di组成。另一方面,矩阵j是表示S[k]的单独复指数分量的相邻频率采样值之间相位移动的对角矩阵:
| $\begin{aligned} {j} & = {\rm{diag}}\left\{ {{u_1},{u_2},\cdots ,{u_p}} \right\}\\ {\rm{ }} & = \left[{\begin{array}{*{20}{c}} {{{\rm{e}}^{ - {\rm{j}}2{π} \mathit{f}_{\rm{0}}{t_1}}}}& 0& \cdots & 0\\ 0& {{{\rm{e}}^{ - {\rm{j}}2{π} \mathit{f}_{\rm{0}}{t_2}}}}& \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0& \cdots & 0& {{{\rm{e}}^{ - {\rm{j}}2{π} \mathit{f}_{\rm{0}}{t_p}}}} \end{array}} \right] \end{aligned}$ | (6) |
这里,${u_i} = {{\rm{e}}^{ - {\rm{j}}2{π} \mathit{f}_{\rm{0}}{t_i}}},i = 1,2,\cdots ,p$。由于复指数的时间完全描述了这个旋转矩阵,时间估计可以通过求出j而得到。ESPRIT要解决的就是在仅已知冲激串频域信号X[k]的情况下对矩阵j进行求解。
ESPRIT的实质在于其在交错的子空间之间的转动特性,这些子空间被调用以得到式(1)中时移ti的估计。在离散频域信号的情况下,这个特性依赖于在两个频率上交错的相同区间上的信号观测值[14]。
首先对未知的时移频率响应矩阵S进行分析,考虑在长为M的频率窗矢量中,两个交叠的、长为M-1的子窗口。这个子窗口的运算如图 1所示。
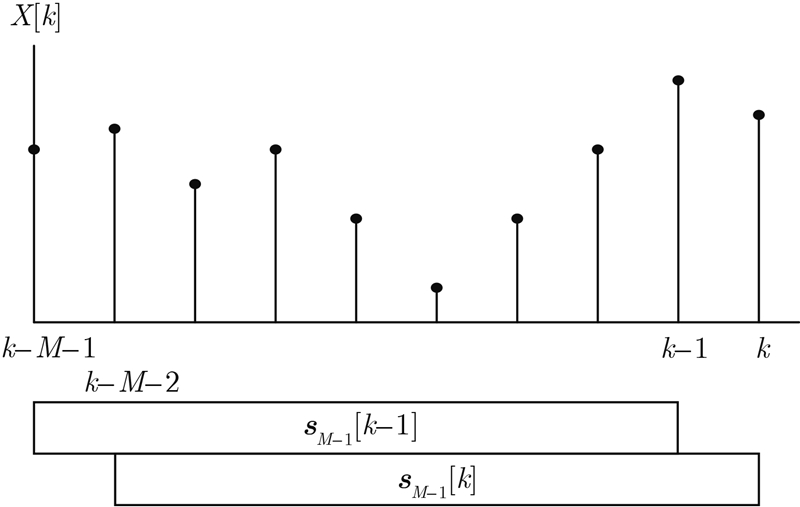 | 图 1 ESPRIT算法采用的频率交错、重叠窗Fig.1 Interleaving and overlap window used for ESPRIT algorithm |
考虑由复指数的和组成的信号:
| ${s}\left[k \right] = \left[{\begin{array}{*{20}{c}} {{{s}_{M - 1}}\left[k \right]}\\ {s\left[{k + M - 1} \right]} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {s\left[k \right]}\\ {{{s}_{M - 1}}\left[{k + 1} \right]} \end{array}} \right]$ | (7) |
这里,sM-1[k]是s[k]的长为M-1的子窗口,即:
sM-1 [k]=SM-1jnd
除了它的频率窗口时间矢量的长度是M-1外,矩阵SM-1和S以相同的方式构造,记为sM-1(t):
SM-1 =[sM-1(t1) sM-1(t2) ··· sM-1(tp)]
s[k]是在频率kf0由复指数的和构成的标量信号。定义矩阵:
| ${{S}_1} = {{S}_{M - 1}}{{j} ^n},\quad {{S}_2} = {{S}_{M - 1}}{{j} ^{n + 1}}$ | (8) |
这里,S1和S2对应非交错的和交错的窗口,即:
| ${S} = \left[{\begin{array}{*{20}{c}} {{{S}_1}}\\ { * * \cdots * } \end{array}} \right] = \left[{\begin{array}{*{20}{c}} { * * \cdots * }\\ {{{S}_2}} \end{array}} \right]$ | (9) |
这两个窗口频率矢量的矩阵有如下关系:S2=S1j,两个矩阵各自生成一个虽然不同、但相互联系的M-1维子空间。
图 2是描述ESPRIT算法进行PPM-UWB信号时移估计的流程方框图。
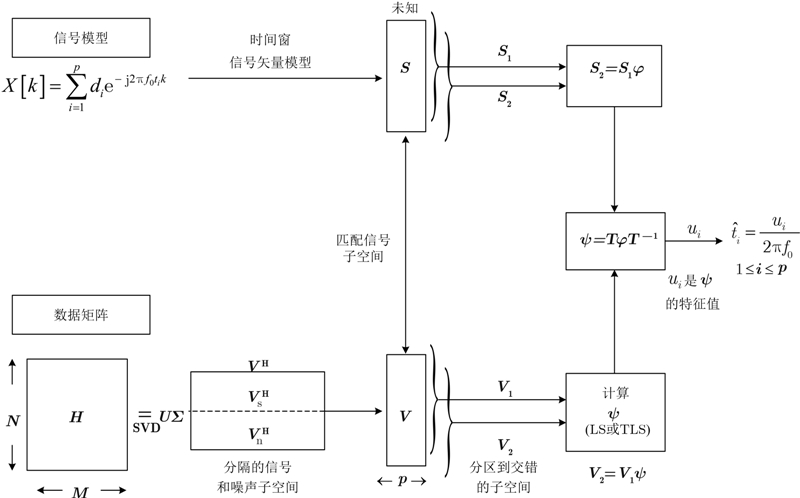 | 图 2 由数据矩阵开始经时移估计的ESPRIT算法流程方框图Fig. 2 The block diagram of ESPRIT algorithm process (Time shift estimate from data matrix) |
ESPRIT算法的计算流程如下:
(1) 由冲激串频域信号X[k],构造一个Hankel矩阵:
| ${H} = \left[{\begin{array}{*{20}{c}} {X\left[{L - \lambda } \right]} & \quad \,{X\left[{L - \lambda + 1} \right]} \quad & \quad \cdots \quad & {X\left[{L - \lambda + M - 1} \right]}\\ {X\left[{L - \lambda + 1} \right]} & \quad \,{X\left[{L - \lambda + 2} \right]} \quad & \quad \cdots \quad & {X\left[{L - \lambda + M} \right]}\\ \vdots & \vdots & \ddots & \vdots \\ {X\left[{L - \lambda + N - 1} \right]}& {X\left[{L - \lambda + N} \right]}& \cdots & {X\left[{L - \lambda + N + M - 2} \right]} \end{array}} \right]$ | (10) |
数据矩阵H有长为M的频率窗口矢量信号X[k]的N个数据记录。
(2) 对矩阵H进行奇异值分解:H=USVH。
(3) 对矩阵V进行信号子空间和噪声子空间的分解:V=[Vs|Vn]。
这里,Vs是对应p个最大奇异值的右奇异矢量的矩阵。由于信号部分由用频率窗时间矢量s(t)作为模型的复指数的和构成,所以,矩阵S和Vs生成相同的子空间。因此,存在一个可逆变换T将Vs映射为S,即:S=VsT。
(4) 将信号子空间分成Vs两个较小的M-1维的子空间:
${{V}_{\rm{s}}} = \left[{\begin{array}{*{20}{c}} {{{V}_1}}\\ { * * \cdots * } \end{array}} \right] = \left[{\begin{array}{*{20}{c}} { * * \cdots * }\\ {{{V}_2}} \end{array}} \right]$
这里,V1和V2分别对应非交错的和交错的子空间。由于S1和S2对应相同的子空间,映射关系对这些子空间同样成立:S1=V1T,S2=V2T。
(5) 求解V1和V2之间的关系矩阵y。
矩阵S的非交错的和交错的分量通过子空间旋转j相关联。由于矩阵V1和V2同样分别生成这些相关的子空间,一个相似的联系V1和V2的(旋转)关系肯定存在:V2=V1y。求解矩阵y有如下两种方法:LS和TLS。
(a) LS解法
通过使用最小二乘(LS)准则解V2=V1y得到子空间的旋转的估计:yls=(V1HV1)-1V1HV2,这个LS解通过在一个最小二乘意义上从公式V2+
E2=V1y最小化误差得到,这里,E2是由V2和对应于S2的真实子空间之间的误差构成的矩阵。这个LS公式假定误差仅存在于对S2的估计中,而在V1和欲估计的相应于S1的真实子空间之间没有
误差。
(b) TLS解法
由于V1也是一个估计的子空间,一个更合适的公式是V2+E2=(V1+E1)y。这里,E1是表示V1和对应于S1的真实子空间之间的误差的矩阵。这个问题的解称为“总体最小二乘”(TLS)解,是通过最小化两个误差矩阵的Frobenius范数:${\left\| {{{{E}_1}} \quad {{{E}_2}}} \right\|_{\rm{F}}}$得到的。
将矩阵V1+E1和V2+E2并排放置后,可以得到方程[15]
| $\left[ {{{V}_1} + {{E}_1}} \quad {{{V}_2} + {{E}_2}} \right]\left[{\begin{array}{*{20}{c}} {ψ} \\ { - {{I}_p}} \end{array}} \right] = {0}$ | (10) |
将估计的信号子空间矩阵V1和V2并排放置并进行奇异值(SVD)分解:
| $\left[ {{{V}_1}} {{{V}_2}} \right] = \widetilde {U}\widetilde {Σ} {\widetilde {V}^{\rm{H}}}$ | (11) |
其中,
| $\widetilde {U} = \left[ {{{\widetilde {U}}_1}} \ {{{\widetilde {U}}_2}} \right]$,${}\widetilde {Σ} = \left[{\begin{array}{c} {{{\widetilde {Σ} }_1}}\ \ \,{0}\\ {0}\quad {{{\widetilde {Σ} }_2}} \end{array}} \right]$,$\widetilde {V} = \left[{\begin{array}{*{20}{c}} {{{\widetilde {V}}_{11}}}\ \ {{{\widetilde {V}}_{12}}}\\ {{{\widetilde {V}}_{21}}}\ \ {{{\widetilde {V}}_{22}}} \end{array}} \right]$ |
${\widetilde {U}_1}$和${\widetilde {U}_2}$为M×p阶矩阵,其余为p阶方阵。由最小Frobenius范数定理,可知
| ${\left\| { {{{E}_1}} \quad {{{E}_2}} } \right\|_{\rm{F}}} \ge \sum\limits_{i = p + 1}^{2p} {\sigma _i^2\left[{ {{{V}_1}} \quad {{{V}_2}} } \right]} $ | (12) |
其中si表示矩阵[V1 V2]的奇异值,及对角矩阵${}\widetilde {Σ} $中的元素。由于sp[V1 V2]>sp+1[V1 V2],两个误差矩阵的最小Frobenius范数具有唯一解。交错子空间并排放置矩阵[V1 V2]所张成的与脉冲相移相关的信号子空间矩阵为
| $\left\{ {\left[ {{{V}_1}}\quad {{{V}_2}} \right]} \right\} = {\widetilde {U}_1}{\widetilde {Σ} _1}\left[ {\widetilde {V}_{11}^{\rm{H}}}\quad {\widetilde {V}_{21}^{\rm{H}}} \right]$ | (13) |
此信号子空间矩阵的零空间是$\left[{\begin{array}{*{20}{c}} {{{\widetilde {V}}_{12}}}\\ {{{\widetilde {V}}_{22}}} \end{array}} \right]$的象空间。因此,从式(12)可知,对某个p阶方阵S,有
| $\left[{\begin{array}{*{20}{c}} {ψ} \\ { - {{I}_p}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{{\widetilde {V}}_{12}}}\\ {{{\widetilde {V}}_{22}}} \end{array}} \right]{S}$ | (14) |
从方程${}{ψ} = {\widetilde {V}_{12}}{S}$和$ - {{I}_p} = {\widetilde {V}_{22}}{S}$可看出${S} = - \widetilde {V}_{22}^{ - 1}$。因此必有
| ${ψ} = - {\widetilde {V}_{12}}\widetilde {V}_{22}^{ - 1} = {{ψ} _{{\rm{tls}}}}$ | (15) |
(6) 求解y的特征值
对矩阵S2: S2=V2T=V1yT,S2=S1j=V1Tj,那么yT=Tj,y=TjT-1。由于y与j有相同的特征值,j的特征值就是对角元素{ui}i=1,···,p。求解y的特征值,就能得到时间估计是:${\hat t_i} = \frac{{ - \angle {u_i}}}{{2{π} {f_0}}}$。同样,再由$X\left[k \right] = \sum\nolimits_{i = 1}^p {{d_i}{{\left( {{u_i}} \right)}^k}} $即可计算出信号的幅度di。
ESPRIT算法在计算过程中要经过奇异值分解和矩阵特征值求解,在特征值求解的过程中存在行列式计算和多项式求根的过程,其复杂度要比零化滤波算法大;无论是LS和TLS求解的过程都要经过1次矩阵乘法和1次矩阵求逆的运算,只是TLS求解过程中矩阵计算的阶数是LS求解过程的两倍,在计算复杂度上,LS过程要简单一些。
4 仿真分析本文对PPM-UWB信号的重建算法进行了仿真,发射脉冲波形选择高斯2阶脉冲,脉冲宽度为0.5 ns,带通滤波器的中心频率为fc=3.325 GHz,根据第2节和第3节中算法所需的频域采样点的多少,以及在相同时间长度下,频率分辨率不随采样率变化的特征,对信号码速率为20 Mbps和40 Mbps的波形进行了仿真;调制方式采用二进制的PPM调制,仿真过程中使用了106 bit进行了误码率的统计,进行重建算法的时候,每次截取了10个脉冲长度的时间进行处理。
针对20 Mbps的信号码速率,在零化滤波算法中,所需的最小的带通滤波器带宽为40 MHz;在ESPRIT算法中,若将噪声子空间的维度设为5,那么所需的最小的带通滤波器的带宽为50 MHz。针对40 Mbps的信号码速率,所需的最小的带通滤波器带宽为80 MHz。在性能方面,本文针对不同的带通滤波器的带宽,对两种算法的不同解在-3 dB的信噪比下进行了误码率性能对比,图 3和图 4是两种不同速率下的带宽性能对比结果。
 | 图 3 不同算法的带通滤波器带宽在20 Mbps的信号码速率下的性能对比(信噪比为-3 dB)Fig. 3 Different algorithms performance on band-pass filter bandwidth with 20 Mbps symbol rate (SNR is -3 dB) |
从图 3和图 4中可以看出,尽管ESPRIT算法所需的带通滤波器的最小带宽要比零化滤波算法大,但是在能够允许的相同带通滤波器的带宽下,ESPRIT算法的误码率性能要明显好于零化滤波算法,并且带宽越宽,ESPRIT算法的性能就越好。
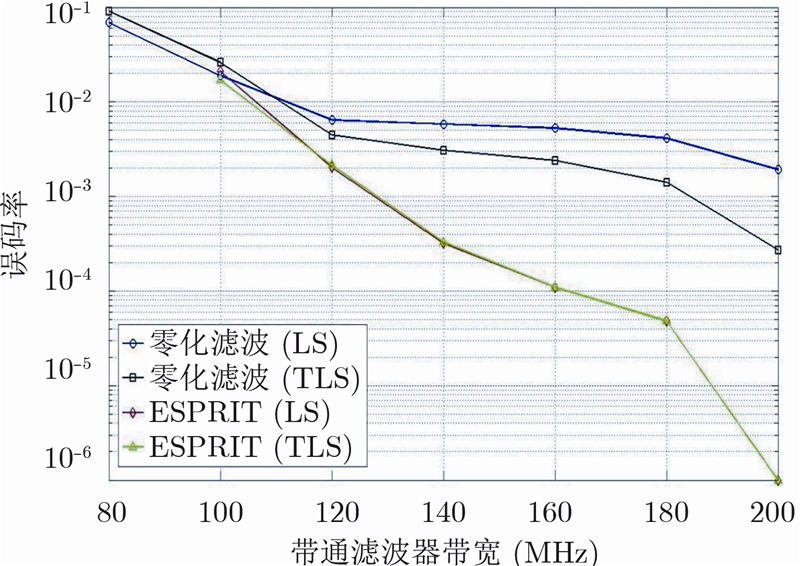 | 图 4 不同算法的带通滤波器带宽在40 Mbps的信号码速率下的性能对比(信噪比为-3 dB)Fig. 4 Different algorithms performance on band-pass filter bandwidth with 40 Mbps symbol rate (SNR is -3 dB) |
根据图 3和图 4的带宽性能,本文将20 Mbps的信号码速率下的80 MHz带宽的带通滤波器和40 Mbps的信号码速率下的160 MHz带宽的带通滤波器的数据进行了信噪比性能的仿真,图 5和图 6是仿真结果。
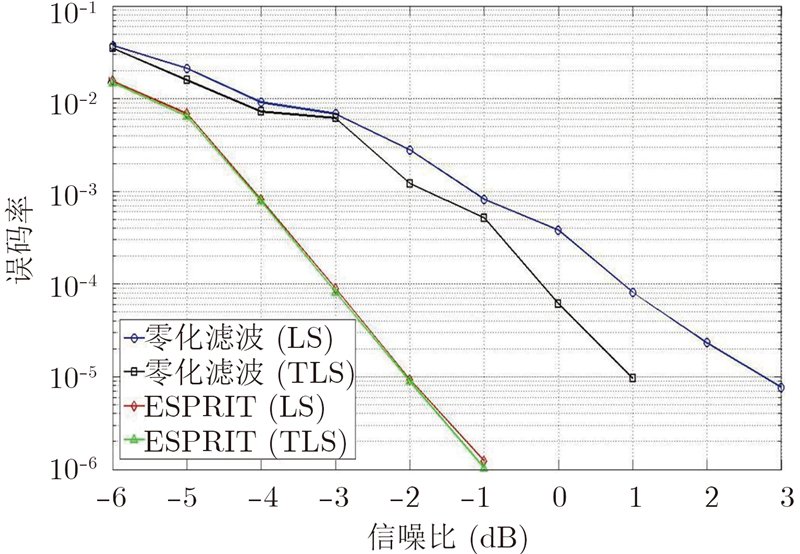 | 图 5 不同算法在20 Mbps的信号码速率下的信噪比性能对比(带通滤波器带宽为80 MHz)Fig. 5 Different algorithms performance on SNR with 20 Mbps symbol rate (band-pass filter bandwidth is 80 MHz) |
 | 图 6 不同算法在40 Mbps的信号码速率下的信噪比性能对比(带通滤波器带宽为160 MHz)Fig. 6 Different algorithms performance on SNR with 40 Mbps symbol rate (band-pass filter bandwidth is 160 MHz) |
从图 5和图 6中可以看出,ESPRIT算法的误码率性能比TLS解的零化滤波算法要高出2 dB,比LS解的零化滤波算法要高出4 dB。在图 3~图 6中,我们发现ESPRIT算法在LS解和TLS解方面的性能差别几乎没有,原因是在零化滤波算法中,TLS解同时考虑了不同时刻信号的噪声,LS解只考虑了某一时刻信号的噪声;在ESPRIT算法中则进行了噪声维度的设定,在设定噪声维度的时候就考虑了不同时刻信号的噪声。从第3节中的ESPRIT的LS和TLS的计算过程上看,LS解的计算量要明显少于TLS解,因此,ESPRIT算法的LS解的应用前景较大。
5 结论本文基于PPM-UWB带通欠采样信号进行了重建算法的探讨和分析,从频率分辨率的角度,在满足信号新息率的条件下,得出提高采样率并不能增加固定带通带宽内的频域采样点数,即不能提高系统性能。本文随后给出了零化滤波算法和ESPRIT算法的滤波器带宽和信噪比的性能,仿真结果表明,ESPRIT算法所需的最小带通滤波器的带宽比零化滤波算法略高,但是其具有在同等条件下明显高于零化滤波算法的性能,综合算法性能和计算过程来看,ESPRIT算法的LS解在工程中具有较大的应用前景。
| [1] | 杨峰, 胡剑浩, 李少谦. 欠采样技术的超宽带信号子空间重建方法[J]. 电子科技大学学报, 2010, 39(6): 841-844.
Yang Feng, Hu Jian-hao, and Li Shao-qian. Subspace reconstruction method of UWB signals based on sub-sampling[J]. Journal of University of Electronic Science and Technology of China, 2010, 39(6): 841-844. ( 1) 1) |
| [2] | 周田华, 何宁, 敖发良. 水下光通信PPM数字接收机的DSP实现[J]. 光学技术, 2006, 32(Suppl.): 607-609.
Zhou Tian-hua, He Ning, and Ao Fa-liang. The realization of PPM digital receiver with DSP in underwater optical communication[J]. Optical Technique, 2006, 32(Suppl.): 607-609. ( 1) 1) |
| [3] | 吴建军, 梁庆林, 项海格. 稀疏多径信道下非相干UWB-PPM接收机的多区积分优化方法[J]. 电子与信息学报, 2007, 29(9): 2168-2172.
Wu Jian-jun, Liang Qing-lin, and Xiang Hai-ge. Multiple sub-intervals integration period optimization for noncoherent UWB-PPM receiver in sparse multipath channels[J]. Journal of Electronics & Information Technology, 2007, 29(9): 2168-2172. ( 2) 2) |
| [4] | 陈海燕, 刘威, 李莉. 基于双滤波器的全光超宽带脉冲调制研究[J]. 光通信技术, 2014, 38(7): 17-19.
Chen Hai-yan, Liu Wei, and Li Li. Research of all-optical ultra wideband pulse modulation based on double filter[J]. Optical Communication Technology, 2014, 38(7): 17-19. ( 1) 1) |
| [5] | 裴志军, 孙守梅, 张平, 等. 基于有限更新率采样的UWB信号处理技术[J]. 天津工程师范学院学报, 2009, 19(3): 10-13.
Pei Zhi-jun, Sun Shou-mei, Zhang Ping, et al.. UWB signal processing based on sampling with finite rate of innovation[J]. Journal of Tianjin University of Technology and Education, 2009, 19(3): 10-13. ( 1) 1) |
| [6] | Vetterli M, Marziliano P, and Blu T. Sampling signals with finite rate of innovation[J]. IEEE Transactions on Signal Processing, 2002, 50(6): 1417-1428. ( 1) 1) |
| [7] | Maravic I and Vetterli M. Sampling and reconstruction of signals with finite rate of innovation in the presence of noise[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 2788-2805.( 1) 1) |
| [8] | Marziliano P, Vetterli M, and Blu T. Sampling and exact reconstruction of bandlimited signals with additive shot noise[J]. IEEE Transactions on Information Theory, 2006, 52(5): 2230-2233.( 1) 1) |
| [9] | Blu T, Dragotti P L, Vetterli M, et al.. Sparse sampling of signal innovation[J]. IEEE Signal Processing Magazine, 2008, 25(2): 31-40. ( 1) 1) |
| [10] | 杨峰, 胡剑浩, 李少谦. 基于欠奈奎斯特采样的超宽带信号总体最小二乘重建算法[J]. 电子与信息学报, 2010, 32(6): 1418-1422.
Yang Feng, Hu Jian-hao, and Li Shao-qian. A total least squares reconstruction algorithm of UWB signals based on sub-Nyquist sampling[J]. Journal of Electronics & Information Technology, 2010, 32(6): 1418-1422.( 1) 1) |
| [11] | 杨峰. 脉冲超宽带的欠采样方法研究[D]. [博士论文], 成都电子科技大学, 2010.
Yang Feng. Research on sub-Nyquist sampling methods for impluse-UWB communications[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2010. ( 1) 1) |
| [12] | 康晓非. 超宽带系统中接收技术研究[D]. [博士论文], 西安电子科技大学, 2012.
Kang Xiao-fei. Study on reception techniques for ultra wideband systems[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2012. ( 1) 1) |
| [13] | Ottersten B, Viberg M, and Kailath T. Performance analysis of the total least squares ESPRIT algorithm[J]. IEEE Transactions on Signal Processing, 1991, 39(5): 1122-1135. ( 1) 1) |
| [14] | Manolakis D G, Ingle V K, and Kogon S M. 统计与自适应信号处理[M]. 北京: 电子工业出版社, 2003: 465-470.
Manolakis D G, Ingle V K, and Kogon S M. Statistical and Adaptive Signal Processing[M]. Beijing: Publishing House of Electronics Industry, 2003: 465-470. ( 1) 1) |
| [15] | Golub G H and Van Loan C F. 矩阵计算(第3版)[M]. 北京: 人民邮电出版社, 2011: 532-533.
Golub G H and Van Loan C F. Matrix Computations (3rd Edition)[M]. Beijing: Posts and Telecom Press, 2011: 532-533.( 1) 1) |


