合成孔径雷达(SAR)是一种高分辨率2维微波成像雷达,在距离向通过发射宽带线性调频信号获取高分辨率,在方位向利用合成孔径原理获取高方位分辨率。SAR成像本质上是对距离、方位2维线性调频信号进行脉冲压缩处理[1, 2]。脉冲压缩技术就是对信号进行压缩滤波,将信号的能量集中在窄脉冲输出,可以利用相关法或去斜频率分析法实现[3]。采用相关法实现脉冲压缩时,需要把信号快速傅里叶变换(FFT)到频域,将信号频域与含有2次共轭相位的频域滤波器进行复乘,再IFFT变换到时域,因此需要2次FFT变换、1次复乘运算。去斜频率分析法采用频域滤波的方法实现脉冲压缩时,先在时域将信号与调频斜率相反的线性调频参考信号相乘,再FFT变换到时域,仅需要1次FFT变换、1次复乘运算。去斜频率分析法是通过去斜处理将线性调频信号转化为单频信号,由于单频信号的频率与输入信号位置相关,可通过FFT变换滤波实现对线性调频信号的压缩。去斜频率分析法的关键在于去斜处理,其核心就是将输入的线性调频信号与一个调频率大小相同但符号不同的参考信号相乘,去掉2次相位,得到单频信号。去斜频率分析法简单高效,可以采用数字的方法实现脉冲压缩,常常用于轻小型化SAR的实时成像处理技术中。
目前国内外典型轻小型化SAR均采用调频连续波(FMCW)技术[4, 5, 6, 7, 8, 9, 10]。FMCW SAR系统使用收发天线持续不断地发射和接收信号,其脉冲占空比为100%,可以减小系统对峰值功率的要求、简化模块设计,提高系统可靠性。大部分的小型化FMCW SAR系统采用了去斜处理[4, 5, 8, 9, 10],通过去斜技术可降低A/D 采样率,使后续的实时信号处理实现复杂度下降,同时也降低了系统的数据存储量要求。常用的去斜方式有两种,分别是接收端去斜和数字去斜,文献[4, 5, 8, 10]所述的MiSAR, BYU microSAR, CARMSAR,微型SAR/GMTI系统采用了接收端去斜,文献[9]所述的MiniSAR系统采用了数字去斜。接收端去斜要求模拟端微波器件具有较高的调频线性度和频率稳定度,对于宽带SAR系统来说,实现成本高而且系统复杂[11, 12]。数字去斜可以较容易地产生宽带线性调频信号,也有利于对非理想信号的误差补偿。但数字域去斜一般在中频进行,这样会增加A/D 采样设备、数据存储与处理设备的复杂度。本文提出了一种改进的数字去斜方法。利用该方法可以直接在视频以低于雷达系统发射信号带宽的采样频率对回波信号进行AD采样,然后在数字域完成去斜处理,本文方法降低了数据处理与存储的要求,提高了处理精度,能够适用于轻小型雷达系统。
本文首先介绍了去斜频率分析法实现脉冲压缩的原理,之后提出了改进的数字域去斜方法,对数字去斜方法进行数学推导,给出了采样频率的选取准则,并通过仿真验证了本文方法的正确性和有效性。
2 去斜频率分析法原理去斜频率分析法对线性调频信号进行脉冲压缩可以分为两步来理解:首先将线性调频回波信号与符号相反、调频斜率相同的线性调频参考信号相乘,转化为频率与信号输入位置成正比的正弦波,一般将这一步骤称为去斜处理[2]。经过去斜处理的信号,由于目标处于不同的位置,得到的信号频率也不相同,因此可以用FFT滤波的方法分析此信号的频率,由此区分不同位置的目标,实现对线性调频信号的压缩处理。
SAR系统发射线性调频信号时,S(t)为点目标的距离向回波信号,具体表达式见式(1)。其中调频斜率为Kr,信号持续时间为T0,信号带宽为B0,点目标所在的位置对应的时间为t0。
| $S(t) = \exp \{ - {\rm j}\pi {K_{\rm{r}}}{(t - {t_0})^2}\} , \\ \qquad \quad- {T_0}/2 + {t_0} \le t \le {T_0}/2 + {t_0}$ | (1) |
参考信号的位置位于t1,信号持续时间为T1,其调频斜率与点目标回波信号的调频斜率相同,而符号相反,可以表示为:
| ${S^*}(t) = \exp \{ - {\rm j}\pi {K_{\rm{r}}}{(t - {t_1})^2}\} \\ \qquad \quad- {T_1}/2 + {t_1} \le t \le {T_1}/2 + {t_1}$ | (2) |
两个信号经过混频后变为:
| $\eqalign{ & S(t){S^*}(t) = \exp \{ {\rm j}\pi {K_{\rm{r}}}2t({t_0} - {t_1})\} \cr & \qquad \qquad \quad \ \cdot \exp \{ {\rm j}\pi {K_{\rm{r}}}({t_0}^2 + {T_1}{t_0})\} \cr & \qquad \qquad \quad \ \cdot \exp \{ {\rm j}\pi {K_{\rm{r}}}( - {t_1}^2 - {T_1}{t_1})\} \cr & \qquad \qquad \quad \ \cdot \exp \{ {\rm j}\pi {K_{\rm{r}}}\{ 2{t_0}t{}_1\} \} \cr} $ | (3) |
通过式(3)我们可以看到,混频后的信号为一个复正弦波,其频率为Kr(t0-t1)。正弦波经过FFT变换后变为式(4),是一个sinc函数形式,表示目标的部分能量被压至FFT输出阵列的某一采样点上,其采样点位置由解斜后的频率决定,具体如式(5)所示。
| $\left| {S(q)} \right| = \left| {{{\sin \{ \pi {T_1}({K_{\rm{r}}}({t_0} - {t_1}) - q/{T_1})\} } \over {\sin \{ \pi ({K_{\rm{r}}}({t_0} - {t_1}) - q/{T_1}\} }}} \right|$ | (4) |
| $q = {K_{\rm{r}}}({t_0} - {t_1}){T_1}$ | (5) |
信号去斜后,由傅里叶变换的知识可以知道,对于时间宽度为T0的等频信号,经过傅里叶变换之后,其主瓣宽度即目标在频率域上的分辨率为式(6),则应的时间分辨率为式(7),由发射信号带宽决定。这样通过去斜、FFT处理恢复出来点目标的距离向信息。
| ${\rho _{\rm{f}}} = {1 \over {{T_0}}}$ | (6) |
| ${\rho _{\rm{t}}} = {{{\rho _{\rm{f}}}} \over K} = {1 \over {K{T_0}}} = {1 \over {{B_0}}}$ | (7) |
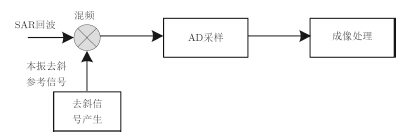
在SAR系统中,去斜的基本思想就是采用与调频率与发射信号相反的线性调频信号作为参考信号,与回波信号做差频处理,将回波信号与参考信号之间的时间差就转换成不同的差频频率。常用的去斜方式有两种,分别是接收端去斜和数字去斜。接收端去斜指在射频接收时,利用与发射信号符号相反的本振与SAR回波信号进行混频,在高频段完成去斜处理,原理如图 1所示[6, 7]。为避免混叠,数字去斜一般在中频进行,利用高采样率AD采集设备在中频进行采样,然后在数字域与参考信号复乘完成去斜处理。
|
图 1 接收端去斜原理图 Fig.1 Dechirp-on-reciever illustrative diagram |
接收端模拟去斜要求模拟器件具有较高的调频线性度和频率稳定度,对于宽带SAR系统来说实现成本高而且系统复杂。在数字去斜中,可以比较容易地产生宽带线性调频信号,也有利于对非理想信号的误差补偿,因此很多雷达系统常用数字去斜方法。但是在数字去斜中,如果参考信号的持续时间比回波信号持续时间短,会造成信号能量损失导致分辨率下降,要求参考信号的持续时间T1大于目标信号持续时间T0,加大了AD采样频率。例如,发射一个持续时间为10μs、信号带宽为600MHz的线性调频信号,若测绘宽度为1.5km时,对应回波长度至少为10μs。为了把所有的目标全分辨率恢复出来,意味着需要采用一个持续时间为20μs、调频斜率为-60MHz/μs、信号带宽为1.2GHz的线性调频信号为参考去斜信号。所以在常规的数字去斜系统中,一般在中频进行高速AD采样,这样增加了数据处理、存储的设计与实现难度。
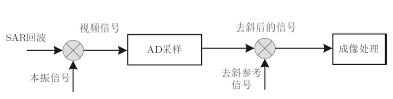
3.2 改进的数字去斜方法本文提出的数字去斜方法,直接在视频以低于雷达系统发射信号带宽的采样频率对回波信号进行AD采样、在数字域完成去斜。接收到的SAR回波信号经过混频、下变频到视频后,利用AD设备进行采样,转换为数字信号,然后在数字域与去斜参考复乘获得去斜数字信号,其原理框图如图 2所示。
|
图 2 改进的数字去斜方法原理图 Fig.2 Improved digital dechirp method illustrative diagram |
在SAR系统中,点目标的距离向回波信号下变频解调后:
| $S(t) = \exp \left[ {{\rm{j}}\pi {K_{\rm{r}}}{{(t - {t_0})}^2}} \right] \\ \qquad \quad- {T_0}/2 \le t - {t_0} \le {T_0}/2$ | (8) |
对信号进行低采样率AD变换,相当于信号与采样脉冲进行卷积:
| $${S_{\rm{p}}}(t) = \sum\limits_{n = - N/2 + 1}^{N/2} {S(n{t_{\rm{s}}})\delta (t - n{t_{\rm{s}}})} $$ | (9) |
去斜参考信号为:
| ${S_{{\rm{ref}}}}(t) = \exp \left( { - {\rm{j}}\pi {K_{\rm{r}}}{t^2}} \right) \\ \qquad \qquad - {T_1}/2 \le t \le {T_1}/2$ | (10) |
一般取 ${T_1} \ge {T_0}$,将去斜参考信号离散化,得到:
| ${S_{{\rm{pref}}}}(t) = \sum\limits_{m = - M/2 + 1}^{M/2} {{S_{{\rm{ref}}}}(m{t_{\rm{s}}})\delta (t - m{t_{\rm{s}}})} $ | (11) |
AD采样后的信号转换为离散时间序列后,与去斜参考信号去斜相乘得到:
| $\displaylines{ X(t) = {S_{\rm{p}}}(t){S_{{\rm{pref}}}}(t) \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \ = \sum\limits_{n = 0}^{N\! -\! 1} {S(n{t_{\rm{s}}})\delta (t \!-\! n{t_{\rm{s}}})} \sum\limits_{m = 0}^{M\! - \!1} {{S_{{\rm{ref}}}}(m{t_{\rm{s}}})\delta (t \! -\! m{t_{\rm{s}}})} \cr} $ | (12) |
令${Y_{\rm{p}}}(k)$为${S_{\rm{p}}}(t)$的FFT输出,${Y_{{\rm{pref}}}}(k)$为${S_{{\rm{pref}}}}(t)$的FFT输出,则根据驻定相位原理:
| $\displaylines{ {Y_{\rm{p}}}(k) \!=\! FFT\left\{ {{S_{\rm{p}}}(t)} \right\} \!\!\! \\ \qquad \quad \ \!=\! C \cdot {\rm{rect}}\left( {{f \over {{f_{\rm{s}}}}}} \right) \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ \cdot \exp \left( { \!- \! {\rm{j}}{{\pi {{\left( {k \cdot {\rm{df}}} \right)}^2}} \over {{K_{\rm{r}}}}} \!+\! {\rm{j}}{\pi \over 4} \!-\! {\rm{j}}2\pi k{t_0} \cdot {\rm{df}}} \right) \cr \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \!=\! C \cdot {\rm{rect}}\left( {{f \over {{f_{\rm{s}}}}}} \right)\exp \left\{ { \!- \! {\rm{j}}{\pi \over {{K_{\rm{r}}}}}{{\left( {k \cdot {\rm{df}} \!+\! {K_{\rm{r}}}{t_0}} \right)}^2}} \right\} \\ \qquad \qquad \qquad \qquad \qquad \ \cdot \exp \left\{ {j{\pi \over {{K_{\rm{r}}}}}{{\left( {{K_{\rm{r}}}{t_0}} \right)}^2} \!+\! j{\pi \over 4}} \right\} \cr} $ | (13) |
| $\displaylines{ & {Y_{{\rm{pref}}}}(k) = {\rm{FFT}}\left\{ {{S_{{\rm{pref}}}}(t)} \right\} \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad= C \cdot {\rm{rect}}\left( {{f \over {{f_{\rm{s}}}}}} \right) \exp \left( {j{{\pi {{\left( {kdf} \right)}^2}} \over {{K_{\rm{r}}}}} - j{\pi \over 4}} \right) \cr} $ | (14) |
为得到距离向位置信息需要对式(12)进行FFT运算,根据FFT的性质,X(t)的FFT变换相当于${Y_{\rm{p}}}(k)$与${Y_{{\rm{pref}}}}(k)$的圆周卷积,即:
| $Y(k) = {\rm{FFT}}\left\{ {X(t)} \right\} = {Y_{\rm{p}}}(k) * {Y_{{\rm{pref}}}}(k)$ | (15) |
如果信号采样时采样率fs低于信号带宽${B_0}$,那么在${S_{\rm{p}}}(t)$、${S_{{\rm{pref}}}}(t)$的频域会发生混叠,但是在圆周卷积过程中没有能量损失。${Y_{\rm{p}}}(k)$与${Y_{{\rm{pref}}}}(k)$的圆周卷积相当于两个符号相反的线性调频信号的卷积,其输出为一个sinc函数,具体表示为:
| $\displaylines{ Y(k) = {\rm{FFT}}\left\{ {X(t)} \right\} = {Y_{\rm{p}}}(k) * {Y_{{\rm{pref}}}}(k) \cr \qquad \, = G{{\mathop{\rm sinc}\nolimits} _K}\left\{ {{1 \over {{K_{\rm{r}}}}}{f_{\rm{s}}}\left( {k {\rm{df}} - {K_{\rm{r}}}{t_0}} \right)} \right\} \cr} $ | (16) |
式中:
| ${{\mathop{\rm sinc}\nolimits} _{K}}{\rm{ = }}{{\sin x} \over x}$ | (17) |
输出峰值位置为:
| $k{\rm{ = }}{K_{\rm{r}}}{t_0}/{\rm{df}} = {K_{\rm{r}}}{t_0}M{t_{\rm{s}}}$ | (18) |
只要输出位置不大于K,则压缩位置就不会混叠。即:
| $\left| {{K_{\rm{r}}}{t_{\rm{s}}}{t_0}} \right| = \left| {{{{K_{\rm{r}}}{t_0}} \over {{f_{\rm{s}}}}}} \right| < 1$ | (19) |
由公式(19)可以得到,当点目标回波信号数字去斜、FFT输出后,只要在频域的位置不大于采样频率fs,点目标是可分辨的。
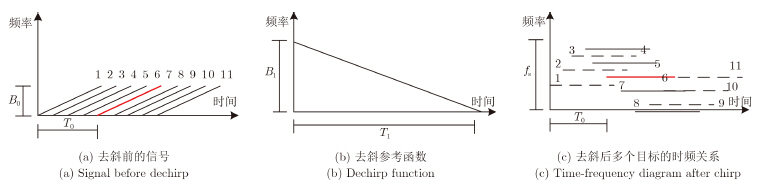
当距离向等间隔分布多个目标时,去斜前后的时频关系图如图 3所示[13]。从图 3中可以得到,为了能够对解调后的信号进行FFT压缩处理,经过去斜处理后,输出的信号频率不能大于采样频率fs,否则目标的频率会被相位相乘移至fs以外,混叠又会将其移到图 3(c)中的虚线位置,造成FFT输出后与其他目标混叠,无法正确恢复出它的位置信息。
|
图 3 去斜前后多目标的时频关系 Fig.3 Time-frequency diagram for dechirp of multi-target and non-dechirp multi-target |
当输入点目标回波信号与参考信号进行混频处理后,得到的单频信号频率只要低于系统采样频率,信号在频域就不会混叠,可准确的恢复出目标的位置信息。如果多点目标之间的位置很近,那么利用较低的采样率就可以恢复出所有的目标信息。当信号采样频率fs设计值高于所有输入点回波信号与参考信号混频后的单频信号频率时,即满足式(20),就能够满足数字去斜后脉冲压缩中对采样率的要求。式(20)中t0,t1分别为最近、最远的点目标回波信号与参考信号之间的时间间隔。
| $\left| {{K_{\rm{r}}}({t_0} - {t_1})} \right| \le {f_{\rm{s}}}$ | (20) |
通过以上分析,可以得到,若采用改进的数字去斜方法,当信号相对位置间隔小于发射信号脉冲宽度时,就能够以低于发射信号带宽的采样率对信号进行采样,全分辨率地恢复目标。
4 仿真分析在SAR系统中,若采用测绘带起始处为参考信号的起点即${t_0} = 0$,只要测绘带最远端的点目标与参考信号之间的频率差满足式(21),就能够对整个测绘带内的回波数据进行FFT滤波,无混叠地得到距离向图像。
| ${K_{\rm{r}}}{t_1} \le {f_{\rm{s}}}$ | (21) |
以测绘带起始处为参考信号的起点时,整个测绘带内的回波持续时间为${{2{w_{\rm{g}}}} \over {\rm{c}}}$,则式(21)变形为:
| ${{2{w_{\rm{g}}}} \over {\rm{c}}} \le {{{f_{\rm{s}}}} \over {{B_0}}}{T_0}$ | (22) |
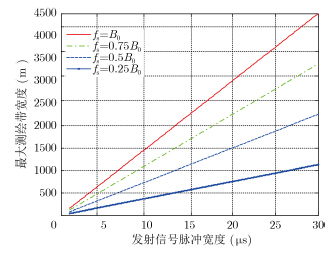
|
图 4 不同采样率下发射信号脉宽与测绘带内宽度的关系 Fig.4 Relation between pulse width and swath for different sampling rate |
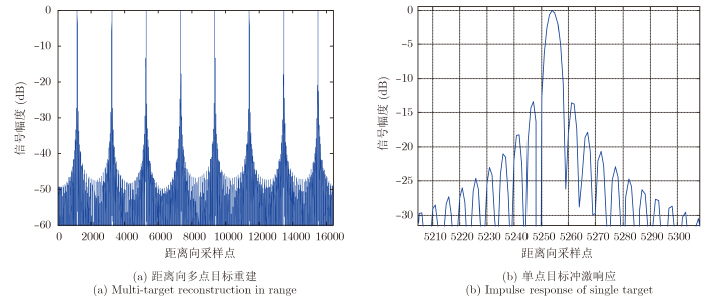
在SAR系统中,地面有效照射范围为1.5km,为获取0.3m高分辨率发射一个600MHz的线性调频信号,当发射信号持续时间分别为15μs、20μs时,根据图 5,仅需要分别采用450MHz、300MHz的采样频率进行采集与数字域去斜,利用频谱分析就可以恢复出条带内所有目标的距离向信息。如果不采用数字去斜方式,根据常规的数字去斜设计思想,至少需要采用600MHz的采样频率对回波信号进行采集。
|
图 5 沿距离向8个均匀布置的点目标谱分析压缩结果(fs=200MHz) Fig.5 Spectral analysis result of 8 targets uniformly distributed in range direction(fs=200MHz) |
本方法尤其适用于高频段的调频连续波轻小型化SAR系统。高频段调频连续波SAR系统一般作用距离近、为提高平均发射功率采用较长的发射脉冲,因此测绘带内回波持续时间会小于发射脉冲宽度。以ka波段调频连续波微小型化SAR系统为例,若作用距离5km时,对地照射的幅宽一般为1km左右。如果采用本文描述的数字去斜方法,当发射信号带宽600MHz,信号持续时间20μs时,系统的AD采样率可以设计为100MHz进行数字采集,保障了高分辨率的同时还降低了系统实现复杂度、利用数字处理提高了精度,有利于系统微小型化的实现。
因此在发射信号脉冲宽度能够覆盖整个测绘条带的轻小型SAR系统中,采用本文提出的数字去斜方法,可以选择采样率低于系统发射信号带宽的数字信号采集系统,降低信号采集设备、数字信号处理设备、数据存储设备的复杂度,降低系统实现难度。
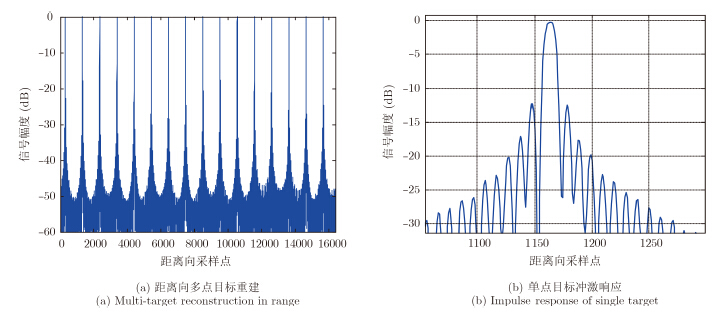
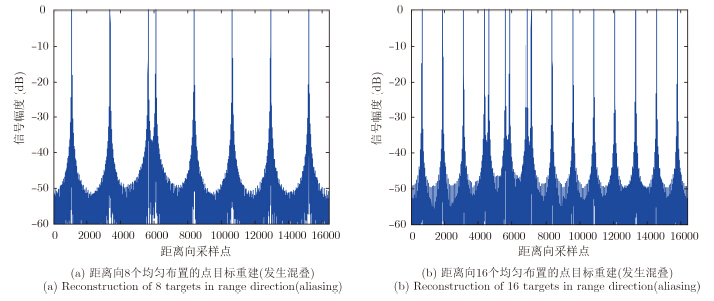
根据本文描述的数字去斜方法,我们进行了仿真实验。假设系统发射一个持续时间为16 μs,信号带宽为600 MHz的线性调频信号。根据式(22),若对回波信号分别为200 MHz, 400 MHz的降采样率进行数字采集,能够获取的最大条带分别为800 m, 1600 m。在每种采样率情况下,测绘带内沿距离向布置均匀摆放多个点目标,每个点目标距离间隔为100 m。图 5、图 6为去斜频率分析法的脉冲压缩处理结果。由图中可以看到,即使采用低于信号发射带宽的采样率对信号采集,在测绘带内也能够利用频率分析法对距离向的目标实现无混叠、全分辨率重建。图 7为测绘带宽较大时,即发射信号脉冲宽度无法覆盖整个测绘条带时,距离向多点目标去斜频率分析法的脉冲处理结果。由于不满足式(22),图中的多个均匀分布的点目标在处理后发生了混叠,无法正确恢复出各点的位置。
|
图 6 测绘带内沿距离向16个均匀布置的点目标谱分析压缩结果(fs=400MHz) Fig.6 Spectral analysis result of 16 targets uniformly distributed in range direction(fs=400MHz) |
|
图 7 测绘带宽较大时数字去斜后点目标谱分析压缩结果(fs=400MHz) Fig.7 Spectral analysis result after digital dechirp in large swath width (fs=400MHz) |
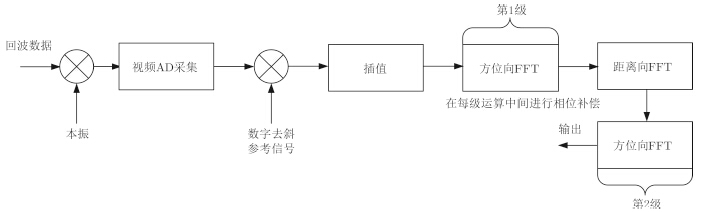
对于SAR成像而言,距离-多普勒、调频变标、谱分析、重叠子孔径算法(Overlapped Subaperture Algorithm, OSA)等SAR常用算法,其原理是经过2维的匹配滤波处理,得到2维sinc函数。以基于频率分析法原理的OSA为例,利用本文提出的数字去斜方法得到的SAR回波数据,采用OSA成像处理的流程如图 8所示[14],其中距离向采用数字去斜与FFT处理,方位向采用两级子孔径处理。
|
图 8 改进的数字域去斜OSA成像方法流程图 Fig.8 OSA image formation procedure for improved digital dechirp |
本文提出了一种用于SAR的数字去斜方法。利用本文方法,在SAR系统中,通过合理选取发射信号带宽与脉冲宽度,可以用低于发射信号带宽的采样率对SAR回波信号进行AD采集,然后在数字域进行去斜、完成距离向的频率分析法成像处理。本文方法与接收端去斜方法相比,不用额外的去斜信号生成设备、也避免了模拟器件的失真问题,在数字域去斜能够对非理想因素进行误差补偿、提高了处理精度,与常规的中频数字域去斜相比降低了采样率、减小了AD采集设备、数据存储设备、数据处理的实现难度,能够应用于轻小型化SAR系统中。尤其在高频段的近作用距离、高分辨率调频连续波SAR系统中,这种方法为系统的轻小型化实现提供了解决途径。
| [1] | Curlander J C and McDonough R N. Synthetic Aperture Radar: System and Signal Processing[M] , New York. Wiley. 1991: Chapter 1.( 1) 1) |
| [2] | 李春升, 杨威, 王鹏波. 星载SAR成像处理算法综述[J] , 雷达学报, 2013, 2(1):111-122. Li Chun-sheng, Yang Wei, and Wang Peng-bo. A review of spaceborne SAR algorithm for image formation[J]. Journal of Radars, 2013, 2(1): 111–122.(  2) 2) |
| [3] | Lacomme P, Hardange J P, Marchais J C, et al.. Air and Spaceborne Radar Systems: An Introduction[M] , US, William Andrew, 2001: Chapter 14.( 1) 1) |
| [4] | Edrich M and Weiss G. Second-generation Ka-band UAV SAR system[C] , Proceedings of the 38th European Microwave Conference, Amsterdam, 2008:1636-1639.( 3) 3) |
| [5] | Evan C, Zaugg Z and David G L. Theory and application of motion compensation for LFM-CW SAR[J] , IEEE Transactions on Geosciense & Remote Sensing., 2008, 46(10):2990-2998.( 3) 3) |
| [6] | Otten M, Van Rossum W, and Van Der Graaf M. Multichannel imaging with the AMBER FMCW SAR[C]. European Conference on Synthetic Aperture Radar, Berlin, 2014: 209-212.( 2) 2) |
| [7] | Acevo-Herrea R, Aguasca A, Mallorqui J J, et al.. High-compacted FM-CW SAR for boarding on small UAVS[C]. International Geoscience and Remote Sensing Symposium, 2009(2):543-546.( 2) 2) |
| [8] | Liu Yue and Deng Yunkai. CARMSAR-a Compact and Reconfigurable Miniature SAR system for high resolution remote sensing[C] , European Conference on Synthetic Aperture Radar, Nuremberg, 2012:294-297.( 3) 3) |
| [9] | 董勇伟, 梁兴东, 丁赤飚. 调频连续波SAR数字接收机技术研究[J] , 数据采集与处理, 2009, 24(S):69-73. Dong Yong-wei, Liang Xing-dong, and Ding Chi-biao. Research on FMCW SAR digital receiver[J]. Journal of Data Acquisition & Processing, 2009, 24(S): 69–73.(  3) 3) |
| [10] | 高许岗, 雍延梅. 无人机载微型SAR系统设计与实现[J] , 雷达科学与技术,2014,12(1): 35-38. Gao Xu-gang and Yong Yan-mei. Design and realization of UAV high resolution miniature SAR[J]. Radar Science and Technology, 2014, 12(1): 35–38.(  3) 3) |
| [11] | 金胜, 朱天林, 邓振淼, 等, 基于去斜的步进频合成高分辨距离像新方法[J] , 系统工程与电子技术, 2012, 34(6):1126-1130. Jin Sheng, Zhu Tian-lin, Deng Zhen-miao, et al.. Dechirp-based method for synthesizing high resolution range profle(HRRP) via stepped frequency waveforms[J]. Systems Engineering and Electronics, 2012, 34(6): 1126–1130.(  1) 1) |
| [12] | 江碧涛, 张云华, 姜景山, 宽带调频步进信号的全去斜处理方法[J] , 测试技术学报, 2008, 22(3):225-230. Jiang Bi-tao, Zhang Yun-hua, and Jiang Jing-shan. A De-Chirp processing method for wide-band stepped-frequency chirp signals[J]. Journal of Test and Measurement Technology, 2008, 22(3): 225–230.(  1) 1) |
| [13] | Cumming I G and Wong F H. Digital processing of synthetic aperture radar data[M]. Norwood, MA, Artech House, 2005: Chapter 9.( 1) 1) |
| [14] | 詹学丽, 王岩飞, 王超, 等. 一种基于脉冲压缩的机载条带SAR重叠子孔径实时成像算法[J] , 雷达学报, DOI: 10.12000/JR14126.. Zhan Xue-li, Wang Yan-fei, Wang Chao, et al.. Research on overlapped subaperture real-time imaing algorithm for pulse compression airborne strip SAR system[J]. Journal of Radars, DOI: 10.12000/JR14126.(  1) 1) |
 2015, Vol. 4 Issue (4) 474-480
2015, Vol. 4 Issue (4) 474-480
