传统合成孔径雷达（Synthetic Aperture Radar,SAR)在航迹向上通过平台运动实现天线的合成孔径，获得分辨能力，在波传播方向上通过宽带信号获得分辨能力，从而实现对观测场景的2维成像。由于采用单天线结构，它存在机下盲点、跨航向模糊和几何失真等问题^[1]。机载3维SAR通过在跨航向上分布阵列天线增加了跨航向的分辨能力，不仅克服了上述问题，而且能够获取目标的3维位置及散射信息，实现对观测场景的3维成像^{[2, 3]}，因此广泛应用于灾害监测、山区搜索和城市测绘等领域^[4]。目前对机载3维SAR开展的研究主要集中在成像算法方面，一般假设平台沿直线匀速运动^{[5, 6, 7, 8, 9, 10, 11, 12, 13]}。事实上，平台运动中受外部环境及自身振动等干扰，会产生包括平动误差和姿态角误差在内的运动误差，造成天线相位中心的偏移，影响成像质量，需进行补偿。对于传统SAR，姿态角误差对成像没有影响，只需补偿平动误差^[14]。对于3维SAR，平动误差导致的相位中心偏移在不同天线阵元间是一样的，可以通过传统SAR的运动补偿方法进行补偿；但姿态角误差导致的相位中心偏移在阵元间不同，无法用上述方法进行补偿。因此机载3维SAR运动补偿研究应着重于姿态角误差的补偿。文献^[15]利用自聚焦算法从回波数据中提取误差信息并进行补偿。但当姿态角误差较大时，基于回波数据的补偿方法效果有限，需结合测量数据进一步补偿。目前还没有基于测量数据的3维SAR运动补偿方法。此外，姿态角中偏航角的影响较横滚角更复杂。因此本文研究基于测量数据的机载3维SAR偏航角误差补偿方法。

本文首先建立了机载3维SAR成像和回波模型，接着分析了姿态角误差的影响，比较了横滚角误差和偏航角误差的影响，分析了偏航角导致的距离误差与航迹向波数、跨航向波数的关系，提出在航迹向和跨航向2维波数域分块计算距离误差，在3维空域逐块补偿的波数域子孔径补偿方法。最后通过仿真验证该方法可有效补偿偏航角运动误差的影响。 2 机载3维SAR成像模型

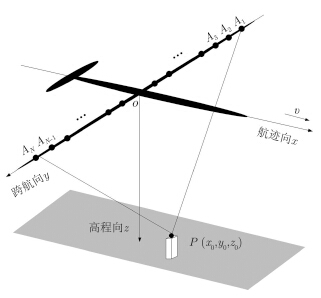
当不存在运动误差时，机载3维SAR的成像模型如图 1所示。其中，阵列天线沿跨航向y轴对称分布，其等效相位中心的坐标为(x, y_n, 0)，点目标P位于(x₀, y₀, z₀)，两者距离R如式(1)所示。经解调和匹配滤波后的回波如式(2)所示，其中c为光速，l为中心波长。将回波变换到3维波数域，进行STOLT插值后，再反变换到3维空域，就完成了3维成像。

图 1(Fig.1)

图 1 无运动误差时成像几何模型 Fig.1 Imaging model without motion errors

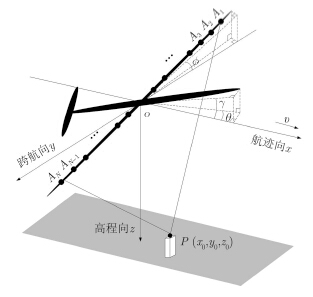
实际工作中，载机平台受到外界环境及自身振动等影响，会偏离理想航线，产生运动误差，需进行补偿。运动误差包括平动误差和姿态角误差，其中平动误差可通过传统单天线SAR运动补偿方法去除，但姿态角误差还没有有效的基于测量数据的补偿方法。如图 2所示，姿态角误差包括横滚角$\phi$，偏航角$θ$和俯仰角$γ$。其中俯仰角误差对成像没有影响^[15]。横滚角误差导致阵列天线在$yoz$平面内发生旋转，但不会在$x$方向引入运动误差，其在$yoz$平面内的成像结果聚焦正确，只是成像位置发生了对应旋转。这一影响可以通过控制点的引入和图像的几何变换进行补偿，补偿后再沿着x方向进行合成孔径处理即可完成3维成像。偏航角误差导致阵列天线在$xoy$平面内发生旋转，同时引入x和y两个方向的运动误差，在$xoz$和$yoz$平面内都无法得到聚焦正确的成像结果，需分别沿航迹向$x$和跨航向$y$进行补偿，较横滚角误差的补偿更为复杂。本文即研究偏航角误差的补偿方法。此时令$\phi=γ=0$，等效相位中心的坐标变为(x$-$y_nsinθ,y_ncosθ,0)，到点目标的距离RD及相对于R的距离误差ΔR分别如式(3)和式(4)所示。经解调和匹配滤波后的回波如式(5)所示。运动补偿的目的就是补偿距离误差ΔR的影响。以下推导基于测量数据的偏航角误差补偿方法。

图 2(Fig.2)

图 2 存在姿态角误差时成像几何模型 Fig.2 Imaging model with motion errors

如式(4)所示，距离误差ΔR受目标坐标x0和y₀的空变影响，无法在空域或波数域进行全孔径的补偿处理，因此考虑子孔径补偿方法。空域子孔径补偿方法是将回波数据在空域同时沿跨航向和航迹向分为多个较小子块，每个子块内假设y₀和θ为常数，补偿对应的ΔR后再2维拼接为全孔径^[16]。但在捷变运动误差情况下，每个航迹向子块内θ变化较大，若仍按常数处理，会残留较大误差。同时，跨航向的阵列长度远小于场景范围，划分子块后无法补偿阵列长度范围外目标导致的距离误差。因此空域子孔径补偿方法不适用于偏航角误差补偿。下面通过分析距离误差ΔR与航迹向波数k_x以及跨航向波数k_y之间的关系来推导波数域子孔径补偿方法。

将式(5)中的相位Ψ_Δ分别对x和y_n求偏导，可得到航迹向波数k_x和跨航向波数k_y，如式(6)和式(7)所示，其中f(x)=dθ/(dx)代表偏航角误差沿航迹向求导数。

由式(6)和式(7)解得x₀和y₀为

将x₀和y₀代入式(4)计算距离误差ΔR。如式(10)所示，ΔR与目标位置无关，即消除了目标的空变影响。其中ΔR₁代表ΔR第1项，ΔR₂为ΔR第2项与第3项之和。

首先补偿ΔR₁。由于ΔR₁与波数无关，可在回波3维空域进行补偿。由于阵列较短，y_n较小，ΔR₁远小于距离分辨单元，其包络误差可以忽略，相位误差可通过乘以滤波器$H_1$进行补偿，称为1次补偿。$H_1$如式(11)所示。

再补偿ΔR₂。由于ΔR₂与波数k_x,k_y一一对应，可在2维波数域分块计算；当子块划分较小时，子块内k_x,k_y变化较小，可认为近似不变，则ΔR₂仅随$x,θ,R_Δ$,y_n变化，可在空域精确补偿。补偿步骤如下：首先，将补偿完ΔR₁后的回波数据变换到航迹向和跨航向2维波数域，沿航迹向和跨航向分别均匀分为M和N段，得到MN个子块，每个子块内用中心波数k_xic,k_yjc代替k_x,k_y计算ΔR_2ij，如式(12)所示，其中i,j代表子块序号。

再将每个子块补零扩展到原尺寸，并变换到航迹向跨航向2维空域、距离向波数域，如式(13)所示，其中k_t代表距离向波数，k_tc为中心波数，B_kt为带宽。接着乘以滤波器H_2ij(如式(14)所示)补偿ΔR_2ij导致的相位误差，称为2次补偿。再变换到3维空域，此时每个子块都完成了距离误差ΔR_ij的补偿，如式(15)所示。最后将每个子块补偿后的数据直接相加，就得到全部回波补偿完ΔR后的结果。

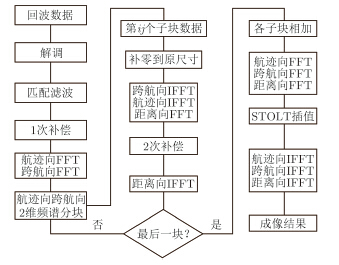
至此已完成距离误差ΔR的补偿。由于ΔR₂是在2维波数域分块计算的，称这种方法为波数域子孔径补偿方法。接着使用3维波数算法进行成像。即将数据变换到3维波数域后，进行STOLT插值，使航迹向、跨航向和高程向的波数均匀分布，再变换到3维空域后就得到聚焦正确的3维成像结果，如式(18)所示。插值前后的表达式分别如式(16)和式(17)所示。其中${k_z} = \sqrt {4k_t^2 + k_x^2 + k_y^2}$代表高程向波数，k_zc为中心波数，B_kz为带宽。运动误差补偿及成像处理流程如图 3所示。

图 3(Fig.3)

图 3 运动误差补偿及成像处理流程图 Fig.3 Flow chart of motion compensation and imaging

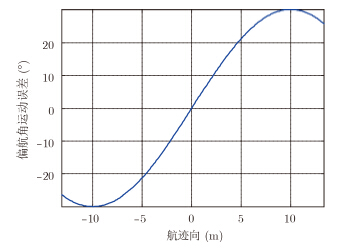
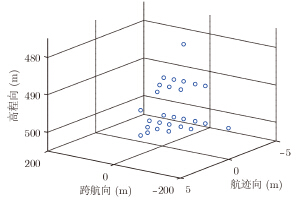
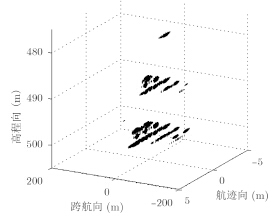
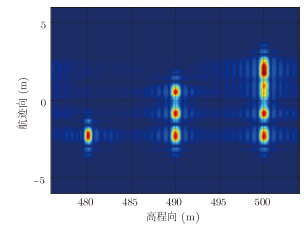
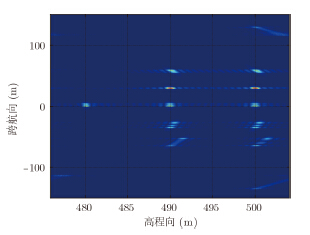
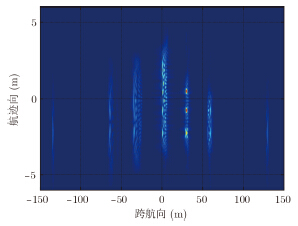
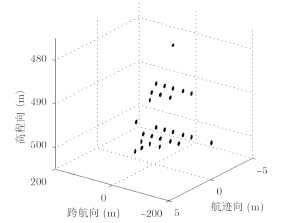
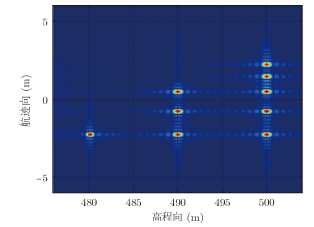
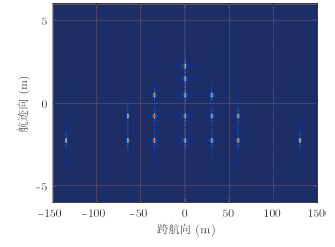
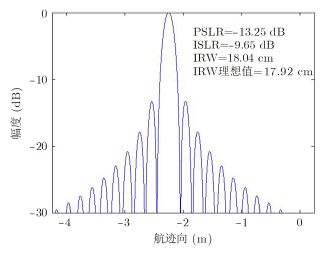
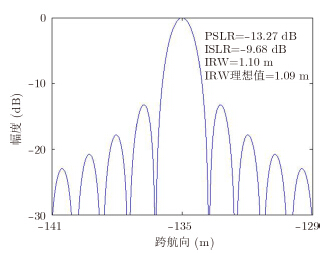
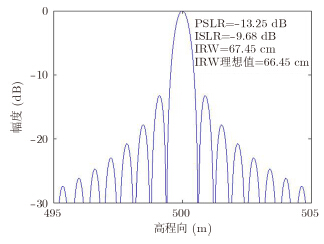
为了验证运动补偿方法的有效性，进行点目标成像仿真验证。仿真参数如表 1所示，加入如图 4所示的偏航角运动误差，其幅度为30°，频率为1Hz。27个点目标分3层排列，如图 5所示。图 6,图 7,图 8,图 9为运动补偿前点目标的3维成像结果及其在3个方向的切片，可见由于偏航角误差的影响，成像结果存在散焦，航迹向上尤为严重。运动补偿后的3维成像结果如图 10所示，其3个方向的切片如图 11,图 12,图 13所示。此时目标聚焦良好，位置正确。对场景边缘点(-2.25,-135,500)进一步考察成像指标，其3个方向的点扩展函数如图 14,图 15,图 16所示，峰值旁瓣比PSLR、积分旁瓣比ISLR和分辨率IRW都接近理想值，验证了补偿方法的有效性。

表 1(Tab. 1)

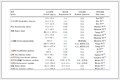
表 1 仿真参数Tab. 1 Simulation parameters 参数名称 数值 参数名称 数值 载波频率 17 GHz 飞行速度 40 m/s 信号波长 17.6 mm 飞行高度 500 m 信号带宽 200 MHz 发射天线数量 2 航迹向波束宽度 2.5° 接收天线数量 128 跨航向波束宽度 30° 天线孔径 40.44 cm 脉冲重复频率 300 Hz 等效相位中心间距 1.40 cm 脉冲持续时间 1 μs 偏航角运动误差 30°sin(2πt)

表 1 仿真参数 Tab. 1 Simulation parameters

图 4(Fig.4)

图 4 偏航角运动误差变化规律 Fig.4 Variation of yaw angle error

图 5(Fig.5)

图 5 点目标分布示意图 Fig.5 Distribution of point targets

图 6(Fig.6)

图 6 补偿前3维成像结果 Fig.6 3-D imaging result before compensation

图 7(Fig.7)

图 7 补偿前航迹向-高程向切片@跨航向0m Fig.7 Along-track height slide at cross-track 0m before compensation

图 8(Fig.8)

图 8 补偿前跨航向-高程向切片@航迹向–2.25m Fig.8 Cross-track height slide at along-track –2.25m before compensation

图 9(Fig.9)

图 9 补偿前航迹向-跨航向切片@高程向500m Fig.9 Along-and cross-track slide at height 500m before compensation

图 10(Fig.10)

图 10 补偿后3维成像结果 Fig.10 3-D imaging result after compensation

图 11(Fig.11)

图 11 补偿后航迹向-高程向切片@跨航向0m Fig.11 Along-track height slide at cross-track 0m after compensation

图 12(Fig.12)

图 12 补偿后跨航向-高程向切片@航迹向–2.25m Fig.12 Cross-track height slide at along-track –2.25m after compensation

图 13(Fig.13)

图 13 补偿后航迹向-跨航向切片@高程向500m Fig.13 Along-and cross-track slide at height 500m after compensation

图 14(Fig.14)

图 14 航迹向点扩展函数 Fig.14 Along-track point spread function

图 15(Fig.15)

图 15 跨航向点扩展函数 Fig.15 Cross-track point spread function

图 16(Fig.16)

图 16 高程向点扩展函数 Fig.16 Height point spread function

机载3维SAR通过合成孔径、阵列天线和宽带信号实现3维成像，但平台的运动误差会影响成像质量。其中姿态角误差影响复杂，难以通过常规的单天线SAR运动补偿方法去除。该文建立了机载3维SAR成像及误差模型，分析了姿态角误差对距离误差及成像的影响，发现偏航角误差影响最为复杂。对回波相位沿航迹向和跨航向分别求偏导，可得到航迹向和跨航向波数，它们与目标位置存在着对应关系，可用于求解距离误差。此时该误差与目标位置无关，消除了误差的空变影响。因此将回波在2维波数域分块，每个子块内固定波数、计算距离误差，并在空域逐块进行补偿。仿真结果验证了该方法的有效性。