信号时差参数估计问题是一个研究已久的课题,也是现代信号处理中信号检测与提取环节中一个重要组成部分。时差估计主要应用于无源定位[1]以及非合作性通信信号中。在无源定位众多方法中,时差测量法是一种精密测向方法[2]。时差定位是利用空间中多个接收机测出同一个辐射源信号到达各接收机的到达时间差,由此确定辐射源在空间中的位置。由于时差测向定位系统具有信号适应能力强、所需通道数量少、对天线方向图要求不苛刻、定位精度高等优点,因此特别适用于天线体制复杂、频率未知、跳变的复合调制雷达信号等情况。
雷达信号脉内复合调制形式[3]主要包含以下几种:频移键控与线性调频组合(FSK-LFM)、频移键控与二相编码组合(FSK-BPSK) 、频移键控与四相编码组合(FSK-QPSK)等。一个复合调制脉冲信号包含若干个时域等长,调制参数一致的子脉冲。这样的发射参数设置有利于雷达信号的相参积累,满足雷达解距离、速度模糊的条件要求,提高了雷达信号处理效率。随着现代战争电磁环境复杂性的增加,传统常规调制雷达信号已经不能满足战场需求,复合调制信号相比于常规调制信号拥有更多优点,已经在现代雷达中得到了广泛运用。因此,对于复合调制雷达信号时延量高精度估计的意义十分重大。
本文以FSK-BPSK复合调制雷达信号[4]为典型代表,提出了一种针对复合调制雷达信号的时差估计算法——相关函数拟合算法。该算法首先根据理论推导,将FSK-BPSK复合调制信号相关函数通过多段子脉冲相关函数和的形式表示[5]。同时FSK-BPSK复合调制信号子脉冲的频率对称分布特点和子脉冲时域长度一致等特点决定了相关函数中复杂不易计算的信号虚部可以被消除,仅仅保留便于计算的信号实部信息。最后将FSK-BPSK复合调制信号相关函数结果曲线与信号时差相关特性曲线相拟合,伴随时差值的1维搜索,当相关函数拟合误差达到最小时的时差遍历值即为时差估计值。仿真实验表明,本文提出的相关函数拟合算法在信噪比较低情况下,估计精度较高,且适用于带宽较小的复合调制信号时差估计情况。
2 信号模型由于FSK-BPSK复合调制信号具有大时宽带宽积,高分辨率优点和低截获概率特性,在雷达信号处理领域吸引了越来越多的关注。本文以FSK-BPSK信号[3]为一种特殊的复合调制雷达信号为例,讨论这类特殊信号的时差估计算法。
FSK-BPSK信号的解析形式为:
| $\begin{aligned} s\left( t \right) = & \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {A\exp \left\{ {{\rm{j}}2{π} {f \!_m}\left[{t - \left( {m - 1} \right){T_m}} \right.} \right.} } \\ & \left. {\left. { - \left( {n - 1} \right){T_n}} \right] + {\varphi _{mn}}} \right\} \end{aligned}$ | (1) |
式中fm为频率编码函数,m为子脉冲个数,n为子脉冲内码元个数,jmn=(0,p)为随机二相编码函数,子脉冲时宽为Tm,令设子脉冲带宽为Bw,采样频率为fs,采样间隔${T_s}$=1/fs,码元时宽Tn=
1/Bw。
信号的每一个子脉冲频率处在不同的频率编码频点,在各子脉冲内部进行随机相位编码调制[6],因为频率调制函数是相位调制函数的导数,所以在码元相位发生跳变的位置会造成信号频率的突变。
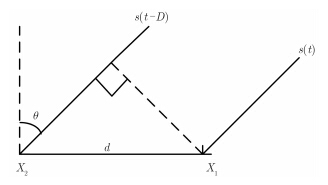
3 时差估计算法 3.1 信号相关特性远场模型[7]是指接收机之间的距离相对于辐射源之间的距离可忽略,两个接收通道接收的信号是平行入射的,如图 1所示。其中,d为接收机之间的距离,θ为信号的入射角,s(t$-$D)为s(t)的延时信号。
|
图 1 时差估计的远场模型 Fig.1 The far-field model of TDOA estimation |
时差估计的经典方法为基本相关法[8]。它是指利用两路信号之间的相关性,通过相关性叠加得到峰值对应的时间点为时差估计值。根据图 1双通道接收模型,接收到的两路信号可表示为:
| $\left. {\begin{array}{*{20}{l}} {x(t) = s(t) + {n_1}(t)}\\ {y(t) = s(t - D) + {n_2}(t)} \end{array}} \right\}$ | (2) |
| $\begin{aligned} {R_{xy}}(\tau ) = & E[x(t){y^*}(t + \tau )]\\ \quad \quad = & E[s(t){s^*}(t - D + \tau )] + E[s(t){n_2^*}(t + \tau )] \\ & + E[{n_1}(t){s^*}(t - D + \tau )] + E[{n_1}(t){n_2^*}(t + \tau )]\\ \quad \quad = & {R_{ss}}(\tau \! - \! D) \! + \! {R_{s{n_2}}}(\tau ) \! + \! {R_{{n_1}s}}(\tau - D) \! + \! {R_{{n_1}{n_2}}}(\tau ) \end{aligned}$ | (3) |
由于n1(t)和n2(t)及s(t)和s(t$-$D)相互之间是独立的,那么式(3)化简为:
| ${R_{xy}}(\tau ) = {R_{ss}}(\tau - D) = \int_0^T {x(t){y^*}\left( {t + \tau } \right)} {\rm{d}}t$ | (4) |
根据相关函数的性质,${R_{xy}}(\tau - D) \le {R_{xy}}(0)$,所以,时差值t=D即为Rxy最大值所对应的时间点。即:
| $\begin{aligned}\phi (\hat D) = & \mathop {\arg \max }\limits_\tau \phi (\tau ) = \mathop {\arg \max }\limits_\tau \int_0^T {x(t){y^*}\left( {t + \tau } \right)} {\rm{d}}t \\ = & \mathop {\arg \max }\limits_\tau {R_{ss}}(\tau - D)\end{aligned}$ | (5) |
基本相关算法原理简单,易于理解。但是它要求信号和噪声相互独立,且对非平稳信号和可变误差的时差估计误差较大。由于在实际信号相关运算过程中,计算机只能处理离散信号。采样频率决定了信号的离散化程度,同时采样频率${f_s}$也直接决定了信号采样间隔${△}T \;$,两者关系如下式:
| $△T = {1 \mathord{\left/ {\vphantom {1 {{f \!_{s}}}}} \right. } {{f\!_s}}}$ | (6) |
在实际操作过程中,采样频率过低往往不能满足时差估计精度要求,而采样频率过高则对于硬件要求很高。通过时差值t的1维搜索并代入相关函数式(4)中可得到一条信号相关特性曲线,曲线向量表示形式为S1,在S1最大值处可粗略得出时差估计值$\hat \tau $,但由于此时的时差估计值$\hat \tau $误差较大,因此可在曲线峰值的小范围区间内采用插值方法[9]求得更为精确的时差估计值$\hat \tau $。
插值方法可提高局部范围内时差估计分辨率,从而提高时差估计准确性,减小估计误差。但由于本文针对的特殊信号,插值函数与实际相关函数在模型上有一定的误差[10],再加上数字采样带来的系统误差,因此,时差估计的准确性有待提高。
3.2 FSK-BPSK复合调制信号相关函数FSK-BPSK复合调制信号是将发射的宽脉冲分为若干个调制参数一致、载频对称分布的子脉冲。两个接收通道接收的FSK-BPSK信号子脉冲q(t)为常规BPSK信号,子脉冲互相关函数Q(△)可表示为:
| $\begin{aligned} Q(△){\rm{ = }} & \int {\left[{q(t) + {n_1}(t)} \right]} \left[{{q^*}(t + d -△ ) } \right.\\ & + \left. {{n_2^*}(t +△)} \right]{\rm{d}}t = {R_{qq}}(d -△) \end{aligned}$ | (7) |
式(7)中△为真实时延值,是一个未知量,d为式(4)中时差值t在时域区间[-T,+T]内按照采样间隔△T提取的延时量样值。为方便函数计算,不失一般性,可令信号幅值A=1,式(7)展开计算:
| $\begin{aligned} Q(△) = & \sum\limits_{n = 1}^N {A\exp \{ {\rm{j}}2{π} {f \!_1}[t - (n - 1){T_n}] + {\varphi _{mn}}\} } \\ & \cdot \sum\limits_{n = 1}^N \! {A \! \exp \{ - {\rm{j}}2{π} {f \!_1}[\left( {t \! +\! d \! - \! △} \right) \! - \! (n \! - \! 1){T_n}] \! \! - \! \! {\varphi _{mn}} \} } \\ \quad \quad = & \frac{{{T_n} - \left| {d -△} \right|}}{{{T_n}}} \cdot \exp \left[{{\rm{j}}2{\rm {\pi}} {f \!_1}(d - △)} \right] \end{aligned}$ | (8) |
由于在几米基线长度条件下的时差值为纳秒量级,而信号时域长度一般为微秒量级[11],可认为时差值远远小于脉冲长度,在做相关运算时可忽略由于时延造成移位的采样点数相关值。因此两路脉冲信号的互相关函数结果$F(△\left| d \right.)$可用子脉冲相关函数和的形式近似表示,表达式如式(9):
| $\begin{aligned} F(△\left| d \right.) = & \sum\limits_{i = 1}^M {Q(△)} = \sum\limits_{i = 1}^M {{R_{qq}}(d - △)} \,\\ = & \frac{{{T_n} - \left| {(d - △)} \right|}}{{{T_n}}} \cdot \sum\limits_{i = 1}^M {\exp \left[{\rm j}2{π} {{f \!_i}(d - △)} \right]} \end{aligned} $ | (9) |
| $\begin{aligned} F(△\left| d \right.) = & \frac{{{T_n} - \left| {(d - △)} \right|}}{{{T_n}}} \cdot \exp \left[{{\rm{j}}2{π} \bar f(d - △)} \right] \\ & \cdot \sum\limits_{i = 1}^M {\exp \left[{{\rm{j}}2{π} ({f \!_i} - \bar f)(d - △)} \right]} \end{aligned}$ | (10) |
$\bar f$为各段载频均值,对$F(△\left| d \right.)$取绝对值即可将难以运算操作的复数项$\exp \left[{{\rm{j}}2{π} \bar f(d - △)} \right]$简化为1,利用=欧拉公式,将式(10)中剩余复数项$\sum\nolimits_{i = 1}^M {\exp \left[{{\rm{j}}2{π} ({f \!_i} - \bar f)} \right.} $ $\left. \cdot {(d - △)} \right]$展开得到:
| $ \begin{aligned} & \sum\limits_{i = 1}^M {\exp \left[{{\rm{j}}2{π} ({f\!_i} - \bar f)(d - △)} \right]} \\ & \quad\quad = \sum\limits_{i = 1}^M {\cos \left[{2{π} ({f\!_i} - \bar f)(d - △)} \right]} \\ & \quad\quad\quad + \sum\limits_{i = 1}^M {{\rm{j}}\sin \left[{2{π} ({f \!_i} - \bar f)(d - △)} \right]} \end{aligned} $ | (11) |
利用上文介绍的FSK-BPSK信号频率分布的一般性特点,子脉冲载频fi在$\bar f$附近对称分布,但并不需要载频满足单调递增递减分布。换句话说,假设子脉冲中存在载频值为$\bar f +F $的子脉冲,就必然存在载频值为$\bar f -F $的子脉冲,F为子脉冲载频差分值。由于式(11)中的信号虚部${\rm{j}}\sin \left[{2{π} ({f \!_i} - \bar f)(d - △)} \right]$是奇函数,而复数项$\sum\nolimits_{i = 1}^M {\exp \left[{{\rm{j}}2{π} ({f \!_i} - \bar f)(d - △)} \right]} $中恰好存在互为相反数的奇函数,因此复数项的虚部${\rm{j}}\sin \left[{2{π} ({f \!_i} - \bar f)(d - △)} \right]$可通过自身正负项的相互抵消而完全被消除,使得信号可以只保留便于计算操作的信号实部信息$\cos \left[{2{π} ({f \!_i} - \bar f)(d - △)} \right]$。
当子脉冲个数为偶数时,式(11)可直接写成式(12):
| $ \begin{aligned} & \sum\limits_{i = 1}^M {\exp \left[{{\rm{j}}2{π} ({f \!_i} - \bar f)(d - △)} \right]} \\ & \quad\quad = \sum\limits_{i = 1}^M {\cos \left[{2{π} ({f \!_i} - \bar f)(d - △)} \right]} \end{aligned} $ | (12) |
当子脉冲个数为奇数时,式(11)可直接写成式(13):
| $ \begin{aligned} & \sum\limits_{i = 1}^M {\exp \left[{{\rm{j}}2{π} ({f \!_i} - \bar f)(d - △)} \right]} \\ & \quad\quad = \sum\limits_{i = 1}^{(M - 1)/2} {\cos \left[{2{π} ({f \!_i} - \bar f)(d - △)} \right]} + 1 \\ & \quad\quad\quad \ + \sum\limits_{i = (M + 1)/2}^M {\cos \left[{2{π} ({f \!_i} - \bar f)(d - △)} \right]} \end{aligned} $ | (13) |
从式(12) 、式(13)可以看出,子脉冲个数无论为奇数或偶数,本质上并不影响函数结果,完全可以统一用式(12)表示。将式(12)代入式(10)可得相关函数结果:
| $ \begin{aligned} \left| {F(△\left| d \right.)} \right| = & \left| {\frac{{{T_n} - \left| {d - △} \right|}}{{{T_n}}}} \right| \cdot 1 \\ & \cdot \left| {\sum\limits_{i = 1}^M {\cos \left[{2{π} ({f \!_i} - \bar f)(d - △)} \right]} } \right| \end{aligned} $ | (14) |
在上一节中提到相关函数表达式(14)中的d,其实就是式(4)中时差值t在时域区间[-T,+T]内按照采样间隔$△T \;$提取的时延量样值,所有样值d放在一起可组成一个向量${{D} ^\prime} = {[{d_1} \ {d_2} \ \cdots \ {d_{i - 1}} \ {d_i}]^{\rm{H}}}$。式(14)的向量形式F为:
| $ \begin{aligned} {F} = & \left| {F(△\left| {{{D}^\prime}} \right.)} \right| = [F(△\left| {{d_1}} \right.)\,\ F(△\left| {{d_2}} \right.)\ \,\cdots \\ & \quad F(△\left| {{d_{i - 1}}} \right.)\,\ F(△\left| {{d_i}} \right.)] \end{aligned} $ | (15) |
时差值$△$每一次搜索代入式(15)计算都对应一个相关函数结果曲线,曲线向量表示形式为S2。时差值$△$的遍历区间可根据系统基线距离适当选择[12]。
相关函数结果曲线S2相比于信号相关特性曲线S1的主要差异为结果曲线表达式中变量不同。在基本相关法中是时差值D未知,相关函数结果需要依靠时差值t的数字离散采样值依次代入式(4)遍历计算得到相关特性曲线,曲线的最大值处对应的时差值t即为时差估计值$\hat \tau $,可认为基本相关法中系统采样率决定了时差估计分辨率。而相关函数结果曲线S2的变量是时差值$△$本身,${{D}^\prime} = {[{d_1}\ {d_2} \ \cdots \ {d_{i - 1}} \ {d_i}]^{\rm{H}}}$是确定量,它是用时差值$△$一维搜索真实时差值,当时差值$△$搜索到恰好为真实时差值D时,相关函数结果曲线S2与信号相关特性曲线S1的欧氏距离最小,从而得到时差估计值$\widehat △$。
因此,本文提出一种相关函数拟合算法来计算曲线S1,S2距离。拟合函数$J(\theta ,△)$是一个关于幅度改善因子q和时差值$△$的函数。这是因为在计算信号的相关特性曲线中利用了FSK-BPSK复合调制信号的幅度信息[13],而在本文提出的时差估计方法中,为了便于相关函数的计算,默认信号脉冲幅度A=1,因此拟合函数$J(\theta ,△)$中存在一个幅度改善因子q,$J(\theta ,△)$可表示为:
| $ J(\theta ,△) = {(\theta \cdot {{S}_2} - {{S}_1})^{\rm{H}}}(\theta \cdot {{S}_2} - {{S}_1}) $ | (16) |
| $ \theta = \mathop {\arg \min }\limits_\theta [\,{(\theta \cdot {{S}_2} - {{S}_1})^{\rm{H}}}(\theta \cdot {{S}_2} - {{S}_1})] $ | (17) |
$J(\theta ,△)$其梯度为:
| $ \frac{{\partial J(\theta ,△)}}{{\partial \theta }} = 2 \cdot \theta \cdot {{S}_2^{\rm{H}}} \cdot {{S}_2} - \,2 \cdot {{S}_1^{\rm{H}}} \cdot {{S}_2} $ | (18) |
令式(18)梯度等于零,得参数q的估计量$ \hat \theta $:
| $ \hat \theta = {({{S}_2^{\rm{H}}} \cdot {{S}_2})^{ - 1}}({{S}_1^{\rm{H}}} \cdot {{S}_2}) $ | (19) |
求出参数$ \hat \theta $后,将$ \hat \theta $反代入函数式$J(\theta ,△)$求得最小距离Jmin:
| $ {J_{\min }} = {(\hat \theta \cdot {{S}_2} - {{S}_1})^{\rm{H}}} \cdot (\hat \theta \cdot {{S}_2} - {{S}_1}) $ | (20) |
为了验证本文针对FSK-BPSK复合调制信号所提时差估计算法的有效性,并且与基本相关法时差估计性能相比较,下面进行计算机仿真实验。
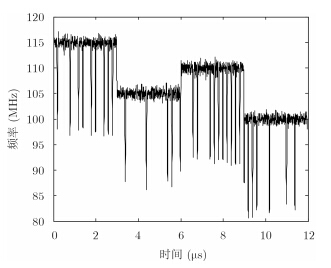
4.1 算法结果实验中仿真的FSK-BPSK复合调制信号为4段子脉冲组合而成,4段子脉冲载频fi分别为115 MHz,105 MHz,110 MHz,100 MHz,每段子脉冲时宽Tm为3 µs,子脉冲带宽B为5 MHz,码元时宽Tn为Tn=1/Bw=0.2 µs,采样频率fs为500 MHz。仿真环境信噪比设置为10 dB,两路信号时差D设置为1 ns。为了不失一般性,相位编码信号的相位改变完全随机产生。图 2为仿真FSK-BPSK复合调制信号的瞬时频率(Instantaneous Frequency,IF)图。从图 2可看出在码元相位变化处存在明显的频率跳变。
|
图 2 FSK-BPSK复合调制信号瞬时频率图 Fig.2 The IF of FSK-BPSK hybrid modulation signal |
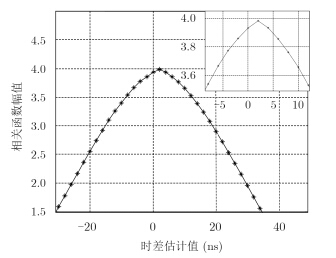
基本相关法中采样频率决定了时差估计分辨率,信号在500 MHz采样频率条件下时差估计只能达到${D} T = 1/{f_s} = 2\;{\rm{ns}}$的时域分辨率。伴随时差值t的遍历,两路信号互相关函数结果如图 3所示,图 3右上角为局部放大示意图。从局部放大图可以看出,当时差值t为2 ns时,相关函数取得最大值,即认为通过基本相关法得到的时差估计值$\hat \tau $为2 ns。
|
图 3 互相关函数 Fig.3 Cross correlation function |
为了尽可能避免基本相关法的时差估计精度较低、误差较大等问题,可在时差估计值的小范围内采用插值算法进行进一步精确估计。本文对此方法也进行了仿真验证。
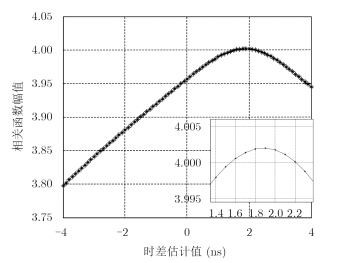
图 4为小范围时域区间内采用插值函数结果示意图。图 4右下角为局部放大的插值示意图。从局部放大图中可看出,插值函数的时域插值区间从-4 ns到4 ns,插值间距为0.1 ns,采用插值方法得到的时差估计值$\hat \tau $为1.9 ns,相比于基本相关法准确性有了微小改善,但由于插值函数的插值规则与相关函数有所差异,加上环境噪声的影响,时差估计准确性还有待提高。
|
图 4 插值函数 Fig.4 Interpolation function |
下面采用本文提出的相关函数拟合算法对该信号进行时差估计仿真实验。
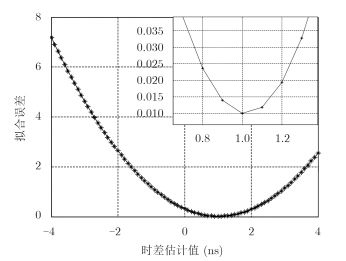
图 5为拟合函数$J$($\theta$ ,△)随着时差值△的遍历而得到的结果示意图,图 5右上角为$J$($\theta$ ,△)局部放大示意图。从放大图中可以明显看出,当时差值△为1 ns时,拟合函数$J$($\theta$ ,△)取得最小值Jmin。实验表明,本文提出的相关函数拟合算法得到的时差估计值与文中假设的时差值一致,相比于信号相关特性函数与插值函数等方法的准确性有明显提高。
|
图 5 拟合误差结果图 Fig.5 The result of fitting error |
在时差值D设置为1 ns情况下,利用插值方法和相关函数拟合算法针对上述FSK-BPSK复合调制信号在不同条件下进行时差估计,比较两种算法估计结果。
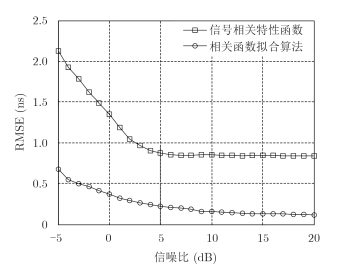
4.2.1 对信噪比的适应性在子脉冲带宽B恒定设置为5 MHz情况下,通过次数为5000次的蒙特卡洛仿真实验,比较两种方法在不同SNR条件下的估计误差,结果如图 6所示。
|
图 6 两种算法对信噪比的适应性 Fig.6 The adaptability of SNR |
由图 6可知,在FSK-BPSK复合调制信号时延估计中,插值算法的时延估计均方根误差(RMSE)大于相关函数拟合算法,随着SNR的增大,插值算法的RMSE迅速减小,相关函数拟合算法的RMSE逐渐减小。说明在相同的参数设置条件下,本文提出的针对FSK-BPSK复合调制信号的时差估计算法尤其适合在低SNR条件下需要得到高精度时延估计量的情况。
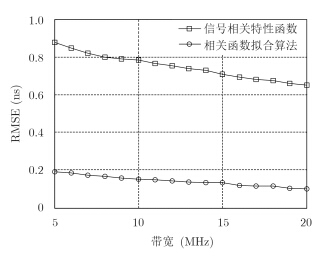
4.2.2 对带宽的适应性在SNR恒定设置为15 dB情况下,通过次数为5000次的蒙特卡洛仿真实验,比较两种方法在子脉冲带宽不同的条件下的估计误差,结果如图 7所示。
|
图 7 两种算法对带宽的适应性 Fig.7 The adaptability of bandwidth |
由图 7可知,信号相关特性函数对于带宽敏感,随着带宽增大导致明显的估计误差减小。说明基本相关法在做时差估计时更适合带宽较大信号。而相关函数拟合算法随着带宽的增大,时差估计的RMSE仅仅只有缓慢的下降趋势,说明本文提出的相关函数拟合算法对于FSK-BPSK复合调制信号的带宽并不敏感,相比于基本相关法,当复合调制信号带宽较小时,相关函数拟合算法的时差估计精度更高。
5 结论
本文针对现代复杂雷达环境中一种常用特殊信号——FSK-BPSK复合调制信号,提出了一种新的时差估计算法。该算法根据信号的相关特性,通过子脉冲相关函数的理论推导得出FSK-BPSK复合调制信号相关函数。同时有效地结合了FSK-BPSK复合调制信号自身的频率对称分布特点和子脉冲时宽相同等特点,可将FSK-BPSK复合调制信号相关函数中复杂的信号虚部予以消除,保留信号实部信息。伴随时差值在一定时域区间的1维搜索可得到一系列近似信号相关特性函数结果曲线,将得到的时差估计结果曲线拟合信号相关特性曲线,当两条曲线拟合误差达到最小时即可反推出精确时差估计值。仿真实验表明,该方法能够精确地估计信号时间延迟,在SNR较低情况下,估计精度较高,估计误差相对于基本相关算法有明显改善,同时该算法对于复合调制信号的带宽不敏感,尤其适合小带宽复合调制信号的时差估计情况。
| [1] | 郭福成, 樊昀, 周一宇, 等. 空间电子侦察定位原理[M]. 北京: 国防工业出版社, 2012: 57, 81. Guo Fu-cheng, Fan Yun, Zhou Yi-yu, et al.. Localization Principles in Space Electronic Reconnaissance[M]. Beijing: National Defense Industry Press, 2012: 57, 81.(  1) 1) |
| [2] | 孙仲康, 周一宇, 何黎星. 单多基地有源无源定位技术[M]. 北京: 国防工业出版社, 1996: 21-26. Sun Zhong-kang, Zhou Yi-yu, and He Li-xing. Location Technology for Single/Multiple Base with Active and Passive Sensors[M]. Beijing: National Defense Industry Press, 1996: 21-26.(  1) 1) |
| [3] | 宋军, 刘渝, 王旭东. FSK/BPSK复合调制信号识别与参数估计[J]. 电子与信息学报, 2013, 35(12): 2868-2873. Song Jun, Liu Yu, and Wang Xu-dong. The recognition and parameter estimation of hybrid modulation signal combined with FSK and BPSK[J]. Journal of Electronics & Information Technology, 2013, 35(12): 2868-2873.(  2) 2) |
| [4] | 胡泽宾, 赵惠昌, 孙巍. 伪码调相与正弦调幅复合调制引信[J]. 电子与信息学报, 2005, 27(8): 1237-1239. Hu Ze-bin, Zhao Hui-chang, and Sun Wei. Pseudo-random code phase-modulation and sine amplitude-modulation combined modulated fuze[J]. Journal of Electronics & Information Technology, 2005, 27(8): 1237-1239.(  1) 1) |
| [5] | 张小飞, 汪飞, 徐大专. 阵列信号处理的理论和应用[M]. 北京: 国防工业出版社, 2010: 158-161. Zhang Xiao-fei, Wang Fei, and Xu Da-zhuan. The Thesis and Application of Array Signal Processing[M]. Beijing: National Defence Industry Press, 2010: 158-161.(  1) 1) |
| [6] | Ahmed Masmoudi, Faouzi Bellili, and Sofiene Affes. A non-data-aided maximum likehood time delay estimator using importance sampling[J]. IEEE Transactions on Signal Processing, 2011, 59(10): 4505-4514.( 1) 1) |
| [7] | 李晶. 基于角度和时延估计的单站多外辐射源定位跟踪方法研究[D]. [硕士论文], 信息工程大学, 2014: 27. Li Jing. Research on single-observer multiple-emitter passive coherent location and tracking based on angle and time delay estimation[D]. [Master dissertation], Information Engineering University, 2014: 27.(  1) 1) |
| [8] | Ho K C, Lu Xiao-ning, and Kovavisarush L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684-696.( 1) 1) |
| [9] | Ge Feng-xiang, Shen Dong-xu, Peng Ying-ning, et al.. Super-resolution time delay estimation in multipath environments[J]. IEEE Transactions on Circuits and Systems I: Regular Paper, 2007, 54(9): 1977-1986.( 1) 1) |
| [10] | Shen Jun-yang, Molisch A F, and Salmi J. Accurate passive location estimation using TOA measurements[J]. IEEE Transactions on Wireless Communications, 2012, 11(6): 2182-2192.( 1) 1) |
| [11] | Ng W, Reilly J P, Kirubarajan T, et al.. Wideband array signal processing using MCMC methods[J]. IEEE Transactions on Signal Processing, 2013, 7(3): 532-542.( 1) 1) |
| [12] | 吴泽民, 任姝婕. 雷达时差和系统误差的联合估计方法[J]. 兵工学报, 2011, 32(7): 847-852. Wu Ze-min and Ren Shu-jie. Joint estimation for time offset and radar system error[J]. Acta Armamentarii, 2011, 32(7): 847-852.(  1) 1) |
| [13] | 钟森, 夏威, 何子述. 相位噪声对时差估计的影响和分析[J]. 电子与信息学报, 2014, 36(11): 2614-2620. Zhong Sen, Xia Wei, and He Zi-shu. Analysis of the effect of phase noise on time difference estimation[J]. Journal of Electronics & Information Technology, 2014, 36(11): 2614-2620.(  1) 1) |


