随着现代雷达等探测设备分辨率的不断提高,目标的回波信号可能分布在不同的距离分辨单元中,其探测场不再等效为一个点,即单个目标可能同时产生多个量测,称这样的目标为扩展目标[1, 2]。目前,扩展目标跟踪已成为跟踪领域中研究的一个热点问题,尤其是对杂波环境下多扩展目标跟踪(Extended Targets Tracking, ETT)算法的研究和应用,已受到国内外学者的广泛关注[3, 4, 5]。针对杂波环境下扩展目标跟踪问题,不仅要排除杂波的干扰,还要解决多个量测对应同一个目标的问题,对跟踪技术提出了更高的要求。
杂波环境下多扩展目标跟踪中,由于存在多个量测对应一个目标的问题,传统的点目标跟踪中量测与目标一一对应的假设条件不再成立,其数据关联过程将变得非常复杂。针对数目变化的点目标跟踪,Mahler于2003年提出了随机有限集 (Random Finite Set, RFS) 理论[6]及随后Vo等人[7]提出了多目标跟踪概率假设密度(Probability Hypothesis Density, PHD)滤波算法,为杂波环境下数目变化的多目标跟踪问题提供了一种新的处理方法。2009年Mahler首次将PHD方法推广到多扩展目标跟踪领域中,给出了扩展目标PHD滤波的迭代更新公式[1]。随后,Granström等人在此基础上,将高斯混合技术应用到扩展目标PHD算法中,给出了算法的闭合解,形成了扩展目标高斯混合概率假设密度滤波算法(ET-GM-PHD)[8]。文献[9]中进一步提出了基于势概率假设密度的多扩展目标跟踪算法(ET-CPHD)。
多扩展目标跟踪中首要解决的关键问题之一是对量测集的划分问题,因为在多扩展目标跟踪中,多个量测对应同一个目标,但传感器无法判断量测是否来源于同一个目标,也无法直接给出量测子集与目标之间的对应关系。文献[8, 10]中提出采用距离划分量测集,但由于扩展目标形状不确定,且跟踪场景中存在大量杂波的干扰,很难对量测集进行准确的划分,直接影响后续的多扩展目标跟踪性能。此外,该方法采用距离集遍历划分,具有较高的时间计算复杂度,影响算法的实时性。文献[8]同时给出了K-means++方法,由于该算法中对K的取值问题没有加以讨论,如果初始的K取值不合理将直接影响量测集的划分效果。文献[11]中针对紧邻的多扩展目标量测集划分问题提出了预测划分方法和期望最大划分方法,其中,预测划分方法是基于分量预测信息进行量测集划分,该方法划分的准确度主要依赖于扩展目标的预测状态和形状参数,仅当扩展目标的前一帧状态和形状估计准确,且预测也准确时,才能较准确地划分量测集;如果扩展目标发生转弯机动或其他机动导致预测不准时,该方法失效。期望最大划分方法同样对发生机动的扩展目标性能下降,且容易收敛到局部最大和出现奇异解等问题。文献[12]中将谱聚类技术引入到量测集划分问题中,针对不同的量测集划分取得了一定划分效果,但在算法中进行谱聚类的时候,同样要对K值的选取进行讨论。
针对上述量测集划分中存在的问题,本文将近邻传播聚类技术引入到量测集划分中,提出一种新的快速多扩展目标量测集划分算法。该算法首先计算每个量测点的邻域高斯核函数之和,将其用来估计量测点的密度,并选取合适密度阈值去除杂波量测;然后根据近邻传播算法提取目标的质心,进而获得量测集的聚类结果,最后通过扩展目标PHD滤波算法,实现对扩展目标的目标数目估计和状态提取。 2 量测集划分问题描述
在多扩展目标跟踪中,由于单个扩展目标可产生多个量测,需要对量测集进行划分,尽可能让同一目标产生的量测属于同一类。为了方便描述问题,假定k时刻,传感器探测到3个量测,表示为${Z_k} = \left\{ {z_k^{(1)},z_k^{(2)},z_k^{(3)}} \right\}$,则量测集可能有以下5种不同的划分方式:
| $\eqalign{ & {P_{\rm{1}}}{\rm{ : }}{W_{\rm{1}}}^1 = \left\{ {{{\rm{z}}_k}^{(1)},{{\rm{z}}_k}^{(2)},{{\rm{z}}_k}^{(3)},} \right\} \cr & {\rm{ }}{P_{\rm{2}}}{\rm{ : }}{W_{\rm{1}}}^2{\rm{ = }}\left\{ {{{\rm{z}}_k}^{(1)},{{\rm{z}}_k}^{(2)}} \right\}{\rm{,}}{W_{\rm{2}}}^2 = \left\{ {{{\rm{z}}_k}^{(3)}} \right\} \cr & {P_{\rm{3}}}{\rm{ : }}{W_{\rm{1}}}^3 = \left\{ {{{\rm{z}}_k}^{(1)},{{\rm{z}}_k}^{(3)}} \right\}{\rm{,}}{W_{\rm{2}}}^3 = \left\{ {{{\rm{z}}_k}^{(2)}} \right\} \cr & {P_{\rm{4}}}{\rm{ : }}{W_{\rm{1}}}^4 = \left\{ {{{\rm{z}}_k}^{(2)},{{\rm{z}}_k}^{(3)}} \right\}{\rm{,}}{W_{\rm{2}}}^4 = \left\{ {{{\rm{z}}_k}^{(1)}} \right\} \cr & {P_{\rm{5}}}{\rm{ : }}{W_{\rm{1}}}^5 = \left\{ {{{\rm{z}}_k}^{(1)}} \right\}{\rm{,}}{W_{\rm{2}}}^5 = \left\{ {{{\rm{z}}_k}^{(2)}} \right\},{W_{\rm{3}}}^5 = \left\{ {{{\rm{z}}_k}^{(3)}} \right\} \cr} $ |
由于复杂场景中包含大量的杂波干扰,影响量测集的划分速度和精度,本文将引入量测密度技术进行量测杂波预处理,然后采用近邻传播聚类方法实现对量测集划分,最后采用GM-PHD滤波算法进行目标数目估计和状态提取。 3.1 量测密度
设样本数据${x_1},{x_2}, \cdot \cdot \cdot ,{x_n} \subset {R^l}$为独立同分布的随机变量,且变量服从的分布密度函数假设为$f{\rm{(}}x{\rm{)}}$,则函数$f{\rm{(}}x{\rm{)}}$的核估计可表示为[13, 14]:
| $\hat f{\rm{(}}x{\rm{) = }}{1 \over {n{h^d}}}\sum\limits_{i = 1}^N K \left( {{{{x_i} - x} \over h}} \right)$ | (1) |
由式(1)可知,核密度估计$\hat f{\rm{(}}x{\rm{)}}$不仅与给定的样本点集合有关,还与核函数的选择和窗宽参数的选择有关。理论上,任何函数都可作为核函数,但为了方便密度函数估计,通常要求核函数满足以下条件:
(1)对称性:$K\left( { - u} \right) = K\left( u \right)$;
(2)有限性:${\rm{Sup|}}K\left( u \right){\rm{| < }}\infty ,\int {_{ - \infty }^{ + \infty }} K\left( u \right){\rm d}u = 1$。
满足以上条件的核函数有高斯核函数、Epanechnikov函数、Biweight核函数,本文选取高斯核函数,则密度函数可表示为:
| $\eqalign{ & f_{_{{\rm{Gauss}}}}^{\rm{D}}{\rm{ \ \ (}}x{\rm{) = }}{1 \over {n{h^{d{\rm{/2}}}}{{{\rm{(2}} {\rm \pi} {\rm{)}}}^{d{\rm{/2}}}}}} \cr & \qquad \qquad \cdot \sum\limits_{i = 1}^n {\exp } \left( { - {1 \over {2h}}\left( {x - {x_i}} \right){{\left( {x - {x_i}} \right)}^T}} \right) \cr} $ | (2) |
为了提高计算速度,仅考虑近邻点对其影响,因为距离较远的点对其产生的影响比较小,可以忽略不计,故近似密度函数可表示为:
| $f_{_{{\rm{Gauss}}}}^{\rm{D}}{\rm{ \ \ (}}x{\rm{) = }}{1 \over C}\sum\limits_{{x_i} \in near\left( x \right)} {\exp } \left( { - {{d{{\left( {x,{x_i}} \right)}^2}} \over {2h}}} \right)$ | (3) |
(1)根据式(3),可计算出量测集中每个量测点$z$的近似密度函数$f_{_{{\rm{Gauss}}}}^{\rm{D}}{\rm{ \ \ (}}z{\rm{)}}$,在不影响滤波结果的情况下,为降低计算量,本文选用经验值4-邻域估计量测点的密度。
(2)去除杂波量测。选取合适的密度阈值γ,如果$f_{_{{\rm{Gauss}}}}^{\rm{D}}{\rm{ \ \ (}}z{\rm{) < }}\tau $,设定$z$为杂波量测,并将其从量测集中删除,否则,认为$z$为由目标产生的量测。其中,t的取值可采用如下方法,先分别找出量测的缩小最大密度${f_{\max }}$和最小密度${f_{\min }}$;将密度区间$\left[ {{f_{\max }}{f_{\min }}} \right]$分成$N_z$等份,$N_z$为量测数,统计每个等分区间内包含量测的个数,寻找含有最少量测(或不含量测)的密度区间,将该区间内的任意密度值作为密度阈值$\tau $。 3.3 近邻传播聚类算法
近邻传播(AffinityPropagation,AP)聚类是一种具有竞争力的无监督聚类算法,在相似度矩阵的基础上进行聚类,其目的是找到最优的类代表点集合,使得所有数据点到最近的类代表点的相似度之和最大,其中,类代表点为数据集中的某一个数据点。
本文选用欧式距离作为相似度的测度指标,即任意两点距离平方的负数作为两点之间的相似度。例如,点${x_i}$和点${x_j}$之间的相似度可表示为$s(i,j{\rm{) = - }}{\left\| {{x_i} - {x_j}} \right\|^2}$,表示数据点${x_i}$适合作为${x_j}$的类代表点的程度。由相似度构成的$n×n$的矩阵称为相似度矩阵,表示为$S = {[{s_{i,k}}]_{n \times n}}$。在AP算法聚类之前,为每个数据点$xi$设定偏向参数$s(i,i)$。若$s(i,i)$的值越大,则数据点$xi$作为类代表点的可能性越大。算法初始化时,假设所有的数据点作为类代表点的概率相同,即$s(i,i)=p,i=1,2,···,n$,其中$n$为数据点数,$p$值的大小将直接影响到最终得到类的个数,AP聚类算法就是通过调节p值达到寻找合适的聚类数目。通常情况下,$p$值越大,类别数越多[15]。
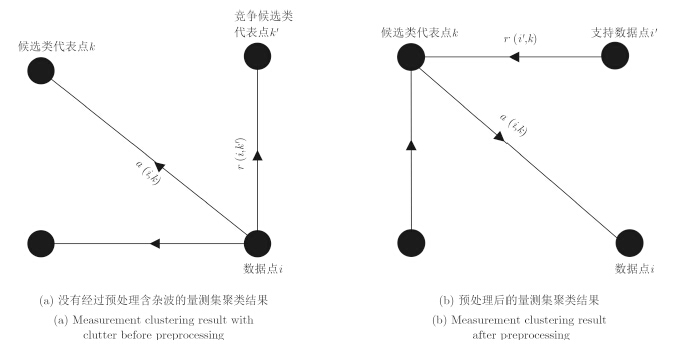
AP算法中包含两个重要的信息参数,即吸引度$r(i,k)$和归属度$a(i,k)$。算法迭代过程中两个数据信息迭代更新,两个参数从不同角度考虑竞争的目的,其中$r(i,k)$是从数据点xi指向候选类代表点$xk$,表示$xk$合适作为点xi的类代表点的代表程度,反映点xk的积累证据,如图 1(a)所示。$a(i,k)$是从候选类代表点xk指向数据点$xi$,表示点$xi$选择$xk$作为类代表的合适程度,反映点$xk$的积累证据,如图 1(b)所示。AP确定类代表点的过程实质是不断更新迭代每个点信息参数$r(i,k)$和$a(i,k)$的值,$r(i,k)$与$a(i,k)$的值越大,则k点作为聚类中心的可能性就越大。
|
图 1 数据点与候选类代表点之间关系图 Fig.1 The relation of the data point i and the candidate exemplar k |
$r(i,k)$和$a(i,k)$的迭代更新过程为:
| $r{\rm{(}}i,k{\rm{) }} \leftarrow s{\rm{(}}i, k{\rm{) - }}\mathop {{\rm{max}}}\limits_{k' \ne k} \left\{ {a{\rm{(}}i, k'{\rm{) + }}s{\rm{(}}i, k'{\rm{)}}} \right\}$ | (4) |
| $a{\rm{(}}i, k{\rm{)}} \leftarrow \min \left\{ {0,r{\rm{(}}k, k{\rm{) + }}\sum\limits_{i' \ne i,i' \ne k} {{\rm{max}}\left\{ {0,r{\rm{(}}i', k{\rm{)}}} \right\}} } \right\}$ | (5) |
| $a{\rm{(}}k, k{\rm{)}} \leftarrow \sum\limits_{i' \ne k} {{\rm{max}}\left\{ {0,r{\rm{(}}i', k{\rm{)}}} \right\}} $ | (6) |
为避免聚类结果发生震荡,文献[15]中引入了一个阻尼参数l,在每次信息迭代更新中,$r(i,k)$和$a(i,k)$的更新结果由当前迭代过程中更新的值和上一次迭代的结果加权得到,迭代公式为[15]:
| ${r^{\left( j \right)}}{\rm{(}}i,k{\rm{) = }}\left( {1 - \lambda } \right) \cdot \left\{ {s{\rm{(}}i, k{\rm{)}} - \mathop {{\rm{max}}}\limits_{k' \ne k} \left\{ {a{\rm{(}}i, k'{\rm{) \\ \qquad \qquad \ + }}s{\rm{(}}i, k'{\rm{)}}} \right\}} \right\} + \lambda \cdot {r^{j - 1}}{\rm{(}}i, k{\rm{)}}$ | (7) |
| ${a^j}(i,k){\rm{ = }}\left( {1 - \lambda } \right) \cdot \left( {\min \left\{ {0,r(k,k) \\ \qquad \qquad {\rm{ + }}\sum\limits_{i' \ne i,i' \ne k} {{\rm{max}}\left\{ {0,r(i',k)} \right\}} } \right\}} \right) \\ \qquad \qquad + \lambda \cdot {a^{j - 1}}{\rm{(}}i,k{\rm{)}}, \quad i \ne k$ | (8) |
| ${a^j}{\rm{(}}i,k{\rm{) = }}\left( {1 - \lambda } \right) \cdot \left( {\sum\limits_{i' \ne k} {{\rm{max}}\left\{ {0,r{\rm{(}}i', k{\rm{)}}} \right\}} } \right) \\ \qquad \qquad + \lambda \cdot {a^{j - 1}}{\rm{(}}i,k{\rm{)}}$ | (9) |
AP算法的基本步骤为:
(1)初始化,计算相似度矩阵$S = {[{s_{i,k}}]_{n \times n}}$,$n$为数据点数,信息参数${a^{(0)}}(i,k) = {r^{(0)}}(i,k) = 0$;相似度矩阵对角线元素$s(k,k)=p$,其中,$p$取数据集相似度矩阵非对角元素的均值;
(2)根据式(7)-式(9),更新参数值$a(i,k)$和$r(i,k)$;
(3)计算每个数据点的类代表点。点$x_i$的类代表点为$(a(i,k)+r(i,k))$最大值所对应的点;
(4)如果迭代次数超过设定最大数目,或者聚类中心变化小于阈值$\theta $,则终止迭代,否则返回步骤(2)。
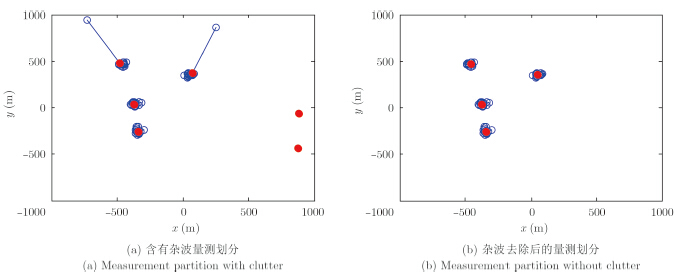
图 2为扩展目标跟踪场景中单帧量测数据聚类结果,其中,图 2(a)为没有经过预处理含杂波的量测集聚类结果,图 2(b)为预处理后的量测聚类结果。可以看出,杂波点对AP算法存在一定的干扰,经过量测杂波预处理,AP算法可以较好地划分扩展目标的量测数据,且聚类中心要略好于有杂波干扰的聚类结果。所以本文算法中,先对量测进行预处理,降低杂波对AP算法的干扰,以提高算法的跟踪性能。
|
图 2 量测集划分结果 Fig.2 Measurement partition |
本文将所提算法与传统的距离划分[8]和K-means++划分[8]作性能对比分析,其中,3种算法都在扩展目标高斯混合PHD(ET-GMPHD)的滤波框架[8]下实现。采用OSPA距离作为多扩展目标跟踪精度的评价指标之一,其定义如下[16]:
| $\eqalign{ & \bar d_p^{(c)}{\rm{(}}X,Z{\rm{)}} \cr & {\rm{ = }}{\left( {{1 \over n}\left( {\mathop {{\rm{min}}}\limits_{\pi \in {\prod _n}} \sum\limits_{i = 1}^{ m} {d_{}^{(c)}} {{\left( {{x_i},{z_{\pi \left( i \right)}}} \right)}^p} + {c^p}\left( {n - m} \right)} \right)} \right)^{1/p}} \cr} $ | (10) |
假设$k$时刻每个扩展目标状态表示为${X_k} = [{x_k},{y_k},{v_x}_,{_k},{v_y}_,{_k}]^\rm T$,其中$(x_k,y_k)$表示位置,$(v_x,k,v_y,k)$表示速度。传感器量测表示为$z_k^{(j)} = \left[ {x_k^{(j)},y_k^{(j)}} \right]$,目标状态转移矩阵$F = \left[ \matrix{ {I_2} \ \Delta t{I_2} \hfill \cr {0_2} \ \ \ {I_2} \hfill \cr} \right]$,过程噪声协方差矩阵
| $$Q = \sigma _v^2\left[ \matrix{ {{\Delta {t^4}} \over 4}{I_2} \ \ {{\Delta {t^3}} \over 4}{I_2} \hfill \cr {{\Delta {t^3}} \over 2}{I_2} \ \ \Delta {t^2}{I_2} \hfill \cr} \right]$$ |
实验1 交叉目标跟踪场景
假设新生目标随机集的强度函数为: ${D_b}(x) \!\! =\!\! 0.1N\left( {x ;m_{_b}^{(1)},{P_b}} \right) + 0.1N\left( {x ;m_{_b}^{(2)},{P_b}} \right) \!\!+\!\! 0.1N\left( {x ;m_{_b}^{(3)},{P_b}} \right) \!\!+ 0.1N\left( {x ;m_{_b}^{(4)},{P_b}} \right)$。其中,$m_{_b}^{(1)}{\rm{ = }}{\left[ { - 800 - 600 \;\; 0 \;\; 0} \right]^\rm T},m_{_b}^{(2)}{\rm{ = }}{\left[ { - 900 \;\; 100 \;\; 0 \;\; 0} \right]^\rm T},m_{_b}^{(3)}{\rm{ = }}{\left[ { - 700 \;\; 700 \;\; 0 \;\; 0} \right]^\rm T},$ $m_{_b}^{(4)}{\rm{ = }}{\left[ { - 100 \;\; 700 \;\; 0 \;\; 0} \right]^\rm T},{P_b} = \rm{diag}\left( {\left[ {100 \;\; 100 \;\; 25 \;\; 25} \right]} \right)$。
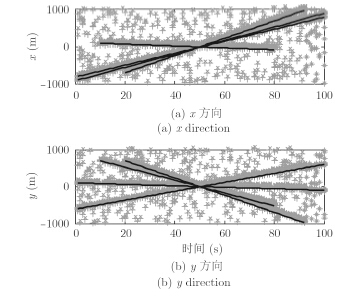
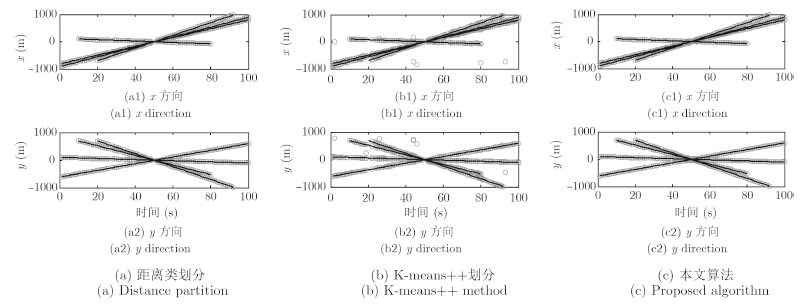
图 3为扩展目标分别在x和y方向上的真实运动轨迹和量测。图 4(a),图 4(b),图 4(c)分别表示距离划分、K-means++划分和AP聚类划分的目标状态估计。从图中可以明显看出,本文算法与距离划分算法的多扩展目标跟踪精度相当,而K-means++方法划分的跟踪精度最差,主要是因为K-means++方法对初始聚类中心的要求比较高,且对杂波比较敏感,导致量测划分不准确,影响滤波结果。
|
图 3 扩展目标真实轨迹及量测 Fig.3 Real tracks of the extended targets and measurements |
|
图 4 目标状态估计 Fig.4 State estimates of the targets |
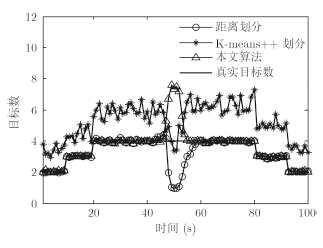
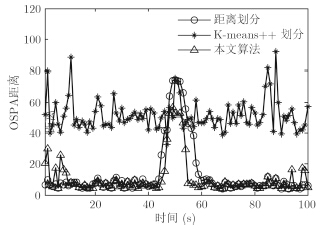
第50时刻,由于扩展目标交叉,量测集部分重叠在一起,导致量测很难被准确划分。由图 5可以看出,在第50s时,3种算法对目标数的估计都不准确。图 6给出了3种算法的OSPA距离比较,可以看出,本文算法与距离划分算法的精度相当,都明显好于K-means++算法。
|
图 5 目标数估计 Fig.5 Number estimates of the targets |
|
图 6 OSPA距离 Fig.6 OSPA distance |
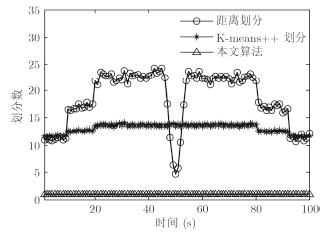
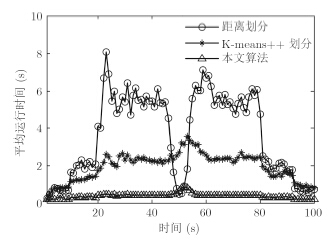
图 7和图 8表示量测的划分数和算法的平均运行时间。可以看出,由于距离划分算法中,事先根据经验设定距离子集,并遍历距离集划分量测,导致量测划分数最大,从而导致该算法整体运行时间最长;而对K-means++划分,很难确定K的取值范围,导致量测划分数也比较多;本文算法的量测划分数最小,因为本文算法中首先采用量测密度技术滤除了杂波点,并在AP聚类选用自适应P值进行聚类,大大减少了量测集的划分数目,在不降低滤波精度的情况下,大大缩短了算法的运行时间。
|
图 7 划分数估计 Fig.7 Partition number estimates |
|
图 8 平均运行时间 Fig.8 Average run-time |
实验2 紧邻扩展目标跟踪场景
假设跟踪场景中含有两个扩展目标,且两目标同时在第一时刻出现,最后时刻消失,在此过程中两目标同向且相距100m。设新生目标随机集的强度函数为: ${D_b}(x ) = 0.1N\left( {x ;m_{_b}^{(1)},{P_b}} \right) + 0.1N\left( {x ;m_{_b}^{(2)},{P_b}} \right)$ 其中,mb(1)=[-800-600 0 0]T,mb(2)=[-700-500 0 0]T,Pb=diag([100 100 25 25]),其他参数同实验1。
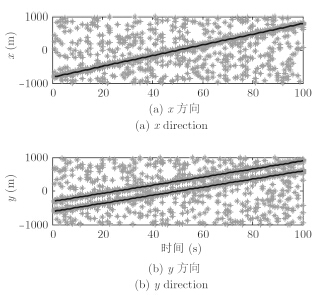
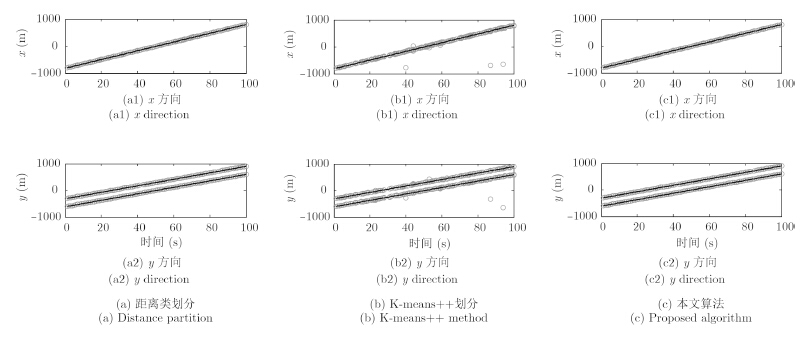
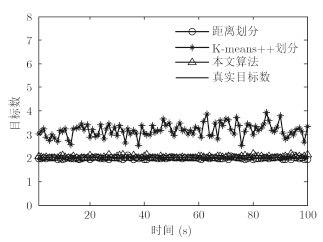
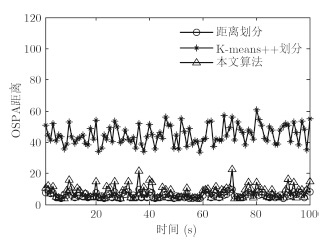
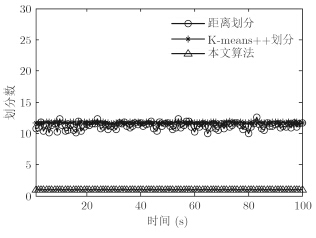
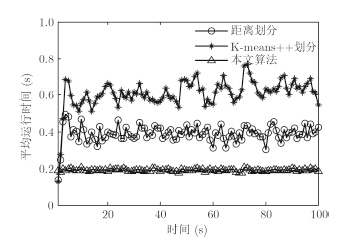
图 9给出量测及目标在x轴和y轴上的运动轨迹,图 10(a),图 10(b),图 10(c)分别为距离划分、K-means++划分和本文算法的目标状态估计。图 11和图 12分别给出了采用3种算法对目标数的估计和OSPA距离统计的对比图。图 13和图 14分别为3种算法的划分数和平均运行时间的对比图。从实验结果可以看出,本文算法与基于距离划分算法的精度相当,K-means++划分的跟踪效果最差。从运行时间上来说,提出算法的运行时间明显要低于其他两种算法,具有较好的实时性。
|
图 9 扩展目标真实轨迹及量测 Fig.9 Real tracks of the extended targets and measurements |
|
图 10 目标状态估计 Fig.10 State estimates of the targets |
|
图 11 目标数估计 Fig.11 Number estimates of the targets |
|
图 12 OSPA距离 Fig.12 OSPA distance |
|
图 13 划分数估计 Fig.13 Partition number estimates |
|
图 14 平均运行时间 Fig.14 Average run-time |
针对杂波环境下多扩展目标量测集难以划分,且时间代价高的问题,本文引入AP聚类技术,提出一种基于AP聚类的划分算法。首先,对每个量测点进行密度估计,采用密度分析技术去除杂波量测,然后运用AP聚类技术进行量测集划分。最后通过两组实验验证提出的算法在不影响滤波精度的情况下,可以大大减少量测集的划分数,降低滤波的计算代价,具有一定的实际工程应用价值。此外,针对扩展目标跟踪,单个点状态已经难以充分描述扩展目标,需要结合形状信息加以描述。如果形状估计不准确,将直接影响扩展目标状态估计的精度,从而影响后续扩展目标能否正确进行身份识别和航迹关联等。本文的后续工作拟在提出算法的基础上,结合高斯曲面特征矩阵技术[17],联合估计多扩展目标的形状,并将其用于指导航迹跟踪,实现扩展目标的连续跟踪。
| [1] | Mahler R. PHD filters for nonstandard targets, I: Extended targets[C]. Proceedings of the 12th International Conference on Information Fusion, Seattle, USA, 2009: 915-921.( 2) 2) |
| [2] | Gilholm K, Godsill S, Maskell S, et al.. Poisson models for extended target and group tracking[C]. Proceedings of Signal and Data Processing of Small Targets, California, USA: SPIE, 2005: 230-241.( 1) 1) |
| [3] | Salmond D J and Parr M C. Track maintenance using measurements of target extent[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(6): 389-395.( 1) 1) |
| [4] | Koch J W. Bayesian approach to extended object and cluster tracking using random matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059.( 1) 1) |
| [5] | Swain A and Clark D. The PHD filter for extended target tracking with estimable extent shape parameters of varying size[C]. Proceedings of the 15th International Conference on Information Fusion, Singapore, 2012: 1111-1118.( 1) 1) |
| [6] | Mahler R P S. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.( 1) 1) |
| [7] | Vo B N and Ma W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104.( 1) 1) |
| [8] | Granstrom K, Lundquist C, and Orguner O. Extended target tracking using a Gaussian-mixture PHD filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3268-3286.( 5) 5) |
| [9] | Orguner U, Lundquist C, and Granstrom K. Extended target tracking with a cardinalized probability hypothesis density filter[C]. Proceedings of the 14th International Conference on Information Fusion, Chicago, USA, 2011: 1-8.( 1) 1) |
| [10] | Granstrom K, Lundquist C, and Orguner O. A Guassisan mixture PHD filter for Extended target tracking[C]. Proceedings of the 13th International Conference on Information Fusion, Edinburgh, UK, 2010: 1-8.( 1) 1) |
| [11] | Granstrom K and Orguner U. A PHD filter for tracking multiple extended targets using random matrices[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5657-5671.( 1) 1) |
| [12] | Yang Jin-long, Liu Feng-mei, Ge Hong-wei, et al.. Multiple extended target tracking algorithm based on GM-PHD filter and spectral clustering [J]. EURASIP Journal on Advances in Signal Processing, 2014, 117: 1-8.( 1) 1) |
| [13] | Botev Z I, Grotowski J F, and Kroese D P. Kernel density estimation via diffusion[J]. The Annals of Statistics, 2010, 38(5): 2916-2957.( 1) 1) |
| [14] | Hall P and Wand M. On the accuracy of binned kernel density estimators[J]. Journal of Multivariate Analysis, 1994, 56(2): 165-184.( 1) 1) |
| [15] | Frey B J and Dueck D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976.( 3) 3) |
| [16] | Schuhmacher D, Vo B T, and Vo B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.( 1) 1) |
| [17] | 李鹏, 杨金龙, 葛洪伟. 基于高斯曲面特征矩阵的扩展目标形状估计[J]. 光电子·激光, 2014, 25(9): 1803-1811. Li Peng, Yang Jin-long, and Ge Hong-wei. Shape estimation of extended targets based on Gaussian surface feature matrix[J]. Journal of Optoelectronics · Laser, 2014, 25(9): 1803-1811.(  1) 1) |
 2015, Vol. 4 Issue (4): 452-459
2015, Vol. 4 Issue (4): 452-459
