② 解放军工程兵学院 徐州 221000
② Engineer Academy of People’s Liberation Army, Xuzhou 221000, China
探地雷达(GroundPenetratingRadar,GPR)作为一种较新的无损检测设备,能够利用被测区域地下物质的介电性、导磁性差异,根据接收电磁波的动力学和运动学特征,推断地下介质和目标的结构和分布特性,从而实现地下检测目标的成像和定位。它具有操作简单、工作方式灵活、探测精度高、探测效率高等特点。随着人类对客观世界认知需求的不断提高和雷达技术的不断发展,探地雷达已广泛应用于考古、矿产资源勘探、地质灾害勘查、岩土工程调查、工程质量检测、军事探测等众多领域[1]。
探地雷达是对地下媒质内部的目标进行探测,接收信号的一个重要特点是杂波多且能量较强,如有收发耦合波、地表直达波、地下媒质内部引起的背景杂波等;而地下目标反射回波较弱。因此,受杂波干扰严重。尤其对于浅层目标而言,目标回波与直达波到达时间相接近,目标回波往往淹没在直达波信号中,很不利于目标的检测与识别。所以杂波抑制是探地雷达数据预处理的关键技术,也是提高目标检测、识别、成像等性能的关键环节。
目前国内外学者针对探地雷达信号杂波抑制问题提出了许多方法。这些方法主要可分为4类:基于杂波模型的方法,子空间投影方法,系统辨识方法,变换域方法[2]。根据对杂波模型的不同描述,基于杂波模型的方法可分为参数化模型、半参数化和非参数化模型3种[2]。其中,参数化模型的参数直接用来描述每个探测点的杂波。VanderMerwe用衰减指数模型来描述地下介质不均匀特性导致的电磁波幅度和相位的变化,通过循环迭代的优化方法分离出地杂波和有用信号[3]。半参数化模型中的参数并不直接描述某探测点的杂波分布,而是描述不同探测点杂波分布的空间相关性。Brunzellt提出的随机起伏地表的杂波模型以及线性预测算法均为半参数化模型方法[4]。非参数化模型方法主要包括均值法[5]、中值滤波等。子空间投影法主要包括主成分分析(PCA)[6, 7]和独立成分分析(ICA)[8]以及相应的改进方法[9, 10]。系统辨识方法中每道A-scan都要辨识,而且要求杂波或参考杂波已知。变换域方法主要利用小波变换[11]或Curvelet变换[12]进行直达波滤除。主成分分析法是利用主成分的相关性来实现滤波;小波变换方法需选择分辨率足够高的2维连续有向小波,并采用合适的小波参数才能达到较好的直达波去除效果。实际情况中,由于发射信号达不到理想波形以及受传播媒质的色散特性等影响,主成分分析法与小波变换法都难以达到很好的滤波效果。本文提出基于小波变换与主成分分析的直达波自适应抑制方法。通过比较不同实验方法对实测数据的处理结果,验证了本文方法的有效性。 2 基于小波变换的主成分分析法
主成分分析方法,是一种建立在最小均方误差基础上的线性变换处理法。奇异值分解变换算法是主成分分析中的常用算法。实际应用中,探地雷达接收的B-scan信号可以表示为矩阵WR∈RM×N,其中M为时间上的采样点数,N为某测线的测量点数目。对WR进行奇异值分解[1]:
| ${W_{\rm R}} = UD{V^T} = \sum\limits_{i = 1}^P {{u_i}{D_{i,i}}v_i^T}, P = min\{ M,N\} $ | (1) |
接收信号矩阵可以表示为${{\rm{W}}_{\rm{R}}}{\rm{ = }}{S_{\rm{R}}}{\rm{ + }}{D_{\rm{R}}}$,其中$S_{\rm R}$与$D_{\rm R}$分别为目标回波信号矩阵和杂波信号矩阵。由于在同一测线上的各个测量点的一些主要杂波,包括收发耦合波、地表直达波、地下媒质背景杂波等,往往变化不大,故可以认为这些杂波对应于强相关性的主成分;而接收信号中随机变化的噪声则对应弱相关的主成分。因此,去除能量较大和较小的分量,选取合适的主成分进行数据重构,不仅能够有效抑制杂波,而且可以抑制随机噪声。重构主成分的选取可按照方差贡献率得到[13]:
| $l = \sum\limits_{j = 1}^r {{D_{i,i}}} /\sum\limits_{i = 1}^P {{D_{i,i}}} $ | (2) |
经统计分析,一般情况下探地雷达B-scan图像经过主成分分析后,第1个主成分的贡献率往往在90%左右,而前10个主成分的贡献率可达到99.9%左右。因此,文中按照贡献率99.9%来选取合适的重构主成分。
传统的主成分分析方法对探地雷达A-scan数据时间窗具有整体性[8],即奇异值大小反映了A-scan数据道之间在整个时间轴上的相关性。若探测场地附近有大型施工或地质条件复杂时,会导致剖面部分区域探测结果道间强相关性[13]。若采用传统的主成分分析滤波算法,则有用回波信号就可能被滤除。
小波变换方法是在时频域内滤除随机噪声,小波通过尺度伸缩可改变时间和频率的分辨率,可以实现在不同尺度下的时频域处理。由于探地雷达回波信号是非平稳信号,故采用小波变换来处理探地雷达回波数据是比较合适的。2维小波变换是将原始图像分解为近似值、水平细节、垂直细节与对角细节部分,可对近似值多次分解,对图像剖分更细化。对2维小波变换得到的每个部分进行主成分分析,根据贡献率来选取主成分进行重构,对重构得到的各个部分信号进行2维小波反变换,即实现了2维小波域的主成分分析。
基于小波变换的主成分分析算法描述如下:
(1) 对原始探地雷达记录的回波数据进行2维小波变换,得到不同分解次数下近似值、水平细节、垂直细节与对角细节信号。小波变换分解次数决定于实际地质资料的复杂度,文中均采用一次小波分解。
(2) 对小波分解得到的不同信号进行主成分分析,取一定贡献率特征值进行重构。
(3) 对经主成分分析处理后的不同信号进行2维小波反变换。 3 自适应杂波抑制
自适应滤波可以随信号和杂波统计特性的变化而自动调整其参数,在提高杂波抑制效果的同时,能够较好地保证回波信号的保真度。为实现这一点需要找到一路与各测量点A-scan信号中杂波具有强相关性而与目标回波信号不相关或者弱相关的参考输入信号,通过自适应算法,动态调整数字滤波器的参数,使得参考信号经过滤波后能很好地抵消各测量点信号的直达波成分。因此,参考杂波信号,即期望信号的选取,是自适应滤波处理技术的一个核心。
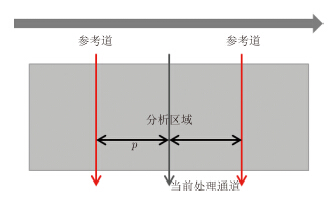
自适应滤波器的结构设计和自适应算法的选取则是另一核心[14]。为了增强滤波效果的鲁棒性,文中采用前后参考扫描的广义双边线性预测(TwoSidedLinearPrediction,TSLP)来实现滤波[15],其模型如图 1所示。其中自适应滤波器采用横向滤波器结构,自适应算法采用递推最小二乘准则。自适应滤波器参考输入信号选取提前、滞后的第$p$道($p$为参考步长)A-scan扫描来实现双边线性预测,即
|
图 1 双边线性预测方法示意图 Fig.1 Illustration of two-sided linear prediction approach |
| ${x_m} = \left[ {{x_{m - p}}{x_{m + p}}} \right]\left[ \matrix{ \theta \left( 0 \right) \hfill \cr \theta \left( 1 \right) \hfill \cr} \right] = {A_m}\hat \theta $ | (3) |
| $\hat \theta \left( n \right) = \hat \theta \left( {n - 1} \right) + K\left( n \right)\left( {{x_m}\left( n \right) - A_{_m}^{\rm T}\hat \theta \left( {n - 1} \right)} \right)$ | (4) |
| $K\left( n \right) = {{{\lambda ^{ - 1}}P\left( {n - 1} \right)A\left( n \right)} \over {1 + {\lambda ^{ - 1}}{A^{\rm T}}\left( n \right)P\left( {n - 1} \right)A\left( n \right)}}$ | (5) |
| $P\left( n \right) = {\lambda ^{ - 1}}P\left( {n - 1} \right) - {\lambda ^{ - 1}}K\left( n \right)A_{_m}^{\rm T}P\left( {n - 1} \right)$ | (6) |
主成分分析子空间投影法是基于探地雷达Bscan数据的2阶统计特性,寻求不相关的子空间投影,不同子空间的权重关系能够按照能量大小清晰地进行区分与筛选。基于小波变换的主成分分析法是按照一定的贡献率对小波分解得到的细节与近似部分进行主成分分析,有用目标信号则可能被去除或杂波信号没有完全被滤除。为解决这个问题,在基于小波变换的主成分分析法中,进一步结合自适应滤波技术。即将改进的主成分分析与上述的双边线性预测相结合。采用最小二乘自适应对改进的主成分分析子空间重构信号进行双边线性建模,能利用主成分分析对B-scan图像的全局性,具有更优的杂波抑制效果。这即是我们提出的基于小波变换的主成分分析自适应杂波抑制方法(Wavelet-PCATSLP)。
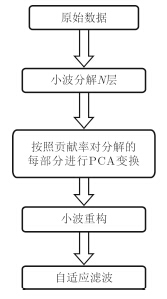
在Wavelet-PCA-TSLP算法中,首先对原始Bscan图像进行Wavelet-PCA分解,在分解结果中取适当子空间进行信号重构,再对所得PCA子空间重构信号进行2维小波反变换,即实现了Wavelet-PCA;对Wavelet-PCA得到的信号进行双边线性建模与最小二乘滤波,最终实现杂波去除。在小波分解之后的信号重构中,本文按照贡献率为99.9%来选取相应的主成分进行重构。双边距离$p$的选取应兼顾扫描道之间的相似性与差异性;若$p$过小,则会由于参考范围过窄而失去了“预测”的意义;若$p$过大,则会因参考扫描道的性质差异过大而失准,$p$一般可取几道至几十道[16]。本文双边距离$p$取8。Wavelet-PCA-TSLP方法流程图如图 2所示。
|
图 2 Wavelet-PCA-TSLP流程图 Fig.2 Flow of Wavelet-PCA-TSLP algorithm |
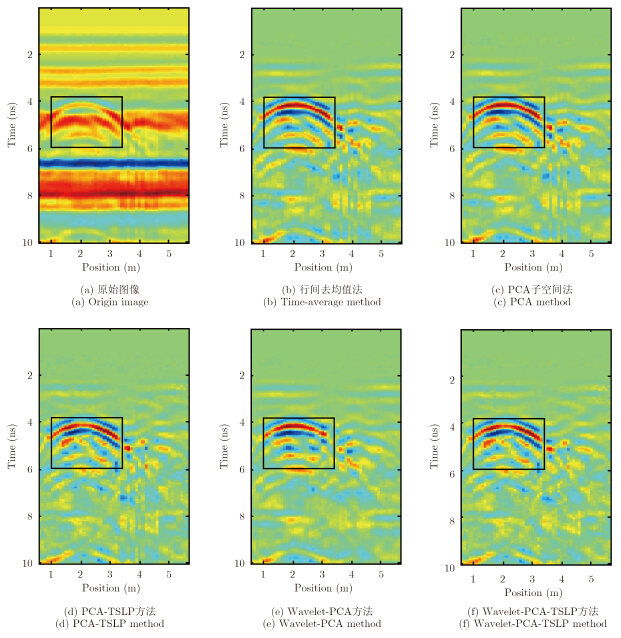
实验选用了两组不同GPR系统的实测数据。其中实测数据1来自国防科技大学电子科学与工程学院遥感信息处理实验室的RadarEye高分辨率GPR系统,该系统使用分布式电阻加载超宽带喇叭天线;实验中将一个反步兵塑料雷埋于沙箱中,沙箱尺寸为4m×3m×1m(长×宽×高);反步兵塑料雷直径为11.2cm,厚度为5.55cm,中心埋深为17cm;沙子的相对介电常数为2.15;天线高度为38.6cm;天线发射信号为高斯微分脉冲,中心频率为1GHz,时间窗为10ns,采样点数设置为512[17]。图 3的6幅图从上到下从左到右所用的算法依次是:原始图像、B-scan图像行间去均值法、PCA子空间法、PCA-TSLP方法、本文的Wavelet-PCA方法及Wavelet-PCA-TSLP方法。
|
图 3 第1组数据的实验结果 Fig.3 Results of first B-scan targets after clutter reduction |
本文采用信杂比与目标图像熵来比较杂波抑制效果。将B-scan图像表示为$W[M×N]$,目标区域的子图像表示为$T[I×J]$。显然,杂波抑制效果越好,目标信号及伪目标信号与背景信号的对比越明显,目标信号能量越高且信号特征越清晰。利用平均功率法计算信杂比[16]:
| $\rm {SCR} = {{\sum\limits_{i = 1}^I {\sum\limits_{i = 1}^J {{T^2}\left( {i,j} \right)/\left( {IJ} \right)} } } \over {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{W^2}\left( {m,n} \right)/\left( {MN} \right)} } }}$ | (7) |
目标图像熵的计算公式[18]为:
| $Q = {{{{\left( {\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {{T^2}\left( {i,j} \right)} } } \right)}^2}} \over {\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {{T^4}\left( {i,j} \right)} } }}$ | (8) |
图像熵表示的是整个目标图像的信息量。熵越大,图像越混乱。反之,熵越小,图像越清晰。本文中算法运行计算机处理器为主频3.10GHz的AMDAthlon(tm)IIX2CPU,内存2.00GB。各种方法的杂波抑制性能对比如表 1所示。
| 表 1 不同方法对实验数据1的运行时间、信杂比与目标图像熵对比结果 Tab. 1 Comparison between results of first B-scan on time cost, SCR and entropy using different approaches |
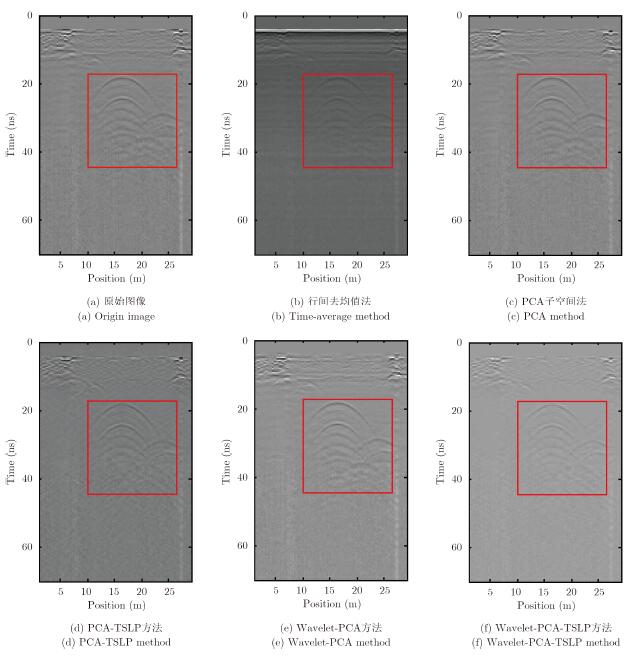
实测数据2来自于意大利IDS公司的RIS-K2探地雷达对某公路目标的探测结果。探测中采用中心频率为900MHz的屏蔽天线,天线为单发单收天线,距离地面高度为20mm,探测接收时间窗大小设置为70ns,采样点数设置为512。实测数据2实验结果如图 4所示,各种方法的杂波抑制性能对比如表 2所示。
|
图 4 第2组数据的实验结果 Fig.4 Results of second B-scan targets after clutter reduction |
| 表 2 不同方法对实验数据2的运行时间、信杂比与目标图像熵对比结果 Tab. 2 Comparison between results of second B-scan on time cost,SCR and entropy using different approaches |
实验中目标子图像区域分别如图 3中黑色矩形与图 4中红色矩形所示。不同方法对两组数据的实验结果表明:(1)Wavelet-PCA方法与PCA方法相比,能在较小降低信杂比的条件下增加目标清晰度,或者在降低目标清晰度的条件下增加整个信杂比;Wavelet-PCA方法是对小波变换后的细节与近似部分进行主成分分析,故可能导致在增加信杂比时降低了目标图像熵或者降低目标图像熵时降低了信杂比。(2)自适应滤波增加了目标图像的清晰度;PCA-TSLP方法与PCA方法相比,能在降低信杂比的同时增加目标图像清晰度;Wavelet-PCA-TSLP方法与Wavelet-PCA方法相比,能增加目标清晰度;(3)当处理数据较小时,Wavelet-PCA方法运行时间较PCA方法短,如第1组数据处理结果所示;处理数据较大时,Wavelet-PCA方法运行时间较长,如第2组数据处理结果所示;Wavelet-PCA方法运行时间直接影响了Wavelet-PCA-TSLP运行时间。总之,Wavelet-PCA-TSLP方法在图像信杂比与目标图像清晰度综合方面具有良好的效果。 5 结论
主成分分析子空间投影法在探地雷达杂波抑制应用中表现出了其有效性,尤其在直达波抑制中,但是存在缺乏细节分析及横向分辨率不高的问题,为此提出了基于2维小波变换的改进主成分分析子空间投影法。为了进一步提高杂波抑制效果,充分利用基于线性预测模型的自适应横向滤波方法具有良好的目标回波信号保真度与学习适应能力,在杂波抑制处理中引入自适应横向滤波,形成了Wavelet-PCA-TSLP方法。这种方法将主成分分析对B-scan数据的全局性分析能力、小波变换分时分频的细节分析能力、以及自适应滤波的良好统计特性参数调节能力结合在一起,使得杂波抑制性能得到综合提高。实验结果表明,所提方法在信杂比与目标图像熵方面具有更好的性能,杂波抑制效果优于其它方法。
| [1] | 粟毅, 黄春琳, 雷文太. 探地雷达理论与应用[M]. 北京: 科学出版社, 2006: 120–122. Su Yi, Huang Chun-lin, and Lei Wen-tai. Theory and Application of Ground Penetrating Radar[M]. Beijing: Science Press, 2006: 120–122.( 2) 2) |
| [2] | 吴仁彪, 刘家学, 张蓓. 探地雷达地杂波抑制方法研究进展[J]. 信号处理, 2005, 21(4A): 510–513. Wu Ren-biao, Liu Jia-xue, and Zhang Bei. Survey on GPR ground bounce removal[J]. Signal Processing, 2005, 21(4A): 510–513.(  1) 1) |
| [3] | Van der Merwe A and Gupta I J. A novel signal processing technique for clutter reduction in GPR measurements of small, shallow land mines[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(6): 2627–2637.( 1) 1) |
| [4] | Brunzell H. Detection of shallowly buried objects using impulse radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(2): 875–886.( 1) 1) |
| [5] | 高守传, 粟毅, 黄春琳, 等. 用平均法实现瞬态信号接收中的直达波抑制[J]. 系统工程与电子技术, 2004, 26(1): 21–25. Gao Shou-chuan, Su Yi, Huang Chun-lin, et al.. Using of mean-subtraction method to suppress the direct wave in instantaneous signal receiving[J]. Systems Engineering and Electronics, 2004, 26(1): 21–25.(  1) 1) |
| [6] | 高倩, 吴仁彪, 米琦. 基于核ICA的探地雷达地杂波抑制[J]. 现代雷达, 2007, 29(3): 23–27. Gao Qian, Wu Ren-biao, and Mi Qi. Kernel ICA for ground bounce removal with GPR[J]. Modern Radar, 2007, 29(3): 23–27.(  1) 1) |
| [7] | 王萧. 基于KPCA的探地雷达自适应杂波抑制算法研究[J]. 现代电子技术, 2014, 37(11): 31–33. Wang Xiao. Research on KPCA-based adaptive clutter rejection algorithm for GPR[J]. Modern Electronics Technique, 2014, 37(11): 31–33.(  1) 1) |
| [8] | 申家全, 闫怀志, 胡昌振[8] . 基于主成分自动选择准则的探地雷达杂波抑制[J]. 电波科学学报, 2010, 25(1): 83–87. Shen Jia-quan, Yan Huai-zhi, and Hu Chang-zhen. Autoselected rule on principal component analysis in ground penetrating radar signal denoising[J]. Chinese Journal of Radio Science, 2010, 25(1): 83–87. (  2) 2) |
| [9] | 张蓓, 刘家学, 吴仁彪. 探地雷达子空间地杂波抑制方法研究[J]. 信号处理, 2005, 21(4A): 514–517. Zhang Bei, Liu Jia-xue, and Wu Ren-biao. Research on subspace-based GPR ground bounce removel method[J]. Signal Processing, 2005, 21(4A): 514–517.(  1) 1) |
| [10] | 杨凤娟, 范运岭. 一种改进的滤除探地雷达直耦波的算法[J]. 地球物理学进展, 2013, 28(3): 1617–1625. Yang Feng-juan and Fan Yun-ling. An improved filter algorithm of direct arrive wave for GPR[J]. Progress in Geophysics, 2013, 28(3): 1617–1625.(  1) 1) |
| [11] | 陈文超, 师振盛, 汪文秉, 等. 小波变换在去除探地雷达信号直达波的应用[J]. 电波科学学报, 2000, 15(3): 352–357. Chen Wen-chao, Shi Zhen-sheng, Wang Wen-bing, et al.. Suppressing the direct wave noise in GPR data using the 2- D continue directional wavelets[J].Chinese Journal of Radio Science, 2000, 15(3): 352–357.(  1) 1) |
| [12] | 包乾宗, 陈文超, 高静怀, 等. 探地雷达直达波衰减的Curvelet变换方法[J]. 电波科学学报, 2008, 23(3): 449–454. Bao Qian-zong, Chen Wen-chao, Gao Jing-huai, et al.. Direct wave attenuation technique of GPR by curvelet transform[J]. Chinese Journal of Radio Science, 2008, 23(3): 449–454.(  1) 1) |
| [13] | 李才明, 王良书, 徐鸣洁, 等. 基于小波能谱分析的岩溶区探地雷达目标识别[J]. 地球物理学报, 2006, 49(5): 1499–1504. Li Cai-ming, Wang Liang-shu, Xu Ming-jie, et al.. Objects recognition of ground penetrating radar in karst regions using wavelet energy spectrum analysis[J].Chinese Journal of Geophysics, 2006, 49(5): 1499–1504.(  2) 2) |
| [14] | 高守传, 黄春琳, 粟毅. 基于RLS横向滤波自适应抵消法的直达波抑制[J]. 信号处理, 2004, 20(6): 566–571. Gao Shou-chuan, Huang Chun-lin, and Su Yi. Direct wave suppression based on adaptive interference canceling method[J]. Signal Processing, 2004, 20(6): 566–571.(  1) 1) |
| [15] | Chan Thomas T C, So H C, and Ho K C. Generalized twosided linear prediction approach for land mine detection[J]. Signal Processing, 2008, 88(4): 1053–1060.( 1) 1) |
| [16] | 高翔, 姬光荣, 王群, 等. 主元子空间自适应双边预测探地雷达杂波抑制[J]. 电波科学学报, 2010, 25(2): 253–258. Gao Xiang, Ji Guang-rong, Wang Qun, et al.. Clutter reduction for landmine detection using adaptive two-sided linear prediction in PCA subspace[J]. Chinese Journal of Radio Science, 2010, 25(2): 253–258.(  2) 2) |
| [17] | 周琳. 探地雷达成像技术研究[D]. [博士论文], 国防科学技术大学, 2012: 44–45. Zhou Lin. Research on ground penetrating imaging techniques[D]. [Ph.D. dissertation], National University of Defense Technology, 2012: 44–45.(  1) 1) |
| [18] | 申家全, 闫怀志, 胡昌振. 基于图像熵的探地雷达杂波抑制效果评价[J]. 电波科学学报, 2011, 26(2): 267–271. Shen Jia-quan, Yan Huai-zhi, and Hu Chang-zhen. Evaluation method based on image entropy for clutter suppression effect of ground-penetrating radar[J]. Chinese Journal of Radio Science, 2011, 26(2): 267–271.(  1) 1) |
 2015, Vol. 4 Issue (4): 445–451
2015, Vol. 4 Issue (4): 445–451
