1 引言
在雷达目标的相干检测领域,杂波和目标模型的建立以及检测器设计是两大类基本问题[1]。在高斯杂波中,如果检测单元的杂波协方差矩阵已知,则最优检测器由白化滤波器与匹配滤波器级联组成。然而,杂波协方差矩阵通常是未知的,需要利用与检测单元邻近的参考单元数据进行估计,形成自适应检测器[2]。检测单元的杂波协方差矩阵可以与参考单元完全相同,也可以相差一个功率失配因子,这两种情况分别称为均匀杂波和部分均匀杂波。自Kelly的广义似然比(Generalized Likelihood Ratio Test,GLRT)检测器被提出以来[2],已有大量文献围绕均匀和部分均匀杂波中的自适应检测问题展开研究,并设计了一系列检测器。比如,Robey等人的自适应匹配滤波(Adaptive Matched Filter,AMF)检测器[3]、自适应子空间检测器(Adaptive Subspace Detectors,ASD)[4]、恒虚警(Constant False Alarm Rate,CFAR)自适应子空间检测器(CFAR ASD)[4]等。CFAR ASD又称为自适应相干估计器(Adaptive Coherence Estimator,ACE),在部分均匀杂波中,ACE是尺度不变的GLRT[5],同时也是极大不变(maximal Invariant)检测量和一致最优不变(Uniformly Most Powerful Invariant,UMPI)检测量[6]。在复合高斯杂波中,ACE还与自适应归一化匹配滤波(Adaptive Normalized Matched Filter,ANMF)检测器等价[7, 8, 9]。
Reed,Mallett和Brennan(RMB)的研究成果表明,如果雷达的相干脉冲数为 ${N_{\rm{p}}}$ ,为使自适应检测器得到满意的检测性能,在估计协方差矩阵时要求参考单元数 $K > 2{N_{\rm{p}}}$ (又称RMB准则[10])。然而,实际应用中受杂波尖峰、阵列配置、异常数据等因素的影响[11],与检测单元协方差矩阵相一致的参考单元数往往有限,在RMB准则约束下所选择的参考单元中难免会出现非均匀样本。在这种非均匀背景下,自适应检测器将出现检测性能损失,且无法保持CFAR特性[12, 13]。
为有效减小参考单元非均匀性对检测性能的影响,公开文献开展了大量研究,其中基于知识(Knowledge-Based,KB)的处理方法得到普遍认可,根据先验知识利用阶段的不同,可以将解决途径归结为间接法和直接法两类[14, 15, 16]。间接法的核心是参考单元数据选择技术[11, 17],该方法在保持检测器结构不变的前提下,依据一定的准则选择出与检测单元相一致的参考单元来估计杂波协方差矩阵,从而实现检测性能的改善,文献[11]中基于知识的数据选择准则以及文献[17]中基于功率的数据选择准则都属于该类方法。间接法的不足在于所需求的初始参考单元数较多[16],而直接法可以有效克服这种不足。直接法的核心思想是:在检测器设计阶段,充分考虑并利用杂波协方差矩阵在结构(比如斜对称结构、Toeplitz结构、圆结构等[18, 19])、先验分布(比如Wishart分布、逆Wishart分布等[15, 16])以及参数模型(比如1~4阶的AR模型[20, 21, 22])等方面的先验信息,以弱化RMB准则的约束,即减小协方差矩阵估计对参考单元数的需求,并以此来应对均匀参考单元数不足的问题,最终实现检测性能的提升。
本文重点关注直接法中利用杂波协方差矩阵结构信息的自适应检测问题。事实上,在阵列雷达中,如果天线为均匀线阵(Uniform LinearArray,ULA),即各阵元关于其相位中心具有对称间隔,或者相干脉冲串具有对称间隔,那么杂波协方差矩阵具有双重对称结构,即关于主对角线的Hermitian结构以及关于次对角线的斜对称结构[18]。在高斯背景下,文献[18]推导了斜对称协方差矩阵的最大似然估计,奠定了斜对称自适应检测方法的基础。文献[23]研究了均匀杂波中基于斜对称GLRT(Persymmetric GLRT,P-GLRT)的多波段目标自适应检测问题,并推导了检测概率和虚警概率的封闭表达式。文献[24]将文献[23]中的均匀杂波背景扩展到部分均匀杂波背景,建立了秩1目标的P-GLRT自适应检测器。文献[25]在文献[24]的基础上对检测准则进行了扩展,设计了部分均匀杂波中基于Rao检验和Wald检验的自适应检测器。文献[26]利用一个酉矩阵将斜对称导向矢量和斜对称协方差矩阵分别变换为实矢量和实对称矩阵,并建立了均匀高斯杂波中的斜对称AMF检测器和球不变随机矢量(Spherically Invariant Random Vectors,SIRV)杂波中的斜对称ANMF检测器,证明了其CFAR特性,同时在检测统计量等价统计分解的基础上推导了虚警概率的封闭表达式,最后又采用仿真数据、地杂波和海杂波数据进行了检测性能分析。文献[27]对SIRV杂波中的斜对称检测器进行了扩展,研究了纹理分量建模为Gamma分布和逆Gamma分布情况下的自适应检测问题。文献[28]在文献[24]和文献[26]的基础上,一方面采用两步GLRT建立了部分均匀杂波中的斜对称ACE检测器,并推导了虚警概率和检测概率的表达式,另一方面补充推导了文献[26]中斜对称AMF检测器的检测概率表达式。此外,文献[29]和文献[30]分别研究了具有干扰目标抑制能力的斜对称检测问题和分布式目标的斜对称检测问题。如果杂波建模为多通道AR模型,则相应的斜对称检测器已在文献[31]中给出。上述检测器对协方差矩阵斜对称结构的利用均体现在检测器设计阶段,如果仅在协方差矩阵估计阶段考虑其斜对称结构,那么相应的检测器已在文献[32]和文献[33]中给出,并在文献[34]和文献[35]中利用实测数据对检测性能进行了分析。
从研究现状来看,在斜对称检测器设计时对杂波模型的考虑较为全面,从均匀杂波到部分均匀杂波,再到SIRV杂波,均有所研究。然而,在目标模型方面的考虑较为单一,已有斜对称检测器中采用的秩1目标模型仅包含一个自由度,相比之下,多维子空间目标模型更加符合实际情况[1, 4, 36]。许多情况都会引起目标信号多维,例如,当目标相对于雷达视角除平动之外,还存在相对于雷达视角的转动时,目标信号将出现多个彼此不同的特征多普勒频率,此时就需要将目标信号建模为多维子空间模型。
本文主要研究均匀和部分均匀杂波中,多维子空间目标的斜对称自适应检测问题。首先,在保持目标特征参数不变的前提下,对目标模型做等价变换使其具有斜对称结构。然后,分别采用一步GLRT和两步GLRT推导斜对称自适应检测器。最后,通过Monte Carlo仿真,分析比较斜对称自适应检测器与已有检测器的性能差异,并从协方差矩阵估计方法的影响等方面对检测性能进行综合分析。
2 问题描述和检测模型
假设ULA的阵元数为 ${N_{\rm{a}}}$ ,在相干处理间隔(Coherent Processing Interval,CPI)内发射 ${N_{\rm{p}}}$ 个相干脉冲,接收机对回波信号进行了解调、匹配滤波和采样,那么单个距离单元上的采样数据按列堆排列后形成一个 $N \times 1(N = {N_{\rm{a}}}{N_{\rm{p}}})$ 维复矢量。可能包含目标信号的距离单元称为检测单元,与之邻近且仅包含杂波的距离单元称为参考单元。所要解决的目标检测问题可以描述为如下的二元假设检验[24]:
|
$\left\{ \matrix{
{{\rm{H}}_0}:{\rm{ }}{\bf{z}} = {\bf{c}},{\rm{ }}{{\bf{z}}_k} = {{\bf{c}}_k},{\rm{ }}k = 1, \cdots ,K \hfill \cr
{{\rm{H}}_1}:{\rm{ }}{\bf{z}} = {\bf{s}} + {\bf{c}},{\rm{ }}{{\bf{z}}_k} = {{\bf{c}}_k},{\rm{ }}k = 1, \cdots ,K \hfill \cr} \right.$
|
(1)
|
其中, $z$ 和 ${z}_k$ 分别表示检测单元和参考单元的观测数据, $s$ 表示目标信号, $c$ 和 ${c}_k$ 分别表示检测单元和参考单元的杂波。以上数据均为 $N \times 1$ 维复矢量,本文仅考虑一个阵元的情况,此时 $N$ 即为相干脉冲数。
假定杂波建模为统计独立的零均值复高斯随机矢量,在部分均匀杂波中,杂波协方差矩阵为[24]:
|
$\left\{ \matrix{
E({\bf{c}}{{\bf{c}}^{\rm{H}}}) = {\bf{M}} \hfill \cr
E({{\bf{c}}_k}{\bf{c}}_k^{\rm{H}}) = \gamma {\bf{M}},{\rm{ }}k = 1, \cdots ,K \hfill \cr} \right.$
|
(2)
|
其中, $( \cdot )$
H表示共轭转置, $\rm{E}(\cdot )$ 表示期望,参数 $\gamma (\gamma > 0)$ 表示检测单元和参考单元杂波的功率失配因子,当 $\gamma = 1$ 时,背景将简化为均匀杂波。
目标信号 $s$ 建模为多维子空间模型,即假定目标信号处在观测空间的有限维线性子空间上[1],采用高斯线性模型[1, 4]建模子空间目标,即
|
${\bf{s}} = {{\bf{U}}_{\rm{S}}}{\bf{b}}$
|
(3)
|
其中, ${U}_S$ 是维数为 $N \times r$ 的模式矩阵, ${U}_S$ 的秩满足 ${\rm{rank(}}{{U}_{\rm{S}}}) = r \lt N$ , $b$ 是 $r \times 1$ 维的位置矢量,表示目标子空间的坐标。对于该模型,目标信号处在由 ${U}_S$ 的列矢量张成的线性子空间 $\langle {{\bf{U}}_{\rm{S}}}\rangle $ 上, ${U}_S$ 的秩反映了目标的不确定度。在检测器设计时通常假定 ${U}_S$ 已知,而 $b$ 未知,它可以建模为确定性未知矢量或复高斯随机矢量
[1, 36]。在实际应用中, ${U}_S$ 的秩可以从实测数据中估计得到,而目标子空间可以用超分辨谱估计算法得到
[36]。当 $r = 1$ ,即目标子空间的维数为1时,子空间目标退化为秩1目标,目标模型简化为 $s = \alpha {p}$ ,其中, $p$ 表示导向矢量, $\alpha $ 表示未知的目标复幅度,它与目标的雷达截面积(Radar Cross Section,RCS)和传播通道的性质有关。
对于上述检测问题,在H0条件下,检测单元和参考单元观测数据的联合概率密度函数(Probability Density Function,PDF)为[24]:
|
$\begin{aligned}
\mathit{f}_{\rm{0}} & = f({z},{{z}_1},\cdots ,{{z}_K}|{M},\gamma ,{{\rm{H}}_0})\\
& = \frac{1}{{{\gamma ^{NK}}{{\left[{{{π} ^N}\det ({M})} \right]}^{K + 1}}}}{\rm{etr(}} - {{M}^{ - 1}}{{T}_0})
\end{aligned}$
|
(4)
|
在H
1条件下,联合PDF为:
|
$\eqalign{
& {f_1} = f({\bf{z}},{{\bf{z}}_1}, \cdots ,{{\bf{z}}_K}|{\bf{M}},{\bf{b}},\gamma ,{{\rm{H}}_1}) \cr
& \quad {\rm{ }} = {1 \over {{\gamma ^{NK}}{{\left[ {{\pi ^N}\det ({\bf{M}})} \right]}^{K + 1}}}}{\rm{etr(}} - {{\bf{M}}^{ - 1}}{{\bf{T}}_1}{\rm{)}} \cr} $
|
(5)
|
其中,det $( \cdot )$ 表示矩阵的行列式,etr $( \cdot )$ 表示矩阵迹的指数函数,其余参数的表达式如下:
|
${{T}_0} = {z}{{z}^{\rm{H}}} + \frac{1}{\gamma }{S} \quad \quad \quad \quad \quad \quad\quad \quad $
|
(6)
|
|
${{T}_1} = ({z} - {{U}_{\rm{S}}}{b}){({z} - {{U}_{\rm{S}}}{b})^{\rm{H}}} + \frac{1}{\gamma }{S}$
|
(7)
|
|
${S} = \sum\limits_{k = 1}^K {{{z}_k}{z}_k^{\rm{H}}} \quad \quad \quad \quad \quad \quad \quad\quad \quad \ $
|
(8)
|
根据Neyman-Pearson(NP)准则,该检测问题可以用GLRT解决,其中未知参数集合为:
|
${Ω}: \{{M,b},\gamma \} $
|
(9)
|
基于GLRT的检测器可表示为式(10)形式:
|
$\frac{{\begin{array}{*{20}{c}}
{\max } \\
M
\end{array}\begin{array}{*{20}{c}}
{\max } \\
b
\end{array}\begin{array}{*{20}{c}}
{\max } \\
\gamma
\end{array}\begin{array}{*{20}{c}}
{{f_1}} \\
{}
\end{array}}}{{\begin{array}{*{20}{c}}
{\max } \\
M
\end{array}\begin{array}{*{20}{c}}
{\max } \\
\gamma
\end{array}\begin{array}{*{20}{c}}
{{f_0}} \\
{}
\end{array}}}\mathop {\mathop > \limits_ < }\limits_{{{\text{H}}_0}}^{{{\text{H}}_{\text{1}}}} G$
|
(10)
|
3 斜对称GLRT检测器设计
3.1 杂波和目标模型的斜称性结构
假定杂波协方差矩阵 ${M}$ 同时具有Hermitian结构和斜对称结构,即 ${M}$属于一类具有双重对称结构的矩阵集合 ${{M}_{\rm{p}}}$ ,满足[23, 32]:
|
${\bf{M}} \in {{\bf{M}}_{\rm{p}}} = \{ {{\bf{M}}_{\rm{p}}}|{{\bf{M}}_{\rm{p}}} = {\bf{M}}_{\rm{p}}^{\rm{H}}{\rm{, and }}{{\bf{M}}_{\rm{p}}} = {\bf{JM}}_{\rm{p}}^ * {\bf{J}}\} $
|
(11)
|
其中, $( \cdot )$ 表示共轭, ${\bf{J}}$ 表示置换矩阵,即
|
${J} = \left[{\begin{array}{l}
\hspace{5pt}0 \hspace{15pt} 0 \hspace{15pt} \cdots \hspace{15pt} 0 \hspace{15pt} 1 \hspace{5pt}\\
\hspace{5pt}0 \hspace{15pt} 0 \hspace{15pt} \cdots \hspace{15pt} 1 \hspace{15pt} 0 \hspace{5pt}\\
\hspace{5pt}\vdots \hspace{17pt} \vdots \hspace{17pt} \ddots \hspace{15pt} \vdots \hspace{18pt} \vdots \hspace{5pt}\\
\hspace{5pt}1 \hspace{15pt} 0 \hspace{15pt} \cdots \hspace{15pt} 0 \hspace{15pt} 0 \hspace{5pt}
\end{array}} \right] $
|
(12)
|
在检测器设计阶段,对协方差矩阵Hermitian结构的利用较为充分,若在此基础上进一步考虑其斜对称结构,将有效减小协方差矩阵估计对参考单元数的需求
[23]。
对于目标而言,在秩1假设下,保持目标特征参数(比如多普勒频率)不变,通过导向矢量数学表示形式的等价变换可以使目标模型具有斜对称结构,即满足 ${\bf{p}} = {\bf{J}}{{\bf{p}}^ * }$ [23, 24]。而对于多维子空间目标,首先要按照同样的思路进行等价变换,使其具有斜对称结构。采用与高斯线性模型等价的模型描述子空间目标,即[36]
其中,
E表示导向矩阵, ${a}$ 表示目标主散射体的幅度矢量。将
E进行奇异值分解,即,${\bf{E}} = {{\bf{U}}_{\rm{S}}}{\Lambda }{\bf{V}}_{\rm{S}}^{\rm{H}}$,则 ${{\bf{U}}_{\rm{S}}}$ 即为高斯线性模型中的模式矩阵,它是一个酉矩阵。 ${a}$可以建模为确定性未知矢量或者复高斯随机矢量,它与位置矢量 ${b}$ 的对应关系为 ${\bf{b}} = {\Lambda }{\bf{V}}_{\rm{S}}^{\rm{H}}{\bf{a}}$
[1]。本文仅考虑 ${b}$ 建模为确定性未知矢量的情况,对应的目标模型又称为1阶高斯(First-Order Gaussian,FOG)模型
[37]。对于秩 $r$ 子空间目标, ${E}$ 可以表示为:
|
${E} = {\left( {\begin{array}{l}
\hspace{14pt} 1 \hspace{43pt} 1 \hspace{22pt} \cdots \hspace{23pt} 1\\
{{\rm{e}^{\rm{j}{\varphi _1}(1)}}} \hspace{25pt} {{\rm{e}^{\rm{j}{\varphi _2}(1)}}} \hspace{16pt} \cdots \hspace{13pt} {{\rm{e}^{\rm{j}\mathit{\varphi _r}(1)}}}\\
\hspace{15pt} \vdots \hspace{45pt} \vdots \hspace{22pt} \ddots \hspace{22pt} \vdots \\
{{\rm{e}^{\rm{j}{\varphi _1}({N} - 1)}}} \hspace{13pt} {{\rm{e}^{\rm{j}{\varphi _2}({N} - 1)}}} \hspace{7pt} \cdots \hspace{11pt} {{\rm{e}^{\rm{j}\mathit{\varphi _r}({N} - 1)}}}
\end{array}} \right)_{{N} \times r}}$
|
(14)
|
其中, ${E}$ 的秩满足 ${\rm{rank(}}{E}{\rm{)}} = r \lt N$ ,假定观测时间内目标运动速度较慢,则相位 ${\varphi_r}(n)$ 线性变化,即
|
$ {\mathit{\varphi}_r}(n) = 2π {\mathit{f}_r}n,\ n = 0,1,\cdots ,N - 1$
|
(15)
|
为使子空间目标模型具有斜对称结构,在保持目标特征参数(即相位)不变的前提下,对E的所有列向量都进行等价变换,其中,当 $N$ 为偶数时, ${E}$ 变换为:
|
${E} = {\left({\begin{array}{l}
{{\rm{e}^{ - \rm{j}{\varphi _1}\left( \large{ \frac{{{N} - 1}}{2}} \right)}}} \hspace{5pt} {{\rm{e}^{ - \rm{j}{\varphi _2}\left( \large{\frac{{{N} - 1}}{2}} \right)}}} \hspace{5pt} \cdots \hspace{5pt} {{\rm{e}^{ - \rm{j}{\varphi _r}\left( \large{\frac{{{N} - 1}}{2}} \right)}}}\\
\hspace{15pt} \vdots \hspace{45pt} \vdots \hspace{21pt} \quad \ddots \hspace{22pt} \vdots \\
{{\rm{e}^{ - \rm{j}{\varphi _1}/2}}} \hspace{25pt} {{\rm{e}^{ - \rm{j}{\varphi _2}/2}}} \hspace{8pt} \quad \cdots \hspace{7pt} {{\rm{e}^{ - \rm{j}{\varphi _r}/2}}}\\
{{\rm{e}^{\rm{j}{\varphi _1}/2}}} \hspace{30pt} {{\rm{e}^{\rm{j}{\varphi _2}/2}}} \hspace{14pt} \quad \cdots \hspace{7pt} {{\rm{e}^{\rm{j}{\varphi _r}/2}}}\\
\hspace{15pt} \vdots \hspace{45pt} \vdots \hspace{21pt} \quad \ddots \hspace{22pt} \vdots \\
{{\rm{e}^{\rm{j}{\varphi _1}\left( \large{\frac{{{N} - 1}}{2}} \right)}}} \hspace{20pt} {{\rm{e}^{\rm{j}{\varphi _2}\left( \large{\frac{{{N} - 1}}{2}} \right)}}} \hspace{1pt} \cdots \hspace{7pt} {{\rm{e}^{\rm{j}{\varphi _r}\left( \large{\frac{{{N} - 1}}{2}} \right)}}}
\end{array}} \right)_{N \times r}}$
|
(16)
|
当 $N$ 为奇数时, ${E}$ 变换为:
|
${E} = {\left( {\begin{array}{l}
{{\rm{e}^{ - \rm{j}{\varphi _1}\left( \large{\frac{{{N} - 1}}{2}} \right)}}} \hspace{5pt} {{\rm{e}^{ - \rm{j}{\varphi _2}\left( \large{\frac{{{N} - 1}}{2}} \right)}}} \hspace{5pt} \cdots \hspace{5pt} {{\rm{e}^{ - \rm{j}\mathit{\varphi _r}\left( \large{\frac{{{N} - 1}}{2}} \right)}}}\\
\hspace{15pt} \vdots \hspace{45pt} \vdots \hspace{21pt} \quad \ddots \hspace{25pt} \vdots \\
\hspace{14pt} 1 \hspace{43pt} 1 \hspace{21pt} \quad \cdots \hspace{23pt} 1\\
\hspace{15pt} \vdots \hspace{45pt} \vdots \hspace{22pt} \quad \ddots \hspace{25pt} \vdots \\
\hspace{5pt} {{\rm{e}^{j{\varphi _1}\left( \large{\frac{{{N} - 1}}{2}} \right)}}} \hspace{10pt} {{\rm{e}^{\rm{j}{\varphi _2}\left( \large{\frac{{{N} - 1}}{2}} \right)}}} \hspace{6pt} \cdots \hspace{9pt} {{\rm{e}^{\rm{j}\mathit{\varphi _r}\left( \large{\frac{{{N} - 1}}{2}} \right)}}}
\end{array}} \right)_{N \times r}}$
|
(17)
|
从本质上讲,该变换是将目标信号的观测描述为以相干脉冲串的中心为起始时刻的形式,变换前后导向矩阵所携带的目标特征信息完全相同,因此它们是一一对应的关系。显然,变换后${E}$ 具有斜对称结构,即满足 ${E} = {J}{E}^ * $ 。下面将证明,如果 ${E}$ 是斜对称的,那么高斯线性模型中的模式矩阵 ${U}_{\rm{S}}$ 也具有斜对称结构,即如下的性质,这是下一步斜对称GLRT检测器设计的基础。
性质1 对于维数为 $N \times r(r \lt N)$ ,秩为 $r$ 的矩阵 ${E}$ ,其奇异值分解为 ${E} = {U}_{\rm{S}}{Λ}\! \! {V}_{\rm{S}}^{\rm{H}}$ ,如果 ${E}$ 满足 ${E} = {J}{E}^ * $ ,则 ${U}_{\rm{S}}$ 满足 ${U}_{\rm{S}} = {JU}_{\rm{S}}^ * $ 。
证明由于 ${\rm{rank(}}{E}{\rm{)}} = r \lt N$ ,奇异值分解后,令 ${\sigma _{\rm{1}}} \ge {\sigma _{\rm{2}}} \ge \cdots \ge {\sigma _r} \gt 0$ 为 ${E}$ 的 $r$ 个非零奇异值,则 ${Λ} = {\rm{diag(}}{\sigma _{\rm{1}}},{\sigma _{\rm{2}}},\,\cdots \,,{\sigma _r}{\rm{)}}$ 。
令
|
${U}_{\rm{S}} = [{{u}_1} \ {{u}_2}{\rm{ }} \,\cdots \,{\rm{ }}{{u}_r}]$ , ${{\bf{V}}_{\rm{S}}} = [{{\bf{v}}_1}{\rm{ }}{{\bf{v}}_2}{\rm{ }} \cdots {\rm{ }}{{\bf{v}}_r}]$
|
那么奇异值分解可重新表示为:
|
${E} = {{U}_{\rm{S}}}{Λ} \! \! {V}_{\rm{S}}^{\rm{H}} = \sum\limits_{i = 1}^r {{\sigma _i}{{{u}}_i}{{v}}_i^{\rm{H}}} $
|
(18)
|
等式两端分别取共轭,得
|
${E}^ * = \sum\limits_{i = 1}^r {{\sigma _i}{{u}}_i^ * {{({{v}}_i^{\rm{H}})}^ * }} = \sum\limits_{i = 1}^r {{\sigma _i}{{u}}_i^ * {{v}}_i^{\rm{T}}} $
|
(19)
|
其中, $( \cdot )$
T表示转置。将 $N \times N$ 维的置换矩阵
J分别左乘式(19)两端,得
|
${J}{{{E}}^ * } = {{J}}\sum\limits_{i = 1}^r {{\sigma _i}{{u}}_i^ * {{v}}_i^{\rm{T}}} = \sum\limits_{i = 1}^r {{\sigma _i}({{Ju}}_i^ * ){{v}}_i^{\rm{T}}} $
|
(20)
|
由于 ${E}$ 满足 ${{E}} = {{J}}{{{E}}^ * }$ ,因此
|
${{E}} = \sum\limits_{i = 1}^r {{\sigma _i}{{{u}}_i}{{v}}_i^{\rm{H}}} = \sum\limits_{i = 1}^r {{\sigma _i}({{Ju}}_i^ * ){{v}}_i^{\rm{T}}} $
|
(21)
|
即
|
$\sum\limits_{i = 1}^r {{\sigma _i}\left[{{{{u}}_i}{{v}}_i^{\rm{H}} - ({\ {Ju}}_i^ * ){{v}}_i^{\rm{T}}} \right]} = {{0}_{N \times r}}$
|
(22)
|
由于 ${{{V}}_{\rm{S}}}$ 和 ${{V}}_{\rm{S}}^{\rm{T}}$ 均为酉矩阵,其列向量 ${{v}}_i,$ $i = 1,2,\cdots ,r$ 满足
|
${{v}}_i^{\rm{H}}{{v}}_j^{} = \delta (i - j) = \left\{ \!\! \begin{array}{l}
1,\quad \;{\rm{ }}i = j\\
0,\quad \;{\rm{ }}i \ne j
\end{array} \right.$
|
(23)
|
|
${{v}}_i^{\rm{T}}{{v}}_j^{} = \delta (i - j) = \left\{ \!\! \begin{array}{l}
1,\quad \;{\rm{ }}i = j\\
0,\quad \;{\rm{ }}i \ne j
\end{array} \right.$
|
(24)
|
其中, $\delta ( \cdot )$ 表示Kronecker Delta函数。利用该特性,在式(22)两端分别右乘 ${{v}}_i^{},i = 1,2,\cdots ,r ,得
|
$\left\{ \begin{array}{l}
\sum\limits_{i = 1}^r {{\sigma _i}\left[{{{{u}}_i}{{v}}_i^{\rm{H}} - ({{Ju}}_i^ * ){{v}}_i^{\rm{T}}} \right]} {{v}}_1^{} = {{{0}}_{N \times 1}}\\
\sum\limits_{i = 1}^r {{\sigma _i}\left[{{{{u}}_i}{{v}}_i^{\rm{H}} - ({{Ju}}_i^ * ){{v}}_i^{\rm{T}}} \right]} {{v}}_2^{} = {{{0}}_{N \times 1}}\\
\hspace{5pt} \vdots \\
\sum\limits_{i = 1}^r {{\sigma _i}\left[{{{{u}}_i}{{v}}_i^{\rm{H}} - ({{Ju}}_i^ * ){{v}}_i^{\rm{T}}} \right]} {{v}}_r^{} = {{{0}}_{N \times 1}}
\end{array} \right.$
|
(25)
|
进一步,可以得到
|
${{{u}}_i} = {{Ju}}_i^ * ,\quad i = 1,2,\cdots ,r$
|
(26)
|
因此, ${{{U}}_{\rm{S}}}$ 的 $r$ 个列向量 ${{{u}}_i},i = 1,2,\cdots ,r$ 均具有斜对称结构,即 ${{{U}}_{\rm{S}}}$ 满足 ${{{U}}_{\rm{S}}} = {{JU}}_{\rm{S}}^ * $。 证毕
3.2 一步GLRT检测器设计
在斜对称约束下,采用一步GLRT研究部分均匀杂波中FOG目标的自适应检测问题。首先定义以下两个矩阵[24]:
|
${{{T}}_{{\rm{p0}}}} = {{{R}}_{\rm{p}}}{{R}}_{\rm{p}}^{\rm{H}}\hspace{90pt}$
|
(27)
|
|
${{{T}}_{{\rm{p1}}}} = ({{{R}}_{\rm{p}}} - {{{U}}_{\rm{S}}}{{{b}}_{\rm{p}}}){({{{R}}_{\rm{p}}} - {{{U}}_{\rm{S}}}{{{b}}_{\rm{p}}})^{\rm{H}}}$
|
(28)
|
其中
|
${{{R}}_{\rm{p}}} = [{{{z}}_{\rm{e}}},{{{z}}_{\rm{o}}}],{\rm{ }}{{{z}}_{\rm{e}}} = \frac{1}{2}({{z}} + {{J}}{{{z}}^ * }),{\rm{ }}{{{z}}_{\rm{o}}} = \frac{1}{2}({{z}} - {{J}}{{{z}}^ * })$
|
(29)
|
|
${{{b}}_{\rm{p}}} = [{{{b}}_{\rm{e}}},{{{b}}_{\rm{o}}}],{\rm{ }}{{{b}}_{\rm{e}}} = \frac{1}{2}({{b}} + {{J}}{{{b}}^ * }),{\rm{ }}{{{b}}_{\rm{o}}} = \frac{1}{2}({{b}} - {{J}}{{{b}}^ * })$
|
(30)
|
|
${{{S}}_{\rm{p}}} = \frac{1}{2}({{S}} + {{J}}{{{S}}^ * }{{J}})\hspace{122pt}$
|
(31)
|
则
T0和
T1可以表示为:
|
${{{T}}_0} = \frac{1}{2}({{{T}}_0} + {{JT}}_0^ * {{J}}) = {{{T}}_{{\rm{p0}}}} + \frac{1}{\gamma }{{{S}}_{\rm{p}}}$
|
(32)
|
|
${{{T}}_1} = \frac{1}{2}({{{T}}_1} + {{JT}}_1^ * {{J}}) = {{{T}}_{{\rm{p1}}}} + \frac{1}{\gamma }{{{S}}_{\rm{p}}}$
|
(33)
|
分别代入
f0和
f1,则GLRT可表示为:
|
$\frac{{\begin{array}{*{20}{c}}
{\max } \\
{{\mathbf{M}} \in {{\mathbf{M}}_{\text{P}}}}
\end{array}\begin{array}{*{20}{c}}
{\max } \\
{{{\mathbf{b}}_{\text{p}}}}
\end{array}\begin{array}{*{20}{c}}
{\max } \\
\gamma
\end{array}\frac{{{\text{etr}}\left[ { - {{\mathbf{M}}^{ - 1}}\left( {{{\mathbf{T}}_{{\text{p1}}}} + \frac{1}{\gamma }{{\mathbf{S}}_{\text{p}}}} \right)} \right]}}{{{\gamma ^{NK}}{{\left[ {\det ({\mathbf{M}})} \right]}^{K + 1}}}}}}{{\begin{array}{*{20}{c}}
{\max } \\
{{\mathbf{M}} \in {{\mathbf{M}}_{\text{P}}}}
\end{array}\begin{array}{*{20}{c}}
{\max } \\
\gamma
\end{array}\frac{{{\text{etr}}\left[ { - {{\mathbf{M}}^{ - 1}}\left( {{{\mathbf{T}}_{{\text{p0}}}} + \frac{1}{\gamma }{{\mathbf{S}}_{\text{p}}}} \right)} \right]}}{{{\gamma ^{NK}}{{\left[ {\det ({\mathbf{M}})} \right]}^{K + 1}}}}}}\mathop {\mathop > \limits_ < }\limits_{{{\text{H}}_0}}^{{{\text{H}}_{\text{1}}}} G$
|
(34)
|
在斜对称约束下,H0和H1条件下协方差矩阵的最大似然估计分别为$\widehat{{{M}}}_0 = {{{T}}_{{\rm{p0}}}} + \frac{1}{\gamma }{{{S}}_{\rm{p}}}$ 和 $\widehat{{{M}}}_1 = {{{T}}_{{\rm{p1}}}} + \frac{1}{\gamma }{{{S}}_{\rm{p}}}$ [24],代入GLRT,得
|
${{{{\min }\atop \gamma} \left[ {{\gamma ^{NK/(K + 1)}} \ \det \left( {{T_{{\rm{p0}}}} + {1 \over \gamma }{S_{\rm{p}}}} \right)} \right]} \over {{{\min }\atop \gamma} \left[ {{\gamma ^{NK/(K + 1)}} \ \mathop {\min }\limits_{{b_{\rm{p}}}} \det \left( {{T_{{\rm{p1}}}} + {1 \over \gamma }{S_{\rm{p}}}} \right)} \right]}}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} G$
|
(35)
|
在H
1条件下,首先计算
bp的估计值,即
|
$\begin{aligned}
{{{\bf{\widehat {b}}}}_{\rm{p}}} = & \mathop {\arg \min }\limits_{{{\bf{{b}}}_{\rm{p}}}} \det \left( {{{\bf{{T}}}_{{\rm{p1}}}} + \frac{1}{\gamma }{{\bf{{S}}}_{\rm{p}}}} \right)\\
= & \mathop {\arg \min }\limits_{{{\bf{{b}}}_{\rm{p}}}} \det \bigg[{({{\bf{{R}}}_{\rm{p}}} - {{\bf{{U}}}_{\rm{S}}}{{\bf{{b}}}_{\rm{p}}}){{({{\bf{{R}}}_{\rm{p}}} - {{\bf{{U}}}_{\rm{S}}}{{\bf{{b}}}_{\rm{p}}})}^{\rm{H}}}} \\
& + \left. { \frac{1}{\gamma }{{\bf{{S}}}_{\rm{p}}}} \right]
\end{aligned}$
|
(36)
|
关于
bp求偏导,得到其估计值为:
|
$\widehat{{{b}}}_{\rm{p}} = {({{U}}_{\rm{S}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{{U}}_{\rm{S}}})^{ - 1}}{{U}}_{\rm{S}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{{R}}_{\rm{p}}}$
|
(37)
|
在计算时,利用了式(38)
[23]
|
$\begin{array}{l}
\det \left[{({{{R}}_{\rm{p}}} - {{{U}}_{\rm{S}}}{{{b}}_{\rm{p}}}){{({{{R}}_{\rm{p}}} - {{{U}}_{\rm{S}}}{{{b}}_{\rm{p}}})}^{\rm{H}}} + \frac{1}{\gamma }{{{S}}_{\rm{p}}}} \right]\\
= \frac{1}{{{\gamma ^N}}} \det ({{{S}}_{\rm{p}}}) \\
\quad \cdot \det \left[{\gamma {{({{{R}}_{\rm{p}}} - {{{U}}_{\rm{S}}}{{{b}}_{\rm{p}}})}^{\rm{H}}}{{S}}_{\rm{p}}^{ - 1} ({{{R}}_{\rm{p}}} - {{{U}}_{\rm{S}}}{{{b}}_{\rm{p}}}) + {{{I}}_{2 \times 2}}} \right]\hspace{70pt}
\end{array}$
|
(38)
|
将 $\widehat{{{b}}}_{\rm{p}}$ 代入GLRT,得
|
$\frac{{{{\min }\atop \gamma} \left[{{\gamma ^{NK/(K + 1)}} \det \left( {{{\widehat{{{T}}}}_{{\rm{p0}}}} + \frac{{1}}{{\gamma} }{{{S}}_{\rm{p}}}} \right)} \right]}}{{{{\min }\atop \gamma} \left[{{\gamma ^{NK/(K + 1)}}\det \left( {{{\widehat{{{T}}}}_{{\rm{p1}}}} + \frac{{1}}{{\gamma} }{{{S}}_{\rm{p}}}} \right)} \right]}}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} G$
|
(39)
|
其中
|
$\left. \begin{array}{l}
{{\widehat{{{T}}}}_{{\rm{p0}}}} = {{{T}}_{{\rm{p0}}}}\\
{{\widehat{{{T}}}}_{{\rm{p1}}}} = \left[{{{{R}}_{\rm{p}}} - {{{U}}_{\rm{S}}}{{({{U}}_{\rm{S}}^{\rm{H}}{{S}}_{\rm{p}}^{ - {\rm{1}}}{{{U}}_{\rm{S}}})}^{ - 1}}{{U}}_{\rm{S}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{{R}}_{\rm{p}}}} \right]\\
\quad\quad\quad \cdot {\left[{{{{R}}_{\rm{p}}} - {{{U}}_{\rm{S}}}{{({{U}}_{\rm{S}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{{U}}_{\rm{S}}})}^{ - 1}}{{U}}_{\rm{S}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{{R}}_{\rm{p}}}} \right]^{\rm{H}}}
\end{array} \right\}$
|
(40)
|
由文献
[38]的定理可知,当 $\gamma$ 取以下方程的唯一正数解时,分母和分子取最小值,即
|
$\sum\limits_{i = 1}^r {\frac{{{\lambda _i}\gamma }}{{{\lambda _i}\gamma + 1}}} = \frac{N}{{K + 1}}$
|
(41)
|
其中,在H0条件下, ${\lambda _i}$ 表示矩阵 ${{S}}_{\rm{p}}^{ - 1/2}{{\widehat{{{T}}}}_{{\rm{p0}}}}{{S}}_{\rm{p}}^{ - 1/2}$ 的非零特征值,在H1条件下, ${\lambda _i}$ 表示矩阵 ${{S}}_{\rm{p}}^{ - 1/2} {{\widehat{{{T}}}}_{{\rm{p1}}}}$ $\cdot {{S}}_{\rm{p}}^{ - 1/2}$ 的非零特征值。
利用该定理,一步GLRT最终表示为:
|
${{\hat \gamma _0^{NK/(K + 1)}\det \left( {{{\widehat T}_{{\rm{p0}}}} + {1 \over {{\rm{ }}{{\hat \gamma }_0}}}{S_{\rm{p}}}} \right)} \over {\hat \gamma _1^{NK/(K + 1)}\det \left( {{{\widehat T}_{{\rm{p1}}}} + {1 \over {{\rm{ }}{{\hat \gamma }_1}}}{S_{\rm{p}}}} \right)}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} G$
|
(42)
|
实际上,再次利用式(38),可以将一步GLRT等价表示为:
|
$${{{{({{\hat \gamma }_0})}^{ - {\rm{ }}{N \over {K + 1}}}}\det ({{\hat \gamma }_0}{Φ _0} + I)} \over {{{({{\hat \gamma }_1})}^{ - {\rm{ }}{N \over {K + 1}}}}\det ({{\hat \gamma }_1}{Φ _1} + I)}}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} G$$
|
(43)
|
其中
|
$\quad {{{Φ}} _0} = {{ {R}}}_{\rm{p}}^{\rm{H}}{{ {S}}}_{\rm{p}}^{ - 1}{{{ {R}}}_{\rm{p}}} \hspace{96pt}$
|
(44)
|
|
${{Φ} _1} = {{R}}_{\rm{p}}^{\rm{H}}({{ {S}}}_{\rm{p}}^{ - 1} - {{{Θ}} _{\rm{p}}}){{{ {R}}}_{\rm{p}}}\hspace{53pt}$
|
(45)
|
|
${Θ} _{\rm{p}} = {{S}}_{\rm{p}}^{ - 1}{{{U}}_{\rm{S}}}{({{U}}_{\rm{S}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{{U}}_{\rm{S}}})^{ - 1}}{{U}}_{\rm{S}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}$
|
(46)
|
${\gamma _0}$ 和 ${\gamma _1}$ 的估计值分别为
[24]:
|
${\hat \gamma _0} = {{\sqrt {{\eta ^2}{\rm{t}}{{\rm{r}}^2}({\rm{}}{{\rm{Φ }}_0}) + 4N(2\eta + N - 4)\det ({\rm{}}{{\rm{Φ }}_0}} \ \ ) - \eta {\rm{tr}}({\rm{}}{{\rm{Φ }}_0})} \over {2(2\eta + N)\det ({\rm{}}{{\rm{Φ}}_0} \ )}}$
|
(47)
|
|
${\widehat \gamma _1} = \frac{{\sqrt {{\eta ^2}{\rm{t}}{{\rm{r}}^2}({{Φ} _1}) + 4N(2\eta + N - 4)\det ({{Φ} _1} \ )} \ - \eta {\rm{tr}}({{Φ} _1})}}{{2(2\eta + N)\det ({{Φ} _1})}}$
|
(48)
|
|
$\eta = K + 1 - N \hspace{148pt}$
|
(49)
|
在均匀杂波中, $\gamma = 1$ ,一步GLRT可简化为:
|
${{\det ({\rm{}}{{\rm{Φ }}_0} + I)} \over {\det ({\rm{}}{{\rm{Φ }}_1} + I)}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} G$
|
(50)
|
由于检测器设计时利用了杂波协方差矩阵和目标模型的斜对称结构,因此称之为P-GLRT检测器。
检测单元的杂波协方差矩阵通常是未知的,需要利用参考单元数据估计并替换,从而得到自适应检测器。在仅考虑协方差矩阵Hermitian结构的情况下,其最大似然估计即为采样协方差矩阵(Sample Covariance Matrix,SCM),即
|
${\widehat{{{M}}}} = \frac{1}{K}\sum\limits_{k = 1}^K {{{\mathbf{z}}_k}{\mathbf{z}}_k^{\text{H}}} = \frac{1}{K}{\mathbf{S}}$
|
(51)
|
若进一步考虑协方差矩阵的斜对称结构,则其最大似然估计为
[18]:
|
${\widehat{{{M}}}_p} = \frac{1}{2}(\widehat{{{M}}}+ {{J}}{\widehat{{{M}}}^ * }{{J}})$
|
(52)
|
这里称之为斜对称采样协方差矩阵(Persymmetric SCM,P-SCM)。将P-GLRT中的协方差矩阵 ${{S}}_{\rm{p}}^{}$ 替换为 ${\widehat{{{M}}}_{\rm{p}}}$ ,得到自适应P-GLRT检测器。在均匀和部分均匀杂波中,自适应P-GLRT检测器分别表示为:
|
${{\det ({{{\rm{\hat Φ}}}_0}/K + I)} \over {\det ({{{\rm{\hat Φ}}}_1}/K + I)}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}G $
|
(53)
|
|
${{{{(\hat \gamma {\mkern 1mu} _0^\prime )}^{ - {N \over {K + 1}}}}\det \left( {{{\hat \gamma {\mkern 1mu} _0^\prime } \over K}{{\widehat {{\rm{Φ }}}}_0} + I} \right)} \over {{{(\hat \gamma {\mkern 1mu} _1^\prime )}^{ - {N \over {K + 1}}}}\det \left( {{{\hat \gamma {\mkern 1mu} _1^\prime } \over K}{{\widehat {{\rm{Φ }}}}_1} + I} \right)}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}G$
|
(54)
|
其中,将式(44)-式(48)中的 ${{{S}}}_{\rm{p}}^{}$ 均替换为 ${\widehat{{{M}}}_{\rm{p}}}$ ,即为式(53)和式(54)中的$\widehat \gamma\,_0^{{\prime} }$ , $\widehat \gamma\,_1^{{\prime} }$ , ${\widehat {Φ} _0}$ 和 ${\widehat {Φ} _1}$ 。
若不考虑斜对称结构,则在均匀杂波中,一步GLRT检测器为[4, 39]:
|
$\frac{{{{{z}}^{\rm{H}}}\widehat {Θ} {{z}}}} {{1 + { \frac{1}{{K}}}{ {{{z}}^{\rm{H}}} {{\widehat{{{M}}}}^{ - 1}}{{z}} } }} {\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}G$
|
(55)
|
在部分均匀杂波中,一步GLRT即为ACE,检测器结构为
[4, 40]:
|
$\frac{{{{{z}}^{\rm{H}}}\widehat {Θ} {{z}}}}{{{{{z}}^{\rm{H}}}{{\widehat{{{M}}}}^{ - 1}}{{z}}}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}G$
|
(56)
|
其中
|
$\widehat {Θ} = {\widehat{{{M}}}^{ - 1}}{{{U}}_{\rm{S}}}{({{U}}_{\rm{S}}^{\rm{H}}{\widehat{{{M}}}^{ - 1}}{{{U}}_{\rm{S}}})^{ - 1}}{{U}}_{\rm{S}}^{\rm{H}}{\widehat{{{M}}}^{ - 1}}$
|
(57)
|
3.3 两步GLRT检测器设计
在两步法中,假定杂波协方差矩阵M已知(对应均匀杂波)或者协方差矩阵结构Σ已知(对应部分均匀杂波),对于后者,检测单元的协方差矩阵表示为M = $\kappa$ Σ,其中 $\kappa$ 表示M的首个对角线元素,与杂波的功率水平有关[38]。首先利用检测单元数据推导GLRT检测器,然后利用参考单元数据估计协方差矩阵并代入GLRT,得到自适应检测器。
(1) GLRT的推导
在均匀杂波中,检测单元观测数据在H0和H1假设下的PDF分别为:
|
$f({{z}}|{{T}},{{\rm{H}}_0}) = \frac{1}{{{{π} ^N}\det ({{M}})}}{\rm{etr(}} - {{{M}}^{ - 1}}{{{T}}_{{\rm{p0}}}}{\rm{)}} \hspace{15pt}$
|
(58)
|
|
$f({{z}}|{{M}},{{{b}}_{\rm{p}}}{\rm{,}} \,{{\rm{H}}_1}) = \frac{1}{{{{π} ^N}\det ({{M}})}}{\rm{etr(}} - {{{M}}^{ - 1}}{{{T}}_{{\rm{p1}}}}{\rm{)}}$
|
(59)
|
GLRT可表示为:
|
${{{{\max } \atop {b_{\rm{p}}}} \ f(z|M,{b_{\rm{p}}},{{\rm{H}}_1})} \over {f(z|M,{{\rm{H}}_0})}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}{G_0}$
|
(60)
|
首先估计
bp,使分子最大化,其估计值为:
|
$\widehat{{{b}}}_{\rm{p}} = {({{U}}_{\rm{S}}^{\rm{H}}{{{M}}^{ - 1}}{{{U}}_{\rm{S}}})^{ - 1}}{{U}}_{\rm{S}}^{\rm{H}}{{{M}}^{ - 1}}{{{R}}_{\rm{p}}}$
|
(61)
|
将 $\widehat{{{ b}}}_{\rm{p}}$ 代入GLRT,并在两边取对数,得
|
$${\rm{tr}}\left[ {R_{\rm{p}}^{\rm{H}}{M^{ - 1}}{U_{\rm{S}}}{{(U_{\rm{S}}^{\rm{H}}{M^{ - 1}}{U_{\rm{S}}})}^{ - 1}}U_{\rm{S}}^{\rm{H}}{M^{ - 1}}{R_{\rm{p}}}} \right]\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} {G_0}$$
|
(62)
|
定义以下投影矩阵:
|
${{{P}}_{{{{M}}^{ - 1/2}} \ \ {{{U}}_{\rm{S}}}}} = {{{M}}^{ - 1/2}}{{{U}}_{\rm{S}}}{({{U}}_{\rm{S}}^{\rm{H}}{{{M}}^{ - 1}}{{{U}}_{\rm{S}}})^{ - 1}}{{U}}_{\rm{S}}^{\rm{H}}{{{M}}^{ - 1/2}}$
|
(63)
|
它表示白化后向目标子空间的正交投影算子,令 ${{Q}} = {{{Q}}^{ - 1/2}}{{{P}}_{{{{M}}^{ - 1/2}} \ \ {{{U}}_{\rm{S}}}}}{{{M}}^{ - 1/2}}$ ,则GLRT最终表示为:
|
${\rm{tr(}}{{R}}_{\rm{p}}^{\rm{H}}{{Q}}{{{R}}_{\rm{p}}}{\rm{)}}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} {G_0}$
|
(64)
|
在部分均匀杂波中,检测单元观测数据在H0和H1假设下的PDF分别为:
|
${f(z|\kappa ,\Sigma ,{{\rm{H}}_0}) = {1 \over {{{(\pi \kappa )}^N}\det (\Sigma )}}{\rm{etr}}\left( { - {{{\Sigma ^{ - 1}} \ \ {T_{{\rm{p0}}}}} \over \kappa }} \right){\rm{ }}}$
|
(65)
|
|
$f(z|\kappa ,\Sigma ,{b_{\rm{p}}},{{\rm{H}}_1}) = {1 \over {{{(\pi \kappa )}^N}\det (\Sigma )}}{\rm{etr}}\left( { - {{{\Sigma ^{ - 1}} \ \ {T_{{\rm{p1}}}}} \over \kappa }} \right)$
|
(66)
|
GLRT可表示为:
|
${{{\max \atop {b_{\rm{p}}}}{{\max} \atop \kappa} f(z|\kappa ,\Sigma ,{b_{\rm{p}}},{{\rm{H}}_1})} \over {{{\max} \atop \kappa} f(z|\kappa ,\Sigma ,{{\rm{H}}_0})}}\mathop {\mathop > \limits_ \lt }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} {G_0}$
|
(67)
|
在H
0和H
1条件下, $\kappa $ 的估计值分别为:
|
${\widehat \kappa _0} = \frac{{{\rm{tr}}({{Σ} ^{ - 1}}{{{T}}_{{\rm{p0}}}})}}{N}$
|
(68)
|
|
${\widehat \kappa _1} = \frac{{{\rm{tr}}({{Σ} ^{ - 1}}{{{T}}_{{\rm{p1}}}})}}{N}$
|
(69)
|
代入GLRT,得
|
${{{\rm{tr}}({\Sigma ^{ - 1}}{T_{{\rm{p0}}}})} \over {{\min \atop {b_{\rm{p}}}} {\rm{tr}}({\Sigma ^{ - 1}}{T_{{\rm{p1}}}})}}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} {G_0}$
|
(70)
|
bp的估计值为:
|
$\widehat{{{b}}}_{\rm{p}} = {({{U}}_{\rm{S}}^{\rm{H}}{{Σ} ^{ - 1}}{{{U}}_{\rm{S}}})^{ - 1}}{{U}}_{\rm{S}}^{\rm{H}}{{Σ} ^{ - 1}}{{{R}}_{\rm{p}}}$
|
(71)
|
代入上式并化简,得
|
$\frac{{{\text{tr}}\left[ {{{R}}_{\text{p}}^{\text{H}}{{\Sigma }^{ - 1}}{{{U}}_{\text{S}}}{{({{U}}_{\text{S}}^{\text{H}}{\Sigma ^{ - 1}}{{{U}}_{\text{S}}})}^{ - 1}}{{U}}_{\text{S}}^{\text{H}}{{\Sigma }^{ - 1}}{{{R}}_{\text{p}}}} \right]}}{{{\text{tr}}({{R}}_{\text{p}}^{\text{H}}{{\Sigma }^{ - 1}}{{{R}}_{\text{p}}})}}\mathop {\mathop > \limits_ < }\limits_{{{\text{H}}_0}}^{{{\text{H}}_{\text{1}}}} {G_0}$
|
(72)
|
令
|
${Ψ} = {{Σ} ^{ - 1}}{{{U}}_{\rm{S}}}{({{U}}_{\rm{S}}^{\rm{H}}{{Σ} ^{ - 1}}{{{U}}_{\rm{S}}})^{ - 1}}{{U}}_{\rm{S}}^{\rm{H}}{{Σ} ^{ - 1}}$
|
(73)
|
则GLRT可最终表示为:
|
${{{\rm{tr}}(R_{\rm{p}}^{\rm{H}}{Ψ} {R_{\rm{p}}})} \over {{\rm{tr}}(R_{\rm{p}}^{\rm{H}}{\Sigma ^{ - 1}}{R_{\rm{p}}})}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}{G_0}$
|
(74)
|
(2) 协方差矩阵的估计
在均匀和部分均匀杂波中,分别将检测器中的协方差矩阵 ${M}$ 和 ${Σ} $ 替换为估计值$\widehat{{{M}}}_{\rm{p}}$ ,得到自适应检测器,分别称之为斜对称AMF(Persymmetric AMF,P-AMF)和斜对称ACE(Persymmetric ACE,P-ACE),即
|
${\rm{tr(}}{{R}}_{\rm{p}}^{\rm{H}}{\widehat {Θ} _{\rm{p}}}{{{R}}_{\rm{p}}}{\rm{)}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}{G_0}$
|
(75)
|
|
${{{\rm{tr}}(R_{\rm{p}}^{\rm{H}}{{\widehat {Θ}}_{\rm{p}}}{R_{\rm{p}}})} \over {{\rm{tr}}(R_{\rm{p}}^{\rm{H}}\widehat M_{\rm{p}}^{ - 1}{R_{\rm{p}}})}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}{G_0}$
|
(76)
|
在不考虑斜对称结构的情况下,均匀杂波和部分均匀杂波中子空间目标的两步GLRT检测器分别称为AMF[41]和ACE[4],即
|
${{{z}}^{\rm{H}}}\widehat {Θ} {{z}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}{G_0}$
|
(77)
|
|
${{{z^{\rm{H}}}\widehat {Θ}z} \over {{z^{\rm{H}}}{{\widehat M}^{ - 1}}z}}{\rm{ }}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}}{G_0}$
|
(78)
|
3.4 检测器的总结
为便于检测性能分析,在表 1中,将建立在GLRT和P-GLRT(包括一步法和两步法)基础上的自适应子空间检测器进行了汇总。可以看出,在考虑斜对称的情况下,均匀杂波和部分均匀杂波中基于一步法和两步法设计的检测器具有彼此不同的形式。而在不考虑斜对称的情况下,部分均匀杂波中基于一步法和两步法设计的检测器完全相同,均称为ACE,或CFAR ASD,均匀杂波中采用一步法设计的检测器(即GLRT检测器)要比两步法检测器(即AMF检测器)复杂。在均匀杂波中,斜对称检测器关于协方差矩阵具有CFAR特性,而在部分均匀杂波中,斜对称检测器关于协方差矩阵和尺度变换均具有CFAR特性,具体证明过程与文献[23]给出的方法类似,这里不再详细说明。若要进一步计算检测概率和虚警概率的理论表达式,还需要对检测统计量进行等价统计分解,将其表示为独立随机变量构成的简单函数。
表 1(Tab. 1)
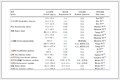
表 1 自适应子空间检测器总结Tab. 1 Summary of adaptive subspace detectors
| 检测器 |
杂波模型 |
| 均匀杂波 |
部分均匀杂波 |
| 一步法 |
GLRT |
式(55) |
式(56) |
| P-GLRT |
式(53) |
式(54) |
| 两步法 |
GLRT |
式(77) |
式(78) |
| P-GLRT |
式(75) |
式(76) |
|
表 1 自适应子空间检测器总结
Tab. 1 Summary of adaptive subspace detectors |
当多维子空间目标退化为秩1目标时,式(44),式(45)以及式(47),式(48)分别等价为:
|
${\widetilde {Φ} _0} = {{R}}_{\rm{p}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{{R}}_{\rm{p}}} \hspace{170pt}$
|
(79)
|
|
${\widetilde {Φ} _1} = {{R}}_{\rm{p}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{{R}}_{\rm{p}}} - \frac{{{{R}}_{\rm{p}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{p}}{{{p}}^{\rm{H}}}{{S}}_{\rm{p}}^{ - 1}{{{R}}_{\rm{p}}}}}{{{{{p}}^{\rm{H}}}{{S}}_{\rm{p}}^{ - 1}{{p}}}} \hspace{80pt}$
|
(80)
|
|
${{\mathop {\hat \gamma }\limits^ \sim}_0} = {{\sqrt {{\eta ^2}{\rm{t}}{{\rm{r}}^2}({{\tilde \Phi }_0}) + 4N(2\eta + N - 4)\det ({{\tilde \Phi }_0} )} \ - \eta {\rm{tr}}({{\tilde \Phi }_0})} \over {2(2\eta + N)\det ({{\tilde \Phi }_0})}}$
|
(81)
|
|
${{\mathop {\hat \gamma }\limits^ \sim}_1} = {{\sqrt {{\eta ^2}{\rm{t}}{{\rm{r}}^2}({{\tilde \Phi }_1}) + 4N(2\eta + N - 4)\det ({{\tilde \Phi }_1})} \ - \eta {\rm{tr}}({{\tilde \Phi }_1})} \over {2(2\eta + N)\det ({{\tilde \Phi }_1})}}$
|
(82)
|
将以上各式分别代入一步GLRT检测器,其中,在部分均匀杂波中,GLRT可表示为
[24]:
|
${{{{({{\mathop {\hat \gamma }\limits^ \sim}_0})}^{ - {\rm{ }}{N \over {K + 1}}}}\det ({{\mathop {\hat \gamma }\limits^ \sim}_0}{{\tilde \Phi }_0} + I)} \over {{{({{\mathop {\hat \gamma }\limits^ \sim}_1})}^{ - {N \over {K + 1}}}}\det ({{\mathop {\hat \gamma }\limits^ \sim}_1}{{\tilde \Phi }_1} + I)}}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} \tilde G$
|
(83)
|
在均匀杂波中,由于
|
${{\det ({{\tilde \Phi }_0} + I)} \over {\det ({{\tilde \Phi }_1} + I)}} = {1 \over {\det \left[ {I - {\Xi ^{ - 1/2}} \ \ {{R_ \ {\rm{p}}^{\rm{H}} \ S_{\rm{p}}^{ - 1}p{p^{\rm{H}}}S_{\rm{p}}^{ - 1} \ {R_ \ {\rm{p}}}} \over {{p^{\rm{H}}}S_{\rm{p}}^{ - 1}p}}{\Xi ^{ - 1/2}}} \ \ \right]}} \\
\qquad \qquad = {1 \over {1 - {{{p^{\rm{H}}}S_ \ {\rm{p}}^{ - 1} \ {R_{\rm{p}}}{\Xi ^{ - 1}} \ R_ \ {\rm{p}}^{\rm{H}}S_{\rm{p}}^{ - 1}p} \over {{p^{\rm{H}}}S_{\rm{p}}^{ - 1}p}}}}$
|
(84)
|
因此,GLRT可简化为
[23]:
|
${{{p^{\rm{H}}}S_{\rm{p}}^{ - 1}{R_{\rm{p}}}{\Xi ^{ - 1}}R_{\rm{p}}^{\rm{H}}S_{\rm{p}}^{ - 1}p} \over {{p^{\rm{H}}}S_{\rm{p}}^{ - 1}p}}\mathop {\mathop > \limits_ < }\limits_{{{\rm{H}}_0}}^{{{\rm{H}}_{\rm{1}}}} \tilde G$
|
(85)
|
其中
|
${Ξ} = {{R}}_{\rm{p}}^{\rm{H}}{{S}}_{\rm{p}}^{ - 1}{{{R}}_{\rm{p}}} + {{I}}$
|
(86)
|
由此可见,对于秩1目标,在均匀和部分均匀杂波中,本文设计的一步P-GLRT分别退化为式(83)和式(85),即文献
[23]和文献
[24]中的P-GLRT检测器。
4 性能分析
采用Monte Carlo仿真方法,对子空间目标的斜对称自适应检测器进行性能分析,并与未考虑斜对称结构的自适应检测器进行对比分析。虚警概率 ${P_{{\rm{fa}}}}$ 设定为10-3,检测阈值和检测概率 ${P_{\rm{d}}}$ 均采用Monte Carlo仿真计算。估计每一个 ${P_{{\rm{fa}}}}$ 和${P_{\rm{d}}}$ 的仿真次数分别为 $100/{P_{{\rm{fa}}}}$ 和 $100/{P_{\rm{d}}}$ 次。
假定杂波具有幂率衰减形式的相关函数,协方差矩阵M的第 $(i,j)$ 个元素为:
|
${[{{M}}]_{i,j}} = {\rho ^{|i - j|}}$
|
(87)
|
其中, $\rho$ 表示1阶相关系数,与该相关函数对应的杂波谱模型又称为洛伦兹(Lorentzian)谱
[42],仿真时取 $\rho = 0.9$ 。目标子空间的维数为
r = 2,导向矩阵
E完全已知,归一化多普勒频率分别为 ${f_{\rm{D}}} = 0.2$
和 ${f_{\rm{D}}} = 0.3$
,目标回波功率在子空间各维上均匀分布,且目标幅度矢量
a
中的各元素均设定为单位值。根据上述假设,信杂比(Signal-to-Clutter Ratio,SCR)定义为:
|
${\rm{SCR}} = {({{Ea}})^{\rm{H}}}{{{M}}^{ - 1}}({{Ea}})/N$
|
(88)
|
4.1 与已有检测器的性能比较
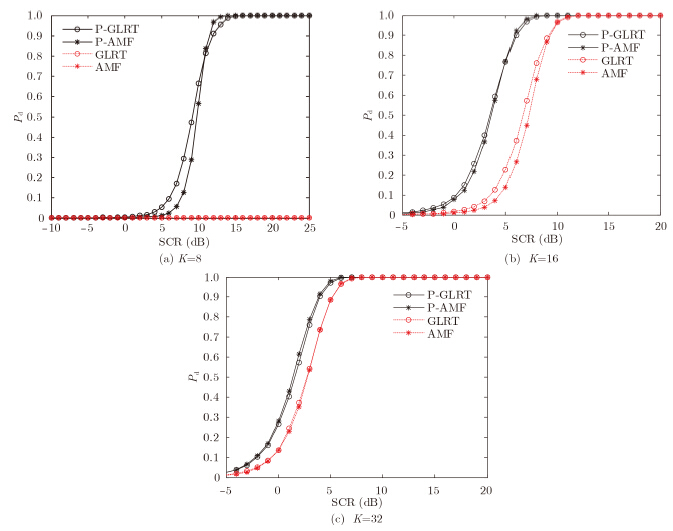
在性能比较时考虑均匀杂波背景,相干脉冲数为N = 8,参考单元数K为参数(K = 8,16,32)。对于不同的K,分析比较4类检测器的检测概率随SCR的变化情况,4类检测器分别为一步P-GLRT,P-AMF,一步GLRT和AMF,仿真结果分别如图 1(a),图 1(b),图 1(c)所示。
由图 1可知,在参考单元数相同时,一步P-GLRT和P-AMF在检测性能上均优于已有的一步GLRT和AMF。这是因为前两类检测器在设计时充分挖掘了协方差矩阵的结构信息,在保持相同检测性能的情况下可减小对参考单元数的需求。随着K的增加,与已有检测器的检测性能差异逐渐减小,其中,K=32时,对应检测器的检测性能已接近一致,例如,当 ${P_{\rm{d}}} = 0.9$ 时,一步GLRT和AMF与对应的斜对称检测器相比,检测性能损失均在1 dB以下。可见,当参考单元数较为充足时,利用协方差矩阵结构信息所带来的检测性能改善较小。
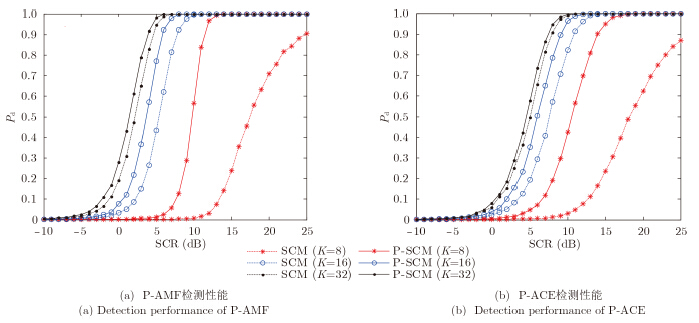
4.2 协方差矩阵估计方法的影响
在高斯杂波中,SCM为考虑Hermitian结构情况下协方差矩阵的最大似然估计,而P-SCM是在同时考虑Hermitian结构和斜对称结构时协方差矩阵的最大似然估计。分别将SCM和P-SCM代入检测器,并以P-AMF和P-ACE为例分析协方差矩阵估计方法对检测性能的影响,分析结果分别如图 2(a),图 2(b)所示。可以看出,以K 为参数,相比于SCM,协方差矩阵估计值采用P-SCM时,P-AMF和P-ACE均有一定的性能改善,但是改善程度随K 的增加而减小。这就表明,尽管P-AMF和P-ACE检测器在设计阶段考虑了斜对称结构,但是在检测器的自适应阶段若没有有效利用协方差矩阵的斜对称结构,仍然会出现一定的检测性能损失。
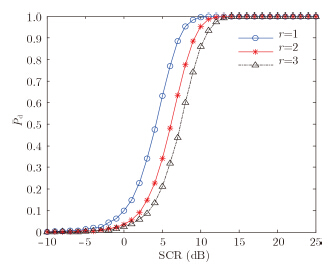
4.3 目标子空间维数的影响
以P-ACE检测器为研究对象,分析目标子空间维数r对检测性能的影响。取N=8,K=16,r为参数(r=1,2,3),协方差矩阵估计方法为P-SCM,检测性能曲线如图 3所示。由图 3可知,在SCR一定的情况下,r 越小,检测概率越大。实际上,目标的维数反应了目标信号所在线性子空间的维数,该线性子空间由观测空间张成,当r增加时,目标信号的不确定度也增加,与此同时,目标子空间与满秩的杂波子空间更加接近,目标能量有所泄露,增加了检测难度。因此,在达到相同检测概率的条件下,检测器对SCR的需求随r的增加而增大。对于P-AMF,可以得到类似的分析结果。
4.4 目标子空间失配性能分析
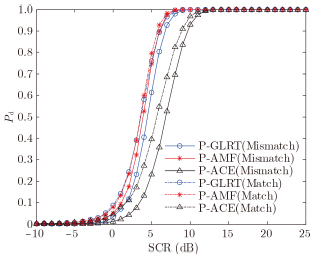
以P-GLRT,P-AMF和P-ACE为研究对象,分析目标子空间与假定模型失配情况下的检测性能。该部分的仿真场景与文献[36]中距离-多普勒扩展目标的失配性能分析类似,差别在于这里仅关注多普勒维的失配,即假定目标仅存在于一个距离单元,但是具有两个多普勒频点,归一化多普勒频率分别为fD=0.2和fD=0.3,而在检测阶段检测器并不是匹配于由这两个频点构成的导向矩阵,而是匹配于 ${f_{\rm{D}}} = 0.2$ 的情况。同样取 $N = 8$ , $K = 16 $ ,3类检测器在目标子空间匹配和失配情况下的检测性能曲线如图 4所示。由图 4可知,P-GLRT和P-ACE的检测性能损失相对来说较为显著,而P-AMF的检测性能在匹配和失配条件下变化不大,表明P-GLRT和P-ACE检测器对失配的敏感性强于P-AMF,这与1维情况下GLRT对导向矢量失配比较敏感的结论一致[43]。
4.5 目标起伏的影响
以上仿真中均假定目标的幅度非随机起伏,这里将考虑一种更加接近实际情况的仿真环境,即目标幅度 $\left| \alpha \right|$ 和相位在每次仿真时都随机起伏,其中相位起伏服从 $ ( - {π} ,{π} )$ 之间的均匀分布,而幅度起伏服从自由度为2m的 $\chi$ 分布,其PDF为[33]:
|
${f_{\left| \alpha \right|}}(x) = 2{\left( {\frac{m}{{\overline {{{\left| \alpha \right|}^2}} }}} \right)^m}\frac{{{x^{2m - 1}}}}{{\Gamma (m)}}\exp \left( { - \frac{m}{{\overline {{{\left| \alpha \right|}^2}} }}{x^2}} \right),\\
\quad\quad\quad\quad x > 0,\,\,m > 0$
|
(89)
|
其中, $\Gamma ( \cdot )$ 是Gamma函数,参数
m是目标幅度起伏程度的定量表征,取值越小,则目标的起伏程度越大,当
m=1时,目标幅度建模为瑞利分布,当
m取无穷大时,对应非随机起伏的情况。在目标起伏时,SCR定义为:
|
${\rm{SCR}} ={E}\left\{ {{{({{Ea}})}^{\rm{H}}}{{{M}}^{ - 1}}({{Ea}})} \right\} {\LARGE{ / }} N$
|
(90)
|
取
N=8,
K=16,
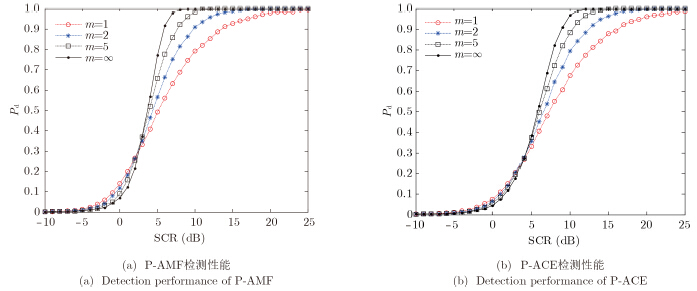
m为参数( $m = 1,2,5,\infty $ ),对于这4种不同起伏程度的子空间目标,P-AMF和P-ACE的检测性能曲线分别如
图 5(a),
图 5(b)所示。
可以看出,对于这两类检测器,当检测概率在较小的范围内变化时(比如 ${P_{\rm{d}}} \lt 0.4$ ),检测性能对目标起伏程度不敏感。当检测概率较大时,随着目标起伏程度的减弱,检测性能逐渐改善。对于 $m = 1$ 和$m = \infty$ 这两种极端情况,分别对应了最差和最好的检测性能[7],实际工作时的检测性能往往介于两者之间。当${P_{\rm{d}}} = 0.9$ 时,相比于非随机起伏目标,P-AMF和P-ACE在检测瑞利起伏目标时对SCR的需求分别增加约8 dB和7 dB,这也表明检测起伏目标的难度明显大于非起伏目标。
5 结束语
研究了斜对称约束下多维子空间目标的自适应检测问题。在均匀和部分均匀杂波中,分别采用一步和两步GLRT的基本原理,推导设计了4类斜对称自适应检测器,即均匀杂波中的一步P-GLRT,部分均匀杂波中的一步P-GLRT,P-AMF和P-ACE,并对其检测性能进行了仿真分析。上述检测器充分利用了协方差矩阵的结构信息,仿真结果表明,与已有检测器相比,在参考单元数不足时,斜对称检测器可明显改善检测性能。以P-SCM作为检测器中协方差矩阵的估计值,在检测性能上优于SCM估计方法。在检测概率相同时,检测器对SCR的需求随目标子空间维数的增加而增大。在目标模型失配条件下,P-GLRT和P-ACE的检测性能损失高于P-AMF。此外,对起伏目标的检测性能分析结果表明,随目标起伏程度的减弱,检测性能逐渐改善。
当雷达分辨率较高时,杂波背景将偏离高斯模型,在这种情况下,复合高斯模型得到了广泛应用,为此,下一步将重点研究复合高斯杂波中子空间目标的斜对称自适应检测问题。
 5)
5) 2)
2) 1)
1) 6)
6) 1)
1) 1)
1) 2)
2) 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 3)
3) 1)
1) 3)
3) 3)
3) 2)
2) 3)
3) 1)
1) 1)
1) 1)
1) 1)
1) 9)
9) 12)
12) 1)
1) 2)
2) 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 2)
2) 2)
2) 1)
1) 1)
1) 4)
4) 1)
1) 2)
2) 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 2015, Vol. 4 Issue (4): 418–430 DOI:
2015, Vol. 4 Issue (4): 418–430 DOI: 
