1 引言
在多通道自适应检测器设计阶段[1],需要确定噪声的协方差矩阵和有用信号的导向矢量(steering vector)。可以假定存在一定数量的、与待检测单元具有相同分布的参考数据用于估计噪声协方差矩阵[2, 3, 4, 5, 6],只要参考数据的个数超过信号维数的两倍,由噪声协方差矩阵未知引入的检测性能损耗是可以容忍的[7]。有用信号导向矢量可能存在不确定性。导致有用信号导向矢量失配的原因包括天线校准误差、波束指向误差、电磁波传播多径效应[8]等。在待检测数据中,还可能存在旁瓣干扰信号,其与有用信号的主要差异在于,有用信号的失配程度较小,而干扰的导向矢量失配程度较大。为此较为合理的检测器应该在保证对少许失配的有用信号的检测能力的前提下,还需要对失配程度较大的干扰信号有足够的抑制能力。
通常的自适应检测器对失配信号的检测能力是固定的,要么是稳健性(robust)的,要么选择性(selective)的,只是不同的检测器,其选择性或稳健性的程度有所差异。稳健性的检测器,如自适应匹配滤波器[9](Adaptive Match Filter,AMF),子空间检测器[10](Subspace Detector,SD),Wald检测器[11]等,这种类型的检测器对失配信号的检测能力受到失配程度的影响较小,即便信号存在较大的失配,检测概率仍然较高。选择性的检测器研究较多,如广义似然比检测器[12](Generalized Likelihood Ratio Test,GLRT),自适应相关估计器(Adaptive Coherent Estimator,ACE)[13],Rao检测器[14]等,这些检测器能够有效抑制失配程度较大的干扰信号。为了进一步提高对失配信号的选择性,Pulson给出了自适应波束形成正交抑制检验[15](Adaptive Beamformer Orthogonal Rejection Test,ABORT),以及Bandiera给出的选择性更强的白化ABORT[16](Whiten ABORT,W-ABORT),这些检测器的设计方法是在H0假设下引入一个虚假的信号,且该信号与有用信号正交。该检测器用于检测失配信号时,如果失配程度较大,即失配信号与导向矢量正交分量增大,导致检测结果更倾向选择H0假设,从而有效抑制了失配程度较大的信号。设计选择性检测器的另一种思路是假定待检测单元噪声协方差矩阵叠加有干扰分量,而参考数据协方差矩阵中不含干扰分量。这样在检测失配信号时,该信号可能被作为干扰信号而得到了抑制,从而提高了检测器的选择性。Bandiera进一步结合Rao检验的思路,设计了双归一化AMF(Double Normalized AMF,DN-AMF),研究表明,该检测器的选择性比W-ABORT更强[17]。
有用信号与干扰信号之间的差异主要集中在失配程度上,然而在实际应用过程中,有用信号和干扰信号的失配程度均较难在检测器设计阶段确定下来,因此有必要设计可调的检测器,即通过调整检测器的参数,改变检测器的选择性和稳健性。一种办法是假定有用信号约束在一个多维锥形区域内,对应检测器中的参数与锥形区域张角有关,通过凸优化的方法估计有用信号导向矢量,且一般而言没有闭合形式解,运算量比较大[18]。另一种办法就是采用参数化的方法[19],如采用双级(two stages)结构,将稳健性检测器和选择性检测器同时应用于失配信号的检测,只有当两个检测器同时判定信号存在时,才做出信号存在的判决,可以通过控制两个检测器的门限参数实现对检测性能的控制。也可以利用稳健性检测器与选择性检测器结构上的相似性[20],引入一个控制参数,通过调整该参数使得检测器的性能介于两种检测器性能之间。
本文考虑从检测器结构的相似性来设计可调检测器,这种途径关键是寻找对失配信号检测性能差异较大,但结构上具有相似性的两种检测器。AMF可以作为稳健型检测器,该检测器性能对信号的失配不敏感。而DN-AMF是一种敏感型检测器,根据文献[17]的结论,DN-AMF检测器性能对失配信号极为敏感,其敏感程度超过了RAO检测器和W-ABORT检测器。因此利用AMF和DN-AMF两种检测器结构上的相似性,构造出的可调检测器的性能可调范围将更大。为此在第2节给出了该检测器的结构,并在第3节分析了该检测器的检测性能。在第4节给出了数值仿真,深入分析了该检测器对失配信号的检测性能。最后给出了全文的结论。
2 可调自适应检测器
考虑如下二元假设检验问题:
|
$\eqalign{
& {{\rm{H}}_0}:{z} = {n} \cr
& {{\rm{H}}_1}:{z} = b{v} + {n} \cr} $
|
(1)
|
其中
n为维度为
N的零均值、正定协方差矩阵为
R的复高斯分布矢量。
N维复矢量
v为名义导向矢量(nominal steering vector),复数
b表示信号的幅度和电磁波传播效应。在上述假设检验问题中,假定参数
b和
R是未知的。同时还假定存在
K个仅包含噪声分量的参考数据
zk,
k=1,2,…,
K,这些参考数据与待检测数据中的噪声分量独立同分布。显然这是一个典型的点目标自适应检测问题
[12],如果采用双步GLRT方法
[9],即在构造检测器过程中,首先假定协方差矩阵
R是已知的,采用GLRT得到检验统计量,再利用
K个参考数据得到样本协方差矩阵代入到检验统计量中,可得到AMF检测器
[9]:
|
${t_{{\rm{AMF}}}} = {{{{\left| {{{v}^{\rm{H}}}{{S}^{ - 1}}{z}} \right|}^2}} \over {{{v}^{\rm{H}}}{{S}^{ - 1}}{v}}}$
|
(2)
|
如果假定待检测数据中的噪声分量中含有干扰分量,即待检测单元噪声协方差矩阵用R+qqH表示,其中q为N维未知复矢量,并采用Rao检测方法,可以获得DN-AMF检测器[17]:
|
${t_{{\rm{DN - AMF}}}} = {{{\beta ^2}{t_{{\rm{AMF}}}}} \over {\left( {1 - \beta } \right)\left( {1 - \beta + \beta {t_{{\rm{AMF}}}}} \right)}}$
|
(3)
|
其中:
|
$\beta = {1 \over {1 + {{z}^{\rm{H}}}{{S}^{ - 1}}{z} - {t_{{\rm{AMF}}}}}}$
|
(4)
|
利用上述两种检测器的结构上的相似性,可以得到一种可调检测器结构:
|
${t_t}\left( \gamma \right) = {\left( {{{\left( {{\beta ^{ - 1}} - 1} \right)}^{2\gamma }}t_{{\rm{AMF}}}^{ - 1} + {{\left( {{\beta ^{ - 1}} - 1} \right)}^\gamma }} \right)^{ - 1}}$
|
(5)
|
该检测器结构参数为
γ,若
γ=0,该检测器与AMF统计等价,若
γ=1,该检测器与DN-AMF等价。那么
γ的取值区间在0~1之间,就可以使得检测器的性能介于AMF与DN-AMF之间。需要指出的是,对于可调检测器,
γ取值甚至可以大于1。
3 检测器性能分析
根据自适应检测理论[10],[21]可知,AMF检测器可以表示为:
|
${t_{{\rm{AMF}}}} = {\beta ^{ - 1}}{t_K}$
|
(6)
|
其中
tk是广义似然比检验统计量
[12],其统计特性满足以
β为条件的、自由度为1和
K-
N+1的非中心复
F分布,非中心参数:
|
${\delta ^2} = {\rm{SNR}}\beta {\cos ^2}\theta $
|
(7)
|
其中信噪比SNR定义为:
|
${\rm{SNR}} = {\left| {b} \right|^2}{{v}^{\rm{H}}}{{R}^{ - 1}}{v}$
|
(8)
|
名义导向矢量
v与实际导向矢量
vm之间的夹角
θ用余弦平方定义为:
|
${\cos ^2}\theta = {{{{\left| {{{v}^{\rm{H}}}{{R}^{ - 1}}{{v}_m}} \right|}^2}} \over {\left( {{v}_m^{\rm{H}}{{R}^{ - 1}}{{v}_m}} \right)\left( {{{v}^{\rm{H}}}{{\bf{R}}^{ - 1}}{v}} \right)}}$
|
(9)
|
随机变量β满足参数为K-N+2和N-1的非中心贝塔分布,非中心参数:
|
$\delta _\beta ^2 = {\rm{SNR}}{\sin ^2}\theta $
|
(10)
|
需要指出的是,在H0假设条件下,tk和β是统计独立的。有了上述分析结论作为基础,可以对可调检测器的性能展开分析。检测概率可以表示为:
|
${P_{\rm{d}}} = {\rm{P}}\left\{ {{{\left( {{{\left( {{\beta ^{ - 1}} - 1} \right)}^{2\gamma }}\beta t_K^{ - 1} + {{\left( {{\beta ^{ - 1}} - 1} \right)}^\gamma }} \right)}^{ - 1}} > \eta , \\
\qquad \ \eta > 0;{{\rm{H}}_1}} \right\}$
|
(11)
|
其中
η为检测器门限,由此可以得到:
|
${P_{\rm{d}}} = {\rm{P}}\left\{ {{t_K} > {\eta _\beta },\beta > {1 \over {{\eta ^{ - 1/\gamma }} \ \ + 1}};{H_1}} \right\}$
|
(12)
|
其中
|
${\eta _\beta } = {{\eta \beta {{\left( {{\beta ^{ - 1}} - 1} \right)}^{2\gamma }}} \over {1 - \eta {{\left( {{\beta ^{ - 1}} - 1} \right)}^\gamma }}}$
|
(13)
|
由此可以得到:
|
${P_{\rm{d}}}\left( \gamma \right) = \int\limits_{{1 \over {{\eta ^{ - 1/\gamma }} \ \ + 1}}}^1 {\left( {1 - {P_{{\rm{cf}}}}\left( {{\eta _\beta }} \right)} \right)} {p_\beta }\left( \beta \right){\rm{d}}\beta $
|
(14)
|
其中
Pcf(.)表示自由度为1和
K-
N+1的非中心复
F分布的累积分布函数:
|
${P_{{\rm{cf}}}}\left( x \right) = {x \over {{{\left( {1 + x} \right)}^{K - N - 1}}}}\sum\limits_{k = 0}^{K - N} {\left( {\matrix{
{K - N + 1} \cr
{1 + k} \cr
} } \right){x^k} \\
\qquad \qquad \cdot \exp \left( { - {{{\delta ^2}} \over {1 + x}}} \right)\sum\limits_{i = 0}^k {{{\left( {{{{\delta ^2}} \over {1 + x}}} \right)}^i}{1 \over {i!}}} } $
|
(15)
|
pβ(
x)表示参数为
K-
N+2和
N-1的非中心贝塔分布的概率密度函数:
|
${p_\beta }\left( x \right) = \exp \left( { - \delta _\beta ^2x} \right)\sum\limits_{k = 0}^{K - N + 2} {\left( {\matrix{
{K - N + 2} \cr
k \cr
} } \right){{K!} \over {\left( {K + k} \right)!}}} \\
\qquad \qquad \cdot \delta _\beta ^{2k}{q_\beta }\left( {\beta ,K - N + 2,N + k - 1} \right)$
|
(16)
|
其中
qβ(
β,
m,
n)是参数为
m和
n的中心贝塔分布的概率密度函数:
|
${q_\beta }\left( {\beta ,m,n} \right) = {{\left( {n + m - 1} \right)!} \over {\left( {n - 1} \right)!\left( {m - 1} \right)}}{x^{m - 1}}{\left( {1 - x} \right)^{n - 1}}$
|
(17)
|
令SNR=0,可以得到虚警概率:
|
${P_{{\rm{fa}}}}\left( \gamma \right) = \int\limits_{{1 \over {{\eta ^{ - 1/\gamma }} \ \ + 1}}}^1 {{1 \over {{{\left( {1 + {\eta _\beta }} \right)}^{K - N + 1}}}} \\
\qquad \qquad \cdot {q_\beta }\left( {\beta ,K - N + 2,N - 1} \right){\rm{d}}\beta } $
|
(18)
|
4 计算机仿真分析
4.1 可调检测器性能分析
首先分析可调检测器的检测性能。在计算机仿真中,N=64,K=96,虚警概率设置为P0=10-4。在图 1(a)中给出了SNR=20dB条件下检测概率随着cos2θ的变化关系,可以看到γ值取值的变化会导致检测性能与cos2θ关系也发生变化。当γ值较小时,可调检测器的性能与AMF接近,即对失配信号不敏感,检测概率较高。而当γ值较大时,可调检测器的性能与DN-AMF接近,即对失配的信号敏感,检测概率较低。因此从图中的分析来看,仿真结果和理论分析是一致的。图 1(b)给出了可调检测器检测性能与SNR和cos2θ的关系,此图也称之为Mesa图,是分析检测器对失配信号检测性能的理想工具。在图中分别给出了γ=1,0.5,0三种情况。可以看出,当γ=1对应了DN-AMF检测器,其检测性能受信号失配极为敏感,检测概率较高的部分主要集中在cos2θ=1附近。当γ=0对应了AMF检测器,其检测性能受信号失配不敏感,即使cos2θ趋近于0,只要SNR足够大,检测概率仍然较高。而当γ=0.5时,可调检测器的性能介于AMF与DN-AMF之间。因此调整参数γ可以实现检测器对失配信号敏感性的调整。
4.2空时导向矢量失配条件下的检测性能分析
接下来再分析该检测器对于空时2维导向矢量存在失配情况下的检测性能。考虑长度为Na个阵元构成的线性阵列,阵元之间的间距为半个波长,以阵列法向方向为角度零点,可以得到空间角度为φ的空间导向矢量va(φ),如果假定脉冲累积数目为Nc,目标归一化多普勒频率为fd,那么可以得到Nc维的时间导向矢量vt(fd)。考虑到雷达采用的空时联合处理,由此得到的Na×Nc维空时2维导向矢量v(fd,φ)是空间导向矢量和时间导向矢量的Kronecker乘积形式:
|
${{v}_{\rm{a}}}\left( \phi \right) = \left[ {\matrix{
1 \cr
{\exp \left( {j\cos \phi } \right)} \cr
\vdots \cr
{\exp \left( {j\left( {{N_{\rm{a}}} - 1} \right)\cos \phi } \right)} \cr
} } \right], \\
{{v}_{\rm{c}}}\left( {{f_{\rm{d}}}} \right) = \left[ {\matrix{
1 \cr
{\exp \left( {j2\pi {f_{\rm{d}}}} \right)} \cr
\vdots \cr
{\exp \left( {j\left( {{N_{\rm{c}}} - 1} \right)2\pi {f_{\rm{d}}}} \right)} \cr
} } \right], \\
{v}\left( {{f_{\rm{d}}}, \phi } \right) = {{v}_{\rm{c}}}\left( {{f_d}} \right) \otimes {{v}_{\rm{a}}}\left( \phi \right)$
|
(19)
|
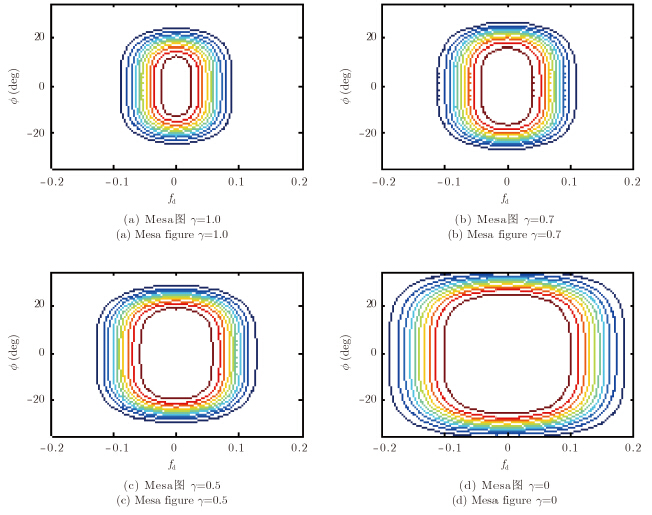
因此对于空时2维导向矢量失配问题,包含了归一化多普勒频率的失配和空间角度的失配。图 2给出了可调检测器在不同参数设置情况下,对导向矢量失配的检测性能。其中名义导向矢量的归一化多普勒频率为0,空间角度方向为法向,目标SNR=20dB,Na=Nc=8,考虑γ=1,0.7,0.5,0四种情况,得到的检测概率是归一化多普率频率fd和空间角度φ的函数。可以看出对于γ=1的情况,检测概率较高集中在(fd,φ)平面中心处,这说明检测器对导向矢量失配较为敏感。而随着γ逐渐减小,可以看出,检测概率较高的部分逐渐向四周扩散,这时检测性能对导向矢量失配敏感性降低。
4.3 可调检测器参数的选择
可调检测器的检测性能与参数γ的选择密切相关,因此有必要讨论针对特殊场景下的参数γ的选择问题。由图 1(b)可见,参数γ的选择目的就是尽可能保证少许失配的有用信号的检测能力,还要尽可能抑制严重失配的干扰信号。干扰信号与有用信号之间的差异是由失配程度cos2θ决定的,检测能力还受到SNR或干扰噪声比(Interference Noise Ratio,INR)的影响,参数γ的选择应该满足有用信号与干扰信号的检测概率之差δPd最大:
|
${\gamma ^ * } = {\max _\gamma }\delta {P_{\rm{d}}}\left( {{\rm{SNR}},{\rm{INR}},{{\cos }^2}{\theta _s},{{\cos }^2}{\theta _i};\gamma } \right)$
|
(20)
|
其中
|
$\delta {P_d}\left( {{\rm{SNR}},{\rm{INR}},{{\cos }^2}{\theta _s},{{\cos }^2}{\theta _i};\gamma } \right) \\
= {P_{\rm{d}}}\left( {{\rm{SNR}},{{\cos }^2}{\theta _s};\gamma } \right) - {P_{\rm{d}}}\left( {{\rm{INR}},{{\cos }^2}{\theta _i};\gamma } \right)$
|
(21)
|
其中有用信号失配最大角度为
θs,干扰信号失配最小角度为
θi。计算机仿真给出了
δPd与检测器的参数
γ的关系,仿真结果如
图 3所示,其中仿真参数
N=64,
K=96,SNR=INR=20dB,虚警概率设置为
P0=10
-4。考虑了4种情况,分别对应影响
δPd的4个参数。可以看出,这4种情况下,都存在一个最优的参数
γ值使得
δPd最大。
分别对比图中的4种情况,对于(θs=0.9,θi=0.1)与(θs=0.7,θi=0.1)两种情况,干扰信号的失配程度相同,而有用信号的失配程度有差异,那么对于失配程度较大的情况,参数γ值较小,从而使得检测器对有用信号失配敏感性减弱。对于(θs=0.9,θi=0.1)与(θs=0.9,θi=0.3)两种情况,有用信号的失配程度相同,而干扰信号失配程度有差异,那么对于干扰失配程度较大的情况,参数γ值较大,从而使得检测器对干扰的抑制能力增强。同样还可以对比(θs=0.9,θi=0.1)与(θs=0.7,θi=0.3)两种情况,有用信号与干扰信号失配程度同时增大,那么参数γ值基本不变,因为要保证信号的检测能力同时还需要考虑干扰的抑制能力。通过上述分析可以看出,对于可调检测器参数γ的选择,需要有关有用信号与干扰信号的相关信息。
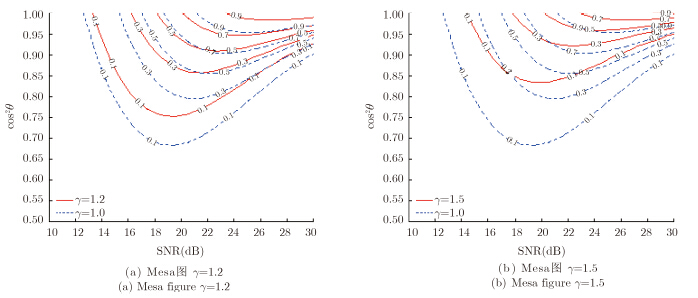
可调检测器参数的选择并不局限于0~1之间,为此分析γ>1的检测器性能。分析结果如图 4所示,仿真参数同前。可以看出,随着γ增大,检测器对失配信号的敏感性进一步增强。图 4(a)给出了γ=1.2的情况,相比于DN-AMF的检测性能(γ=1.0),其检测性能在Mesa图中进一步收缩到右上角,即表示对失配信号更加敏感。图 4(b)给出了γ=1.5的情况,可以看出,随着γ增大,检测器对失配信号的敏感性进一步增强。但需要指出的是,随着γ增大,检测器对匹配信号(cos2θ=1)的探测性能进一步减弱。因此检测器敏感性的提高是以对匹配信号检测性能损失为代价的。
5 结论
当考虑到有用信号与干扰并存,信号检测器必须同时具备信号的检测与干扰的抑制能力。然而由于有用信号可能存在的失配,检测器的设计上需要有一定的灵活性。为此本文给出了一种可调检测器,该检测器的参数γ控制了检测器对有用信号的检测能力,以及对干扰信号的抑制能力。检测器在结构上存在两个极端情况,当γ=0时,检测器性能与AMF相当,当γ=1时,检测器性能与DN-AMF相当。参数γ的选择与有用信号、干扰信号失配程度有关,如果能够获得这些先验信息,就可以唯一指定参数γ。需要指出的是,本文给出的检测器在γ>1时对失配信号具有更强的敏感性,但同时对匹配的有用信号的检测能力也会进一步减弱。


 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 3)
3) 2)
2) 1)
1) 3)
3) 1)
1) 1)
1) 1)
1) 1)
1) 3)
3) 1)
1) 1)
1) 1)
1) 1)
1) 2015, Vol. 4 Issue (4): 411–417
2015, Vol. 4 Issue (4): 411–417
