1 引言

广域监视运动目标检测在军事中和民用上都具有十分重要的作用。传统的广域监视采用Scan_ GMTI模式，该模式采用在方位向发射窄波束并通过方位波束的周期性扫描实现广域覆盖以及对运动目标的轨迹跟踪，该模式使用DBS成像方法，JSTARS系统和PAMIR系统^{[1, 2, 3]}是其典型代表。广域监视系统一般采用多通道多载频技术，能够很好地抑制鬼影目标^[4]。传统广域监视系统均采用机载系统，受到领空限制。

星载条件下DBS成像的方位分辨率较差，造成目标信杂比较低；方位向波束边缘的系统灵敏度(NESZ)比波束中心差6～12 dB，造成波束边缘目标的信噪比较差；这都不利于动目标检测。同时，波束扫描覆盖的成像带长度小于卫星波束在地面移动的距离，不利于实现对目标多次重访。为改善星载条件下动目标的信杂比和信噪比，借鉴TOPSAR设计思想，本文提出了一种基于星载TOPSAR的广域监视方法。

星载TOPSAR模式由意大利的Zan等人提出，并于2006年首次发表在文献^[5]上。该模式通过方位向周期性地调整天线波束指向，不但克服了ScanSAR模式的扇贝效应和方位模糊比在方位向严重不一致的问题，拥有大场景成像能力，并且星载SAR不受领空限制，因而十分适合广域监视。目前国内外对TOPSAR进行了系统的研究。文献_{^{[6, 7, 8]}}分析了星载TOPSAR模式的实现及系统性能；文献^[9]提出了一种高效处理TOPSAR数据的BAS(基带方位变标)算法；文献^[10]讨论了利用TOPSAR进行区域观测的方法；近年斜视TOPSAR成像算法日渐成熟^{[11, 12]}。在动目标检测方面，文献^[13]简单地分析了TOPSAR模式中微弱动目标检测能力；文献^[14]研究了正侧视TOPSAR-GMTI。目前为止，未见有对星载TOPSAR应用于动目标广域监视进行研究的文献资料。

本文第2节讨论了利用星载TOPSAR实现广域GMTI的方法；第3节根据建立的3通道TOPSAR-GMTI几何模型，给出了回波信号模型，并对回波信号模型进行了分析；第4节详细论述了斜视TOPSAR模式下，全孔径成像算法；第5节分析了TOPSAR-GMTI模式下动目标的检测与定位方法；第6节给出了斜视TOPSAR-GMTI的处理流程；第7节给出了仿真结果及分析，验证了本文方法的有效性；第8节对全文进行了总结。

2 广域GMTI模式实现方法

广域GMTI系统通过方位向波束扫描实现广域覆盖和对目标的多次重访，借鉴TOPSAR设计思想，本文提出一种基于TOPSAR的广域GMTI方法，该方法具体可分为两种工作模式：广域搜索和区域监视。

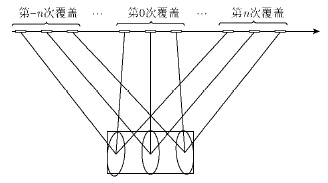
广域搜索采用TOPSAR的正常工作模式。区域监视利用方位向波束扫描，实现对特定区域的多次扫描覆盖，每次扫描成像都采用TOPSAR成像原理进行成像，图 1是其工作原理示意图。如图所示，每次方位波束扫描结束，天线波束并不是改变距离向波束指向，而是改变方位角再次对同一区域进行扫描成像。比如假设图中第-n次扫描时，波束的方位角为${30^ \circ }$，第$ - \left( {n - 1} \right)$次扫描时，波束的方位角改变为${28^ \circ }$，使得波束仍旧扫描覆盖同一区域，在每一次的扫描中，天线波束在方位向从后向前扫描，扫描角大小根据系统需求而定。该模式可以实现对重点区域进行持续监视，对区域中的动目标进行跟踪。

其中第0次覆盖为正侧视TOPSAR工作方式，其它次数的覆盖为斜视TOPSAR工作方式。本文将主要讨论斜视TOPSAR模式下的运动目标检测算法，该算法同样适用于正侧视TOPSAR。

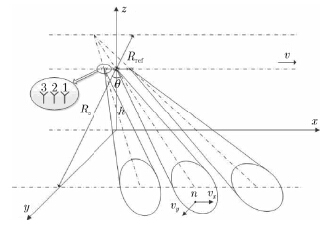
3 信号模型

斜视TOPSAR模式的几何模型如图 2所示。卫星运行高度为h，以速度v沿x轴飞行，R_s表示场景中心到航迹的最短斜距，R_ref表示天线波束虚拟旋转中心到航迹的最短斜距，天线波束的斜视角为θ,3通道天线沿航迹以间距D排列，采用全天线发射信号，3个天线同时接收的工作方式。3根天线均沿航迹方向从后向前进行扫描。运动目标n位于(x_n,y_n,0)处，速度为(v_x,v_y)。

因为R_s>>D，所以采用等效相位中心原理可得动目标在t 时刻与第i 个天线相位中心之间的距离为：

$\eqalign{ & {R_{i,n}} = \sqrt {{{\left( {{x_n} + {v_x}t - {d_i} - vt} \right)}^2} + {{\left( {{y_n} + {v_y}t} \right)}^2} + {h^2}} \cr & \qquad {\rm{ }} \approx {R_n} + {{x_n^2} \over {2{R_n}}} + {{d_i^2 - 2{x_n}{d_i}} \over {2{R_n}}} \cr & \qquad \quad {\rm{ }} + {{\left( {{d_i} - {x_n}} \right)\left( {v - {v_x}} \right) + {v_y}{y_n}} \over {{R_n}}}t \cr & \qquad \quad \, {\rm{ + }}{{{{\left( {v - {v_x}} \right)}^2} + v_y^2} \over {2{R_n}}}{t^2} \cr} $

(1)

其中t 表示慢时间，${R_n} = \sqrt {y_n^2 + {h^2}} ,{d_1} = D/2,{d_2} = 0,{d_3} = - D/2$分别表示各天线等效相位中心与发射天线等效相位中心之间的间隔。令

$\begin{gathered} {R_i} = {R_n} + \frac{{x_n^2}}{{2{R_n}}} + \frac{{d_i^2 - 2{x_n}{d_i}}}{{2{R_n}}} \hfill \\ {A_{i{\text{ }}}} = ({d_i} - {x_i})(v - {v_x}) + {v_y}{y_n},B = {(v - {v_x})^2} + v_y^2 \hfill \\ \end{gathered}$

则${R_{i,n}}$可整理为：

${R_{i,n}} = {R_i} + {{{A_i}} \over {{R_n}}}t + {B \over {2{R_n}}}{t^2}$

(2)

假设发射信号为调频率为${k_{\rm{r}}}$的线性调频信号，目标反射信号经去载频后可得各通道的回波信号为：

$\begin{gathered} {s_i}\left( {\tau ,t} \right) = {\sigma _n}{w_{\text{r}}}\left( {\tau - \frac{{{R_{i,n}} + {R_{2,n}}}}{{\text{c}}}} \right){w_a}\left( {\frac{{t - {t_0}}}{{{T_{\text{a}}}}}} \right) \hfill \\ {\text{ }} \cdot \exp \left( { - {\text{j}}2\pi \frac{{{R_{i,n}} + {R_{2,n}}}}{\lambda }} \right) \hfill \\ {\text{ }}\quad \quad \quad \; \cdot \exp \left( {{\text{j}}\pi {k_r}{{\left( {\tau - \frac{{{R_{i,n}} + {R_{2,n}}}}{c}} \right)}^2}} \right) \hfill \\ \end{gathered} $

(3)

其中${\sigma _n}$表示目标的回波振幅，$\tau $表示快时间，$c$表示光速，$\lambda $表示载波波长，${w_r}( \cdot )$和${w_a}( \cdot )$分别表示距离向和方位向的窗函数，${t_0}$表示目标的波束中心穿越时刻，${T_a}$表示合成孔径时间。 4 斜视TOPSAR成像算法

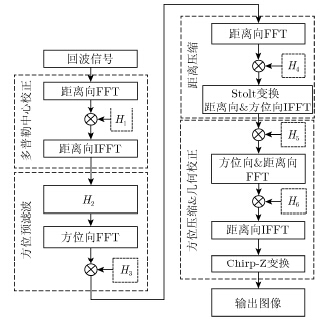
本文采用斜视TOPSAR成像算法对回波信号进行聚焦成像，其流程如图 3所示，主要包括4部分：多普勒中心频率校正、方位预滤波、距离向压缩以及方位压缩和几何校正。下面详细分析各步骤。

4.1 校正多普勒中心频率

将回波信号变换到$\left( {{f_{\rm{r}}},t} \right)$域，其表达式为：

$\eqalign{ & {s_i}\left( {{f_{\rm{r}}},t} \right) = {w_{\rm{r}}}\left( {{{{f_{\rm{r}}}} \over {{B_{\rm{r}}}}}} \right){w_{\rm{a}}}\left( {{{t - {t_0}} \over {{T_{\rm{a}}}}}} \right)\exp \left( { - {\rm{j}}\pi {{f_{\rm{r}}^2} \over {{k_{\rm{r}}}}}} \right) \cr & \qquad \qquad \, {\rm{ }} \cdot {\rm{exp}}\left( { - {\rm{j}}{{2\pi \left( {{f_{\rm{r}}} + {f_{\rm{c}}}} \right)} \over {\rm{c}}}\left( {{R_{i,n}} + {R_{2,n}}} \right)} \right) \cr} $

(4)

式中省略了部分系数，其中${f_{\rm{r}}}$表示距离频率，${f_{\rm{c}}}$表示载波频率。

斜视角使得回波具有非零的多普勒中心频率和2维频谱的扭曲等问题，前者将导致多普勒谱平移和多普勒模糊，最终使成像结果出现鬼影，后者来源于多普勒中心频率随距离频率变化，将致使目标散焦。本文在距离频域方位时域采用非线性平移法来解决这两个问题，方法是将回波信号与式(5)相乘，然后把信号变回时域，得到${s_i}\left( {\tau ,t} \right)$。

${H_1} = \exp \left( { - {\rm{j}}{{4\pi \left( {{f_r} + {f_c}} \right)} \over c}v\sin \theta t} \right)$

(5)

4.2 方位向预滤波

TOPSAR采用方位扫描，虽然等效压缩了单点目标的多普勒带宽，但是整个场景的方位带宽却因此大大扩展，甚至远大于系统PRF，导致方位频谱混叠。本文使用方位向预滤波的方法来实现方位频谱去混叠^[15]，将信号与函数${H_2} = \exp \left( { - {\rm{j}}\pi {{2{v^2}} \over {\lambda {R_{{\rm{ref}}}}}}{t^2}} \right)$在时域进行卷积运算，实现信号的预压缩，卷积运算可以利用快速傅里叶变换(FFT)实现，具体包括两次复乘和一次FFT。虽然信号经过了FFT变换，但由于预滤波的实质是时域卷积运算，因此预滤波后的信号仍然是时域信号，设新的方位时间为$t'$。

对预滤波后的信号进行2维傅里叶变换，得到信号的2维频谱为：

$\begin{align} & {{s}_{i}}\left( {{f}_{\text{r}}},f_{\text{a}}^{'} \right) \!\!\! = \!\!\! { {w}_{\text{r}} \! }\left( \!\! \frac{{{f}_{\text{r}}}}{{{B}_{\text{r}}}} \!\! \right) \!\! {{w}_{a}} \!\! \left( \!\! \frac{\!-\! \frac{\lambda }{2}\left( 1 \!+ \! \frac{{{v}^{2}}{{R}_{n}}}{B{{R}_{\text{ref}}}} \right)f_{\text{a}}^{'} \!\!\! - \!\!\! \frac{{{v}^{2}}{{A}_{i}}}{B{{R}_{\text{ref}}}} \!\!- \!\! \frac{{{A}_{i}}}{{{R}_{n}}}}{\frac{B}{{{R}_{n}}} \! +\! \frac{{{v}^{2}}}{{{R}_{\text{ref}}}}} \!\! \right) \exp \left( \!\!- \!\! \text{j}\pi \frac{f_{\text{r}}^{2}}{{{k}_{\text{r}}}} \!\! \right) \\ & \qquad \qquad \quad \exp \left( \!\! \text{j}2\pi {{f}_{\text{r}}}\left( \frac{A_{i}^{2}}{cB{{R}_{n}}} \!\! + \!\! \frac{{{v}^{2}}{{\sin }^{2}}\theta }{cB}{{R}_{n}} \!\! - \!\! \frac{2{{R}_{i}}}{c} \right) \!\! \right) \\ & \qquad \qquad \text{ }\cdot \exp \left( \text{j}4\pi \frac{v\sin \theta {{A}_{i}}}{cB}{{f}_{\text{r}}} \right)\exp \left( \text{j}\pi \frac{{{f}_{\text{c}}}}{{{f}_{\text{r}}}+{{f}_{\text{c}}}}\frac{\lambda {{R}_{n}}}{2B}f{{_{\text{a}}^{'}}^{2}} \right)\text{exp}\left( \text{j}\pi \frac{\lambda {{R}_{\text{ref}}}}{2{{v}^{2}}}f{{_{\text{a}}^{'}}^{2}} \right) \\ & \qquad \qquad \quad \exp \left( \text{j}2\pi \frac{{{R}_{n}}v\sin \theta }{B}f_{\text{a}}^{'} \right)\exp \left( \text{j}2\pi \frac{{{A}_{i}}}{B}f_{\text{a}}^{'} \right) \\ & \qquad \qquad \text{ }\cdot \exp \left( \text{j}2\pi \left( \frac{A_{i}^{2}}{cB{{R}_{n}}}+\frac{{{v}^{2}}{{\sin }^{2}}\theta }{cB}{{R}_{n}}+\frac{2v\sin \theta {{A}_{i}}}{cB}-\frac{2{{R}_{i}}}{c} \right) \right) \\ \end{align}$

(6)

式中$f_{\text{a}}^{'}$表示新的方位频率，与$t'$相对应。式(6)的相位项中，第1项代表距离压缩部分；第2项代表RCMC部分；第3项表示方位向和距离向耦合部分，此项主要是由于斜视TOPSAR时，同一距离门不同方位位置的目标斜距变化很大导致，因此应在成像后对其进行校正；第4项表示带有耦合的方位调制项；第5项是方位预滤波引入的相位，应在距离向处理前乘以${H_3} = \exp \left( { - j\pi {{\lambda {R_{ref}}} \over {2{v^2}}}{{f'}_a}} \right)$将其补偿掉；第6项同第3项一样，表示距离向和方位向的耦合，因为最终成像结果在距离多普勒域(RD域)，因此应在时域对该项进行校正；第7项代表由于目标运动和通道间距引起的多普勒中心偏移。 4.3 距离压缩和RCMC

不失一般性，对静止目标进行分析，回波信号经过方位向预滤波处理后的2维频谱可表示为：

$\begin{align} & \hat{s}\left( {{f}_{\text{r}}},f_{\text{a}}^{'} \right) \!\!\! = \!\!\! {{w}_{\text{r}}}\left( {{f}_{\text{r}}} \right){{w}_{\text{a}}}\left( f_{\text{a}}^{'} \right)\exp \left( -\text{j}\pi \frac{f_{\text{r}}^{2}}{{{k}_{\text{r}}}} \right)\exp \left( -\text{j}\frac{4\pi \left( {{f}_{\text{r}}}+{{f}_{\text{c}}} \right)}{\text{c}}{{R}_{n}}{{\sin }^{2}}\theta \right) \\ & \qquad \qquad \; \,\exp \left( -\text{j}\frac{4\pi }{\text{c}}\sqrt{{{\left( {{f}_{\text{r}}}+{{f}_{\text{c}}} \right)}^{2}}-{{\left( \sin \theta \left( {{f}_{\text{r}}}+{{f}_{\text{c}}} \right)+\frac{\text{c}f_{\text{a}}^{'}}{2v} \right)}^{2}}} \right) \\ & \qquad \qquad \text{ }\cdot \text{exp}\left( -\text{j}\frac{4\pi \left( {{f}_{\text{r}}}+{{f}_{\text{c}}} \right)}{\text{c}}{{x}_{n}}\sin \theta \right)\exp \left( -\text{j}2\pi \frac{{{R}_{n}}\sin \theta }{v}f_{\text{a}}^{'} \right)\exp \left( -\text{j}2\pi \frac{{{x}_{n}}}{v}f_{\text{a}}^{'} \right) \\ \end{align}$

(7)

由式(7)可得距离压缩可以通过匹配滤波实现，RCMC可以通过Stolt变换实现，其具体方法是，首先将经过相位补偿后的2维频域信号与式(8)相乘

$\begin{align} & {{H}_{4}}=\exp \left( -\text{j}\pi \frac{f_{\text{r}}^{2}}{{{k}_{\text{r}}}} \right)\exp \left( -\text{j}\frac{4\pi {{R}_{n}}\cos \theta }{c}\sqrt{{{\left( {{f}_{\text{r}}}+{{f}_{\text{c}}} \right)}^{2}}-{{\left( \sin \theta \left( {{f}_{\text{r}}}+{{f}_{\text{c}}} \right)+\frac{\text{c}f_{\text{a}}^{'}}{2v} \right)}^{2}}} \right) \\ & \qquad \text{ }\cdot \exp \left( \text{j}\frac{4\pi {{R}_{n}}\cos \theta }{c}\sqrt{{{f}_{c}}^{2}-{{\left( \sin \theta {{f}_{c}}+\frac{\text{c}f_{\text{a}}^{'}}{2v} \right)}^{2}}} \right) \\ \end{align}$

(8)

接着，对信号进行Stolt变换，变换核为：

${{f}_{\text{r}}}=\sqrt{{{\left( {{f}_{\text{r}}}+{{f}_{\text{c}}} \right)}^{2}}-{{\left( \sin \theta \left( {{f}_{\text{r}}}+{{f}_{\text{c}}} \right)+\frac{\text{c}f_{\text{a}}^{'}}{2v} \right)}^{2}}}-\sqrt{{{f}_{\text{c}}}^{2}-{{\left( \sin \theta {{f}_{\text{c}}}+\frac{\text{c}f_{\text{a}}^{'}}{2v} \right)}^{2}}}$

(9)

4.4 方位压缩和几何校正

经过距离压缩和RCMC后可得到信号在RD域的表达式为：

${{s}_{i}} \! \left( \! \tau ,f_{\text{a}}^{'} \! \right)\text{=}{{w}_{\text{a}}}\left( \! f_{\text{a}}^{'} \! \right)\!\! \exp \!\! \left( \text{j}\pi \frac{\lambda {{R}_{n}}}{2B}f{{_{\text{a}}^{'}}^{2}} \right)\!\! \exp \!\! \left(\! \text{j}2\pi \frac{{{R}_{\text{r}}}v\sin \theta }{B}f_{\text{a}}^{'} \! \right)\!\! \text{exp} \!\! \left(\! -\! \text{j}2\pi \frac{{{x}_{n}}\left( v-{{v}_{x}} \right)-{{v}_{y}}{{y}_{n}}}{B}f_{\text{a}}^{'} \! \right)\!\! \exp \!\! \left( \text{j}2\pi \frac{{{d}_{i}}}{v}f_{\text{a}}^{'} \right)\text{ }$

(10)

其中未考虑慢时间项，${R_{\rm{r}}}$表示目标与场景中心在距离向的距离。式(10)表明通道间隔将导致各通道的时域图像有相对移位，因此应该将其补偿掉，即将信号与式(11)相乘

${H_{{\rm{i}},a}} = \exp \left( { - j2\pi {{{d_i}} \over v}{{f'}_a}} \right)$

(11)

把补偿通道位移后的信号变换到时域，信号表达式为：

$\eqalign{ & {s_i}\left( {\tau ,t'} \right){\rm{ = }}\exp \left( { - {\rm{j}}\pi {{\lambda {R_n}} \over {2B}}t{'^2}} \right)\exp \left( { - {\rm{j}}2\pi {{2B} \over {\lambda {R_n}}}{{{R_{\rm{r}}}v\sin \theta } \over B}t'} \right) \cr & {\rm{ }} \cdot {\rm{exp}}\left( { - {\rm{j}}2\pi {{2B} \over {\lambda {R_n}}}{{{x_n}\left( {v - {v_x}} \right) - {v_y}{y_n}} \over B}t'} \right){\rm{ }} \cr} $

(12)

其中第1项是调频项；第2项是前面提到的需要补偿掉的耦合项；第3项由运动目标引起，使得成像后目标在方位向发生移位。通过与式(13)相乘对时域信号进行去调频和相位补偿

${H_5} = \exp \left( {{\rm{j}}\pi {{\lambda {R_{\rm{c}}}} \over {2B}}t{'^2}} \right)\exp \left( {{\rm{j}}2\pi {{2B} \over {\lambda {R_{\rm{c}}}}}{{{R_{\rm{r}}}v\sin \theta } \over B}t'} \right)$

(13)

其中${R_{\rm{c}}}$为场景中心沿斜视角方向的最短斜距。经过方位去调频处理后，目标在RD域的表达式为式(14)，其中第1项表示目标距离向位置，它表明目标距离向位置和方位向位置存在耦合，本文通过在距离频域乘以${H_6} = {\rm{exp}}\left( { - {\rm{j}}{{4\pi {x_n}\sin \theta } \over c}{f_{\rm{r}}}} \right)$；第2项是目标在方位向的位置，可以看出其方位位置存在几何形变，通过Chirp-Z变换可以校正该项，同时方位位置与目标的运动和实际位置有关，因此通过该项可获得目标的实际位置；第3项表明目标的径向速度会引起多普勒平移；第4项表示目标的径向速度和通道间隔将导致各通道相位不一致，因此可通过各通道相位差异得到目标的径向速度；第5项是目标径向速度引入的相位项。

$\begin{align} & {{s}_{i}}\left( \tau ,f_{\text{a}}^{'} \right)={{\widehat{\sigma }}_{n}}\text{sinc}\left( \Delta {{f}_{\text{r}}}\left( \tau -\frac{2{{R}_{n}}}{\text{c}}+\frac{2v\sin \theta {{A}_{i}}}{\text{c}B} \right) \right) \\ & \qquad \qquad \qquad \text{sinc}\left( \pi \left( 1\text{+}\frac{B{{R}_{\text{ref}}}}{{{v}^{2}}{{R}_{n}}} \right)\left( f_{\text{a}}^{'}-\frac{2{{x}_{n}}\left( v-{{v}_{x}} \right)-2{{y}_{n}}{{v}_{y}}}{\lambda \left( {{R}_{n}}+\frac{B{{R}_{\text{ref}}}}{{{v}^{2}}} \right)} \right) \right) \\ & \qquad \qquad \text{ }\cdot \text{exp}\left( \text{j}2\pi \frac{{{R}_{n}}-{{R}_{\text{ref}}}}{{{R}_{n}}}\frac{{{y}_{n}}{{v}_{y}}}{{{v}^{2}}}f_{\text{a}}^{'} \right)\exp \left( \text{j}2\pi \frac{2{{y}_{n}}{{v}_{y}}}{\lambda v}\frac{1}{{{R}_{n}}+{{R}_{\text{ref}}}}{{d}_{i}} \right) \\ & \qquad \qquad \qquad \text{exp}\left( -\text{j}2\pi \left( \frac{2{{R}_{n}}}{\lambda }+\frac{2{{x}_{n}}{{y}_{n}}{{v}_{y}}}{\lambda v{{R}_{n}}} \right) \right) \\ \end{align}$

(14)

5 运动目标检测与定位 5.1 杂波对消与动目标检测

本文采用DPCA方法进行杂波对消，得到各通道信号RD域图像后，将通道1图像减去通道2图像可得S₂₁，通道3图像减去通道2图像可得S₃₂

$\begin{align} & {{S}_{21}}=\text{j}2{{s}_{2}}\left( \tau ,f_{\text{a}}^{'} \right)\sin \left( -\frac{2\pi {{y}_{n}}{{v}_{y}}}{\lambda v}\frac{1}{{{R}_{n}}+{{R}_{\text{ref}}}}\left( {{d}_{2}}-{{d}_{1}} \right) \right) \\ & \qquad \, \, \text{ }\cdot \text{exp}\left( -\text{j}\frac{2\pi {{y}_{n}}{{v}_{y}}}{\lambda v}\frac{1}{{{R}_{n}}+{{R}_{\text{ref}}}}\left( {{d}_{2}}-{{d}_{1}} \right) \right) \\ \end{align}$

(15)

$\begin{align} & {{S}_{32}}=\text{j}2{{s}_{2}}\left( \tau ,f_{\text{a}}^{'} \right)\sin \left( \frac{2\pi {{y}_{n}}{{v}_{y}}}{\lambda v}\frac{1}{{{R}_{n}}+{{R}_{\text{ref}}}}\left( {{d}_{3}}-{{d}_{2}} \right) \right) \\ & \qquad \, \, \text{ }\cdot \text{exp}\left( \text{j}\frac{2\pi {{y}_{n}}{{v}_{y}}}{\lambda v}\frac{1}{{{R}_{n}}+{{R}_{\text{ref}}}}\left( {{d}_{3}}-{{d}_{2}} \right) \right) \\ \end{align}$

(16)

由式(15)和式(16)可知，对于静止目标${v_y} = 0$，则${S_{21}} = {S_{32}} = 0$，对于动目标${v_y} \ne 0$，则$\left| {{S_{21}}} \right|,\left| {{S_{32}}} \right| > 0$，信号将被保留下来，由此可知DPCA方法可有效用于TOPSAR进行杂波对消。对${S_{21}}$进行CFAR检测^{[16, 17]}，并对结果进行点迹凝聚，检测出动目标。

5.2 动目标参数估计

根据式(15)和式(16)可知，动目标的径向地速信息隐藏在相位中，通过对S₂₁和S₃₂共轭相乘，然后提取出相位信息，可以计算得到目标的径向地速为：

${v_y} = - {{\lambda v} \over {2\pi D}}{{{R_n} + {R_{{\rm{ref}}}}} \over {{y_n}}}\varphi $

(17)

其中$\varphi = {\rm{angle}}\left( {{S_{32}} \cdot {\rm{conj}}\left( {{S_{21}}} \right)} \right)$表示${S_{21}}$和${S_{32}}$的干涉相位。结合实际道路信息，我们可以得到目标沿航迹的速度${v_x}$。

由于$\varphi $的取值以2$\pi $为周期，当${v_y} > {{\lambda v\left( {{R_n} + {R_{{\rm{ref}}}}} \right)} \over {2{y_n}D}}$或${v_y} < - {{\lambda v\left( {{R_n} + {R_{ref}}} \right)} \over {2{y_n}D}}$时干涉相位有缠绕现象，即$\varphi = {\varphi _0} \pm 2n\pi ,n = 0,1,2, \cdots $。由式(17)可知，模糊问题涉及通道数目、天线全孔径尺度、载频频率、雷达平台运行参数等方面的设计。在解模糊方面目前有基于压缩感知的相位解模糊方法^[18]，以及PAMIR采用的多载频技术^[1]。本文建议采用多载频技术，其不仅能实现解相位模糊，并且还能优化DPCA体制具有的盲速问题。

由式(14)可得目标在图像中的真实位置为：

${\hat f_{{\rm{a}}t}} = {f_{{\rm{a}}t}} + {{2{y_n}{v_y}} \over {\lambda \left( {{R_n} + {{B{R_{{\rm{ref}}}}} \over {{v^2}}}} \right)}}$

(18)

其中${f_{{\rm{a}}t}}$为SAR图像中目标所在的方位位置，据此可以将SAR图像中的动目标校正到正确的位置。进一步可以得到动目标的真实地理方位位置为：

${\hat x_n} = {{\lambda \left( {{R_n} + {{B{R_{{\rm{ref}}}}} \over {{v^2}}}} \right){{\hat f}_{{\rm{a}}t}}} \over {2\left( {v - {v_x}} \right)}} \approx {{\lambda \left( {{R_n} + {R_{{\rm{ref}}}}} \right){{\hat f}_{{\rm{a}}t}}} \over {2v}}$

(19)

6 斜视TOPSAR-GMTI算法流程

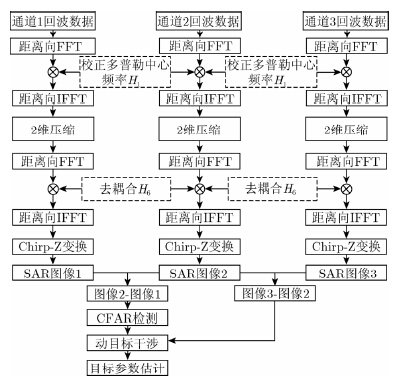
综合前文，本节给出3通道斜视TOPSAR- GMTI算法的处理流程，如图 4所示。

第1步 在距离频域乘以H₁完成多普勒中心频率校正；

第2步 进行方位预滤波处理，具体方法是将信号与参考相位H₂相乘，然后进行方位傅里叶变换，再补偿一个相位${\widehat H_2} = \exp \left( { - {\rm{j}}\pi {{2{v^2}} \over {\lambda {R_{{\rm{ref}}}}}}{{t'}^2}} \right)$，接着将信号进行方位傅里叶变换到RD域后与补偿相位H₃相乘；

第3步 在2维频域乘以H₄完成距离向压缩，利用Stolt变换完成RCMC；

第4步 在时域乘以H₅完成方位去调频后将信号变换到RD域得到2维压缩后的图像；

第5步 在距离频域乘以H₆去耦合后变回到RD域，然后进行Chirp-Z变换完成几何校正，得到最终成像图。由H₆的表达式可知去耦合与方位位置有关，但此时动目标的方位位置偏离了原始位置，这导致在校正后的图像中，动目标的距离向位置会偏离其原始位置，其大小为$\Delta x\sin \theta $，在动目标重定位时应该将其修正；

第6步 利用DPCA方法，得到两两相消的图像S₂₁和S₃₂，采用CFAR检测在S₂₁中检测动目标位置；

第7步 利用干涉相位与动目标速度关系，求解出动目标的参数，并将动目标的正确位置标注在图像中。

图 4中的2维压缩部分包含第2步到第4步3个步骤。

7 仿真结果及分析

为验证本文提出的广域GMTI方法，本节给出了仿真结果，并对其进行分析。仿真参数如表 1所示。

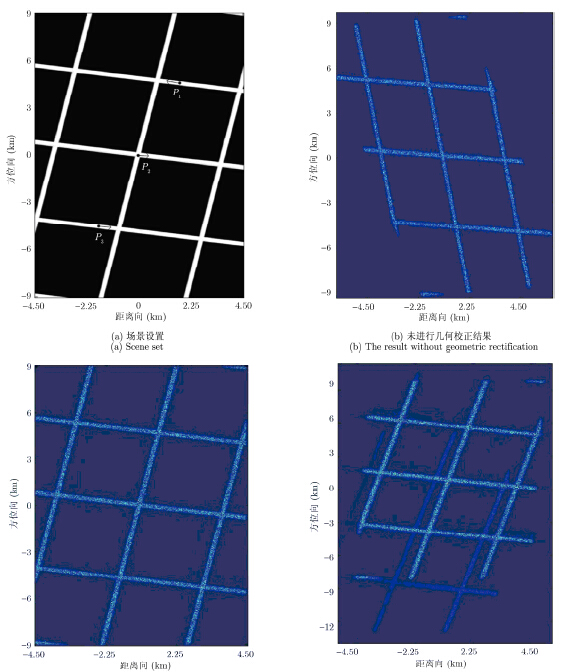
仿真场景设置为模拟的城市街道，大小为(18 km×9 km)，场景中心零多普勒斜距为577 km，横纵街道互相垂直分布，纵向街道(即沿方位向的街道)与雷达飞行方向夹角为$10^\circ $，在场景中有3个运动点目标(P₁,P₂,P₃)分别沿横向道路移动，径向地速分别为-5 m/s,18 m/s,5 m/s，方位向地速分别为0.9 m/s,-3.2 m/s,-0.9 m/s，如图 5(a)所示，仿真时P₁,P₂信杂比设置为0 dB,P₃信杂比设置为-5 dB。

图 5(b)是经过了2维压缩聚焦但未进行几何校正的成像结果，从图中可以看出由于斜视角的存在使得成像结果有很大的几何形变，需要进行几何校正，与前文分析一致；图 5(c)是采用本文成像算法得到的成像结果，由图可知经过两次几何校正后，几何形变量得到很好地校正，并且由图可知动目标淹没在背景杂波中；图 5(d)是采用文献^[14]成像算法得到的成像结果，对比看出，文献^[14]得到的结果存在明显的鬼影目标，由此可知该方法不适用于斜视TOPSAR成像。

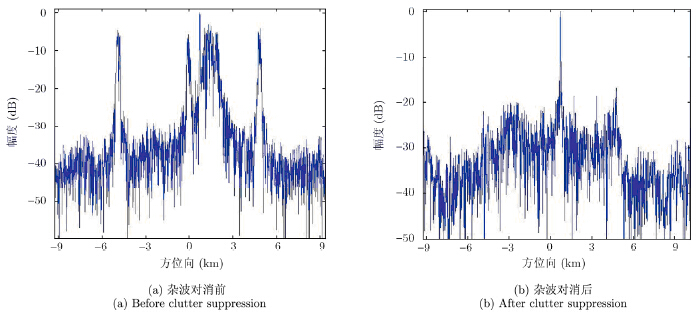
图 6是杂波对消前后的对比图，图 6(a)是杂波抑制之前的幅度图，图 6(b)是杂波抑制之后的幅度图。由图可知DPCA能很好地抑制杂波，并同时保留动目标。

表 2是对检测出的动目标进行参数估计的结果，由表 2可知本文算法可以较准确地估计出目标的真实参数。

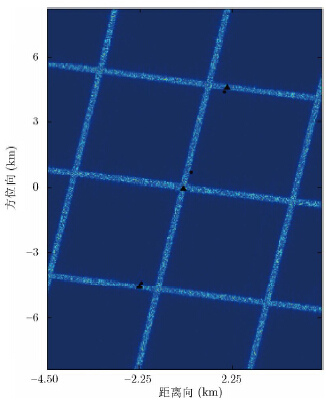
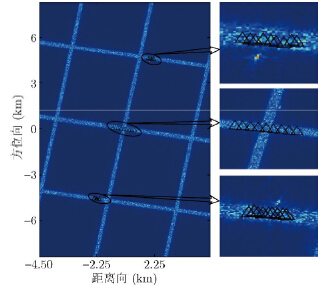
图 7是经过CFAR检测后的结果图，可以看出经过杂波抑制后，运动目标能够很好地被检测出来。图 8是对运动目标进行重定位的结果图，●表示定位前的位置，▲表示定位后的位置，可以看出动目标都被定位到了正确的位置，从定位的结果可以清晰地观察到第6节第5步分析得到的动目标的距离向偏移。图 9是区域监视的结果图，监视期间，斜视角变化范围为$ - 21^\circ \sim 21^\circ $，时长为64 s，包含120次扫描，每隔8 s(20次扫描)选取一次结果，由图可知本文提出的广域GMTI模式能够对动目标进行跟踪，验证了方法的有效性。

实际上，真实数据与仿真数据之间存在一定的差异，这些差异会导致真实数据的处理结果并不理想，因此在处理真实数据时需要对数据进行额外处理，主要差异包含以下几部分：

(1) 通道失配。通道失配误差会影响杂波对消效果，导致动目标的检测和参数估计性能变差，可以通过在成像处理前进行通道均衡，减小通道失配带来的误差。

(2) 雷达平台的运动误差。雷达平台并不是进行理想的匀速直线运动，其运动存在随机扰动项，这将导致成像结果变差，进而影响后期的动目标检测和参数估计，机载平台上，影响更明显，可以通过运动补偿来减小误差影响。

(3) 强背景杂波。在城市中，存在一些强散射杂波，这些杂波导致杂波对消效果变差，使动目标检测变得更加困难，甚至失效。此时，可以通过幅相联合检测来提高检测性能，即同时使用DPCA和ATI(沿迹干涉)来加强对杂波的抑制和对动目标的检测；也可以采用效果更好的STAP(空时自适应)杂波抑制方法来进行杂波抑制和动目标检测。

8 结束语

相比ScanSAR,TOPSAR既拥有宽测绘带的优势，又克服了ScanSAR的扇贝效应和方位模糊比问题。本文提出了一种基于TOPSAR的星载广域GMTI方法，该方法有两种运行模式：广域搜索和区域监视。广域搜索拥有宽测绘带的能力，能同时监视大范围区域动目标情况；区域监视拥有区域重访功能，能对重点目标进行轨迹跟踪。文章对区域监视模式进行了着重介绍，给出了回波数学模型，分析了斜视TOPSAR情况下的成像算法，与正侧视相比，主要增加了多普勒中心校正模块，仿真表明不校正多普勒中心会导致图像出现鬼影。仿真数据的处理结果验证了方法的有效性。本文也对真实数据和仿真数据之间的差异进行了讨论分析。本文方法存在数据量过大，不利于数据下传的问题，接下来的研究将围绕数据压缩进行。