空时自适应处理(Space-Time Adaptive Processing,STAP)雷达联合空间与时间2维信息,能够检测淹没于杂波背景中的微弱目标信号,在机载预警雷达中具有重要的应用价值[1, 2]。在正侧视机载雷达中,杂波的空域频率与多普勒频率之间是线性耦合的,且该耦合关系是不随距离而变化的,因而不同距离获得的训练样本可近似认为满足独立同分布特性。而在前视机载雷达中,杂波分布具有严重的距离依赖性,训练样本的独立同分布性不再满足,导致STAP方法性能的严重下降[3]。更严重的是在高脉冲重复频率雷达还存在距离模糊杂波带来的复杂问题。当存在距离模糊时,运动目标不仅要与无模糊距离杂波竞争,而且要与模糊距离杂波竞争,低信噪比信号将完全淹没在杂波中。无模糊距离区与模糊距离区的杂波在时域上混在一起,而其相应的杂波特性却有很大区别,因此传统STAP方法在这种情况下性能严重下降。
如上所述,前视阵机载雷达STAP方法面临的两个关键问题是杂波的距离依赖问题与距离模糊问题。国内外学者在距离依赖补偿方面开展了大量的研究工作,包括:导数更新法[4]、多普勒弯曲法[5]、角度多普勒补偿法[6]、自适应角度多普勒补偿法[7, 8]、高阶多普勒弯曲法[9]、配准补偿法[10, 11]、联合空时插值法[12]等。然而,现有方法均在无距离模糊的条件下展开讨论的。当距离模糊与距离依赖同时存在时,现有方法性能恶化甚至失效。3维STAP考虑利用俯仰自由度解决距离模糊杂波抑制问题,但是该方法运算量复杂,且需要大量的训练样本[13, 14]。因而3维STAP技术难以在实际中得到应用。文献[15]提出了一种利用频率分集阵列(Frequency Diverse Array,FDA)雷达距离角度依赖的方向图改善距离模糊的STAP算法。与传统相控阵不同,FDA利用阵元间微小的频率步进量,能够产生角度、距离、时间相关的天线方向图,利用其发射方向图的距离维零点可以有效实现距离模糊杂波抑制。文献[16]基于FDA提出了正侧视阵列距离模糊杂波情况下目标检测方法,充分利用了FDA提供了可控自由度,有效地解决了距离模糊杂波抑制问题。另外,文献[17, 18]还提出了一种将多输入多输出技术与FDA技术相结合的双基频率分集系统,能够形成不依赖角度的发射方向图。文献[19]指出了FDA提供的多维可控自由度,具有实现多功能多任务的潜力。
本文建立一种基于频率分集体制的STAP雷达信号模型,提出了利用FDA在距离维的可控自由度实现距离模糊杂波抑制的方法。频率分集阵列的发射导向矢量是距离的函数,因此FDA利用其距离维可控自由度可实现无模糊距离区和模糊距离区杂波的区分。与文献[16]不同,本文通过构造空间频率域的子空间投影矩阵,可有效地实现距离模糊杂波的分离,并将子空间投影方法与传统杂波谱补偿方法相结合,同时解决了距离依赖和距离模糊杂波抑制问题。仿真实验验证了本文方法的有效性。
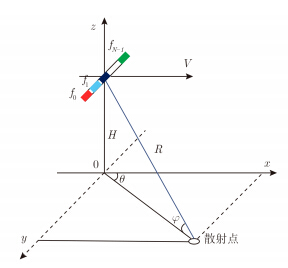
2 FDA-STAP雷达信号模型前视FDA-STAP雷达的几何构型如图 1所示。雷达相干脉冲数为K,脉冲重复频率为fr。平台速度为V,飞行方向与阵列法线方向一致。假定阵列为列合成后的1维等距线阵,阵列由N个等效阵元组成,阵元间距为d。第n个阵元的发射载频为:
| ${f\!_n} = {f\!_0} + \left( {n - 1} \right)\Delta f,\ n = 1,2,\cdots,N$ | (1) |
|
图 1 前视FDA-STAP雷达的几何模型 Fig. 1 Geometry of forward-looking FDA-STAP radar |
其中,f0为参考载频,Δf为频率步进量。
假设所有阵元发射正交波形,且回波信号在接收机中通过匹配滤波进行有效的分离,并对分离后的回波信号中包含相同发射载频的回波进行波束形成。这一步骤等效于阵列雷达由单阵元发射,由全孔径天线接收。对任意散射点,其到第n个阵元的斜距可以表示为R–(n–1)dsinθcosφ,这里R代表参考斜距,θ为方位角、φ为俯仰角。因此,由全阵列孔径接收的第n个阵元发射的信号相位可表示为:
| ${\psi _n} = \frac{{2\pi f{_n}}}{{\rm{c}}}\left[{2R - \left( {n - 1} \right)d\sin \theta \cos \varphi } \right]$ | (2) |
其中,c代表光速。第1个阵元接收的信号相位为${\psi _1} = \frac{{4\pi f{_0}R}}{{\rm{c}}}$。因此,以第1个阵元为参考阵元,则第n个阵元与参考阵元的相位差为:
| $\Delta {\psi _n} = \frac{{4\pi R\left( {n - 1} \right)\Delta f}}{{\rm{c}}} - \frac{{2\pi d}}{{{\lambda _0}}}\left( {n - 1} \right)\cdot \sin \theta \cos \varphi - \frac{{2\pi \Delta f}}{{\rm{c}}}{\left( {n - 1} \right)^2}d\sin \theta \cos \varphi {\rm{ }}$ | (3) |
${\lambda _0} = {\rm{c}}/{f_0}$为参考波长。如式(3)所示,第1项为距离和频率步进量的函数,第2项与传统相控阵相同,第3项为二次调制项。实际上,当频率步进量相比载频可以忽略不计时,第3项可忽略不计[18]。同样的,当频率步进量相比于载频可忽略时,地面散射体对应的归一化多普勒频率为ft≈$\frac{{2V}}{{{\lambda _0}{f\!_{\rm{r}}}}}\cos \theta \cos \varphi $。因此,第n个阵元第k个脉冲的接收信号可表示为:
| $\begin{array}{l} {x_{n,k}} \approx {\gamma _{\rm{p}}}\exp \left\{ { - {\rm{j}}\frac{{4\pi R\left( {n - 1} \right)\Delta f}}{{\rm{c}}}} \right.\quad \\ \quad \quad \left. { + {\rm{j}}2\pi \frac{d}{{{\lambda _0}}}\left( {n - 1} \right)\sin \theta \cos \varphi } \right\}\quad \quad \\ \quad \cdot \exp \left\{ {{\rm{j}}2\pi \frac{{2V}}{{{\lambda _0}f{_{\rm{r}}}}}\left( {k - 1} \right)\cos \theta \cos \varphi } \right\} \end{array}$ | (4) |
其中,gp为回波复散射系数。因此,FDA-STAP雷达对应的空时快拍可以表示为:
| $x \approx {\gamma _{\rm{p}}}{s_{\rm{t}}}\left( {f{_{\rm{t}}}} \right) \otimes {s_{\rm{s}}}\left( {f{_{\rm{s}}}} \right) \approx {\gamma _{\rm{p}}}{s_{\rm{t}}}\left( {f{_{\rm{t}}}} \right) \otimes \left[{{s_{\rm{R}}}\left( {{f_{\rm{R}}}} \right) \odot {s_{\rm{a}}}\left( {f{_{\rm{a}}}} \right)} \right]{\rm{ }}$ | (5) |
其中$\otimes$表示Kronecker乘积,⊙则表示Hadamard乘积;${\rm{ }}{{\rm{s}}_t} \in $CK×1,${\rm{ }}{{\rm{s}}_R} \in $CN×1和${\rm{ }}{{\rm{s}}_a} \in$ CN×1分别为时域导向矢量,距离导向矢量和方向导向矢量;${\rm{ }}{{\rm{s}}_s} \in $CN×1是由距离导向矢量和方向导向矢量构成的空域导向矢量[16]。机载雷达回波信号是由等距离环内杂波散射叠加而成,可表示为:
| $\begin{array}{*{20}{l}} {{x_{\rm{c}}} = \sum\limits_{m = 1}^M {\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{\gamma ^{\left\{ {i,m} \right\}}}{s_{\rm{t}}}\left( {f{_{\rm{t}}}^{\left\{ {i,m} \right\}}} \right) \otimes {s_{\rm{s}}}\left( {f{_{\rm{s}}}^{\left\{ {i,m} \right\}}} \right)} } }\\ {\;\;\;{\mkern 1mu} = \sum\limits_{m = 1}^M {\sum\limits_{i = 1}^{{N_{\rm{a}}}} {{\gamma ^{\left\{ {i,m} \right\}}}{s_{\rm{t}}}\left( {f{_{\rm{t}}}^{\left\{ {i,m} \right\}}} \right)} } }\\ {\;\;\;\;\;\; \otimes \left[{{s_{\rm{R}}}\left( {f{_{\rm{R}}}^{\left\{ m \right\}}} \right) \odot {s_{\rm{a}}}\left( {f{_{\rm{a}}}^{\left\{ {i,m} \right\}}} \right)} \right]} \end{array}$ | (6) |
其中Na为每个距离门内的统计独立的散射点数目,M为距离模糊数,本文中考虑M=2,即仅考虑无模糊距离区和模糊距离区的目标检测问题。上式中的i与m表示第m个距离模糊区的第i个散射点。
3 FDA-STAP雷达距离模糊杂波抑制方法由于频率分集引入的距离维可控自由度,FDA-STAP雷达中的空间频率是由方向频率和距离频率组成:
| ${f\!_{\rm{s}}} = {f\!_{\rm{R}}} + {f\!_{\rm{a}}} = - \frac{{2\Delta fR}}{{\rm{c}}} + \frac{d}{{{\lambda _0}}}\sin \theta \cos \varphi $ | (7) |
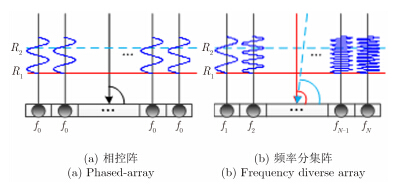
由式(7)可知空间频率依赖于距离和角度。图 2给出了传统相控阵和频率分集阵列的对比示意图。相控阵雷达的空间频率仅与角度有关,不随距离的变化而变化;而频率分集阵列的空间频率会随着距离和角度而变化,因此其等效的来波“角度”具有距离依赖性。图中红线与蓝线分别是距离为R1和R2的平面波波前。
|
图 2 FDA雷达波前示意图 Fig. 2 Illustration of the wavefront of the FDA radar |
对于特定方向和任意不同距离R1和R2的两个散射点,相应的空间频率可表示为:
| ${f\!_{\rm{s}}}\left( {{R_1}} \right) \! = \! {f\!_{\rm{R}}}\left( {{R_1}} \right) \! + \! {f\!_{\rm{a}}} \! = \! - \frac{{2\Delta f{R_1}}}{{\rm{c}}} \! + \! \frac{d}{{{\lambda _0}}}\sin \theta \cos \varphi $ | (8) |
| $ {f\!_{\rm{s}}}\left( {{R_2}} \right) \! = \! {f\!_{\rm{R}}}\left( {{R_2}} \right) \! + \! {f\!_{\rm{a}}} \! = \! - \frac{{2\Delta f{R_2}}}{{\rm{c}}} \! + \! \frac{d}{{{\lambda _0}}}\sin \theta \cos \varphi $ | (9) |
因此,相同方向的散射点,其空间频率差依赖于其距离差,即:
| $\begin{aligned} \Delta {f\!_{\rm{s}}}\left( {\Delta R} \right) & = {f\!_{\rm{s}}}\left( {{R_1}} \right) - {f_{\rm{s}}}\left( {{R_2}} \right) = {f\!_{\rm{R}}}\left( {{R_1}} \right) - {f\!_{\rm{R}}}\left( {{R_2}} \right) \\ & = - \frac{{2\Delta f\Delta R}}{{\rm{c}}} \end{aligned}$ | (10) |
其中ΔR=R1–R2。式(10)给出了空间频率差在给定方向和频率步进量时与距离差ΔR的关系。因此,在FDA-STAP雷达中会出现2次距离依赖问题。文献[16]提出了一种2次距离依赖补偿方法,克服了FDA-STAP雷达中杂波的2次距离依赖性。本文在此基础上提出了基于子空间投影的距离模糊杂波分离方法,在空间频率域实现距离模糊杂波的分离。实际上,对于前视FDA-STAP雷达,杂波的角度多普勒频率关系式可表示为:
| ${\left( {\frac{{{\lambda _0}}}{d}\left( {{f\!_{\rm{s}}} - {f\!_{\rm{R}}}} \right)} \right)^2} + {\left( {\frac{{{\lambda _0}{f\!_{\rm{r}}}}}{{2V}}{f\!_{\rm{t}}}} \right)^2} = {\cos ^2}\varphi $ | (11) |
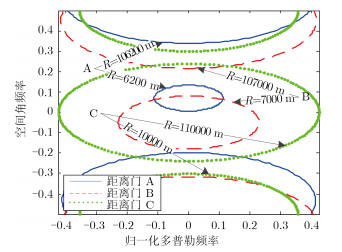
其中$\cos \varphi = \sqrt {1 - \frac{{{H^2}}}{{{R^2}}}} $。式(11)表明了杂波分布的椭圆耦合关系。当斜距变化时,椭圆曲线也会随着空间频率fR的变化而改变。此外,该椭圆会随着斜距的增大而增大。图 3给出了前视阵FDA-STAP雷达的杂波空时耦合关系曲线,图中给出了3个距离门的杂波空时耦合关系曲线,距离门A包含距离为6200 m和106200 m的回波,距离门B包含距离为7000 m和107000 m的回波,距离门C包含距离为10000 m和110000 m的回波,其他参数如第4节表 1所示。如图可见,杂波呈椭圆分布且随着距离增加而变大,此外,椭圆中心随着距离的变化在空间频率域发生变化。
|
图 3 FDA-STAP雷达空间-多普勒频率关系曲线 Fig. 3 Correlationship of the spatial and Doppler frequencies of the FDA-STAP radar |
不同于传统相控阵STAP雷达,FDA-STAP雷达的杂波分布在空间频率域会随斜距的变化而变化。因此,FDA-STAP雷达可以在空间频率域实现无模糊距离区杂波和模糊距离区杂波的区分。假定通过2次距离依赖补偿后,杂波在空间频率域明显分开,相应的补偿后的杂波数据为:
| ${x_{{\rm{comp}}}} = \sum\limits_{m = 1}^M {\sum\limits_{i = 1}^{{N_a}} {\gamma {s_{\rm{t}}}\left( {f{_{\rm{t}}}} \right) \otimes \widehat {{s_{\rm{s}}}}} \left( {\hat f{_{\rm{s}}}} \right)} $ | (12) |
其中,$\widehat {{s_{\rm{s}}}}\left( {\hat f{_{\rm{s}}}} \right) = {\rm{ }}h\left( {f{_{\rm{c}}}} \right) \odot {s_{\rm{s}}}\left( {f{_{\rm{s}}}} \right)$为补偿后的空域导向矢量,且相应的补偿矢量为:
| $h\left( {f{_{\rm{c}}}} \right) = {\left[{1,{{\rm{e}}^{ - {\rm{j}}2\pi {f_{\rm{c}}}}},\cdots ,{{\rm{e}}^{ - {\rm{j}}2\pi f{_{\rm{c}}}\left( {N - 1} \right)}}} \right]^{\rm{T}}}$ | (13) |
其中,补偿频率为${f\!_{\rm{c}}} = - \frac{{2\Delta f{R_{\rm{c}}}}}{{\rm{c}}}$,Rc为对应的斜距。补偿后的FDA-STAP雷达中杂波空间-多普勒频率耦合关系式可以表示为:
| ${\left( {\frac{{{\lambda _0}}}{d}\left( {{{\hat f}_{\rm{s}}} - \left( {{f_{\rm{R}}} - {f\!_{\rm{c}}}} \right)} \right)} \right)^2} + {\left( {\frac{{{\lambda _0}{f\!_{\rm{r}}}}}{{2V}}{f\!_{\rm{t}}}} \right)^2} = {\cos ^2}\varphi $ | (14) |
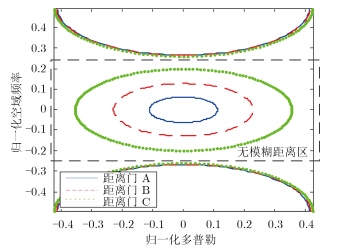
图 4给出了2次距离依赖补偿处理后的杂波空时耦合关系曲线,仿真参数与图 3相同。由图可见,经过2次距离依赖补偿处理后,在空间频率域中无模糊距离区和模糊距离区的杂波可以有效地区分。其中无模糊距离区杂波分布被对齐到低频区,而模糊距离区杂波分布被对齐到高频区。
|
图 4 2次距离依赖补偿后的空间多普勒频率耦合关系曲线 Fig. 4 Correlationship of spatial and Doppler frequencies after secondary range-dependence compensation |
为了进一步实现距离模糊杂波的有效分离,本文考虑基于子空间投影技术,构造空间频率域的投影矩阵和正交投影矩阵,并对回波数据进行矢量滤波,分别提取无模糊距离区的回波数据和模糊距离区的回波数据。构造空间频率域半正定矩阵为:
| $P = \int_{{{\tilde f}_{\rm{s}}} \in \left( { - \frac{1}{4},\frac{1}{4}} \right)} {{s_{\rm{s}}}} \left( {\tilde f{_{\rm{s}}}} \right)s_{\rm{s}}^{\rm{H}}\left( {\tilde f{_{\rm{s}}}} \right){\rm{d}}\tilde f{_{\rm{s}}}$ | (15) |
其中积分区间对应无模糊距离区域杂波在空间频率域的分布范围。实际上,为了有效地分离距离模糊杂波,对矩阵P进行奇异值分解,并构造列正交矩阵:
| $U = \left[{{u_1},{u_2},\cdots ,{u_I}} \right]$ | (16) |
其中,$\left\{ {{u_i}} \right\}_{i = 1}^I$为P矩阵I个大特征值对应的特征矢量。因此无模糊距离区域对应的投影矩阵可以表示为:
| ${\Pi _P} = {\rm{ }}U{U^{\rm{H}}}$ | (17) |
相应的正交投影矩阵表示为:
| $\Pi \mathop {{\text{ }}_P}\limits^ \bot = {I_N} - U{U^{\text{H}}}$ | (18) |
其中IN为N维单位矩阵。需要说明的是,正交投影矩阵对应的是模糊距离区的投影矩阵。因此,通过正交投影可有效地实现距离模糊杂波的分离,即:
| ${x_{{\rm{unambiguous}}}} = {\prod _P}{x_{{\rm{comp}}}}$ | (19) |
| ${x_{{\rm{ambiguous}}}} = {\rm{ }}\prod {P^ \bot }{x_{{\rm{comp}}}}$ | (20) |
距离模糊杂波分离后,需要进一步考虑杂波的距离依赖补偿问题。考虑采用多普勒补偿:
| $\widetilde {{x_\alpha }} = {x_\alpha } \odot g$ | (21) |
其中a=1表示无模糊距离区杂波,a=2表示模糊距离区杂波,$ {g} \! \in $CNK×1为补偿距离依赖性的多普勒弯曲矢量。例如,检测距离门的主杂波对应的多普勒频率为fd0,邻近距离门的主杂波对应的多普勒频率为fdl,则相应的多普勒弯曲矢量为:
| $\begin{array}{*{20}{l}} {g = \left[{1,\exp \left\{ {{\rm{j}}2\pi \left( {{f_{{\rm{d0}}}} - {f_{{\rm{d}}l}}} \right)} \right\},\cdots ,} \right.}\\ {\;\;\;\;\;\; \cdot {{\left. {\exp \left\{ {{\rm{j}}2\pi \left( {{f_{{\rm{d0}}}} - {f_{{\rm{d}}l}}} \right)\left( {K - 1} \right)} \right\}} \right]}^{\rm{T}}} \otimes {{\bf{1}}_N}} \end{array}$ | (22) |
其中,1N为全1的N维列矢量。经过子空间投影和多普勒弯曲补偿后的杂波分布近似满足同分布特性,对于无模糊距离区和模糊距离区可分别进行自适应杂波抑制和目标检测。
综上,当存在距离模糊时,传统相控阵雷达的STAP性能会严重下降。首先,由于距离模糊造成杂波非平稳性严重,使得杂波协方差矩阵估计所需的样本难以获得;其次,前视阵几何结构中,由于无模糊距离区与模糊距离区对应的杂波补偿互相制约,造成传统杂波谱补偿方法性能损失;最后,距离模糊引起杂波自由度大大增加,增加了系统杂波抑制的负担。本文所提FDA-STAP雷达在空间频率域实现了距离模糊杂波的分离,无模糊距离区和模糊距离区的杂波谱补偿不再互相制约,可以利用传统杂波谱补偿法实现杂波补偿和杂波抑制。
4 仿真实验本节通过仿真实验验证本文方法的有效性。表 1给出了相应的雷达系统仿真参数。
| 表 1 空中飞行目标环境目标关联正确次数 Tab. 1 Correct association time in air targets environment |
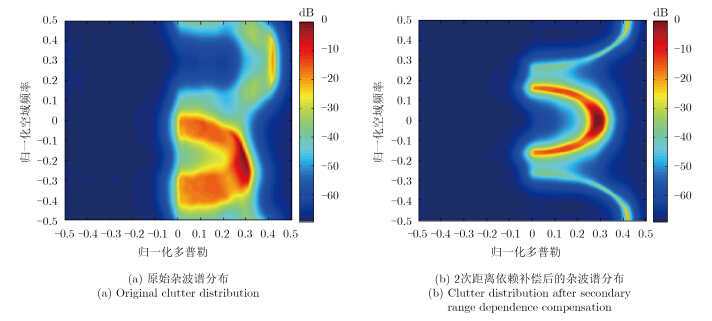
本实验中假设待检测目标位于无模糊距离区,图 5给出了FDA-STAP雷达杂波谱分布的仿真结果。由图可见,在FDA-STAP雷达中,无模糊距离杂波及模糊距离杂波在空间频率域可以被有效地区分。由于2次距离依赖性,原始杂波在空间频率域严重扩散,如图 5(a)所示。经过2次距离依赖补偿后,无模糊区杂波位于空间频率域的低频区,即[–1/4,1/4],而模糊距离区杂波分布在空间频率域的高频区,即[–1/2,–1/4]∪[1/4,1/2],如图 6(b)所示。
|
图 5 空时2维平面上的杂波谱分布特性 Fig. 5 Clutter spectra distribution in space-time domains |
|
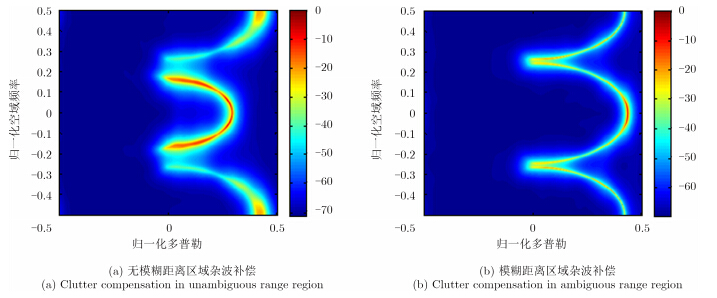
图 6 补偿后的空时2维杂波谱分布 Fig. 6 Clutter spectra distribution in space-time domains after compensation |
图 6给出了对无模糊区和模糊区杂波进行多普勒补偿后的杂波谱分布结果。如图所示,由于无模糊距离区杂波谱扩散严重,经过补偿后能够近似实现杂波的空时谱配准,此时,对于模糊距离区的杂波,由于补偿矢量的失配造成杂波谱扩散开来。此时,对无模糊距离区的目标进行自适应检测时,模糊距离区的杂波影响很小。类似地,进行模糊距离区杂波补偿时,无模糊距离区的杂波也一定程度地实现了配准,需要说明的是,此时对于无模糊距离区杂波的补偿是失配的。对于模糊距离区的目标进行检测时不会受到无模糊距离区杂波的影响。因此,FDA-STAP雷达能够有效地区分无模糊距离区和模糊距离区的杂波,并分别进行杂波抑制和目标检测。
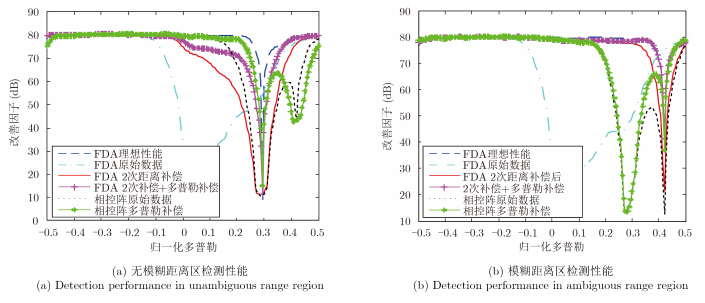
4.2 目标检测性能分析图 7给出了杂波抑制改善因子随多普勒的变化曲线。图 7(a)为无模糊距离区检测性能曲线,图 7(b)为模糊距离区检测性能曲线。由图可见,对于传统相控阵STAP雷达,多普勒补偿对于无模糊距离区和模糊距离区的杂波补偿互相制约。对于无模糊距离区的目标检测,无模糊距离区杂波扩散严重,模糊距离区扩散相对微弱。经多普勒补偿,无模糊距离区杂波的距离依赖性得到补偿,模糊距离区的杂波反而严重扩散。对于FDA-STAP雷达,基于原始数据的信号处理性能损失严重,经过2次距离依赖补偿和多普勒补偿后的性能大大提高。需要说明的,传统STAP雷达改善因子性能在模糊距离区主瓣杂波和无模糊距离区主瓣杂波的性能下降严重。FDA-STAP雷达中,由于杂波在空间频率域实现了分离,因此,对于无模糊距离区目标检测,改善因子仅在无模糊距离区主瓣杂波处存在凹口;对于模糊距离区目标检测,改善因子仅在模糊距离区主瓣杂波处存在凹口。
|
图 7 改善因子随多普勒的变化曲线 Fig. 7 Improvement factor versus Doppler frequency |
本文给出了FDA-STAP雷达信号模型,提出了一种距离模糊杂波抑制方法。利用频率分集阵列发射导向矢量的距离角度依赖性,并结合子空间投影方法,在空间频率域可以有效地分离距离模糊杂波。将杂波分离技术与传统杂波谱补偿方法相结合,显著提升了距离模糊杂波抑制的性能。由于FDA-STAP雷达能够在空间频率域将无模糊距离区杂波与模糊距离区杂波分开,因此能有效提高非均匀杂波抑制性能。
| [1] | Klemm R. Principles of space-time adaptive processing[J]. Electronics & Communication Engineering Journal, 2002, 14(6): 295-296.( 1) 1) |
| [2] | Guerci J R. Space-Time Adaptive Processing for Rada[M]. Norwood, MA: Artech House, 2003, Chapter 1-10.( 1) 1) |
| [3] | Klemm R. Comparison between monostatic and bistatic antenna configurations for STAP[J]. IEEE Transactions on Aerospace and Electronic System, 2000, 36(2): 596-608.( 1) 1) |
| [4] | Borsari G. Mitigating effects on STAP processing caused by an inclined array[C]. Proceedings of the 1998 IEEE Radar Conference, Dallas, 1998: 135-140.( 1) 1) |
| [5] | Kreyenkamp O and Klemm R. Doppler compensation in forward-looking STAP Radar[J]. IEE Proceedings-Radar, Sonar and Navigation, 2001, 148(5): 253-258.( 1) 1) |
| [6] | Himed B, Zhang Y, and Hajjari A. STAP with angle-Doppler compensation for bistatic airborne radars[C]. Proceedings of the IEEE Radar Conference, Long Beach, 2002: 311-317.( 1) 1) |
| [7] | Melvin W L, Himed B, and Davis M E. Doubly adaptive bistatic clutter filtering[C]. Proceedings of the 2003 IEEE Radar Conference, Hunstville, 2003: 171-178.( 1) 1) |
| [8] | Melvin W L and Davis M E. Adaptive cancellation method for geometry-induced nonstationary bistatic clutter environments[J]. IEEE Transactions on Aerospace and Electronic System, 2007, 43(2): 651-672.( 1) 1) |
| [9] | Pearson F and Borsari G. Simulation and analysis of adaptive interference suppression for bistatic surveillance radars[C]. Adaptive Sensor Array Processing Workshop, MIT Lincoln Laboratory, Lexington, 2001: 13-14.( 1) 1) |
| [10] | Lapierre F D, Ries P, and Verly J G. Foundation for mitigating range dependence in radar space-time adaptive processing[J]. IET Radar, Sonar & Navigation, 2009, 3(1): 18-29.( 1) 1) |
| [11] | Ries P, Lapierre F D, and Verly J G. Geometry-induced range-dependence compensation for bistatic STAP with conformal arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 275-294.( 1) 1) |
| [12] | Varadarajan V and Krolik J L. Joint space-time interpolation for distorted linear and bistatic array geometries[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 848-860.( 1) 1) |
| [13] | Hale T B, Temple M A, Raquet J F, et al.. Localized three-dimensional adaptive spatial-temporal processing for airborne radar[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(1): 18-22.( 1) 1) |
| [14] | Hale T B, Temple M A, and Wicks M C. Clutter suppression using elevation interferometry fused with space-time adaptive processing[J]. Electronic Letters, 2001, 37(12): 793-794.( 1) 1) |
| [15] | Baizert P, Hale T B, Temple M A, et al.. Forward-looking radar GMTI benefits using a linear frequency diverse array[J]. Electronics Letters, 2006, 42(22): 1311-1312.( 1) 1) |
| [16] | 王伟伟, 吴孙勇, 许京伟, 等. 基于频率分集阵列的机载雷达距离模糊杂波抑制方法[J]. 电子与信息学报, 2015, 37(10): 2321-2327.Wang Wei-wei, Wu Sun-yong, Xu Jing-wei, et al.. Range ambiguity clutter suppression for airborne radar based on frequency diverse array[J]. Journal of Electronics & Information Technology, 2015, 37(10): 2321-2327.( 4) 4) |
| [17] | Sammartino P F and Backer C J. Developments in the frequency diverse bistatic system[C]. IEEE Radar Conference, Pasadena, 2009: 1-5.( 1) 1) |
| [18] | Sammartino P F, Backer C J, and Griffiths H D. Frequency diverse MIMO techniques for radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 201-222.( 1) 1) |
| [19] | Antonik P, Wicks M C, Griffiths H D, et al.. Multi-mission multi-mode waveform diversity[C]. 2006 IEEE conference on Radar, Verona, NY, 2006, DOI: 10.1109/RADAR. 2006.1631858.( 1) 1) |


