1 引言
传统的杂波抑制算法主要包括DPCA(Displaced Phase Center Antenna,DPCA)技术[1, 2],ATI(Along Track Interferometry,ATI)技术[3, 4, 5]以及空时自适应处理 (Space-Time Adaptive Processing,STAP)技术[6]。对于多通道SAR系统,传统算法中的绝大部分要求每个通道接收到杂波回波不存在多普勒谱模糊。然而,对于具有GMTI能力的HRWS MC-SAR系统,其单个通道接收到杂波回波是存在多普勒模糊。虽然文献[7]提出的方法可以对HRWS MC-SAR系统进行杂波抑制,但其要求通道数必须大于多普勒模糊数的两倍且DPCA条件必须严格满足,这将明显地增加系统复杂度。本文针对具有GMTI能力的HRWS MC-SAR系统,提出了一种新颖的杂波抑制算法。在每个通道回波存在多普勒谱模糊时,利用方位的CFT (Chirp-Fourier Transform,CFT)[8]操作来对每个通道回波的方位信号进行压缩。因此,可以在距离脉压方位CFT域(RC-CFT domain)中获得每个通道回波的粗聚焦SAR图像。通常,在杂波抑制之前,动目标参数是未知的。为了在杂波抑制过程中对所有的动目标尽可能保持最大能量,假设动目标处在动目标区域的中间位置(动目标区域定义为相邻两个杂波模糊分量之间的区域)。接着,针对所有动目标区域,构造出一系列空域滤波器,同时在杂波方向形成零点。利用构造的空域滤波器,对杂波进行抑制和提取动目标回波信号。
经过杂波抑制之后,动目标成像处理是另外一个重要的问题,其包括动目标参数估计,特别是斜距速度估计。在本文中,提出了一种新的动目标成像算法。在距离频率域对每个通道回波沿方位向进行CFT之后,QRCM (Quadratic Range Cell Migration,QRCM)得到有效地校正并只存在动目标的线性RCM (Range Cell Migration)。在本文中,首先将动目标回波变换到距离频率方位时域。接着,沿距离频率方向构造两组信号和利用文献[9]所提出算法进行基带多普勒中心估计。利用多视互相关的多普勒中心模糊数求解方式[10]来获得准确的动目标斜距速度和对动目标线性RCM进行有效地校正。最后,经过方位逆傅里叶变换之后,可以获得聚焦好的动目标图像。
本文内容安排如下:第2节给出了HRWS MC-SAR系统的几何关系;第3节推导了动目标和杂波的粗聚焦图像及复响应;第4节介绍了杂波抑制和动目标检测方法;第5节给出了动目标成像和斜距速度估计方法;第6节对实测的动目标HRWS MC-SAR数据进行了处理;第7节对全文进行了总结。
2 HRWS MC-SAR系统的几何关系
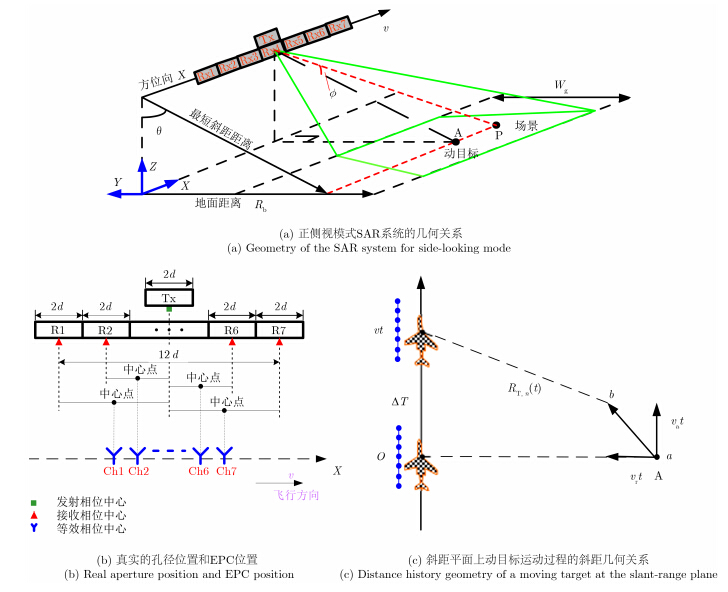
对于正侧视模式,HRWS SAR系统的几何关系如图 1(a)所示,其中X轴为方位方向,其表示平台的速度方向,Y轴指向左边,Z轴方向背离地球中心。雷达平台以恒定前向速度v沿方位向运动,q为俯仰角,f为锥角,${W_{\rm{g}}}$为测绘带宽度,${R_{\rm{b}}}$为地距。通常,把整个天线沿方位分割成N个子孔径,其如图 1(b)所示且以7个通道为例,即N=7。中间的子孔径天线发射宽波束的线性调频信号,所有的子孔径天线同时接收回波信号。每相邻两个子孔径天线沿方位的距离为2d。HRWS MC-SAR系统中高的方位分辨率由单个子孔径天线尺寸决定的,而利用整个天线的长度来抑制多普勒谱模糊。通过补偿一个常数相位,每一组分开的发射和接收通道可以等效于一个对应于等效相位中心(Effective Phase Center,EPC)的通道自发自收。对于EPC位置,相邻的通道之间的间距为d。令${d_n} = n \cdot d$为第n通道和参考通道之间的EPC位置距离($n = 1,2,\cdots ,N$)。在本文中,将第1个通道作为参考通道。
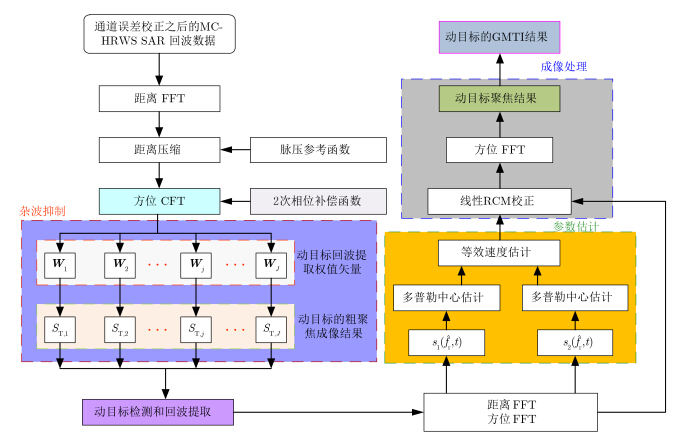
在HRWS MC-SAR 系统数据的录取过程中,假设动目标以恒定速度运动。图 1(c)为正侧视模式下平台与动目标在斜距平面上的几何关系,其中vr与va分别表示动目标在径向方向和沿航向方向的速度。t表示方位慢时间,R0为雷达平台与动目标之间(或是成像场景中杂波与雷达平台之间)的最短斜距,RT,n(t)为第n通道与动目标之间的瞬时斜距。在雷达的观测时间Ta内,动目标由a点位置运动到b点位置。本文主要讨论HRWS MC-SAR系统中有关动目标的杂波抑制和成像处理。图 2 所示为本文所提出算法的流程图,其主要步骤包括杂波抑制、参数估计和成像处理。此外,Wj为提取动目标回波的权值矢量,ST,j为动目标粗聚焦的图像,${s_1}\left( {{{\hat f}_{\rm r}},t} \right)$和${s_2}\left( {{{\hat f}_{\rm r}},t} \right)$为估计多普勒参数构造的两组数据。
3 动目标和杂波的粗聚焦图像及复响应
CFT作为FT的2阶推广,比原始的FT具有更好处理线性调频信号的能力。信号s(t)的CFT可以表示为[8]:
|
$\begin{align}
S\left( {{f \! _{\rm a}}} \right) = & \int {s\left( t \right)\exp \left\{ { - {\rm{j}}\left( {{{\varphi _{_0}}} + 2{π} {f_1}t + {π} {k_{\rm a}}{t^2}} \right)} \right\}} \\
& \cdot \exp \left( { - {\rm{j}}2{π} {f_{\mathop{\rm a}\nolimits} }t} \right){\rm{d}}t
\end{align}$
|
(1)
|
其中
j0为常数相位,
f1为CFT频率谱的平移,
ka为分析信号采用的线性调频斜率,
fa为CFT的频率。在式(1)中,CFT可以认为是信号
s(
t)经过一个2次多项式相位$\exp \left\{ { - {\rm{j}}\left( {{\varphi _0} + 2{π} {f_1}t + {π} {k_{\rm a}}{t^2}} \right)} \right\}$补偿之后的FT。式(1)对应的CFT逆变换可以表示为:
|
$\begin{align}
s\left( t \right) = & \frac{1}{{2{π} }}\int {S\left( {{f \! _{\rm a}}} \right)\exp \left\{ {{\rm{j}}\left( {{\varphi _0} + 2{π} {f_1}t + {π} {k_{\rm a}}{t^2}} \right)} \right\}} \\
& \cdot \exp \left( {{\rm{j}}2{π} {f \! _{\rm a}}t} \right){\rm{d}}{f \! _{\rm a}}
\end{align}$
|
(2)
|
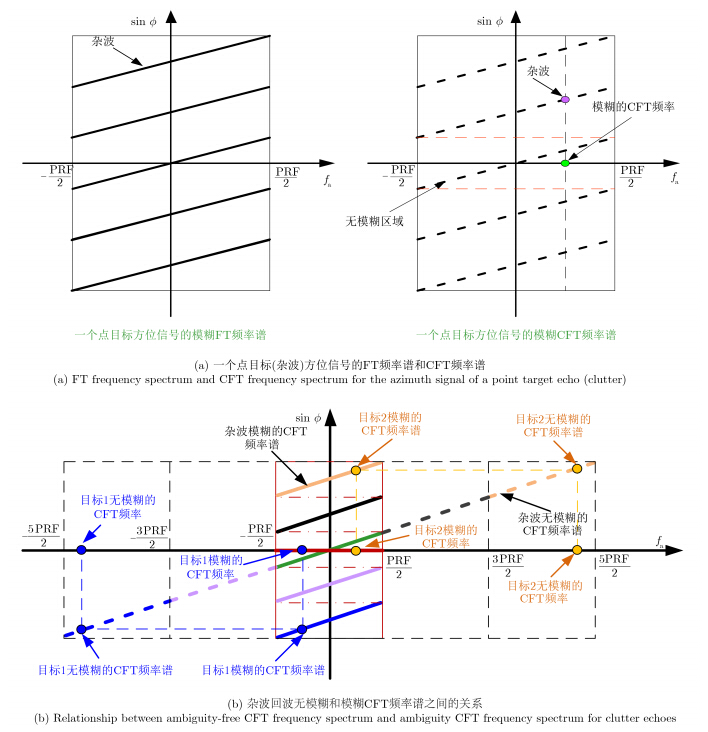
一个点目标方位信号的CFT频率谱仅仅分布在几个频率单元,这与傅里叶频率谱存在很大区别。此外,CFT频率fa和锥角之间的关系可以表示为${f_{\rm{a}}} = \frac{{2v\sin \phi }}{\lambda }$。图 3(a)所示为一个点目标方位信号的FT频率谱和CFT频率谱,其中多普勒带宽大于PRF。从图中可以看到模糊的FT频率谱分布到整个多普勒频率区域$\left[{ - \frac{{{\mathop{\rm PRF}\nolimits} }}{2},\frac{{{\mathop{\rm PRF}\nolimits} }}{2}} \right]$,而相应的CFT频率谱仅仅分布在一些CFT频率单元。然而,一个点目标CFT频率谱的模糊特性意味着位置模糊,如图 3(b)所示。图 3(b)为杂波的模糊CFT频率谱和无模糊CFT频率谱之间关系,其中宽的虚线代表杂波无模糊的CFT频率谱,宽实线为杂波模糊的CFT频率谱。图 3(b)是以两个点目标(杂波)为例。
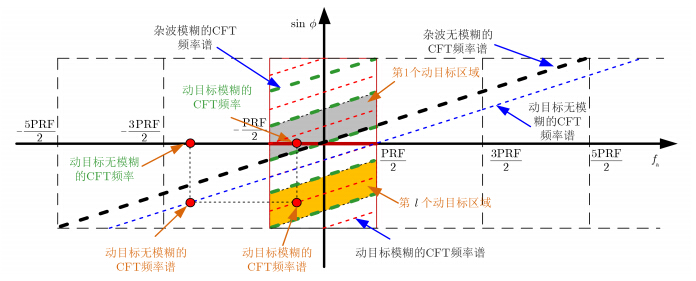
图 4所示为动目标方位信号的CFT频谱,其中黑的宽虚线表示杂波无模糊的CFT频率谱,蓝色细虚线为动目标无模糊CFT频率谱。绿色宽的虚线和红色细虚线分别表示杂波和动目标模糊的CFT频率谱。此外,动目标区域定义为两个杂波模糊分量之间的区域,图 4所示为第1个动目标区域和第l个动目标区域。动目标CFT频率谱位于动目标区域。每个通道杂波回波的粗聚焦图像位于所有CFT频率单元及其相应的模糊分量。在杂波抑制和动目标检测过程中,要求所有杂波方向得到抑制而动目标区域方向能量尽可能地保持。
4 杂波抑制和动目标检测
在文献[11]中,利用多个多普勒方向约束方式来抑制多普勒模糊分量和重构方位多普勒无模糊信号,其在多普勒模糊分量方向上形成零点。受多个多普勒方向约束方式的启发,为了在CFT频率域中对杂波进行抑制,零点可以在杂波方向及其相应的模糊方向上形成。此外,动目标潜在区域的能量需要得到保持(在CFT频率域中,由于动目标位于动目标区域如图 4所示,动目标潜在方向表示动目标区域方向)。因此,杂波抑制的最优准则可以表示为:
|
$\begin{array}{*{20}{l}}
{\mathop {\min }\limits_{{W_{\rm{l}}}} W_{\rm{l}}^{\rm{H}}\left( {{f_{\rm{a}}}} \right){R_{\rm{X}}}\left( {{f_{\rm{a}}}} \right){W_{\rm{l}}}\left( {{f_{\rm{a}}}} \right)}\\
{{\rm{s}}.{\rm{t}}\;W_{\rm{l}}^{\rm{H}}\left( {{f_{\rm{a}}}} \right)C = Q}
\end{array}\} $
|
(3)
|
在式(3)中,当动目标存在时,
RX(
fa)为在CFT频率单元
fa的多通道输出对应的协方差矩阵,即
RX(
fa)可以表示为:
|
${R_X}({f_a}) = E[({S_c}({f_a}) + {S_T}({f_a})){({S_c}({f_a}) + {S_T}({f_a}))^H}]$
|
(4)
|
在杂波的抑制过程中,杂波及其模糊分量方向是已知的且需要形成零点。接着,可以得到导向矢量矩阵:
|
$C = [{a_{T,l}}({f_a}),{a_{c, - L}}({f_a}), \cdots ,{a_{c,l}}({f_a}), \cdots ,{a_{c,L}}({f_a})]$
|
(5)
|
式(5)中,对于CFT频率单元
fa,${f_a},{a_{{\rm{T}},1}}({f_a}){\rm{ }} = {\Gamma _T} \cdot {a_{c,l}}({f_a})$ 为动目标方向(通常,在动目标参数估计之前,动目标方向是未知的。为了在杂波抑制过程中对所有动目标保持高的信号能量,认为动目标位于动目标区域的中间位置),
ac,l(
fa)为杂波方向及其模糊分量方向。通常,动目标方向需要尽可能保持最大能量和杂波方向及其模糊分量方向需要保持尽可能的最小能量,由此可以得到${Q} = {\bigg[{1 \underbrace {0 \ 0 \ \cdots \ 0}_{2L + 1}} \bigg]^{\rm H}}$。
Wl(
fa)为在CFT频率谱中提取位于第
l个动目标区域动目标的权值矢量。式(3)所示最优化问题的最优解可以表示为:
|
$ {W}_{\rm l}^{\rm opt}\left( {{f \! _{\rm a}}} \right) = {R}_{\rm X}^{ - 1}{C}{\left( {{{C}^{\rm{H}}}{R}_{\rm X}^{ - 1}{C}} \right)^{ - 1}}{Q}$
|
(6)
|
包含动目标的多通道SAR系统回波信号为
Sc(
fa)+
ST(
fa)。假设动目标的CFT频率谱位于动目标的第
l个区域位置,如
图 5所示。杂波抑制过程可以表示为:
|
${{\hat S}_{{\rm{T}},{\rm{l}}}}\left( {{f_{\rm{a}}}} \right) = {\left[ {W_{\rm{l}}^{{\rm{opt}}}\left( {{f_{\rm{a}}}} \right)} \right]^{\rm{H}}} \cdot \left( {{S_{\rm{c}}}\left( {{f_{\rm{a}}}} \right) + {S_{\rm{T}}}\left( {{f_{\rm{a}}}} \right)} \right)$
|
(7)
|
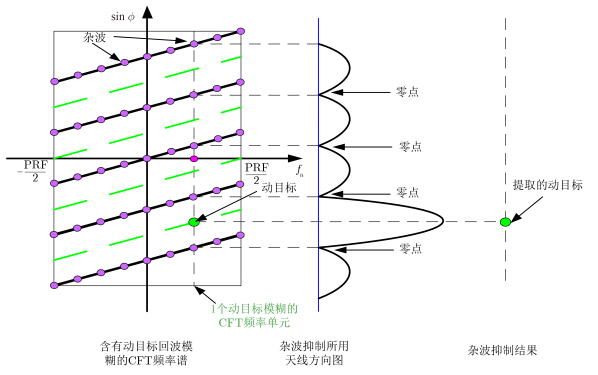
图 5所示为杂波抑制过程,其中在成像场景中包含一个动目标。从图中看到在杂波方向及其模糊分量方向上形成零点。经过杂波抑制之后,可以提取出动目标回波。
当动目标多普勒中心fdc满足${f_{\rm dc}} = {K_{\rm dc}} \cdot {\mathop{\rm PRF}\nolimits} $,动目标的CFT频率谱和杂波的CFT频率谱处在相同位置区域,其将在杂波抑制过程中同样也得到抑制。由于${v_{\rm PRF}} \! = \! \frac{{{\mathop{\rm PRF}\nolimits} \cdot \lambda }}{2}$和${f_{\rm dc}} \! = \! \frac{{2{v_{\rm r}}}}{\lambda }$,${v_{\rm r}} \! = \! {K_{\rm dc}} \! \cdot \! {v_{\rm PRF}}$,其中vr为盲速。注意到当系统的PRF越低,更多的斜距速度将位于盲速位置。
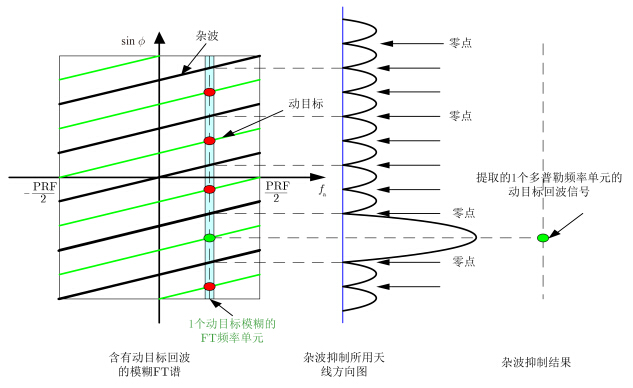
图 6 所示为ISTAP[12, 13, 14]方式的杂波抑制处理过程和动目标信号提取。在图 6中注意到当动目标的1个信号分量需要从1个多普勒频率单元提取出来时,所有杂波方向和动目标模糊分量方向需要形成零点。经过在每个多普勒频率单元提取动目标信号分量和重排之后,可以得到动目标无模糊的多普勒谱。由于动目标多普勒谱的模糊数和杂波一样,因此所需的通道数至少应为杂波谱模糊数的两倍。然而,对于本文所提出的杂波抑制算法,需要的通道数只需大于杂波的模糊数。
5 动目标成像和斜距速度估计
在这一小节中,将对动目标的成像算法进行讨论,其包括动目标斜距速度估计。经过杂波抑制之后,对提取的动目标回波进行距离FT和方位逆FT。动目标回波可以表示为:
|
$\begin{align}
{s_{\rm T}}\left( {{f_{\rm r}},t} \right) \! = & {\sigma _{\rm T}}{G_{\rm L}}{W_{\rm r}}\left( {{f_{\rm r}}} \right){w_{\rm az}}\left( {t - {t_{\rm T}}} \right)\\
& \! \cdot \exp \! \left\{ { - {\rm{j}}\frac{{4{π} }}{{\rm{c}}}\left( {{f_{\rm c}} + {f_{\rm r}}} \right){v_{\rm r\_equ}}\left( {t - {t_0}} \right)} \right\}\\
& \! \cdot \exp \! \left\{ { \! - {\rm{j}}\frac{{4{π}}}{{\rm{c}}}\left( {{f_{\rm{c}}} \! + \! {f_{\rm{r}}}} \right) \! \left( {{\rm{ }}{R_{{\rm{equ}}\_{\rm{T}}}} \! + \! {v_{\rm{r}}}\left( {{t_0} \! - \! {t_{\rm{T}}}} \right)} \right)} \! \right\}
\end{align}$
|
(8)
|
其中${v_{\rm r\_equ}} = {v_{\rm r}} + \frac{{{v^2}}}{{{R_0}}}\left( {{t_0} - {t_{\rm T}}} \right)$为等效斜距速度,
GL为杂波抑制过程中动目标能量损失。
图 7所示为对提取的动目标回波进行构造的两组信号,其中整个矩形区域为在距离频率方位时域的整个动目标回波,红色区域为构造得到的第1组回波信号,蓝色区域为构造得到的第2组回波信号。利用已有的多普勒中心估计算法
[9],可以估计出两组信号的多普勒中心。令${\hat f_{\rm dc\_1}}$和${\hat f_{\rm dc\_2}}$分别为${s_1}\left( {{{\hat f}_{\rm{r}}},t} \right)$和${s_2}\left( {{{\hat f}_{\rm r}},t} \right)$估计得到的多普勒中心。在多普勒中心估计过程中,利用每一组回波的所有距离频率单元来估计相应的多普勒中心。由于基带的多普勒中心和距离频率的关系是线性的,估计得到的多普勒中心对应于每组信号中间距离频率。因此,可以得到:
|
${\hat f_{\rm dc\_1}} = \frac{{2{v_{\rm r\_equ}}}}{{\rm{c}}}\left( {{f_{\rm c}} - \frac{B}{4}} \right) - {M_{\rm amb}} \cdot {\mathop{\rm PRF}\nolimits} $
|
(9)
|
|
${\hat f_{{\rm{dc\_2}}}} = \frac{{2{v_{\rm r\_equ}}}}{{\rm{c}}}\left( {{f_{\rm c}} + \frac{B}{4}} \right) - {M_{\rm amb}} \cdot {\mathop{\rm PRF}\nolimits} $
|
(10)
|
其中
Mamb为多普勒中心模糊数。基于多视互相关的多普勒中心解模糊算法
[10],可以得到等效的斜距速度
vr_equ:
|
${\hat v_{\rm r\_equ}} = \frac{{\left( {{{\hat f}_{\rm dc\_2}} - {{\hat f}_{{\mathop{\rm dc}\nolimits} \_1}}} \right) \cdot {\rm{c}}}}{B}$
|
(11)
|
接着,估计得到斜距速度${\hat v_r}$:
|
${\hat v_{\rm r}} = \frac{{\left( {{{\hat f}_{\rm dc\_2}} - {{\hat f}_{{\mathop{\rm dc}\nolimits} \_1}}} \right) \cdot {\rm{c}}}}{B} - \frac{{{v^2}}}{{{R_0}}}\left( {{t_0} - {t_{\rm T}}} \right)$
|
(12)
|
线性RCM校正函数可以构造为:
|
${H_2}\left( {{f_{\rm r}},t} \right) = \exp \left\{ {{\rm{j}}\frac{{4{π} }}{{\rm{c}}}{f_{\rm r}} \cdot {{\hat v}_{\rm r\_equ}}\left( {t - {t_0}} \right)} \right\}$
|
(13)
|
经过距离逆傅里叶变换和方位傅里叶变换,聚焦的动目标图像可以表示为:
|
$\begin{align}
{s_{\rm T}}\left( {\hat t,{f \! _{\rm a}}} \right) = & {\sigma _{\rm T}}{G_{\rm L}}{G_{\rm r}}{G_{\rm az}}\\
& \cdot {\mathop{\rm sinc}\nolimits} \left( \! {B\left( \! {\hat t - \frac{{2\left( {{R_{\rm equ\_T}} \!+\! {v_{\rm r}}\left( {{t_0} \!-\! {t_{\rm T}}} \right)} \right)}}{{\rm{c}}}} \! \right)} \right)\\
& \cdot {\mathop{\rm sinc}\nolimits} \left( {{T_{\rm a}}\left( {{f \! _{\rm a}} - \frac{{2 \cdot {f_{\rm c}} \cdot {v_{\rm r\_equ}}}}{{\rm{c}}}} \right)} \right)\\
& \cdot \exp \left( { - {\rm{j}}2{π} \left( {{f \! _{\rm a}}{t_{\rm T}} - \frac{{2{f_{\rm c}}{t_0}}}{{\rm{c}}}} \right)} \right)
\end{align}$
|
(14)
|
从式(14)中,注意到利用方位全孔径回波信号可以获得方位全孔径分辨率。对于几何分辨率,其方位分辨率为$\frac{v}{{{B_{\rm a}}}} = \frac{v}{{{k_{\rm a}} \cdot {T_{\rm a}}}}$,其中Ba为方位多普勒带宽,ka为方位调频率,距离分辨率为$\frac{{\rm{c}}}{{2B}}$。
6 实测的动目标HRWS MC-SAR数据
在这一小节中,将讨论在实测的机载HRWS MC-SAR数据中动目标的处理结果。在实验过程中,录取得到实测的机载X波段的HRWS MC-SAR数据,其包括动目标回波,主要的系统参数如表 1所示。在系统的工作过程中,中间通道发射线性调频信号,所有通道接收场景回波信号。由于多普勒带宽为1000 Hz和多通道系统的PRF为200 Hz,对于杂波回波的方位多普勒信号其多普勒模糊数近似为5。此外,在数据的录取过程中成像场景包括多个动目标。
表 1(Tab.1)
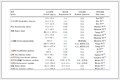
表 1 实测数据的系统参数Tab.1 System parameters for the real data
| 脉冲宽度 | 10µs | PRF | 200Hz |
| 发射信号带宽 | 180MHz | 通道数 | 7 |
| 采样率 | 240MHz | 多普勒带宽 | 980Hz |
| 波长 | 0.033 | 平台速度 | 111m/s |
|
表 1 实测数据的系统参数
Tab.1 System parameters for the real data |
对于获得的HRWS MC-SAR回波,利用文献[11]提出的HRWS MC-SAR成像算法来重构杂波方位多普勒无模糊信号。进而得到杂波聚焦的成像结果,如图 8所示。从图 8中,可以看到两个动目标及模糊分量信号,其分别由红色实圆圈和绿色虚圆圈标出。通常,利用传统的HRWS MC-SAR成像算法[11]进行处理,动目标无法取得很好聚焦效果。为了对动目标进行聚焦处理,利用本文所提出的杂波抑制和动目标成像处理算法来提取和重新聚焦动目标回波。
在动目标回波的提取过程中,首先进行杂波抑制,其过程如图 9所示。图 9(a)所示为录取的HRWS MC-SAR系统单通道回波在RC-CFT域的信号形式,其中两个动目标的回波被标出来,且杂波回波具有高的幅度能量值。接着,得到杂波的抑制结果,如图 9(b)所示,杂波得到抑制,动目标回波得到保留。为了进一步说明杂波抑制性能,提取出line 1和line 2在图 9(a)和图 9(b)中的信号进行比较。图 9(c)所示为line 1所标出信号的比较结果,其中红色虚线为杂波抑制之前的信号,黑色实线为杂波抑制之后的信号。图 9(d)所示为line 2所标出信号的比较结果。从图 9(c)和图 9(d)中注意到在假设动目标能量不变的情况下杂波可以抑制15 dB,这说明本文所提出的杂波抑制算法是有效的。
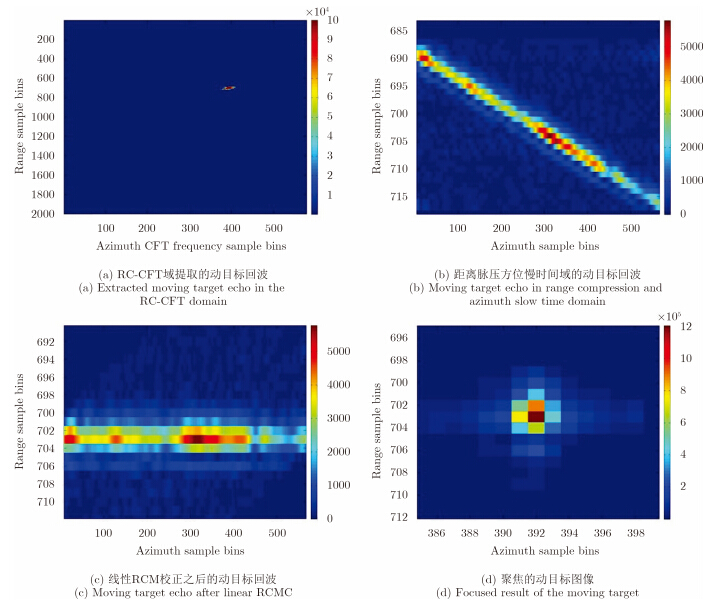
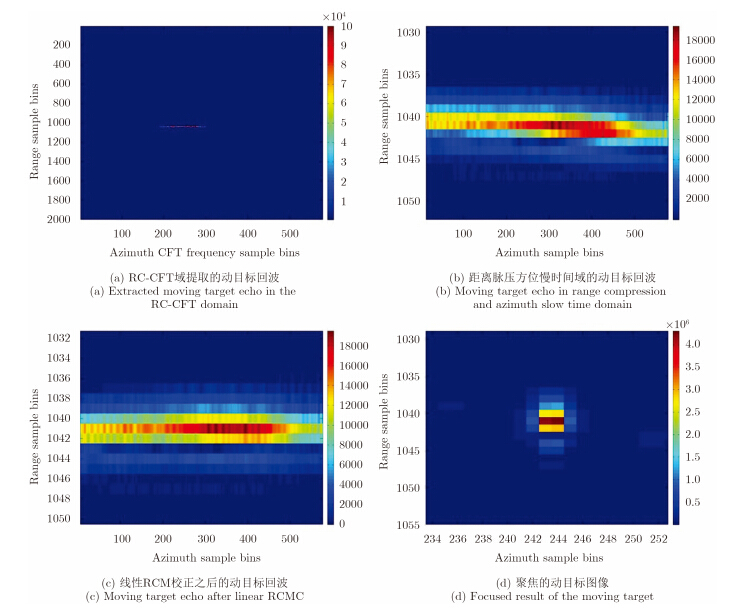
经过杂波抑制之后,可以提取出动目标回波。图 10(a)所示为提取出来在CR-CFT域中第1个动目标(Target 1)回波信号,图 10所示为第1个动目标的成像过程。图 10(b)所示为该提取动目标回波在距离脉压和方位慢时间域的信号形式,其存在明显的RCM。经过参数估计和线性RCM校正之后,回波如图 10(c)所示,估计得到动目标斜距速度为7.2063 m/s。图 10(c)中,动目标的回波校正到一条水平直线上,这说明估计得到的斜距速度是准确的。图 10(d)所示为聚焦的动目标图像。类似地,第2个动目标(Target 2)的成像处理过程如图 11所示,且聚焦好的动目标图像如图 11(d)所示。因此,对于HRWS MC-SAR系统,本文所提出的动目标成像算法是有效的。
7 结束语
利用沿方位的多通道自由度进行多普勒模糊分量抑制,允许多通道雷达系统获取高分辨宽测绘带成像。同样,杂波抑制使得人们可以进行动目标检测和成像处理。在本文中,主要研究了具有GMTI功能的HRWS MC-SAR系统。HRWS MC-SAR系统中每个通道杂波回波存在多普勒模糊,传统的杂波抑制算法,如DPCA,EDPCA及基于STAP的杂波抑制算法,不能取得很好的杂波抑制性能。因此,针对HRWS MC-SAR系统,本文提出了一种稳健的杂波抑制算法。经过杂波抑制之后,利用基于CFAR和GLRT检测器可以将动目标回波提取出来,进而完成对动目标的聚焦处理。本文所提出的算法仅要求通道数大于杂波谱的多普勒模糊数。与此同时,所提出算法不仅适用于均匀的DPC采样,同样也适用于非均匀采样。然而,本文所提方法对于盲速动目标是无能为力的,与常规STAP方法一样,在空时平面中,盲速动目标的空时谱分布与静止背景杂波是重合的,在抑制杂波的同时,动目标能量也会被抑制掉。最后,实测数据处理结果验证了本文所提算法的有效性。



 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 1)
1) 2)
2) 2)
2) 2)
2) 3)
3) 3)
3) 3)
3) 3)
3)

