«上一篇
文章快速检索     高级检索
下一篇»
  雷达学报  2015, Vol. 4 Issue (3): 361–366  DOI: 10.12000/JR15052
0

引用本文 [复制中英文]

杨谦, 魏兵, 李林茜, 等. DGTD用于RCS计算的初步研究[J]. 雷达学报, 2015, 4(3): 361–366. DOI: 10.12000/JR15052.
[复制中文]
Yang Qian, Wei Bing, Li Lin-qian, et al.. Preliminary research on RCS using DGTD[J].Journal of Radars, 2015, 4(3): 361–366.: 10.12000/JR15052.
[复制英文]

基金项目

国家自然科学基金项目(61231003, 61401344)资助课题

通信作者

魏兵 bwei@xidian.edu.cn

作者简介

杨 谦(1989–)，男，博士研究生，主要研究方向为计算电磁学。 E-mail: zijiangy@126.com
魏 兵(1970–)，男，教授，博士，主要研究方向为电磁理论、复杂系统中的场与波和计算电磁学等。 E-mail: bwei@xidian.edu.cn
李林茜(1985–)，男，博士研究生，主要研究方向为计算电磁学。 E-mail: 395106835@qq.com

文章历史

收稿：2015-05-05
改回：2015-06-16
Contents              Abstract              Full text              Figures/Tables              PDF
DGTD用于RCS计算的初步研究
杨 谦①②, 魏 兵①② , 李林茜①②, 葛德彪①②    
① 西安电子科技大学物理与光电工程学院 西安 710071
② 西安电子科技大学信息感知技术协同创新中心 西安 710071
2015-05-05收到
基金项目： 国家自然科学基金项目(61231003, 61401344)资助课题
作者简介：杨 谦(1989–)，男，博士研究生，主要研究方向为计算电磁学。 E-mail: zijiangy@126.com
魏 兵(1970–)，男，教授，博士，主要研究方向为电磁理论、复杂系统中的场与波和计算电磁学等。 E-mail: bwei@xidian.edu.cn
李林茜(1985–)，男，博士研究生，主要研究方向为计算电磁学。 E-mail: 395106835@qq.com
通讯联系人, 魏兵 bwei@xidian.edu.cn
摘要：时域离散伽辽金法(Discontinuous Galerkin Time Domain, DGTD)同时具有时域有限元算法(Finite Element Time Domain, FETD)非结构网格剖分和时域有限差分算法(Finite Difference Time Domain, FDTD)显式迭代的优点，是一种非常有前途的电磁计算方法，该文首先描述了基于矢量基函数的时域离散伽辽金法的基本原理。然后，给出了DGTD处理散射问题时平面波入射加入的具体实现方法。最后，给出了金属球、介质球和金属弹头宽带散射的算例，算例结果的比较表明了该文算法的正确性和有效性。该文的研究，为复杂目标雷达散射截面RCS的准确预估打下了坚实的基础。
关键词： 时域离散伽辽金方法    时域有限差分    有限元    雷达散射截面     
Preliminary Research on RCS Using DGTD
Yang Qian①②, Wei Bing①② , Li Lin-qian①②, Ge De-biao①②     
① School of Physics and Optoelectronic Engineering, Xidian University, Xi’an 710071, China
② Collaborative Innovation Center of Information Sensing and Understanding, Xidian University, Xi’an 710071, China
Abstract: Discontinuous Galerkin Time Domain (DGTD) method appears to be very promising which combines the advantages of unstructured mesh in Finite Element Time Domain (FETD) and explicit scheme in Finite Difference Time Domain (FDTD). This paper first describes principle of DGTD base on vector basis function. Secondly, Specific method for incident plane wave is given for scattering problem. At last, the monostatic Radar Cross Section (RCS) of PEC sphere, medium sphere and the PEC bullet are computed by DGTD method. The numerical results illustrate the feasibility and correctness of the presented scheme. The study of this paper is a foundation for analyzing the RCS of complex target.
Key words: Discontinuous Galerkin Time Domain (DGTD)    Finite Difference Time Domain (FDTD)    Finite Element Method (FEM)    Radar Cross Section (RCS)    
1 引言

在目标特性的精确预估中，矩量法(Method of Moment,MoM)、有限元法(Finite Element Method,FEM)和时域有限差分方法(Finite Difference Time Domain,FDTD)均是应用广泛的计算方法。MoM主要长于金属目标散射问题的处理，FEM和FDTD方法则更适宜于复杂媒质的计算。MoM和FEM需要求解大型线性方程组，应用于电大尺寸目标时求解效率低。FDTD采用显式迭代的方式，易于并行计算，并且计算复杂度低，但其在对目标拟合上存在台阶误差，即使采取亚网格或共形网格也很难精确拟合。近年来，离散伽辽金法(Discontinuous Galerkin method)算法受到了人们的重视[1]。该算法在流体力学及有限体积法(Finite volume method)中早有应用[2]，近年来被引入有限元计算当中来形成了时域离散伽辽金算法(Discontinuous Galerkin Time Domain,DGTD)[3, 4]。DGTD结合了FDTD显式迭代和FEM网格精确拟合目标几何性形状的特点，是一种有广阔应用前景的计算方法。近十余年，国际上的同行对该方法已经进行了多方面的研究，但在国内将基于矢量基函数的DGTD方法用于目标散射特性的分析还未见相关报道。本文首先简要介绍了基于棱边矢量基函数的3维DGTD方法的基本思想。然后，给出了在该方法实现中的平面波引入及总场边界条件。最后，给出目标单站散射特性的算例表明本文算法的正确性。

2 基于棱边基函数的3维DGTD

DGTD可以看作由时域有限元方法(Finite Element Time Domain,FETD)改变边界条件的处理方式得到。FETD是从支配方程和边界条件出发将计算区域划分为多个单元后导出矩阵方程并求解的方法，J. M. Jin,J. F. Lee等人在FETD方面做了很多工作[5, 6, 7]。一般来说，FETD方程推导有两种途径，即变分法与Galerkin法。变分法寻找一个适当泛函对应于支配方程和边界条件，Galerkin法通过加权余量来寻找支配方程和边界条件的相应弱解形式。两种方法都会得到一个大型矩阵方程。在FETD中的若干基本概念如基函数、单元积分、局域、全域、Galerkin加权等均可在DGTD中继承使用，而两种有限元算法的局域边界处理方式有差异。

下面从Maxwell方程组出发描述DGTD的基本思想，Maxwell旋度方程为：

$\left. \begin{array}{l} \varepsilon \frac{{\partial E}}{{\partial t}} - \nabla \times H + \sigma E = - J\\ \mu \frac{{\partial E}}{{\partial t}} + \nabla \times E + {\sigma _m}H = - {J_m} \end{array} \right\}$ (1)
式中e为介电系数，m为磁导系数；s为电导率，sm为导磁率；E和H分别为电场强度矢量与磁场强度矢量；J与Jm分别为电磁流。

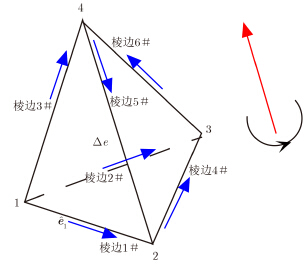
本文中采用四面体作为DGTD算法的基本离散单元(如图 1所示)，采用Galerkin加权法[6]，对式(1)在四面体单元内积分，可得

图 1 四面体单元示意图 Fig.1 Schematic diagram of tetrahedron

$\left. \begin{array}{l} \int {v \cdot } \left[ {\varepsilon \frac{{\partial E}}{{\partial t}} - \nabla \times H + \sigma E + J} \right]d\Omega = 0\\ \int {v \cdot } \left[ {\mu \frac{{\partial E}}{{\partial t}} + \nabla \times E + {\sigma _m}H + {J_m}} \right]d\Omega = 0 \end{array} \right\}$ (2)

式中v为积分权函数。对式(2)中包含$ \nabla \times {H}$及$ \nabla \times {E}$的体积分项做代数变换
$\left. \begin{array}{l} \int {v \! \cdot \! } \left( {\nabla \!\! \times \!\! E} \right)d\Omega \!\! = \!\! \int {\nabla \cdot } \left( {E \!\! \times \!\! v} \right)d\Omega \!\! + \!\! \int {E \cdot } \left( {\nabla \!\! \times \!\! v} \right)d\Omega \!\! = \!\! \int {\mathop n\limits^ \wedge \cdot } \left( {E \!\! \times \!\! v} \right)ds \!\! + \!\! \int {E \cdot } \left( {\nabla \!\! \times \!\! v} \right)d\Omega \\ \!\! \!\! \quad \quad \qquad \qquad \,\,\,\, = \int {v \! \cdot \! } \left( {\mathop n\limits^ \wedge \!\! \times \!\! E} \right)ds \!\! + \!\! \int {E \! \cdot \! } \left( {\nabla \!\! \times \!\! v} \right)d\Omega \\ \!\! \!\! \!\! \!\! \quad \,\,\, \int {v \! \cdot \! } \left( {\nabla \!\! \times \!\! H} \right)d\Omega \!\! = \!\! \int {\nabla \cdot } \left( {H \!\! \times \!\! v} \right)d\Omega \!\! + \!\! \int {H \cdot } \left( {\nabla \!\! \times \!\! v} \right)d\Omega \!\! = \!\! \int {\mathop n\limits^ \wedge \cdot } \left( {H \!\! \times \!\! v} \right)ds \!\! + \!\! \int {H \cdot } \left( {\nabla \!\! \times \!\! v} \right)d\Omega \\ \!\! \!\! \quad \quad \qquad \qquad \,\,\,\, = \!\! \int {v \! \cdot \! } \left( {\mathop n\limits^ \wedge \!\! \times \!\!H} \right)ds \!\! + \!\! \int {H \! \cdot \! } \left( {\nabla \!\! \times \!\! v} \right)d\Omega \!\! \!\! \!\! \!\! \end{array} \right\}$ (3)
式中$ \hat {n}$为积分面上外法向单位矢量。经变换后的式(3)中出现了沿边界(四面体表面)的积分项，计算时需要设定边界条件。

在流体力学中为求解双曲方程，边界条件采用Numerical Flux[2]，后又被引入了时域有限体积法(FVTD)[8]，又被引入DGTD作核心思想[4]。在边界上定义E*与H*为：

$\left. \begin{array}{l} \mathop n\limits^ \wedge \times {E^ * } = \mathop n\limits^ \wedge \times E + K_E^e\left[ {\mathop n\limits^ \wedge \times \left( {{E^ + } - E} \right)} \right]\\ \quad \quad \qquad \,\,\,+ v_H^e\left[ {\mathop n\limits^ \wedge \times \left( {\mathop n\limits^ \wedge \times \left( {{H^ + } - H} \right)} \right)} \right]\\ \mathop n\limits^ \wedge \times {H^ * } = \mathop n\limits^ \wedge \times H + K_H^e\left[ {\mathop n\limits^ \wedge \times \left( {{H^ + } - H} \right)} \right]\\ \quad \quad \qquad \,\,\,- v_E^e\left[ {\mathop n\limits^ \wedge \times \left( {\mathop n\limits^ \wedge \times \left( {{E^ + } - E} \right)} \right)} \right] \end{array} \right\}$ (4)
式(4)中E*与H*称为Numerical Flux，在两个相邻的四面体单元面两侧不相等但依赖于两个相接面的切向场；$ \hat {n}$为外法向单位矢量，E,H为待计算单元场值，E+,H+为与待计算单元的相邻单元场值。$k_{\rm{E}}^e$,
$k_{\rm{H}}^e$,$v_{\rm{H}}^e$,$v_{\rm{E}}^e$的取值如表 1[4]。
表 1 Numerical Flux系数表达式 Tab. 1 Coefficient of Numerical Flux

表 1中${Y^e} = \sqrt {{\varepsilon ^e}/{\mu ^e} = 1/{Z^e}} $,e为当前单元，e+为相邻单元。

由于E*,H*仅定义在边界上，可得

$\left. \begin{array}{l} \int {v \! \cdot \! } \left( {\nabla \!\! \times \!\! {E^ * }} \right)d\Omega \!\! = \!\! \int {v \! \cdot \! } \left( {\nabla \!\! \times \!\! E} \right)d\Omega \!\! + \!\! \int {\left\{ {k_E^e\left[ {\mathop n\limits^ \wedge \times \left( {{E^ + } \!\! - \!\! E} \right)} \right] \!\! + \!\! v_H^e\left[ {\mathop n\limits^ \wedge \times \left( {\mathop n\limits^ \wedge \times \left( {{H^ + }\!\! - \!\! H} \right)} \! \right)} \! \right]} \! \right\}} \! ds \!\! \!\! \\ \int {v \! \cdot \! } \left( {\nabla \!\! \times \!\! {H^ * }} \right)d\Omega \!\! = \!\! \int {v \! \cdot \! } \left( {\nabla \!\! \times \!\! H} \right)d\Omega \!\! + \!\! \int {\left\{ {k_H^e\left[ {\mathop n\limits^ \wedge \times \left( {{H^ + } \!\! - \!\! H} \right)} \right] \!\! + \!\! v_E^e\left[ {\mathop n\limits^ \wedge \times \left( {\mathop n\limits^ \wedge \times \left( {{E^ + } \!\! - \!\! E} \right)} \! \right)} \! \right]} \! \right\}} \! ds \!\! \!\! \end{array} \right\}$ (5)

将式(5)代入式(2)，

$\left. \begin{array}{l} \varepsilon \int {v \cdot } \frac{{\partial E}}{{\partial t}}d\Omega \!\! - \!\! \int {v \! \cdot \! } \left( {\nabla \! \times \! H} \right)d\Omega \!\! - \!\! \int {\left\{ {k_H^e\left[ {\mathop n\limits^ \wedge \!\! \times \!\! \left( {{H^ + } \! - \! H} \right)} \right]ds \!\! + \!\! \int {v_E^e} \left[ {\mathop n\limits^ \wedge \!\! \times \!\! \left( {\mathop n\limits^ \wedge \!\! \times \!\! \left( {{E^ + } \! - \! E} \right)} \! \right)} \! \right]} \! \right\}} \! ds \!\!\! \\ \qquad \qquad \,\,\,\,\, + \sigma \int {v \cdot } Ed\Omega + \int {v \cdot } Jd\Omega = \!\! 0 \!\! \\ \mu \int {v \cdot } \frac{{\partial H}}{{\partial t}}d\Omega \!\! + \!\! \int {v \! \cdot \! } \left( {\nabla \! \times \! E} \right)d\Omega \!\! + \!\! \int {\left\{ {k_E^e\left[ {\mathop n\limits^ \wedge \!\! \times \!\! \left( {{E^ + } \! - \! E} \right)} \right]ds \!\! + \!\! \int {v_H^e} \left[ {\mathop n\limits^ \wedge \!\! \times \!\! \left( {\mathop n\limits^ \wedge \!\! \times \!\! \left( {{H^ + } \! - \! H} \right)} \! \right)} \! \right]} \! \right\}} \! ds \!\!\! \\ \qquad \qquad \,\,\,\,\,\, + {\sigma _m}\int {v \cdot } Hd\Omega + \int {v \cdot } {J_m}d\Omega \!\! = 0 \!\! \end{array} \right\}$ (6)

经整理后得矩阵形式的偏微分方程组，此方程组针对单个四面体，实际计算中在计算域内循环所有四面体迭代求解。

 

$\left. \begin{array}{l} \varepsilon \left[ {{M^e}} \right]\frac{\partial }{{\partial t}}\left\{ {{E^e}} \right\} - \left[ {{S^e}} \right]\left\{ {{H^e}} \right\} - \left\{ {F{h^e}} \right\} + \sigma \left[ {{M^e}} \right]\left\{ {{E^e}} \right\} + \left\{ {{J^e}} \right\} = 0\\ \mu \left[ {{M^e}} \right]\frac{\partial }{{\partial t}}\left\{ {{H^e}} \right\} + \left[ {{S^e}} \right]\left\{ {{E^e}} \right\} + \left\{ {F{e^e}} \right\} + {\sigma _m}\left[ {{M^e}} \right]\left\{ {{H^e}} \right\} + \left\{ {{J^e}_m} \right\} = 0 \end{array} \right\}$ (7)

本文采用Whitney-I型矢量基函数[9]，Me,Se,Fhe,Fee,Je,Jm矩阵元素表达式如下：

$\left. {\begin{array}{*{20}{l}} {M_{ij}^e = \iiint\limits_{{\Omega ^e}} {N_i^e \cdot }N_j^ed\Omega ,S_{ij}^e = \iiint\limits_{{\Omega ^e}} {N_i^e \cdot }(\nabla \times N_j^e)d\Omega } \\ {Fh_i^e = \sum {\left[ {k_H^e} \right]} \cdot \left\{ {H_j^{e + } - H_j^e} \right\} - \sum {\left[ {\nu _E^e} \right]} } \\ {\quad \quad \quad \; \cdot \left\{ {E_j^{e + } - E_j^e} \right\}} \\ {\quad \quad = \sum {k_H^e\left[ {Mf_{ij}^e} \right]} \cdot \left\{ {H_j^{e + } - H_j^e} \right\} - \sum {\nu _E^e\left[ {M{\text{g}}_{ij}^e} \right] \cdot \left\{ {E_j^{e + } - E_j^e} \right\}} } \\ {F{\text{e}}_i^e = \sum {\left[ {k_H^e} \right]} \cdot \left\{ {E_j^{e + } - E_j^e} \right\} + \sum {\left[ {\nu _H^e} \right]} } \\ { \quad \quad \quad \; \cdot \left\{ {H_j^{e + } - H_j^e} \right\}} \\ { \quad \quad = \sum {k_E^e\left[ {Mf_{ij}^e} \right]} \cdot \left\{ {E_j^{e + } - E_j^e} \right\} - \sum {\nu _H^e\left[ {M{\text{g}}_{ij}^e} \right] \cdot \left\{ {H_j^{e + } - H_j^e} \right\}} } \\ { \; \; J_i^e = \iiint\limits_{{\Omega ^e}} {N_i^e \cdot } \cdot J_i^ed\Omega ,J_{mi}^e = \iiint\limits_{{\Omega ^e}} {N_i^e \cdot } \cdot J_m^ed\Omega } \end{array}} \right\}$ (8)

式(8)中的${N}_i^e$,${N_j^e}$为基函数，

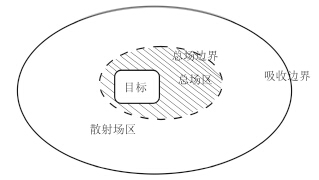
3 DGTD中的平面波引入及总场边界条件

用DGTD计算散射问题时可将计算区域划分为总场区和散射场区，如图 2所示。采用等效原理，类似FDTD中的总场边界条件，在总场边界上设置入射波的切向分量即可将入射波引入到总场区[10]。

图 2 总场区与散射场区的划分 Fig.2 The total field region and the scattered field region

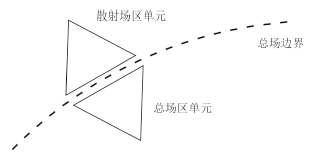
为便于说明总场边界条件的加入，图 3中以三角形代替四面体，规定散射场区单元的场均属于散射场，总场区单元的场均属于总场。在总场区内部及散射场区内部，DGTD计算方式如前文所述，需要特殊处理的是边界处相邻的单元计算式，具体来讲是在Numerical Flux表达式中增加入射波的计算部分。

图 3 DGTD总场散射场边界 Fig.3 TF/SF boundary for DGTD

(1) 当四面体处于总场边界的总场区一侧时，应在Numerical Flux上加上入射波值，此时$E_j^e$,$H_j^e$属于总场，$E_j^{e+}$,$H_j^{e+}$属于散射场，Ei,Hi为入射波。

$ \left. \begin{array}{1} {\rm{Fh}}_j^e = \sum\limits {k_{\rm{H}}^e\left[{{\rm{Mf}}_{ij}^e} \right] \cdot \left\{ {H_j^{e + } - H_j^e + {\rm{Hi}}} \right\}} \\ \quad\quad\quad - \sum\limits {v_{\rm{E}}^e\left[{{\rm{Mg}}_{ij}^e} \right] \cdot \left\{ {E_j^{e + } - E_j^e + {\rm{Ei}}} \right\}} \\ {\rm{Fe}}_j^e = \sum\limits {k_{\rm{E}}^e\left[{{\rm{Mf}}_{ij}^e} \right] \cdot \left\{ {E_j^{e + } - E_j^e + {\rm{Ei}}} \right\}} \\ \quad\quad\quad + \sum\limits {v_{\rm{H}}^e\left[{{\rm{Mg}}_{ij}^e} \right] \cdot \left\{ {H_j^{e + } - H_j^e + {\rm{Hi}}} \right\}} \end{array} \!\!\! \right\}$ (9)

(2) 当四面体处于总场边界的散射场区一侧时，应在Numerical Flux上减去入射波值，此时3$E_j^e$,$H_j^e$属于散射场，$E_j^{e+}$,$H_j^{e+}$属于总场，Ei,Hi为入射波。

$ \left. \begin{array}{l} {\rm{Fh}}_j^e = \sum\limits {k_{\rm{H}}^e\left[{{\rm{Mf}}_{ij}^e} \right] \cdot \left\{ {H_j^{e + } - H_j^e - {\rm{Hi}}} \right\}} \\ \quad\quad\quad - \sum\limits {v_{\rm{E}}^e\left[{{\rm{Mg}}_{ij}^e} \right] \cdot \left\{ {E_j^{e + } - E_j^e - {\rm{Ei}}} \right\}} \\ {\rm{Fe}}_j^e = \sum\limits {k_{\rm{E}}^e\left[{{\rm{Mf}}_{ij}^e} \right] \cdot \left\{ {E_j^{e + } - E_j^e - {\rm{Ei}}} \right\}} \\ \quad\quad\quad + \sum\limits {v_{\rm{H}}^e\left[{{\rm{Mg}}_{ij}^e} \right] \cdot \left\{ {H_j^{e + } - H_j^e - {\rm{Hi}}} \right\}} \end{array} \!\!\! \right\}$ (10)

采取上面的方法即可将平面波引入总场区域。

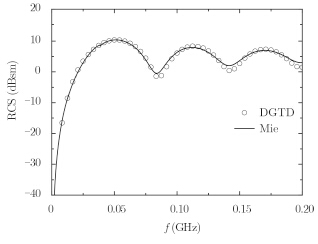
4 算例

为说明本文算法的正确性，用DGTD方法计算半径为1 m的金属球的后向RCS并与解析解结果相对比。计算区域被离散成为319308个四面体(计算域剖分截面图如图 4所示)，空间离散尺度为0.15 m，采用1阶Mur吸收边界。图 5是金属球后向单站RCS的计算结果(圆圈)，作为比较，图中还给出了Mie级数计算结果(实线)，由图可见两者的结果吻合较好。本算例DGTD消耗内存约280 MB，计算耗时约20 min，计算平台为Intel Core i5 3470；采用FETD计算所需内存消耗为2 G，计算时间在6 h以上。显然，本文方法有更高的计算效率。

图 4 计算域剖分截面图 Fig.4 Sectional view of the computational domain

图 5 金属球单站RCS Fig.5 The monostatic RCS of PEC sphere

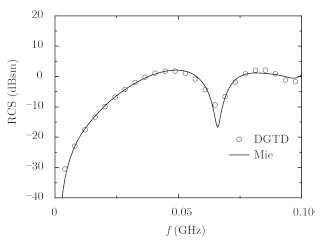
设介质球参数为e=4e0,m=m0,s=0.00015 S/m，其余参数同上。图 6是本文方法(圆圈)与Mie级数计算结果(实线)的比较，由图可见，两者相吻合。

图 6 介质球单站RCS Fig.6 The monostatic RCS of medium sphere

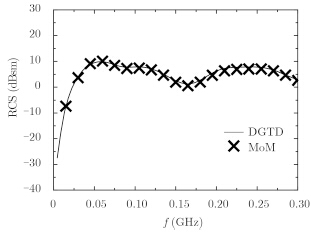
为说明本文算法对于计算较为复杂目标的适用性，下面计算金属弹头的后向RCS。弹头模型如图 7所示(底面半径为1 m，高为2 m)。电磁波沿z轴负方向，电场沿x方向极化入射。图 8为弹头的后向RCS，实线为DGTD算法的结果，斜十字为MoM算法扫频结果。由图可见，两种算法的结果符合较好。

图 7 弹头模型 Fig.7 Model of PEC bullet

图 8 金属弹头单站RCS Fig.8 The monostatic RCS of PEC bullet
5 结论

在散射问题的DGTD的分析中吸收边界条件、时间离散方式、近远场外推和四面体相邻单元的快速判断等方面都需要精细考虑，限于篇幅，本文没有讨论这些内容。目前，由于吸收边界采用1阶Mur吸收边界，本文算例中DGTD的计算精度有待提高。采用UPML吸收边界、高阶基函数及精度更高的时间离散方案将是我们下一步的工作。可以预期，作为一种新兴算法，DGTD将在目标特性的精确预估，特别是含复杂媒质的低RCS目标特性的精确预估方面扮演重要角色。

参考文献
[1] Ji X, Lu T, Cai W, et al.. Discontinuous Galerkin Time Domain (DGTD) methods for the study of 2-D waveguidecoupled microring resonators[J]. Journal of Lightwave Technology, 2005, 23(11): 3864-3874.(1)
[2] Shu C W. A brief survey on discontinuous Galerkin methods in computational fluid dynamics[J]. Advances in Mechanics, 2013, 43(6): 541-553.(1)
[3] Gedney S D, Kramer T, Luo C, et al.. The Discontinuous Galerkin Finite Element Time Domainmethod(DGFETD)[C]. IEEE International Symposium on Electromagnetic Compatibility, 2008: 1-4.(1)
[4] Alvarez J. A Discontinuous Galerkin Finite Element Method for the Time-Domain Solution of Maxwell Equations[D]. [Ph.D. dissertation], University of Granada (Spain), 2013: 31-39.(3)
[5] Lee Jin-Fa, Lee Robert, and Cangellaris Andreas. Timedomain finite-element methods[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(3): 430-442.(1)
[6] Jin Jian-ming.The Finite Element Method in Electromagnetic[M]. New York: John Wiley & Sons, 2002: 22-23.(2)
[7] Riley D J, Jin Jian-ming, Lou Z, et al.. Total-and scatteredfield decomposition technique for the finite-element timedomain method[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(1): 35-41.(1)
[8] Shankar V, Mohammadian A H, and Hall W F. A timedomain, finite-volume treatment for the Maxwell equations[J]. Electromagnetics, 1990, 10(1/2): 127-145.(1)
[9] Bossavit A. Whitney forms: a class of finite elements for three-dimensional computations in electromagnetism[J]. IEE Proceedings A (Physical Science, Measurement and Instrumentation, Management and Education, Reviews), 1988, 135(8): 493-500.(1)
[10] 葛德彪, 魏兵. 电磁波时域计算方法(下册)[M]. 西安电子科技 大学出版社, 2014: 188-191. Ge D B and Wei B. Time Domain Computational Method for Electromagnetic Wave (Volume II)[M]. Xi'an: Xidian University Press, 2014: 188-191.(1)