② 中国传媒大学信息工程学院 北京 100024
② Information Engineering School, Communication University of China, Beijing 100024, China
按照是否考虑电磁散射过程,SAR仿真方法可以分为图像级和信号级两类方法[1]。图像级仿真方法仅模拟SAR图像的特征,不考虑场景中目标与环境的电磁散射过程,利用现有的或假设的散射系数图(如光学或SAR图像)来模拟SAR数据;信号级仿真方法则关注电磁散射过程,通过对复杂地物场景和SAR平台运动的建模,结合计算电磁学方法模拟SAR回波数据。从本质上讲,SAR图像级仿真只是基于点散射源的简单电磁散射模型,相对而言,SAR信号级仿真则能更加真实地模拟SAR探测过程中电磁波与场景中目标与环境的作用机理。随着定量遥感、目标检测和目标识别等技术的发展,SAR信号级仿真已成为国内外研究的热点[2, 3, 4, 5]。
基于计算电磁学方法实现对地面车辆目标高质量SAR模板图像快速仿真,是一个极具技术挑战性的物理和数学问题。在解决这一问题的过程中,不但需要采用解析或统计描述,建立对地面粗糙特性的准确表达,而且必须发展适合于地面与目标间的复合电磁散射计算的方法。传统的采用均方根高度和相关长度等统计信息来简单地表征地面,无法反映出地面总体的起伏特性和自身的纹理结构,且仅对较为平坦的地面有效[6];常见的地面电磁散射模型[7, 8]虽然精度较高,但往往都存在一定的推导假设和适用范围,并且模型的时间和空间复杂度通常较高;在地面目标复合散射特性建模方面,Johnson利用四路径模型计算了无限大介质平板上方的介质目标的散射[9];Franceschetti[10, 11]基于Kirchhoff近似提出一种模拟地面散射特性的小面元模型,并基于该模型实现了对复杂地面场景的SAR图像仿真,但小面元模型无法考虑地面间的多次耦合散射贡献,并且为了更好地描述地表的随机起伏,面元的尺寸必须足够小,致使其对大规模地面场景散射特性仿真的效率较低;Didascalou[12]提出的基于切平面近似的随机散射法(SSA)结合射线投射的思想实现了对微粗糙、中等粗糙和高粗糙面相干和非相干分量的快速计算,但亦无法计算粗糙面不同部分间的耦合散射贡献;Kulpa等[13]提出几何光学法(GO)和时域有限差分法(FDTD)混合方法,实现对复杂地面场景SAR回波的快速仿真,但未对模型的有效性进行充分验证。国内,计科峰等人[14]利用高频法实现了坦克目标的SAR图像仿真;张锐等人[15]运用弹射线原理,通过仿真不同位置、不同频点的目标后向散射系数来构建回波并成像;郭立新等人[16]引入互易性定理结合高频算法给出了粗糙面与其上方球形目标和平板目标的复合电磁散射计算方法。目前,这些电磁计算方法尚缺乏与实际测量结果比较,同时计算内存和时间消耗较大,难以满足复杂目标海量高质量SAR模板仿真等工程应用的需求。
为了实现对地面车辆目标高质量SAR模板图像的快速仿真,本文提出一种基于射线追踪技术的SAR信号级快速仿真方法。该方法首先通过建立地面车辆目标SAR仿真场景物理模型,并利用射线追踪方法精确获取雷达与目标/环境的空间几何关系;然后,基于随机散射法原理并结合地杂波统计模型实现对地面的粗糙特性的高效模拟;再次,基于射线管分裂方法建立表面粗糙的复杂目标宽带电磁散射模型,获取复杂目标的镜面反射、边缘绕射和多次反射贡献;最后基于射线追踪方法建立地面场景宽带耦合电磁散射模型,准确计算目标-环境间的耦合散射贡献。基于上述仿真场景模型和电磁散射模型计算地面车辆目标的扫频数据,并通过时频变换和成像处理得到车辆目标的SAR图像,经过相似度评估确认形成高质量SAR模板图像。
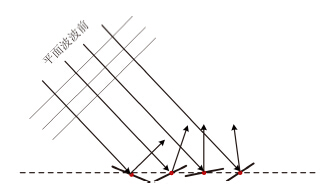
2 随机散射方法原理随机散射方法的原理如图 1所示,其本质是一种蒙特卡罗(Monte Carlo)方法,能够较真实地模拟射线在微粗糙、中等粗糙甚至高粗糙表面上镜面反射和漫反射现象。
|
图 1 随机散射方法的原理示意图 Fig.1 Principle of stochastic scattering approach |
随机粗糙方法[12]首先假定粗糙面的局部的起伏高度h为(或近似为)均值为0、标准差为sh的Gauss随机数,即
| ${p_{\rm{h}}}(h) = {1 \over {\sqrt {2\pi } {\sigma _{\rm{h}}}}}\exp \left[ { - {1 \over 2}{{\left( {{h \over {{\sigma _{\rm{h}}}}}} \right)}^2}} \right]$ | (1) |
| ${\phi _{{\rm{hh}}}}\left( l \right) = \exp \left( { - \frac{{{l^2}}}{{{L^2}}}} \right)$ | (2) |
| $\left\langle {h{_x^{\prime2}} + h{_y^{\prime2}}} \right\rangle = \frac{{2{\sigma _{\rm{h}}}}}{L}$ | (3) |
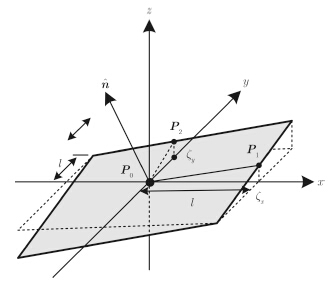
随机散射方法设定的粗糙面局部切平面如图 2所示。该平面由P0(0,0,0),P1(L/${\sqrt 2 }$,0,zx)和 P2 (0,L/${\sqrt 2 }$,zy)确定,其法向${\hat n}$表示为:
| ${{\hat n}} = \frac{{\left( { - {{\sqrt 2 {\zeta _x}} \mathord{\left/{\vphantom {{\sqrt 2 {\zeta _x}} L}} \right.} L},- {{\sqrt 2 {\zeta _y}} \mathord{\left/{\vphantom {{\sqrt 2 {\zeta _y}} {L,1}}} \right.} {L,1}}} \right)}}{{\left\| {\left( { - {{\sqrt 2 {\zeta _x}} \mathord{\left/{\vphantom {{\sqrt 2 {\zeta _x}} L}} \right.} L},- {{\sqrt 2 {\zeta _y}} \mathord{\left/{\vphantom {{\sqrt 2 {\zeta _y}} {L,1}}} \right.} {L,1}}} \right)} \right\|}}$ | (4) |
|
图 2 粗糙面局部切平面示意图 Fig.2 Local tangent plane of rough surface |
因此,为了能够获得仿真场景中各采样点处的切平面,随机散射方法仅需额外产生zx,zy和采样点处的起伏高度hz 3个相互独立的均值为0,标准差为sh的Gauss分布的随机数。由于采用了切平面近似,随机散射方法须要满足下面的适用条件:
| $\frac{{{L^2}}}{{2.76{\sigma _{\rm{h}}}}} > \lambda,\quad L > \frac{6}{2 π} \lambda $ | (5) |
与小面元模型相似,随机散射方法同样基于切平面近似,亦无法考虑环境面元间的多次耦合散射贡献,但该方法结合射线投射思想实现了对随机粗糙面相干和非相干分量的同步模拟。
3 目标-地面复合散射特性建模 3.1 SAR仿真场景物理模型为构建适用于电磁散射计算的地面场景的物理模型,需要完成对场景中各物理要素的合理科学配置。主要包括3个步骤:
第1步 地面环境覆盖类型和属性参数设定。
针对SAR回波仿真工程应用需求,结合Ulaby地物分类方法,首先按表 1对实际地面场景中的地物类型进行分类。
| 表 1 典型地物类型分类及属性参数 Tab. 1 Categorization and property parameter of typical terrains |
其次,按地物类型的不同将地面场景的非均匀网格模型划分为不同的部件,每一个部件归集一类地物,或属性参数不同的同一类地物(如草地中的高草地和矮草地、森林中的夏日森林和冬日森林,或者雪地中的干雪地和湿雪地等)。
最后,分部件设定各部件的地物类型和属性参数。对于山地、灌木和道路等基本类型地物,可仅设置其地物类型;对于草地、森林和雪地等复杂类型地物,除需要设置其地物类型外,还需进一步明确其属性参数,如草高、季节和干湿等等。
第2步 目标表面材料和粗糙度参数设置。由于复杂目标,尤其是飞机和车辆,各部件在研制过程的工艺精度通常不同,如飞机机翼通常会被铣磨得十分光滑以减小行进时空气阻力,而通过铸造等粗加工成型部件如坦克、装甲等的表面则相对粗糙。为了实现对复杂目标的电磁散射特性的准确仿真,必须首先实现对目标表面粗糙度定量的描述。
根据粗糙面散射理论[8],并依据工程实际情况,对复杂目标表面的粗糙程度进行分级处理,具体分级参数如表 2所示。表中,$\hat \sigma $为粗糙面高度起伏均方根,$\hat \theta $为平均法向偏角;l0为入射波波长。表面粗糙程度中,一级和二级粗糙适用于描述铣磨等精加工工艺处理得到的光滑或微粗糙表面,如船舷外面等;三级和四级粗糙则适用于描述铸造等粗加工处理的目标表面粗糙,如坦克、装甲等。
| 表 2 表面粗糙程度分级参数 Tab. 2 Grading parameters of surface roughness |
第3步 目标在场景的姿态位置自适应调整。在将目标引入到实际地面环境中时,需要进行目标-环境的适应性装配处理以确保目标位于地面上且目标的姿态适应于环境表面总体起伏。另外,还可以根据需要调节目标方位姿态,使其朝向给定方位。为了更直观地理解目标-环境的适应性装配,图 3给出了将坦克目标配置到地面场景的道路上的适应性装配和姿态调整过程示意图。

|
图 3 坦克与道路姿态位置自适应调整过程示意图 Fig.3 Adjustment procedures of introducing tank onto road surface |
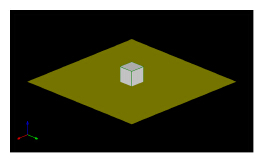
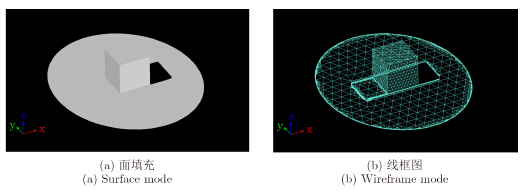
图 4给出按上述方法构建的90 m×90 m地面上置边长10 m立方体场景物理模型的效果图,三角网格尺寸为1 m。图 5为采用文献[17]方法消隐重构的该场景在聚束SAR航迹中心点处的物理模型,三角网格最小尺寸为0.1 m。可以看出,消隐重构的仿真场景模型实现了对SAR探测波束照亮范围、目标-环境耦合区域以及阴影区域的准确识别,并且消隐过程中的射线管分裂结果可直接用于电磁散射特性计算,将显著提高SAR模板图像的仿真效率。
|
图 4 地面上立方体SAR仿真物理模型图 Fig.4 Physical model of the ground cube for SAR simulation |
|
图 5 消隐重构的立方体SAR仿真物理模型图 Fig.5 Physical model of the cube scene after hidden-surface-removal procedure |
本节利用改进的射线弹跳法和等效边缘流法快速预估目标粗糙表面的镜面反射、多次反射以及细分边缘的绕射3种高频散射主要贡献,建立表面粗糙的复杂目标宽带电磁散射模型。具体步骤如下:
第1步 基于消隐处理中构建的细分子射线管,采用口面积分法计算各子射线管的多次反射场,通过相干叠加获得目标多次反射贡献。
为了模拟目标表面随机起伏特性对目标表面散射特性的影响,在射线追踪到的各个反射点Pj处做如下修正:
(1) 沿原反射面法向${{{\hat n}}_\rm{i}}$引入高程差DHj,修正反射点Pj 到${P_j}^\prime$点
| ${{P_j}^\prime = P_j} + \Delta {H_j} \cdot {{{\hat n}}_\rm{i}}$ | (6) |
(2) 对原反射面法向${{{\hat n}}_\rm{i}}$引入偏转角Dqi,修正到${\hat n_{\rm{i}}^ \prime}$方向。在反射面局部坐标系下,${{\hat n}}_{\rm{i}}^ \prime $可表示为:
| $ {{\hat n}}_{\rm{i}}^ \prime = \frac{{{{{{\hat n}}}_{\rm{i}}}\cos \left( {\Delta {\theta _{\rm{i}}}} \right) + {{\hat x}_{\rm{c}}}\cos z _j + {{{{\hat y}_{\rm{c}}}\sin z _j}} }} {{\left\| {{{{{\hat n}}}_{\rm{i}}}\cos \left( {\Delta {\theta _{\rm{i}}}} \right) + {{\hat x}_{\rm{c}}}\cos z _j + {{\hat y}_{\rm{c}}}\sin z _j} \right\|}}$ | (7) |
式中,Dqi为服从均匀分布的相干随机数,且Dqi~U[0,${\hat \theta _{\rm{m}}}$],${\hat \theta _{\rm{m}}}$按反射面所在部件的粗糙等级不同分别取表 2中${\hat \theta }$的最大值;zj为服从均匀分布的相干随机数,且zj ~U[0,2p]。目标粗糙表面局部坐标系如图 6所示,具体定义如下:

|
图 6 目标粗糙表面局部坐标系示意图 Fig.6 Local coordinate system of target with rough surfaces |
| $\left. \begin{array}{l} {\hat z_\rm{c}} = {{{{\hat n}}}_\rm{i}}\\ {\hat y_\rm{c}} = {{\left( {{\hat z_\rm{c}} \times {\hat x_\rm{g}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\hat z_\rm{c}} \times {\hat x_\rm{g}}} \right)} {\left\| {{\hat z_\rm{c}} \times {\hat x_\rm{g}}} \right\|}}} \right. } {\left\| {{\hat z_\rm{c}} \times {\hat x_\rm{g}}} \right\|}}\\ {\hat x_\rm{c}} = {\hat y_\rm{c}} \times {\hat z_\rm{c}} \end{array} \right\}$ | (8) |
大量仿真实验表明,引入上述对射线反射点的高程修正和反射面法向的随机偏转能够较好地模拟由目标表面粗糙引起的漫反射效应。
第2步 基于重构的可见三角网格模型识别目标区自然边缘,并利用等效边缘流法计算复杂目标的边缘绕射贡献。为了模拟目标表面随机起伏特性对边缘绕射特性的影响,对识别出的各个自然边缘Ej做如下处理:
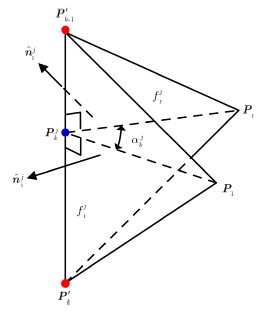
(1) 按lp≈0.2l0对边缘Ej (${P\!_j \!\! \ \! ^1}$,${P\!_j \!\! \ \! ^2}$)进行离散,生成如图 7所示的细分边缘$E_j^k\left( {P_{k - 1}^\prime,P_k^\prime} \right)$。细分边缘总数
|
图 7 目标细分边缘结构示意图 Fig.7 Subdivided edge structure of complex target |
| $M = \left\lceil {{{\left\| {P\!_j \!\! \ \! ^1 - P\!_j \!\! \ \! ^2} \right\|} \mathord{\left/ {\vphantom {{\left\| {P_j^1 - P_j^2} \right\|} {{l_\rm{p}}}}} \right. } {{l_\rm{p}}}}} \right\rceil $ | (9) |
| $P_k^j = \frac{{P_{k - 1}^\prime + P_k^\prime}}{2}$ | (10) |
(2) 按式(7)修正细分边缘$E_j^k$在$P_j^k$处的面元法向${{\hat n}}_j^{\rm{l}}$和${{\hat n}}_j^{\rm{r}}$分别到$\hat n_j^{{{\rm{l}}^\prime }}$和$\hat n_j^{{{\rm{r}}^\prime }} $,则细分边缘的单位矢量方向修正为:
| $\hat e_j^\prime = {{\hat n_j^{{{\rm{l}}^\prime }} \times \hat n_j^{{{\rm{r}}^\prime }}} \over {\left\| {\hat n_j^{{{\rm{l}}^\prime }} \times \hat n_j^{{{\rm{r}}^\prime }}} \right\|}}$ | (11) |
相应地,细分边缘内角修正为:
| $\alpha _k^\prime = {\rm{ }}\pi - {\rm{acos}}\left( {\hat n_j^{{{\rm{l}}^\prime }} \cdot \hat n_j^{{{\rm{r}}^\prime }}} \right)$ | (12) |
第3步 将上两步得到粗糙表面的镜面反射场、多次反射场以及细分边缘绕射场相干叠加,获得准确的复杂目标电磁散射数据。
3.3 地面环境的宽带电磁散射模型为提高地面杂波仿真效率,借鉴随机散射方法思想并结合粗糙面散射的统计模型,实现对大规模地面场景宽带相干杂波的快速仿真。
美国天线实验室的Ulaby和密执安大学的Dobson提出一种适用于平稳区和接近垂直入射区的模型(后简称ULABY模型)[18]:
| ${\sigma ^0}\left( {{\theta _{\rm{i}}}} \right) = {P_1} \! + \! {P_2}\exp \left( { - {P_3} \cdot {\theta _{\rm{i}}}} \right) \! + \! {P_4}\cos \left( {{P_5} \cdot {\theta _{\rm{i}}} \! + \! {P_6}} \right)$ | (13) |
| $\rm{SD}\left( {{\theta _{\rm{i}}}} \right) = {M_1} + {M_2}\exp \left( { - {M_3} \cdot {\theta _{\rm{i}}}} \right)\hspace{90pt}$ | (14) |
与仅能考虑雷达波与环境表面一次作用的随机散射方法不同,本文提出的射线追踪方法能计算地面的一次反射和多次反射贡献。
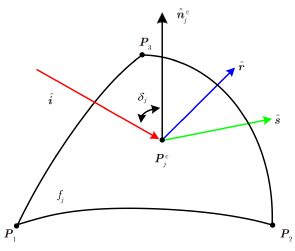
射线追踪方法的原理如图 8所示,该方法在进行地面反射路径的追踪过程中,根据地面局域的粗糙参数产生采样点位置矢量$P\!_j\!\! \ \!^c$
|
图 8 射线追踪方法的原理示意图 Fig.8 Principle diagram of the proposed ray-tracing method |
| $P\!_j\!\! \ \!^c = \left( {u \cdot {P_1} + v \cdot {P_2} + w \cdot {P_3}} \right) + \Delta {H_j} \cdot {{\hat n}}_j^{\rm{c}}$ | (15) |
采样点$P_j^{\rm{c}}$处的法向量${{\hat n}}_j^{\rm{c}}$可通过线性拟合的方法得
| ${{\hat n}}_j^{\rm{c}} = \frac{{u \cdot {{{{\hat n}}}_1} + v \cdot {{{{\hat n}}}_2} + w \cdot {{{{\hat n}}}_3}}}{{\left\| {u \cdot {{{{\hat n}}}_1} + v \cdot {{{{\hat n}}}_2} + w \cdot {{{{\hat n}}}_3}} \right\|}}$ | (16) |
| ${\delta _j} = {\rm{acos}}( - {\hat i} \cdot {{\hat n}}_j^{\rm{c}})$ | (17) |
采用ULABY模型并结合统计分布规律获得局部入射角下$P_j^{\rm{c}}$点处的后向散射贡献
| $E_j^{\rm{c}} = {1 \over 2}\sqrt {{{{A_j}\sigma _j^0} \over \pi }}$ | (18) |
| $E_{\rm{t}}^{\rm{c}}\left( f \right) = n_{\rm{t}}^{\rm{c}} \cdot \sum\limits_{k = 1}^{{N_j}} {\left\{ {E_j^{\rm{c}}\left( f \right)\exp \left[{ - \phi _j^{\rm{c}}\left( f \right)} \right]} \right\}} $ | (19) |
为了提高射线追踪技术计算目标-环境耦合散射的效率,采用与四路径方法相似的策略,只考虑射线与环境发生一次作用的耦合路径上的散射贡献。分两种情况考虑:
(1) 目标→环境路径耦合散射:首先,计算射线在目标表面的镜面/多次反射方向
| ${\hat r\!_j} = {\hat i} - 2\left( {\hat i \cdot {{\hat n}}_j^\prime} \right){{\hat n}}_j^\prime$ | (20) |
(2) 环境→目标路径耦合散射:利用式(16)和式(17)获得的射线在地面采样点$P_j^{\rm{c}}$处的$\left( {\hat n_j^{\rm{c}},{\delta_j}} \right)$,计算射线在环境表面的反射方向
| ${\hat r_j} = \hat i + 2\cos {\delta _j} \cdot {{\hat n}}_j^{\rm{c}}$ | (21) |
最后,总的耦合散射贡献可表达为:
| $E_{\rm{s}}^{\rm{c}}\left( f \right) = \sum\limits_{j = 1}^{{N_{{\rm{tr}}}}} {E_{\rm{s}}^{{\rm{tr}}}\left( f \right)} + \sum\limits_{k = 1}^{{N_{{\rm{cr}}}}} {E_{\rm{s}}^{{\rm{cr}}}\left( f \right)} $ | (22) |
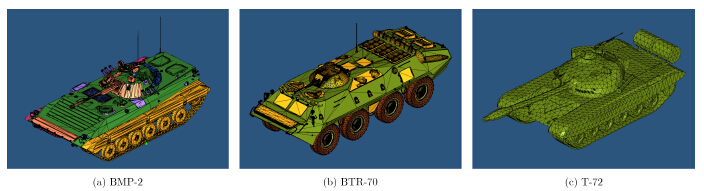
图 9为三型车辆目标的几何模型图。为便于比较,参照MSTAR数据[19]机载SAR测量参数设计表 3所示的SAR仿真参数。仿真中,设定地面环境为矮草地,由ULABY模型确定其在X波段的后向散射系数均值为-28.90 dB,方差为2.95 dB。
|
图 9 车辆目标的几何模型效果图 Fig.9 Geometric models of ground vehicles |
| 表 3 车辆目标聚束SAR仿真参数 Tab. 3 Spotlight SAR parameter for ground vehicle simulation |
基于本文电磁散射建模方法仿真获取草地上三型车辆目标在HH极化下的各轨迹采样点处的宽带复合散射数据,并采用R-D算法直接对宽带数据进行成像处理得到0.2 m像素间隔的SAR仿真图像,如图 10所示。每组图像中前10幅图像的方位角范围为[0,90°],间隔为10°;第11幅图的方位角为135°,第12幅图的方位角为180°。

|
图 10 草地上车辆目标SAR图像仿真结果 Fig.10 Simulated SAR images of ground vehicles on grassland |
从图 10可以看出,由于考虑了目标的散射、环境的散射、目标-环境的耦合散射以及遮挡效应,SAR图像中呈现明显的目标、环境和阴影区域,亮暗对比关系与目标-环境的复合散射机理一致;从表 4到表 6典型方位角下的仿真图像与MSTAR实测图像对比结果可以看出,仿真图像的视觉效果逼真,较为成功。另外,在Core i7 4770 k,NVIDIA GTX780单机上,车辆目标每幅SAR图像的仿真时间约为20 min,峰值内存需求约700 MB;单个车辆目标全方位360幅(方位间隔1°)的SAR模板图集仿真任务能够在5天内完成,基本满足实际工程应用对SAR模板图像仿真效率的需求。
| 表 4 BMP-2的SAR仿真图像与MSTAR实测SAR图像 Tab. 4 Comparison of BMP-2 simulated SAR images with MSTAR measurement images |
| 表 5 BTR-70的SAR仿真图像与MSTAR实测SAR图像 Tab. 5 Comparison of BTR-70 simulated SAR images with MSTAR measurement images |
| 表 6 T-72的SAR仿真图像与MSTAR实测SAR图像 Tab. 6 Comparison of T-72 simulated SAR images with MSTAR measurement images |
进一步,为量化研究仿真结果与MSTAR数据的相似程度,定义仿真图像和实测图像的特征向量f 和g之间的相似度为[20]:
| $C\left( {f,g} \right) = \frac{{{f^{\rm{T}}}g}}{{{{\left\| f \right\|}_2}{{\left\| g \right\|}_2}}}$ | (23) |
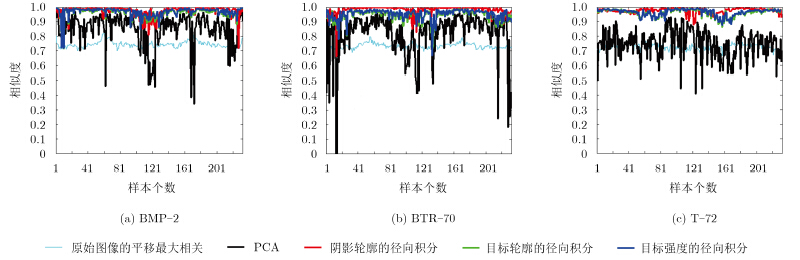
从BMP-2,BTR-70和T-72仿真SAR模板图集中提取与MSTAR数据(子类名称为SN_9563,SN_C71和SN_132,17°擦地角下的图像切片)最邻近方位角上的233,233和232个相应的图像进行相似度评估。图 11给出了文献[14]的平移最大相关系数、文献[15]的PCA和文献[20]径向积分特征的相似度评估结果,相似度均值统计结果如表 7所示。
|
图 11 三型车辆目标仿真与MSTAR实测图像相似度结果 Fig.11 SAR image similarity evaluated results of the ground vehicles |
| 表 7 不同方法下车辆目标仿真与实测图像的相似度均值 Tab. 7 Mean values of image similarities with different methods |
对比分析可知,不同方法下车辆目标仿真与实测图像的相似度均值在70%以上,亦说明仿真较为成功;基于特征的相似度均值在90%以上,表明绝大多数的仿真图像的散射强点分布、散射强点区域轮廓以及阴影轮廓等几何特征均与实测图像高度吻合,验证了本文方法可以获取车辆目标的高质量SAR图像。另外,与T-72相比,BMP-2和BTR-70在头向、侧向和尾向附近方位角下仿真与测量图像相似度相对较低,这主要是BMP-2和BTR-70在这些角度的散射特性与目标表面复杂细节结构密切相关,而仿真中采用的两型目标的几何模型对这些细节的描述不足所致。下一步,将构建更为精细的车辆目标的几何模型,进一步提高电磁散射特性仿真精度和效率,扩展目标-地面复合电磁散射模型的适应范围,实现对各类复杂车辆目标SAR图像的实时/准时精确仿真。
5 结论本文提出的基于射线追踪技术的SAR信号级快速仿真方法通过对地面复杂车辆目标-环境的复合散射特性以及SAR图像几何特征的快速准确模拟,实现了对地面车辆目标高质量SAR模板图像快速仿真。经实测数据校验评估后,基于本文方法仿真获取的地面车辆、机场飞机等目标的SAR模板图像库可为地面目标的识别研究和系统研制提供基础支撑。
致谢 特别感谢厦门大学近海海洋环境科学国家重点实验室的耿旭朴博士在论文SAR回波仿真和成像处理研究中给予作者的帮助。另外,感兴趣的读者可通过邮件索取论文全部角度的仿真图像。| [1] | 保铮, 邢孟道, 王彤编著. 雷达成像技术[M]. 北京: 电子工业出 版社, 2005: 273-293.
( 1) 1) |
| [2] | Cliver C, Quegan S 著; 丁赤飚, 陈杰, 何国金, 等译. 合成孔 径雷达图像理解[M]. 北京: 电子工业出版社, 2009: 79-100.
( 1) 1) |
| [3] | 吴良斌. SAR图像处理与目标识别[M]. 北京: 航空工业出版 社, 2013: 170-230.
( 1) 1) |
| [4] | 李震, 廖静娟. 合成孔径雷达地表参数反演模型与方法[M]. 北 京: 科学出版社, 2011: 170-177.
( 2) 2) |
| [5] | 祝明波, 杨立波, 杨汝良. 弹载合成孔径雷达制导及其关键技 术[M]. 北京: 国防工业出版社, 2014: 148-180.
( 1) 1) |
| [6] | 许小剑, 李晓飞, 刁桂杰, 等. 时变海面雷达目标散射现象学模 型[M]. 北京: 国防工业出版社, 2013: 1-2.
( 1) 1) |
| [7] | Long M W 著, 陈春林, 顾昌贤译. 陆地和海洋的雷达反射特 性[M]. 北京: 国防工业出版社, 1983: 77-89.
( 1) 1) |
| [8] | Ulaby F T, Moore R K, Fung A K 著, 黄培康, 汪一飞译. 微 波遥感(第2卷), 北京: 科学出版社, 1987: 241-250.
( 2) 2) |
| [9] | Johnson J T. A study of the four-path model for scattering from an object above a half space[J]. Microwave and Optical Techniques Letters, 2001, 30(2): 130-134.
( 1) 1) |
| [10] | Franceschetti G, Migliaccio M, Riccio D, et al.. SARAS: a synthetic aperture radar (SAR) raw signal simulator[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(1): 110-123.
( 1) 1) |
| [11] | Franceschetti G, Migliaccio M, and Riccio D. SAR raw signal simulation of actual ground sites described in terms of sparse input data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(6): 1160-1168.
( 1) 1) |
| [12] | Didascalou D. An approach to include stochastic rough surface scattering into deterministic ray-optical wave propagation modeling[J]. IEEE Transactions on Antennas and Propagation, 2003, 51(7): 1508-1515.
( 2) 2) |
| [13] | Kulpa K S, Gromek A, and Salski B.( 1) 1) |
| [14] | An advanced SAR simulator of three-dimensional structures combining geometrical optics and full-wave electromagnetic methods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 776-784. 计科峰, 张爱兵, 邹焕新, 等. 典型地面车辆目标SAR图像仿真 与评估[J]. 雷达科学与技术, 2010, 8(3): 223-228. Ji Ke-feng, Zhang Ai-bing, Zou Huan-xin, et al.. Simulation and evaluation of SAR imagery of typical ground vehicles[J]. Radar Science and Technology, 2010, 8(3): 223-228. (  2) 2) |
| [15] | 张锐, 洪峻, 明峰. 基于电磁散射的复杂目标SAR回波与图像 仿真[J]. 电子与信息学报, 2010, 32(12): 2836-2841. Zhang Rui, Hong Jun, and Ming Feng. SAR echo and image simulation of complex targets based on electromagnetic scattering[J]. Journal of Electronics & Information Technology, 2010, 32(12): 2836-2841. (  2) 2) |
| [16] | 郭立新, 张民, 吴振森. 随机粗糙面与目标复合电磁散射的基 本理论和方法[M]. 北京: 科学出版社, 2014: 228-278.
( 1) 1) |
| [17] | 董纯柱, 殷红成, 王超. 基于射线管分裂方法的SAR场景快速 消隐技术[J]. 雷达学报, 2012, 1(4): 436-440. Dong Chun-zhu, Yin Hong-cheng, and Wang Chao. A fast hidden surface removal approach for complex SAR scene based on adaptive ray-tube splitting method[J]. Journal of Radars, 2012, 1(4): 436-440. (  1) 1) |
| [18] | Ulaby F T and Dobson M C. Handbook of Radar Scattering Statistics for Terrain[M]. Artech House, 1989: 119-357.
( 1) 1) |
| [19] | MSTAR-dataset website. https://www.sdms.afrl.af.mil/ datasets/mstar, 2008. 6.
( 1) 1) |
| [20] | 胡利平, 董纯柱, 邢笑宇, 等. SAR图像目标和阴影径向积分特 征评估[J]. 电波科学学报, 2014, 29(2): 254-259. Hu Li-ping, Dong Chun-zhu, Xing Xiao-yu, et al.. An evaluation method of SAR images based on radial integral features of target and shadow[J]. Chinese Journal of Radio Science, 2014, 29(2): 254-259. (  2) 2) |