二维线性与非线性海面的宽带散射特性仿真及分析

引用本文 [复制中英文]

王佳宁, 许小剑. 二维线性与非线性海面的宽带散射特性仿真及分析[J]. 雷达学报, 2015, 4(3): 343-350. DOI: 10.12000/JR15053.

Wang Jia-ning and Xu Xiao-jian. Simulation and analysis for wide-band scattering characteristics of 2-D linear and nonlinear sea surfaces[J]. Journal of Radars, 2015, 4(3): 343-350. DOI: 10.12000/JR15053.

[复制英文]

基金项目

国家部委基金资助课题

通信作者

许小剑 xiaojianxu@buaa.edu.cn

作者简介

王佳宁(1988–)，女，籍贯甘肃会宁，现为北京航空航天大学电子信息工程学院博士研究生。主要研究方向为海面电磁散射特性仿真及分析。E-mail: manjiaqw@126.com
许小剑(1963–)，男，籍贯江西万安，博士，现为北京航空航天大学电子信息工程学院信号与信息处理学科责任教授，博士生导师。主要研究方向为遥感特征建模、分析与处理、雷达成像与目标识别、智能化信息处理等。E-mail: xiaojianxu@buaa.edu.cn

文章历史

收稿：2015-05-05
改回：2015-06-23

Contents Abstract Full text Figures/Tables PDF

二维线性与非线性海面的宽带散射特性仿真及分析

王佳宁 , 许小剑

北京航空航天大学北京 100191

2015-05-05收到

基金项目：国家部委基金资助课题

作者简介：王佳宁(1988–)，女，籍贯甘肃会宁，现为北京航空航天大学电子信息工程学院博士研究生。主要研究方向为海面电磁散射特性仿真及分析。E-mail: manjiaqw@126.com
许小剑(1963–)，男，籍贯江西万安，博士，现为北京航空航天大学电子信息工程学院信号与信息处理学科责任教授，博士生导师。主要研究方向为遥感特征建模、分析与处理、雷达成像与目标识别、智能化信息处理等。E-mail: xiaojianxu@buaa.edu.cn

通讯联系人, 许小剑 xiaojianxu@buaa.edu.cn

摘要：该文基于加权曲率近似方法(Weighted Curvature Approximation, WCA)，实现了对2维线性与非线性海面的宽带电磁散射信号的仿真，并通过大量的蒙特卡洛仿真研究了距离高分辨率条件下各距离单元内海杂波统计特性，特别是尖峰特性。研究结果表明，当雷达分辨率提高、雷达入射视线方向由侧风转向逆风、海面风速增加时，海杂波强度概率密度曲线(Probability Density Function, PDF)的长拖尾现象将更加明显。同时，非线性海面的宽带散射回波信号中出现尖峰现象的概率更高。此外，对海杂波统计分布曲线的拟合结果表明，与传统的K分布和Weibull分布相比，Pareto分布在较小擦地角条件下能够更好描述海杂波强度的统计特性。

关键词： 2维海面宽带散射统计特性加权曲率近似方法(WCA) Pareto分布

Simulation and Analysis for Wide-band Scattering Characteristics of 2-D Linear and Nonlinear Sea Surfaces

Wang Jia-ning, Xu Xiao-jian

Beihang University, Beijing 100191, China

Abstract: In this paper, the wideband backscattering fields of two-Dimensional (2-D) linear and nonlinear sea surfaces are numerically simulated employing the Weighted Curvature Approximation (WCA) method. A large number of Monte Carlo trials are performed to investigate the statistical characteristics of the rang-resolved sea clutter, especially for the sea spike phenomenon. Simulation results demonstrate that the long tail of the sea clutter intensity Probability Density Function (PDF) tends to be more evident with finer radar resolution, higher wind speed, and when the radar sight changes from the crosswind direction to the upwind direction. Meanwhile, it is found that the nonlinear sea surfaces are more likely to have sea spikes. In addition, the Pareto distribution is demonstrated to describe the statistics of the sea clutter intensities better than the K-distribution and Weibull distribution at low grazing angles.

Key words: 2-D sea surfaces Wide-band scattering Statistical characteristics Weighted Curvature Approximation (WCA) Pareto distribution

1 引言

海面的宽带电磁散射特性研究对海背景下的雷达系统设计和海面目标检测与识别具有重要意义，特别是对易受海尖峰干扰的弱小目标检测。为掌握海面的宽带电磁散射特性，相关机构基于机载、星载等多种雷达，对海面回波信号进行了多次测量和分析^{[1, 2, 3, 4, 5]}，并得到了一些有用的结论。然而，由于测量所得数据变化范围较大，雷达系统参数、测量设备性能和海洋环境参数不一致、数据量有限等原因，基于电磁计算方法对海面宽带回波信号进行仿真对全面认识海面回波特性仍然十分必要。

目前基于电磁计算方法对海面宽带散射回波的仿真和研究主要限于1维海面。Toporkov等人^[6]利用快速迭代法(Method of Multiple Interactions,MOMI)对1维Creamer海面的宽带回波信号进行了仿真，得到了各个距离单元内的海杂波数据，并对海杂波幅度在不同雷达波段、距离分辨率、极化方式、入射角和风速下的统计分布特性进行了比较。Johnson^{[7, 8]}等人同样仿真得到1维时变海面的宽带回波信号和1维距离像，并研究了各距离单元内海杂波强度与多普勒中心频率、海面高度之间的关系。

本文基于电磁散射计算方法对2维海面的宽带电磁散射信号进行仿真，同时就宽带散射条件下海杂波数据的统计特性，尤其是尖峰特性，进行了分析和讨论。本文首先利用线性、尖峰模型(Choppy Wave Model,CWM)和Creamer(2) 3种海面模型来生成海面轮廓的高度信息，随后利用WCA方法计算得到海面在宽带入射信号各个采样频点下的散射场，继而通过对海面宽带散射的频域响应做逆傅里叶变换得到海面在时域中的宽带散射信号和1维距离像。基于此种方法，本文对不同海面模型、分辨率和风向角下的2维海面宽带散射信号进行了大量蒙特卡洛仿真，利用K分布、Weibull分布和Pareto分布等不同统计模型对海杂波强度的统计分布曲线进行了拟合，讨论和分析了海面宽带散射特性，尤其是海尖峰特性，受海面模型、雷达分辨率、海面风速和风向等因素的影响。

2 海面生成模型

比较和分析不同海面模型的电磁散射特性，能够了解水动力学作用给海面电磁散射特性带来的影响，有助于掌握和理解海杂波的散射机理。在各种海面高度生成模型中，目前最为成熟和常用的是线性海面模型。基于不同的水动力学机理，学者们建立了多种非线性海面模型，Creamer模型^[10]和CWM模型^[12]是其中应用较为广泛的两种，它们分别将线性海面高度的希尔伯特变换分量引入到波数域分量和采样点水平位移中，具有明显的Stokes波非线性特征。

线性海面将稳态无限深的风生海面视作若干幅度服从高斯分布、向不同方向传播，且相互独立的谐波的叠加，它在r=(x,y)处的高度值ζ_L(r)为^[9]：

${\zeta _{\rm{L}}}\left({r} \right) = \frac{1}{{{L_x}{L_y}}}\sum {{A_{\rm{L}}}\left( {K,{t_0}} \right)\exp\left[ {jK \cdot r} \right]}$

(1)

式(1)中，L_x和L_y分别为海面在x轴和y轴的长度；A_L(K)为t₀时刻海面在空间波数域中的分量：

$\eqalign{ & {A_{\rm{L}}}\left( K \right) = G\left( K \right)\pi \cdot \sqrt {2{L_x}{L_y}W\left( K \right)} {\rm{exp}}\left[ {{\rm{j}}\omega \left( K \right) \cdot {t_0}} \right] \cr & \qquad \qquad \; + {G^*}\left( { - K} \right)\pi \cdot \sqrt {2{L_x}{L_y}W\left( { - K} \right)} \cr & \qquad \qquad \; \cdot {\rm{exp}}\left[ { - {\rm{j}}\omega \left( K \right) \cdot {t_0}} \right] \cr}$

(2)

其中，W(K)是海面在空间波数域采样点K=(K_X,K_Y)处的海谱值，本文中选用PM海谱^[11]生成海面；K=|K|; w(K)是波数为K的谐波分量的色散因子；G(K)为满足复高斯分布的随机变量，其均值为0、方差为1；“*”为共轭符号；t₀为海面的采样时刻。

Creamer海面将线性海面高度的希尔伯特(Hilbert)变换引入到波数域分量中^[10]，其空间波数域分量为：

${A_{{\rm{Creamer}}}}\left( K \right) \! \! = \! \! \int {\frac{{\exp \left[ {jK \cdot D\left( r \right)} \right] - 1}}{K}} \exp \left[ { - jK \cdot r} \right]dr$

(3)

其中D(r)为线性海面的2维希尔伯特变换。为提高2维Creamer海面生成效率，Soriano等^[11]将式(3)中的积分项进行泰勒级数展开，取其前两阶项进行近似处理，得到Creamer(2)海面的频域分量：

$\begin{aligned} {A_{{{\rm{C}}^2}}}\left( K \right) \! = \! \! & {A_{\rm{L}}}\left( K \right) - \frac{{{K_X^2}}}{{2K}}{f^D}\left[{{D_x}{{\left( r \right)}^2}} \right] - \frac{{{K_X}{K_Y}}}{K}\\ & \! \! \cdot {f^D}\left[{{D_x}\left( r \right){D_y}\left( r \right)} \right] - \frac{{{K_Y^2}}}{{2K}}{f^D}\left[{{D_y}{{\left( r \right)}^2}} \right] \end{aligned}$

(4)

其中， $f^D$ 代表傅里叶变换，D_x(r)和D_y(r)为D(r)在x轴和y轴的分量。

CWM海面^[12]基于简化的相位扰动理论，将线性海面的希尔伯特变换视为扰动项来体现海浪间的非线性作用，其与线性海面之间存在如下映射关系：

${\zeta _{{\rm{CWM}}}}\left[{r + D\left( r \right)} \right] = {\zeta _{\rm{L}}}\left( r \right)$

(5)

可见，CWM海面是一种采样间隔非均匀的海面模型。尽管CWM海面只包含了低阶的非线性作用，但其具有明显的非线性特征，且生成效率高，模型稳定实用。

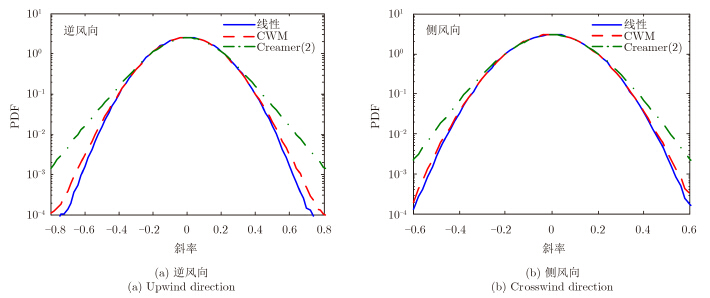
图 1对风速7 m/s时线性海面、CWM海面和Creamer(2)海面的斜率统计分布特性进行了比较。由图 1可见，受非线性作用的影响，Creamer(2)海面和CWM海面中海浪出现陡峭波面，即大斜率波浪的概率高于线性海面，且Creamer(2)海面中较大斜率出现的概率最高。特别指出，由于CWM海面采样间隔不均匀，本文利用随机过程的特征函数与PDF互为傅里叶变换对的性质，基于特征函数求得了这3种海面的斜率统计分布曲线。此外，由图 1还可看到2维海面沿逆风向的轮廓较沿侧风向的轮廓更容易出现较大的斜率，即2维海面沿逆风向的波浪形状更为尖锐。

图 1 2维线性海面、CWM海面和Creamer(2)海面斜率的统计分布 Fig.1 The statistical distribution of slopes for the 2-D linear,CWM,and Creamer(2) sea surfaces

3 海面宽带回波信号生成 3.1 WCA电磁散射计算方法

WCA方法^[13]由Elfouhaily等人提出，其将海面曲率引入到积分式的核函数中，可在某些限定条件下转换为微扰法(Small Perturbation Method,SPM)或者基尔霍夫近似法(Kirchhoff Approximation,KA)。WCA方法的计算精度较高，能够正确反映不同极化方式下的海面散射场的相位，在近几年得到了充分关注。

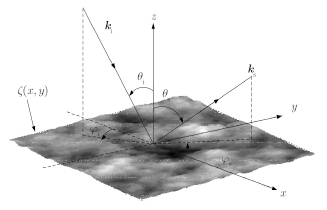
图 2为2维海面的电磁散射几何示意图。其中，θ_i和θ_s为入射角和散射角；φ_i和φ_s为入射方位角和散射方位角；k_i和k_s为入射波矢量和散射波矢量。在本文所考虑的后向散射条件下，k_i=-k_s。为方便数学表述，引入Ewald向量Q=k_s-k_i，记其在水平面和z轴上的投影分别为Q_H和Q_z。同时，为了减小海面尺寸截断带来的误差，引入时域锥形入射波I(r,θ)^[14]。随着坐标点远离照射中心，它所定义的入射场强度以高斯函数的形式衰减为零。本文中，设定锥形波参数为max(L_x,L_y)/6。

图 2 2维海面电磁散射几何示意图 Fig.2 Geometry configuration for the wave scattering from 2-D surface

WCA的计算式如式(6)所示^[13]：

$\begin{aligned} S\left( f \right) = \frac{1}{{{{\left( {2π} \right)}^2}{Q_z}\sqrt {{P_{{\rm{inc}}}}} }}\int {I\left( {r,\zeta } \right)\left\{ {B - T\left( {\nabla \zeta } \right)} \right\}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \\ \cdot {\rm{exp}}\left[{ - {\rm{j}}{Q_{\rm{H}}} \cdot r - {\rm{j}}{Q_z}\zeta (r)} \right] {\rm{d}}r \end{aligned}$

(6)

式(6)中，

$\nabla \zeta$ 为海面高度的梯度；P_inc为照射到海面的入射场总能量；函数B为Bragg张量。核函数T受到海面曲率的影响，反映基尔霍夫核K与Bragg张量B之间的差异，本文中定义为^[13]：

$T\left( {\nabla \zeta } \right) = \left( {B - K} \right)\frac{{{Q_z^2}}}{{{Q_{\rm{H}}^2}}}{\left( {\nabla \zeta } \right)^2}$

(7)

其中，Q_H和Q_z为矢量Q_H和Q_z的模值。

对于采样间隔非均匀的CWM海面，将采样点坐标(r+D(r),ζ_L(r))代入式(6)，得：

$\eqalign{ & S(f{\rm{ }}){\rm{ = }}{1 \over {{{{\rm{(2}}\pi {\rm{ )}}}^{\rm{2}}}{\rm{ }}{Q_z}\sqrt {{P_{inc}}} }}\int {I(\tilde r{\rm{ ,}}{\zeta _{CWM}}{\rm{ }}(\tilde r))} \cr & \; \; \; \; \; \; \; \;\; \cdot \{ B - T(\nabla {\zeta _{CWM}}{\rm{ }}(\tilde r))\} \cr & \; \; \; \; \; \; \; \; \;\cdot \exp [ - j{Q_H} - \tilde r - j{Q_{z\zeta CWM}}(\tilde r)]d\tilde r \cr}$

(8)

注意到非线性映射关系

$\tilde r \to r + D\left( r \right)$ 转换的雅克比矩阵J(r)为：

$J \!\! \left( r \right) = \left| \!\! {\begin{array}{*{20}{c}} { 1 + {\partial _x}{D_x}\left( r \right)} & {{\partial _x}{D_y}\left( r \right)}\\ {{\partial _y}{D_x}\left( r \right)} & {1 + {\partial _y}{D_y}\left( r \right)} \end{array}} \!\! \right|$

(9)

且CWM海面在r+D(r)处的梯度为：

$\nabla {\zeta _{{\rm{CWM}}}}\left[{r + D \! \left( r \right)} \right] = J \! {\left( r \right)^{ - 1}}\nabla {\zeta _{\rm{L}}}\left( r \right)$

(10)

将式(9)与式(10)代入式(6)后可得到采样间隔非均匀的CWM的散射场：

$\begin{array}{l} S\left( f \right) = \frac{1}{{{{\left( {2\pi } \right)}^2}{Q_z}\sqrt {{P_{{\rm{inc}}}}} }}\int {I\left[ {r + D\left( r \right)} \right]J\left( r \right)} \\ \qquad \qquad \cdot \left\{ {B - T\left( {J{{\left( r \right)}^{ - 1}}\nabla {\zeta _{\rm{L}}}\left( r \right)} \right)} \right\} \\ \qquad \qquad \cdot {\rm{exp}}\left\{ { - {\rm{j}}{Q_{\rm{H}}} \cdot \left[ {r + D\left( r \right)} \right] - {\rm{j}}{Q_z}{\zeta _{\rm{L}}}\left( r \right)} \right\}{\rm{d}}r \end{array}$

(11)

3.2 海面宽带时域回波信号生成

为获得海面在各个距离单元内的海杂波数据，首先需要对海面的宽带电磁散射回波信号进行仿真。然而，目前关于粗糙面的电磁散射计算方法大多是在点频下进行。因此，本文首先基于3.1节介绍的WCA方法计算得到海面在入射信号频域中各个采样点下的散射场，再通过逆傅里叶变换得到海面在时域中的宽带散射信号。记海面在频点f处的散射场为S(f)，雷达发射信号的窗函数为H(f)，则海面在时域的宽带散射信号为：

$s \! \left( t \right) = \int_{ - \infty }^\infty {H\left( f \right)S \! \left( f \right)\exp \left( {{\rm{j}}2π ft} \right){\rm{d}}f}$

(12)

考虑到雷达信号的双程时延效应，不难获知t时刻的回波信号对应着地距为r_g=ct/2sin_i处的海面散射信号，其中c为电磁波传播速度，_i为雷达入射角。由于在电磁散射计算中采用了锥形窗函数，直接对S(f)做逆傅里叶变换后得到的海面在时域回波信号幅度同样受到锥形窗函数的包络。为方便去除锥形窗函数的影响，假设雷达入射波矢量在水平面上的投影沿着x轴。如此，对海面时域回波信号s(t)除以锥形波幅度在y轴上的积分即可得到去除锥形窗影响后的海面回波信号。

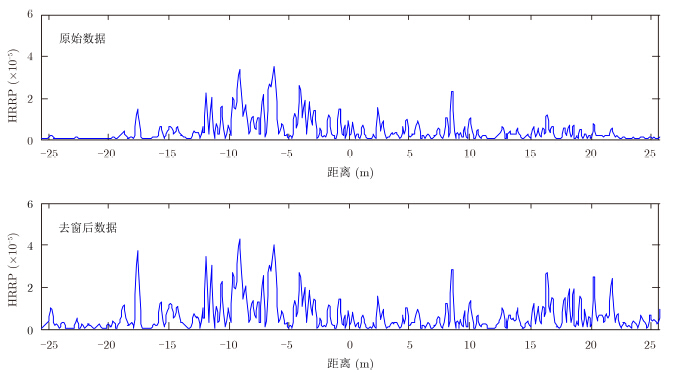
图 3给出某幅随机选取的Creamer(2)海面在入射角84º时，由海面宽带散射回波信号直接所得和去除锥形窗影响后得到的海面1维距离像。海面风速为5 m/s，极化方式为HH，风向与x轴指向相反。雷达入射中心频率为1 GHz，带宽为400 MHz，仿真中海面尺寸为153.6 m×153.6 m。由于边缘处锥形窗影响无法完全消除，图 3只给出海面照射中心1/3处的海面1维距离像。由图 3可见，由海面原始宽带散射回波信号直接得到的海面1维距离像明显受到锥形窗函数的影响，远离照射中心区域的海面回波信号强度十分微弱。当去除锥形窗影响之后，远离照射中心区域处的海面回波信号特征也开始变得明显。

图 3 锥形窗影响去除前后得到的海面1维距离像 Fig.3 1-D range-resolved sea clutter profiles before and after removing the tapered window

4 海杂波的统计分布模型

在传统的海杂波强度分布模型中，Weibull分布和K分布应用十分广泛^[15]。其中，Weibull分布建立在测量数据的基础上，而K分布与海面回波的调制机理相对应。在高分辨率雷达系统下，当擦地角较小时，海面的回波信号会出现尖峰现象，即高幅度杂波出现的概率增大，导致杂波概率密度函数的拖尾加长。此时，Weibull分布和K分布与实际杂波的概率密度分布在1-CDF水平较小的时候会出现偏离。近年来，Pareto分布得到很多关注^[16]，其相较于Weibull分布和K分布有更长的拖尾，与实际海杂波分布吻合更好，且其数学形式较为简单，在实际应用中更为方便。

Pareto分布模型的构成与K分布相同，其概率密度函数可写为：

$P(u) = \int\nolimits_0^{ + \infty } {P(u|v)P(u){\rm{d}}u}$

(13)

其中，u服从形状参数为a，尺寸参数为b的逆伽马分布，它可看作海杂波的纹理分量，调制着服从负指数分布的散斑分量v。散斑分量v和纹理分量u的概率密度函数分别为：

$P(v|u) = \frac{1}{u}\exp \left( - \frac{v}{u}\right) \hspace{37pt}$

(14)

$P\left( u \right) = \frac{{{b^a}}}{{\Gamma \! \left( a \right)}}{u^{ - a - 1}}\exp \left( { - \frac{b}{u}} \right)$

(15)

将式(14)和式(15)代入到式(13)中，得到Pareto分布的概率密度函数：

$\begin{aligned} P(v) = & \frac{{{b^a}}}{{\Gamma \! \left( a \right)}}\int\nolimits_0^{ + \infty } {{u^{ - a - 2}}\exp \left( { - \frac{{v + b}}{u}} \right)} {\rm{d}}u \\ = & \frac{{a{b^a}}}{{{{\left( {b + v} \right)}^a}}} \end{aligned}$

(16)

Pareto分布的形状参数和尺寸参数可由式(17)与式(18)估计得到：

$\hat a = \frac{{2{{\left\langle v \right\rangle }^2}}}{{2{{\left\langle v \right\rangle }^2} - \left\langle {{v^2}} \right\rangle }}$

(17)

$\hat b = (\hat a - 1)\left\langle v \right\rangle \hspace{12pt}$

(18)

Pareto分布的形状参数越小，概率密度函数的形状越为尖锐，长拖尾现象越严重。

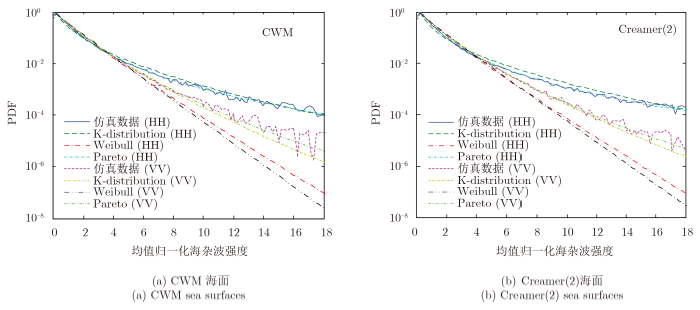
图 4基于2维CWM海面和Creamer(2)海面生成了海面宽带散射信号，分别利用K分布、Weibull分布和Pareto分布模型对各距离单元内海杂波强度的PDF曲线进行了拟合。图 4中海面上空风速为7 m/s，风向与雷达视线方向相反，入射角为80º。由图 4可见，相比于K分布和Weibull分布，Pareto分布能够更好地对海杂波统计分布曲线进行描述，尤其是海尖峰所对应的、杂波强度较大处的PDF尾部区域。这与文献^[16]中对实测海杂波数据进行拟合和分析得到的结论一致。

图 4 不同分布模型对海面回波信号强度的拟合结果 Fig.4 Fitted PDFs of the normalized range-resolved sea clutter intensities with different distribution models

5 仿真结果及分析

为讨论和分析宽带散射条件下的海杂波幅度特性，特别是尖峰对海杂波幅度特性带来的影响，本文对不同海面模型、分辨率、风向和风速下的海面宽带散射信号进行了仿真和比较。对海尖峰的判别^{[17, 18, 19, 20]}可利用多种参数，本文从散射强度出发，对符合海尖峰散射强度要求的散射点进行判别，将其视为海尖峰。仿真中设定雷达中心频率为1 GHz，带宽为400 MHz，过采样率1.2倍，海面尺寸为153.6 m×76.8 m，空间采样间隔为最高入射频率处波长的1/8，蒙特卡洛数为2000。由于锥形窗边缘处的影响无法完全去除，截取海面中心1/3处的回波数据进行统计和分析。

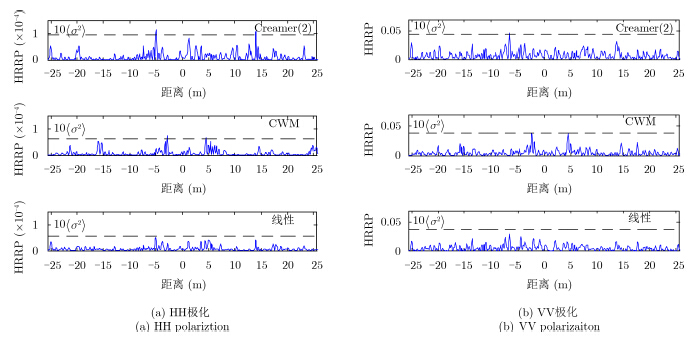
为比较海面模型对海杂波散射特性的影响，图 5对同组随机数仿真得到的线性海面、CWM海面和Creamer(2)海面的1维距离像进行了对比。图 5中海面上空风速为7 m/s，雷达入射角为80º，入射方向为逆风向。图 5中虚线为海尖峰强度检测阈值，定义为10倍的海杂波强度均值^[20]。由图 5可见，相同条件下，Creamer(2)海面中强散射点现象最明显，而线性海面回波信号中强散射点现象最弱。同时，HH极化下仿真所得海面回波信号较VV

图 5 2维Creamer(2)海面、CWM海面和线性海面的1维距离像 Fig.5 1-D range-resolved sea clutter profiles from 2-D Creamer(2),CWM and linearsea surfaces

极化下更容易出现满足海尖峰散射强度要求的散射点。图 6为相同仿真条件下，3种海面宽带回波信号强度的统计分布曲线。在图 6中，可观察到Creamer(2)海面在远大于回波强度均值处具有最大的PDF值，其长拖尾现象最严重。而线性海面在回波强度较大值处的PDF值最小，对应的形状参数也最大。由电磁散射理论可知，海面的电磁散射强度会随着入射角的增大而减小，特别是在HH极化下。相同仿真条件下，非线性海面的波峰更为陡峭，这使得非线性海面中波峰附近的局部入射角小于线性海面中同一波峰附近的局部入射角，继而导致非线性海面中此位置附近的电磁散射强度增大。注意到非线性海面中出现斜率较大的波面概率更大，因此，非线性海面中更容易出现强散射点。由于Creamer(2)海面中出现大斜率波浪的概率最大，因而Creamer(2)海面中的尖峰现象最为显著。

图 6 2维线性海面、CWM海面和Creamer(2)海面宽带散射回波信号强度的PDF PDFs of the wide-band scattering intensities from 2-D linear,CWM and Creamer(2) sea surfaces

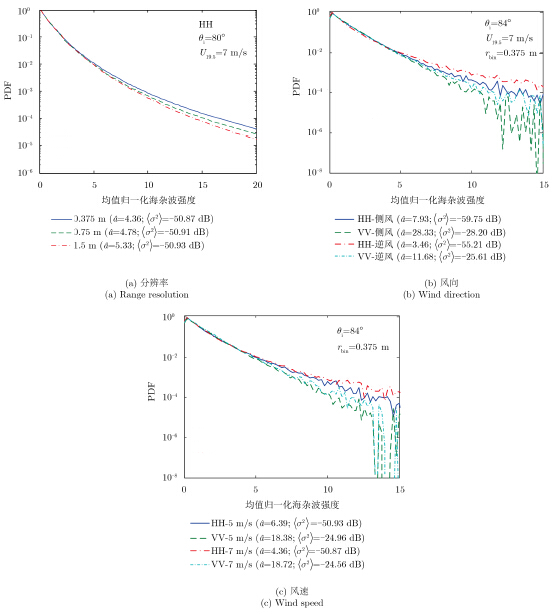
图 7(a)-图 7(c)以CWM海面为例，分别比较了雷达分辨率、风向和风速对海杂波强度统计特性的影响。图 7(a)中雷达入射角为80º，海面风速7 m/s，风向为逆风，极化方式为HH；图 7(b)中雷达入射角为84º，风速7 m/s，分辨率0.375 m；图 7(c)中雷达入射角为84º，风向为逆风，分辨率0.375 m。由图 7可见，随着雷达分辨率的提高、风向由侧风转向逆风、风速的增加，海杂波强度PDF的长拖尾现象更加明显，基于Pareto模型估计所得的海杂波强度PDF的形状参数也随之减小。这与Toporkov等人^[6]对1维海面宽带散射特性进行仿真和对实测数据进行分析得到的结论^[21]一致。

图 7 2维CWM海面宽带散射信号强度在不同分辨率、风向和风速下的PDF PDFs of the wide-band scattering intensities from 2-D CWM sea surfaces under different range resolutions,wind directions and wind speeds

由于各距离单元内海杂波散射场相当于该单元内各散射点的散射贡献之和，当雷达分辨率提高时，单个距离单元中的散射点个数减小，由中心极限定理可知，此时各距离单元中的海杂波散射场偏离复高斯分布的程度更为显著，从而导致海杂波PDF的长拖尾现象随着分辨率提高而更加严重。另一方面，由图 1可知，2维海面中海浪斜率的分布特性在各个方向不是相同的，较大的斜率更多地出现在与风向一致的波浪切片而非与风向垂直的切片上，即平行于风向的海面轮廓较垂直于风向的海面轮廓更为尖锐。同时当海面粗糙度随风速增加而提高时，波浪的轮廓也随之变得更为尖锐。因此，海杂波的尖峰特性会随风向由侧风向逆风转变和风速的提高而更为显著，且其平均散射强度也有所增加。

6 结论

本文基于WCA电磁散射计算方法，实现了对2维线性、CWM和Creamer(2)海面的宽带电磁散射信号的仿真，并对海面宽带散射信号强度的统计特性，尤其是尖峰特性，进行了分析和讨论。仿真结果表明，当雷达分辨率提高、海面上空风速变大、入射视线方向由侧风转向逆风时，海面宽带散射信号中的出现强散射点的现象将越加明显。同时，受海浪间非线性作用的影响，Creamer(2)海面的回波信号中强散射点现象最为显著，而线性海面回波中尖峰现象最弱。此外，对海面回波强度PDF的拟合结果表明，Pareto分布能够很好地描述其统计分布特性。

参考文献

[1]	Antipov I. Statistical analysis of northern Australia coastline sea clutter data[R]. DSTO-TR-1236, 2001.(1)
[2]	Fuchs J, Regas D, Waseda T, et al.. Correlation of hydrodynamic features with LGA radar backscatter from breaking waves[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2442-2460.(1)
[3]	Ward K D, Baker C J, and Watts S. Maritime surveillance radar part 1: radar scattering from the ocean surface[J]. IEE Proceedings F Radar and Signal Processing, 1990, 137(2): 51-62.(1)
[4]	Nohara T J and Haykin S. Canadian east coast radar trials and the K-distribution[J]. IEE Proceedings F Radar and Signal Processing, 1991, 138(2): 80-88.(1)
[5]	Haykin S, Krasnor C, Nohara T J, et al.. A coherent dualpolarized radar for studying the ocean environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 1991, 29(1): 189-191.(1)
[6]	Toporkov J V and Sletten M A. Statistical properties of low-grazing range-resolved sea surface backscatter generated through two-dimensional direct numerical simulations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5): 1181-1197.(2)
[7]	Johnson J T, Burkholder R J, Toporkov J V, et al.. A numerical study of the retrieval of sea surface height profiles from low grazing angle radar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(7): 1641-1650.(1)
[8]	Chae C S and Johnson J T. A study of sea surface rangeresolved Doppler spectra using numerically simulated lowgrazing- angle backscatter data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3452-3460.(1)
[9]	Tessendorf J. Simulating Ocean Water[R]. Simulating Nature: Realistic and Interactive Techniques, SIGGRAPH 2001 Course Notes 47.(1)
[10]	Creamer D B, Henyey F, Schult R, et al.. Improved linear representation of ocean surface waves[J]. Journal of Fluid Mechanics, 1989, 205: 135-161.(2)
[11]	Soriano G, Joelson M, and Saillard M. Doppler spectra from a two-dimensional ocean surface at L-band[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(9): 2430-2437.(2)
[12]	Nouguier F, Guérin C A, and Chapron B. “Choppy Wave” model for nonlinear gravity waves[J]. Journal of Geophysical Research, 2009, 114: 1-16.(2)
[13]	Guérin C A, Soriano G, and Charpon B. The weighted curvature approximation in scattering from sea surfaces[J]. Waves in Random and Complex Media, 2010, 20(3): 364-384.(3)
[14]	Thorsos E I. The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum[J]. Journal of Acoustical Society of America, 1988, 83(1): 78-92.(1)
[15]	Ward K D, Tough R J A, and Watts S. Sea Clutter: Scattering, the K Distribution and Radar Performance[M]. London, U. K.: The Institution of Engineering and Technology, 2006: 106-129.(1)
[16]	Farshchian M and Posner F L. The Pareto distribution for low grazing angle and high resolution X-band sea clutter[C]. Proceedings of IEEE Radar Conference, 2010: 789-793.(2)
[17]	Chen X, Guan J, Bao Z, et al.. Detection and extraction of target with micromotion in spiky sea clutter via short-time fractional Fourier transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1002-1018.(1)
[18]	Melief H W, Greidanus H, Genderen P, et al.. Analysis of sea spikes in radar sea clutter data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(4): 985-993.(1)
[19]	Greco M, Stinco P, and Gini F. Identification and analysis of sea radar clutter spikes[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 239-250.(1)
[20]	Liu L and Frasier S J. Measurement and classification of low grazing angle radar sea spikes[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(1): 27-40.(2)
[21]	Moya J C, Menoyo J G, Campo á B, et al.. Statistical analysis of a high-resolution sea-clutter database[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2024-2037.(1)

本文献在全文中的定位：

...构基于机载、星载等多种雷达，对海面回波信号进行了多次测量和分析^{[1, 2, 3]},...[View in article]

本文献在全文中的定位：

...面回波信号进行了多次测量和分析^{[1, 2, 3, 4]}, ...[View in article]

本文献在全文中的定位：

...^{[1, 2, 3, 4, 5]}...[View in article]

本文献在全文中的定位：

..., ^{[2, 3, 4, 5]}，并得到了一些有用的结论。然而...[View in article]

本文献在全文中的定位：

..., ^{[3, 4, 5]}，并得到了一些有用的结论。然而，由于测量所得数据变化范围较大，...[View in article]

本文献在全文中的定位：

...算方法对海面宽带散射回波的仿真和研究主要限于1维海面。Toporkov等人^[6]利用快速迭代法(Method of Multiple Interactions,MOMI)对1维Creamer海面的宽带回...[View in article]

...to模型估计所得的海杂波强度PDF的形状参数也随之减小。这与Toporkov等人^[6]对1维海面宽带散射特性进行仿真和对实测数据进行分析得到的结论^{...[View in article]}

本文献在全文中的定位：

...分辨率、极化方式、入射角和风速下的统计分布特性进行了比较。Johnson^{[7, 8]}等人同样仿真得到1维时变海面的宽...[View in article]

本文献在全文中的定位：

...的统计分布特性进行了比较。Johnson^{[7, 8]}等人同样仿真得到1维时变海面的宽带回波信号和1维距离像，并研究了...[View in article]

本文献在全文中的定位：

...它在r=(x,y)处的高度值ζ_L(r)为^[9]：...[View in article]

本文献在全文中的定位：

...于不同的水动力学机理，学者们建立了多种非线性海面模型，Creamer模型^[10]和CWM模型^[12]是其中应用较为 ...[View in article]

...Creamer海面将线性海面高度的希尔伯特(Hilbert)变换引入到波数域分量中^[10]，其空间波数域分量为：...[View in article]

本文献在全文中的定位：

...K=(K_X,K_Y)处的海谱值，本文中选用PM海谱^[11]生成海面；K=|K|; w(K)是波数为K的谐波分量的...[View in article]

...为线性海面的2维希尔伯特变换。为提高2维Creamer海面生成效率，Soriano等^[11]将式(3)中的积分项进行泰勒级数展开，取其前两阶项进行近似处理，得...[View in article]

本文献在全文中的定位：

...模型，Creamer模型^[10]和CWM模型^[12]是其中应用较为广泛的两种，它们分别将线性海面高度的希尔伯特变换...[View in article]

...为D(r)在x轴和y轴的分量。CWM海面^[12]基于简化的相位扰动理论，将线性海面的希尔伯特变换视为扰动项来体...[View in article]

本文献在全文中的定位：

...WCA方法^[13]由Elfouhaily等人提出，其将海面曲率引入到积分式的核函数中，可在某...[View in article]

...surface WCA的计算式如式(6)所示^[13]：...[View in article]

...响，反映基尔霍夫核K与Bragg张量B之间的差异，本文中定义为^[13]...[View in article]

本文献在全文中的定位：

...寸截断带来的误差，引入时域锥形入射波I(r,θ)^[14]。随着坐标点远离照射中心，它所定义的入射场强度以高斯函数的形式...[View in article]

本文献在全文中的定位：

...在传统的海杂波强度分布模型中，Weibull分布和K分布应用十分广泛^[15]。其中，Weibull分布建立在测量数据的基础上，而K分布与海面回波的调...[View in article]

本文献在全文中的定位：

...布在1-CDF水平较小的时候会出现偏离。近年来，Pareto分布得到很多关注^[16]，其相较于Weibull分布和K分布有更长的拖尾，与实际海杂波分布吻合更...[View in article]

...述，尤其是海尖峰所对应的、杂波强度较大处的PDF尾部区域。这与文献^[16]中对实测海杂波数据进行拟合和分析得到的结论一致。...[View in article]

本文献在全文中的定位：

...风向和风速下的海面宽带散射信号进行了仿真和比较。对海尖峰的判别^{[17, 18, 19]} ,...[View in article]

本文献在全文中的定位：

...行了仿真和比较。对海尖峰的判别^{[17, 18, 19, 20]}...[View in article]

本文献在全文中的定位：

...^{[17, 18, 19, 20]}可利用多种参数，本文从散射强...[View in article]

本文献在全文中的定位：

...,^{[18, 19, 20]}可利用多种参数，本文从散射强度出发，对符合海尖峰散射强度要求的...[View in article]

...图 5中虚线为海尖峰强度检测阈值，定义为10倍的海杂波强度均值^[20]。由图 5可见，相同条件下，Creamer(2)...[View in article]

本文献在全文中的定位：

...对1维海面宽带散射特性进行仿真和对实测数据进行分析得到的结论^[21]一致。...[View in article]

图 1 2维线性海面、CWM海面和Creamer(2)海面斜率的统计分布 Fig.1 The statistical distribution of slopes for the 2-D linear,CWM,and Creamer(2) sea surfaces

图 2 2维海面电磁散射几何示意图 Fig.2 Geometry configuration for the wave scattering from 2-D surface

图 3 锥形窗影响去除前后得到的海面1维距离像 Fig.3 1-D range-resolved sea clutter profiles before and after removing the tapered window

图 4 不同分布模型对海面回波信号强度的拟合结果 Fig.4 Fitted PDFs of the normalized range-resolved sea clutter intensities with different distribution models

图 5 2维Creamer(2)海面、CWM海面和线性海面的1维距离像 Fig.5 1-D range-resolved sea clutter profiles from 2-D Creamer(2),CWM and linearsea surfaces

图 6 2维线性海面、CWM海面和Creamer(2)海面宽带散射回波信号强度的PDF PDFs of the wide-band scattering intensities from 2-D linear,CWM and Creamer(2) sea surfaces

返回顶部