由于海杂波对来自海面或接近海面的目标(包括低空掠海飞行的飞机、小型军舰、航海浮标以及漂浮在海上的冰块),回波的可检测性形成严重制约,因此,对海杂波的研究不仅具有理论意义,而且具有实用价值[1, 2, 3, 4]。对于通常海面而言,海浪的波高一般能达到数英尺,并且在大的波浪上还覆盖着小的风浪和毛细波,即由大尺度重力波和小尺度张力波组成,可将海面简化为仅含有两种尺度粗糙度的表面,即大尺度粗糙面和小尺度粗糙面,根据这一特性,提出了粗糙面电磁散射的双尺度模型[5]。然而,双尺度法依赖粗糙面的划分方式,且该模型仅适用于非时变的海面散射回波信号,即频率不随时间发生变化,难以描述和解释海面白浪和破碎波产生的强雷达回波。
近年来,更多的研究表明,在高分辨率雷达对海观测中,当以低掠射角(通常入射角大于85°)照射粗糙海面或高海况时,海浪失去平衡状态,出现浪花,从而产生了破碎波,破碎波的雷达反射回波表现为海尖峰[6]。此时,雷达回波强度会明显增强,表现为随机分布在不同距离、不同角度上的零星的运动或者静止目标,其PDF曲线表现出较长的“拖尾”现象,通常持续较短的时间,但在此时间范围内保持很强的相关性。由于海尖峰出现时间较短,使得海杂波由稳态向非稳态,非时变向时变转换,影响海杂波的多普勒谱,雷达有可能将海尖峰判断为一个具有一定速度的移动目标,进而导致虚警概率的增加[7]。因此,对它进行深入研究,从多角度分析海尖峰特性以及对海杂波的影响是非常必要的。
直到最近几年,国内外对海尖峰的研究才逐渐成为海杂波领域中的热门课题。文献[8]对某一时间内单个距离单元上的海尖峰发生次数进行了研究,并给出了一个平均尖峰数与海面风速之间的经验关系式。文献[9]指出雷达海尖峰主要受低擦地角、风向、雷达视角以及极化方式等因素的影响,并进行了空时2维频谱分析。文献[6]对海尖峰的统计特性进行了分析,认为幅度门限、最小间隔时间和最小尖峰宽度是描述海尖峰的3个重要因素,给出了海尖峰的判定方法。现有文献多为对海尖峰的定性描述和研究,缺乏系统的分析,尤其在国内,专门针对海尖峰特性的研究尚不多见[10, 11]。
对于海尖峰的产生目前为止并没有严格的物理解释和数学模型,但通过大量的实测数据统计试验表明,在高分辨率、低擦地角、高海况以及HH极化工作方式下容易出现海尖峰[12]。海尖峰的出现导致虚警的增加,因此,研究海尖峰的判别和抑制方法对于海面目标尤其是动目标的检测至关重要。本文首先在海尖峰判别和提取方法的基础上,结合实测海杂波数据,系统分析了不同海况和极化方式下海尖峰的幅值特性、时间相关性、多普勒谱特性以及分数阶功率谱(Fractional Power Spectrum,FPS)[13]特性;其次,提出一种基于海尖峰判别方法的海杂波抑制方法,改善信杂比(Signal-to-Clutter Ratio,SCR),从而可进一步提升雷达对微弱动目标检测能力;最后,实测数据验证了该方法的有效性。
2 海尖峰判别和提取方法为有效分析海尖峰特性,首先需要将海尖峰从杂波背景中分离出来。文献[9]基于3个特征参数提出了海尖峰的判别方法,即尖峰幅度门限Ts,最小尖峰宽度Wmin (最小尖峰持续时间)以及最小尖峰间隔Imin。对于来自于某一距离单元的海杂波时间序列,其采样点序列需满足如下3个条件才能判定为海尖峰:(1)采样点的幅度必须超过一定的门限;(2)采样点幅度连续保持在尖峰幅度门限之上的时间必须大于或等于规定的最小尖峰宽度;(3)如果高于尖峰幅度门限的连续采样点之后出现采样点的幅度低于尖峰幅度门限,那么低于门限的时间不能超过规定的最小尖峰间隔时间。
| $\left. \begin{align} & {{\left| x_{i}^{\text{HH}} \right|}^{2}}\ge T_{s}^{\text{HH}} \\ & W_{s}^{\text{HH}}\ge W_{\min }^{\text{HH}} \\ & I_{s}^{\text{HH}}\ge I_{\min }^{\text{HH}} \\ \end{align} \right\}$ | (1) |
| $T_{s}^{\text{HH}}=\frac{L}{N}\sum\limits_{i=1}^{N}{{{\left| x_{{}}^{\text{HH}}(i) \right|}^{2}}}$ | (2) |
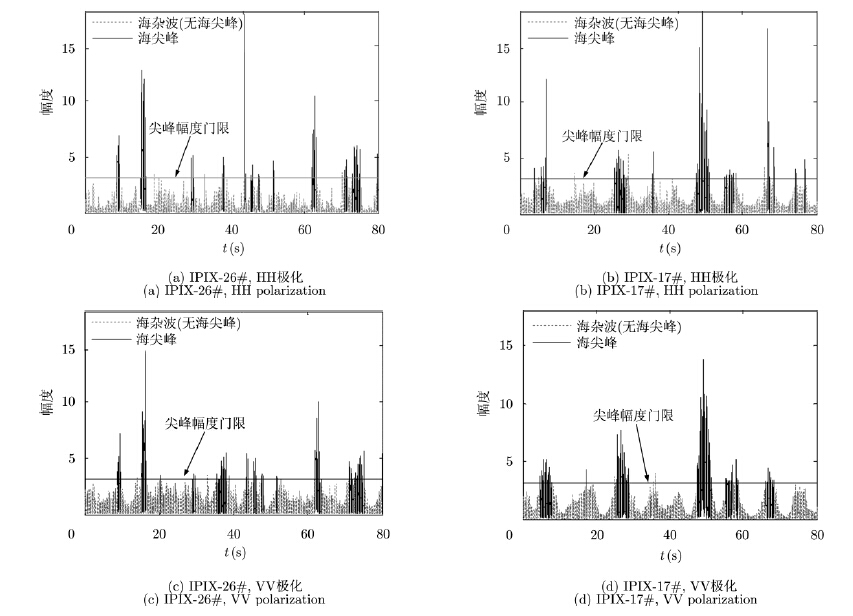
采用海尖峰的判别准则(式(1))对实测海杂波数据进行海尖峰判别和提取,本节在计算过程中采用文献[6]中的统计参数值,即最小尖峰宽度设为0.1 s,最小尖峰间隔设为0.5 s,尖峰幅度门限取为海杂波平均功率的5倍。实际应用中,判别海尖峰的3个参数并不是固定不变的,其数值往往随着观测条件和海况的变化而有所变化。采用加拿大Mcmaster大学的自适应系统实验室的X波段IPIX (Intelligent PIXel)雷达的纯海杂波数据进行分析,为了充分展示海尖峰在不同海况条件下的特性,分别选取高低两组海杂波数据进行分析,其中199311 07_135603(IPIX-17#)为较高海况数据(显著波高为2.1 m),19931108_220902(IPIX-26#)为较低海况数据(显著波高为1.0 m),数据说明详见表 1和文献[14]。图 1给出了HH和VV极化方式下的纯海杂波单元中海尖峰判别情况。图中黑色区域表示判别为海尖峰的海杂波数据,灰色虚线区域表示非海尖峰的海杂波背景数据。可以看出,海尖峰较背景杂波起伏剧烈且在HH极化方式下,回波持续时间较短,幅度高于VV极化,与目标回波较为相似,容易造成虚警。
|
图 1 海尖峰识别结果 Fig.1 Results of sea spikes identification |
| 表 1 IPIX数据描述 Tab. 1 Description of IPIX datasets |
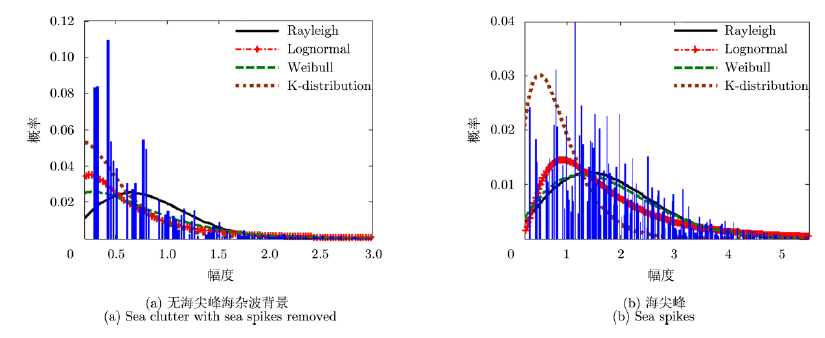
对海杂波的时域幅度分布进行直方图统计,如图 2所示,分别采用瑞利(Rayleigh)、对数正态(Lognormal)、韦布尔(Weibull)和K分布对海尖峰和海杂波背景幅度进行拟合,明显看出,海尖峰幅度的概率密度分布具有较长的“拖尾”,呈现非高斯性。表 2进一步给出了海尖峰的数量统计分析结果。Bragg散射使得VV极化方式下的海杂波背景幅度高于HH极化,而HH极化方式下的海尖峰较VV极化更为尖锐,但在数量和功率百分比方面却明显低于VV极化。对于IPIX-26#,VV极化海尖峰数量占海杂波的15.49%,而HH极化海尖峰仅有12.31%,这是因为前者的海尖峰平均持续时间长于后者,导致海尖峰数量的增多,如图 1所示。同时,通过比较两组数据统计结果,容易得出海尖峰的数量和功率百分比随海况的提高而增加。以上结论同样适用于IPIX雷达的其它组数据。
|
图 2 海杂波时域幅度分布(IPIX-17#,HH极化) Fig.2 Amplitude distribution of sea spikes in time domain (IPIX-17#,HH polarization) |
| 表 2 海尖峰数量统计(%) Tab. 2 Quantity statistics of sea spikes (%) |
当雷达固定方位和水平入射角时,海杂波的相关时间(Temporal Time,TC)可用自相关函数(Auto Correlation Function,ACF)表征,定义为[15]:
| $\text{AC}{{\text{F}}_{n}}={\sum\limits_{i=1}^{N-1}{{{x}_{i}}x_{i+n}^{*}}}/{\sum\limits_{i=1}^{N-1}{{{x}_{i}}x_{i}^{*}}}\;$ | (3) |
表 3给出了海尖峰和海杂波背景(无海尖峰)的统计相关时间,IPIX-26#较IPIX-17#的海尖峰有更长的相关时间,进一步证明低海况通常伴随较长的相关时间。图 3比较了HH和VV极化方式IPIX-17#海杂波的相关性,可知海尖峰的相关时间通常略长于不含海尖峰的海杂波背景,同时HH极化下的海尖峰相关时间(32 ms)长于VV极化(16 ms)。从图 3(b)也可以发现,VV极化方式下海尖峰和海杂波背景的相关时间相近,这是由于海杂波在VV极化时幅度起伏剧烈,导致相关性降低。以上得到的统计结论与文献[16]采用的X波段Racal- Thorn Wells海用雷达对海杂波中的Bragg、白帽和海尖峰分量的试验分析结果相似。
| 表 3 海尖峰相关时间统计 Tab. 3 ACF of sea spikes |

|
图 2 海杂波相关性(IPIX-17#) Fig.2 ACF property of sea clutter (IPIX-17#) |
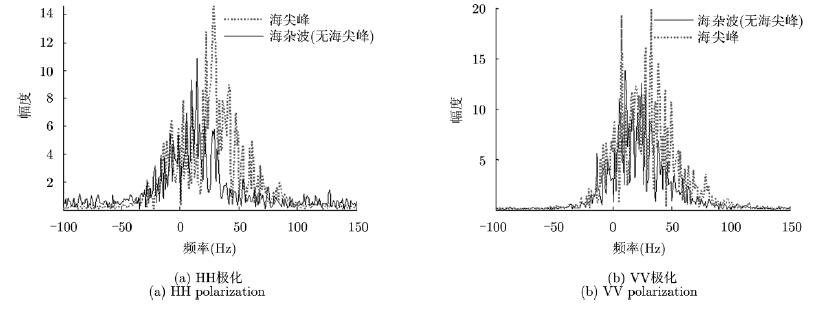
对HH和VV极化海尖峰和海杂波背景的多普勒谱进行分析,如图 4所示。可以看到海尖峰较海杂波背景的多普勒谱展宽,不仅从幅度和多普勒频率均高于海杂波背景,尤其是HH极化海尖峰更为明显。进一步采用短时傅里叶变换(Short-Time Fourier Transform,STFT)分析海杂波的时频特性,如图 5所示,右侧亮度条对应幅值大小,可以观测到无海尖峰的海杂波背景多普勒能量主要集中在中心频率附近(约为30~40 Hz),主要体现为大尺度波的Bragg散射,而海尖峰的多普勒谱发生明显偏移和展宽,主要体现为“快变信号”的非Bragg散射,使得回波散射截面积起伏,多普勒频率随时间变化,表现出明显的非平稳和时变特性。同时,发现在HH极化工作方式下,海尖峰的总体功率水平相对较弱,但此时海尖峰的时变特性更为明显。
|
图 4 海杂波多普勒谱(IPIX-17#,N=512) Fig.4 Doppler spectrum of sea clutter (IPIX-17#,N=512) |

|
图 5 海杂波STFT谱(IPIX-17#,N=512) Fig.5 STFT spectrum of sea clutter (IPIX-17#,N=512) |
分数阶功率谱(FPS)可通过分数阶相关函数的分数阶傅里叶变换(FRactional Fourier Transform,FRFT)运算得到,是传统理论在FRFT域的广义形式[13]。FPS非常适合分析时变随机信号,能够从本质上反映海面散射回波信号的功率谱密度在FRFT域的变化和能量分布,进而分析“快变信号”的非Bragg谱特性[7],如海尖峰。随机信号$\xi (t)$的FPS可表示为:
| $P_{\xi }^{\alpha }(u)={{A}_{-\alpha }}{{F}_{\alpha }}[R_{\xi }^{\alpha }(\tau )](u){{\text{e}}^{-\text{j}\frac{{{u}^{2}}}{2}\cot \alpha }}$ | (4) |
| $\begin{align} & R_{\xi }^{\alpha }(\tau )=\underset{T\to \infty }{\mathop{\lim }}\,\frac{1}{2T}\int_{-T}^{T}{{{R}_{\xi }}({{t}_{2}}+\tau ,{{t}_{2}}){{\text{e}}^{\text{j}{{t}_{2}}\tau \cot \alpha }}\text{d}{{t}_{2}}} \\ & \qquad \ \ ={{\left\langle {{R}_{\xi }}({{t}_{2}}+\tau ,{{t}_{2}}){{\text{e}}^{\text{j}{{t}_{2}}\tau \cot \alpha }} \right\rangle }_{{{t}_{2}}}} \end{align}$ | (5) |
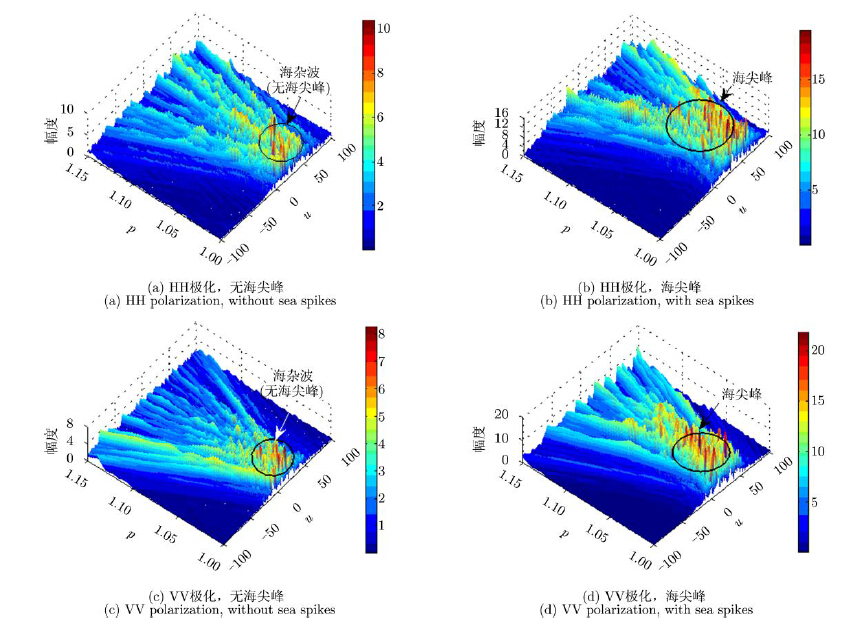
图 6比较了两种极化方式下海杂波背景和海尖峰的分数阶功率谱,可以得到以下几个结论:(1)由于FRFT对时频轴的旋转,增加的p轴能够获得海杂波多普勒的变化信息,更有利于分析时变的海尖峰信号,这一特性也可以从图 6(b)和图 6(d)中得出;(2)HH极化方式下,海尖峰的分数阶功率谱谱峰数量多于VV极化,说明VV极化的海尖峰频率变化不明显;(3)在高海况条件下,HH极化的海杂波背景功率水平高于VV极化,而后者海尖峰的功率水平却高于前者。
|
图 6 海杂波分数阶功率谱(IPIX-17#,N=512) Fig.6 FRFT spectrum of sea clutter (IPIX-17#,N=512) |
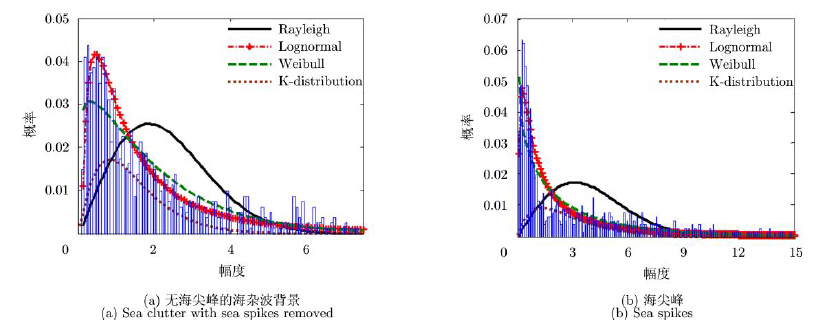
以上的结论与时域海杂波特性分析相一致。同样采用4种分布方式对海杂波的FRFT幅值进行幅度拟合分析,如图 7所示,却得到了与图 2(时域)截然相反的结论,海尖峰的FRFT幅值概率密度分布更为集中,“拖尾”减少,这是由于FRFT增加的p轴能够很好地反映频率的变化,使得具有时变特性的海尖峰能量分布集中。以上分析结果说明海尖峰具有非高斯、非平稳和高幅值等特点,从而不利于海杂波中目标的检测。
|
图 7 海杂波FRFT域幅度分布(IPIX-17#,HH极化) Fig.7 Amplitude distribution of sea clutter in FRFT domain (IPIX-17#,HH polarization) |
由海尖峰判别和特性分析结果可知,高幅值和时变特性使得海尖峰与海面动目标回波信号同样具有相似的特性,因此,需要设计相应的海尖峰抑制方法,提高回波信号的SCR。基于海尖峰判别和筛选的海杂波抑制方法通过剔除背景中的海尖峰并选取最小平均功率水平的背景杂波作为待检测数据,能够显著改善SCR,提高检测性能。根据式(1)的判定参数从海杂波序列中提取出海尖峰,此时,海杂波序列被分为无海尖峰的海杂波背景和海尖峰序列。将海尖峰序列置零,仅保留不含海尖峰的海杂波背景序列,分别计算各个海杂波背景序列的平均功率水平,假设海杂波序列被分为2n个数据段,其中第1,3,5,$\cdots $,2n-1段为海尖峰序列,而其余的第2,4,6,$\cdots $,2n段为海杂波背景序列,选取最小平均功率对应的海杂波背景序列作为待检测数据,计算方法为:
| $\begin{align} & {{i}_{0}}=\underset{i}{\mathop{\arg \min }}\,\left( \frac{1}{{{M}_{i}}}\sum\limits_{j=1}^{{{M}_{i}}}{{{\left| {{x}_{i}}(j) \right|}^{2}}} \right),\ \\ & \qquad \qquad i=1,\ 2,\ \cdots ,\ n,\ j=1,\ 2,\cdots ,\ {{M}_{i}} \\ \end{align}$ | (6) |
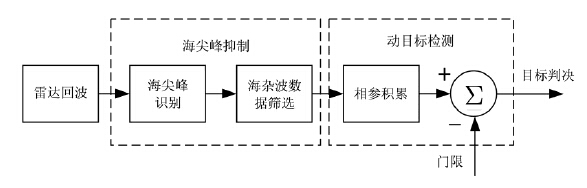
图 8给出了基于海尖峰判别和筛选的海杂波抑制及动目标检测方法。由于筛选出的海杂波背景序列大大降低了海尖峰的比重,可进一步改善SCR,达到抑制海杂波的目的,有助于后续的动目标信号检测。需要说明的是,待检测数据的筛选并不影响目标回波检测,当待检测单元为海杂波单元时,能量难以相参积累,其输出不能超过自适应门限;而当待检测单元为目标单元时,经海杂波数据筛选有可能会损失一部分目标能量,但由于抑制了海尖峰,SCR仍可在一定程度上得以改善。此外,后续的相参积累方法主要针对动目标运动特性设计,能够最大程度地匹配目标能量,而海杂波由于模型适配导致其能量难以积累,因此,仍能正确检测出目标,如针对匀速运动目标,可采用传统的动目标检测(Moving Target Detection,MTD)方法,针对匀加速目标,可采用FRFT等带有积累加速度分量的广义多普勒滤波器组方法[2, 17, 18]等。
|
图 8 海杂波抑制及动目标检测系统框图 Fig.8 Flowchart of sea clutter suppression and moving target detection |
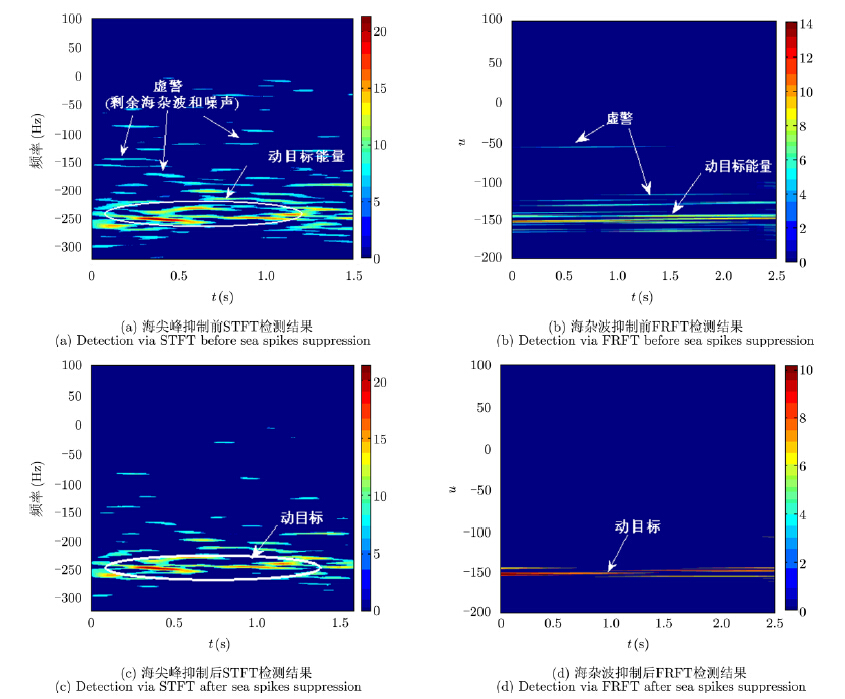
基于S波段对海观测雷达数据,进一步验证本文算法在实际雷达中的性能,如图 9和图 10所示。该组数据为顺风观测,显著波高为1.2 m,约为3级海况。低掠射角条件下,雷达观测距离范围为66 nm至75 nm,通过回波信号的距离-多普勒谱(图 9(a)),可以发现在73 nm附近存在一远离雷达运动的微弱目标,其多普勒频率分布不集中,频谱展宽。一方面说明目标作非匀速运动;另一方面则说明SCR较低,背景杂波干扰严重。图 9(b)给出了海尖峰的判别结果,由于观测距离较远,导致海杂波与大气噪声的功率水平相当,海杂波的分布类型更趋向于高斯分布。因此,海尖峰和背景杂波无明显区别。采用双参数恒虚警(Constant False Alarm Rate,CFAR)[19]检测,在${{P}_{\text{fa}}}\text{=1}{{\text{0}}^{-\text{4}}}$条件下,比较海尖峰抑制前后基于STFT和FRFT的动目标检测结果(图 10),可以发现,目标在STFT域能量主要集中在-250 Hz附近,但仍有大量的剩余海杂波和噪声,目标检测比较困难。采用本文提出的海杂波抑制方法后,海杂波得到明显抑制,大大提高了系统的检测性能。同时,由于目标的非匀速运动,采用FRFT更有利于积累目标能量,改善SCR。

|
图 9 雷达回波时频分析 Fig.9 Time-frequency analysis radar returns |
|
图 10 海面动目标检测结果(${{P}_{\text{fa}}}\text{=1}{{\text{0}}^{-\text{4}}},$ N=1024) Fig.10 Detection results of sea surface moving target (${{P}_{\text{fa}}}\text{=1}{{\text{0}}^{-\text{4}}},$ N=1024) |
本文对海杂波中非Bragg散射分量的典型(海尖峰)特性进行了研究,在海尖峰判别和筛选的基础上,分析其幅值特性、时间相关性、多普勒谱和分数阶功率谱特性,表明在高分辨率雷达,低擦地角、高海况以及HH极化工作方式下容易出现海尖峰,并且具有非高斯、长相关、非平稳和高幅值等特点。为此,提出一种海杂波抑制方法,该方法能够自适应抑制海杂波,改善SCR。实测数据验证表明,本文方法能够更好地抑制背景杂波和噪声,并能显著提高雷达对海面微弱目标的检测性能。
| [1] | Zuo L, Li M, Zhang X W, et al.. An efficient method for detecting slow-moving weak targets in sea clutter based on time-frequency iteration decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3659-3672.( 1) 1) |
| [2] | Chen X L, Guan J, Liu N B, et al.. Detection of a low observable sea-surface target with micromotion via the Radon-linear canonical transform[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(7): 1225-1229.( 1) 1) |
| [3] | Ward K D and Watts S. Use of sea clutter models in radar design and development[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 146-157.( 1) 1) |
| [4] | 闫亮, 孙培林, 易磊, 等. 基于逆高斯分布的复合高斯海杂波建模研究[J]. 雷达学报, 2013, 2(4): 461-465. Yan L, Sun P L, Yi L, et al.. Modeling of compound-Gaussian sea clutter based on an inverse Gaussian distribution[J]. Journal of Radars, 2013, 2(4): 461-465.(  1) 1) |
| [5] | Zhang M, Chen H, and Yin H C. Facet-based investigation on EM scattering from electrically large sea surface with two-scale profiles: theoretical model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 1967-1975.( 1) 1) |
| [6] | Greco M, Stinco P, and Gini F. Identification and analysis of sea radar clutter spikes[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 239-250.( 3) 3) |
| [7] | 陈小龙, 关键, 何友. 微多普勒理论在海面目标检测中的应用及展望[J]. 雷达学报, 2013, 2(1): 123-134. Chen X L, Guan J, and He Y. Applications and prospect of micro-motion theory in the detection of sea surface target[J]. Journal of Radars, 2013, 2(1): 123-134.(  2) 2) |
| [8] | Gutnik V G, Kulemin G P, and Sharapov L I. Spike statistics features of the radar sea clutter in the millimeter wave band at extremely small grazing angles[C]. The Fourth International Kharkov Symposium on Physics and Engineering of Millimeter and Sub-Millimeter Waves, Kharkov, Ukraine, 2001: 426-428.( 1) 1) |
| [9] | Posner F L. Spiky sea clutter at high range resolutions and very low grazing angles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 58-73.( 2) 2) |
| [10] | 梅孝安. IPIX雷达海尖峰统计特性研究[J]. 飞行器测控学报, 2007, 26(2): 19-23. Mei X A. A study on the statistical characteristics of IPIX radar sea spikes[J]. Journal of Spacecraft TT & C Technology, 2007, 26(2): 19-23.(  1) 1) |
| [11] | 谢常清, 杨俊岭. 雷达海杂波尖峰时频分布特性研究[J]. 现代雷达, 2008, 30(5): 10-13. Xie C Q and Yang J L. A study on the time-frequency distribution of radar sea clutter spike[J]. Modern Radar, 2008, 30(5): 10-13.(  1) 1) |
| [12] | Rosenberg L. Sea-spike detection in high grazing angle X-band sea-clutter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(8): 4556-4562.( 1) 1) |
| [13] | Tao R, Zhang F, and Wang Y. Fractional power spectrum[J]. IEEE Transactions on Signal Processing, 2008, 56(9): 4199-4206.( 2) 2) |
| [14] | Drosopoulos A. Description of the OHGR database[R]. Ottawa: DREO Technical Note, 1994.( 1) 1) |
| [15] | Dong Y and Merrett D. Analysis of L-band multi-channel sea clutter[J]. IET Radar, Sonar & Navigation, 2010, 4(2): 223-238.( 1) 1) |
| [16] | Walker D. Doppler modelling of radar sea clutter[J]. IEE Proceedings-Radar, Sonar and Navigation, 2001, 148(2): 73-80.( 1) 1) |
| [17] | Chen X L, Guan J, Huang Y, et al.. Maneuvering target detection via Radon-fractional Fourier transform-based long- time coherent integration[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 939-953.( 1) 1) |
| [18] | Chen X L, Guan J, Huang Y, et al.. Radon-linear canonical ambiguity function-based detection and estimation method for marine target with micromotion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2225-2240.( 1) 1) |
| [19] | Guida M, Longo M, and Lops M. Biparametric CFAR procedures for lognormal clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(3): 798-809.( 1) 1) |


