1 引言

海洋内波是发生在密度稳定层结的海水内部波动，在海洋内部，由于层结之间的密度差，致使很小的扰动就会在海洋内部产生轩然大波。内波是海洋中能量级串不可缺少的一环，在海洋的物质、动量和能量传输中扮演着重要角色，在整个海洋动力学的理论研究中占有重要地位。不仅如此，由于内波能在合成孔径雷达(Synthetic Aperture Radar,SAR)图像中观测到，证明内波的存在对海洋遥感，海面电磁散射系数的探测均有一定影响。同时海洋内波还与海洋声学、军事海洋学、海洋工程学等学科有着密切的联系，对水下航行、海洋观测也有显著影响。从上世纪70年代，人们开始用合成孔径雷达来观测海洋内波，人们发现，内波的存在会引起在SAR 图像上出现纹理变化。这使得内波对海洋电磁散射的影响的重要性日益凸显。

为了研究内波的SAR图像特征，很多针对内波的海洋遥感实验开始进行^{[1, 2, 3]}。依赖于这些实验数据和内波遥感资料。许多学者对内波成像机理进行了深入研究。Werner Alpers^[4]于1985年在Nature上发表论文，解释了内波的成像机理，由于内波在传播过程中引起了海洋内部流场的变化，进而调制表面毛细波，使得海表面的毛细波出现幅聚和幅散的效应。基于Bragg散射机制^[5]，海面的雷达散射系数也会发生变化，导致SAR图像上形成明暗相间的条纹。这一结论至今仍被相关领域的学者们广泛接受。

国家海洋局郑全安^[6]曾研究过内波的特征，这一研究从内波的KdV方程出发，基于谱平衡方程和Bragg散射理论，给出了内波存在的情况下，海面上雷达散射系数空间变化曲线，虽然这一研究主要仍是针对于内波参数的反演，但其中涉及到了内波对散射系数的影响分析。Brandt^[7]在这一工作的基础上，对电磁散射模型进行了改善，郑全安使用的Bragg散射模型认为海面只有一种尺度，即只存在能引起Bragg散射的海浪谐振波，而Brandt将双尺度模型引入内波散射计算中，认为海面上的Bragg毛细波被大尺度起伏的海浪调制，将海面大尺度海浪的波动考虑在内，使得模型更符合实际情况。中国海洋大学杜涛^[8]教授课题组基于郑全安的工作，系统研究了内波SAR图像成像过程，对于内波参数，雷达参数，海态参数对散射系数变化的影响做了较全面的分析。中科院Ouyang Yue^[9]博士同样分析了不同雷达频率，不同极化，不同入射角，不同风向角下内波对雷达散射系数的影响，旨在寻找探测内波所需的最佳雷达参数。以上所提到的所有研究都涉及到内波的存在对海面散射系数空间分布的影响，但其实研究的目的并不在于建立合理的散射模型，系统而全面地分析内波的散射特性。并且这些文献均没有建立时变的海面模型，也没有计算内波存在时，海面多普勒特性的变化。本文旨在从电磁散射的角度，研究内波对海面散射特性的影响，包括对散射系数和多普勒谱的影响。

2 理论模型 2.1 KdV方程

在流体力学中，内波的无方向性传播过程可以用KdV方程来描述^[10]

$\frac{{\partial \eta }}{{\partial t}} + ({C_0} + \alpha \eta + {\alpha _1}{\eta ^2})\frac{{\partial \eta }}{{\partial x}} + \beta \frac{{{\partial ^3}\eta }}{{\partial {x^3}}} = 0$

(1)

其中，η是内波垂直位移，t表示时间，x表示空间位置，C₀表示线性波波速。为简单，假定海水由二层水体构成，一层在跃层以上，称为上层(或混合层)，其深度为h₁，一层在跃层以下，称为下层(底层)，深度为h₂，海水总深度为h，且有h=h₁+h₂。在二层模式下，式(1)中的1阶非线性项α,2阶非线性项α₁及频散项β可分别表示为

$\alpha = \frac{{3{C_0}({h_1} - {h_2})}}{{2{h_1}{h_2}}} \hspace{115pt}$

(2)

${\alpha _1} = \frac{{3{C_0}}}{{h_1^2h_2^2}}\left[{\frac{7}{8}{{\left( {{h_2} - {h_1}} \right)}^2} - (h_2^2 - {h_1}{h_2} + h_1^2)} \right]$

(3)

$\beta = \frac{{{C_0}{h_1}{h_2}}}{6} \hspace{140pt}$

(4)

线性波波速C₀表示为：

${C_0} = \sqrt {\frac{{g\Delta \rho }}{\rho }\frac{{{h_1}{h_2}}}{{{h_1} + {h_2}}}}$

(5)

其中$\Delta \rho = {\rho _2} - {\rho _1}$ 为下层与上层海水的密度差，ρ是海水的平均密度。将式(2)～式(5)代入式(1)，并求解KdV方程，可得到稳定态的孤立波解^[8]

$ \eta (x,t) = \pm {\eta _0}{\rm{sec}}{{\rm{h}}^2}\left[{\frac{{x - C \,_0^\prime t}}{l}} \right]$

(6)

其中，η₀为内波最大振幅，通常内波的最大振幅从几米到几十米不等。当 ${h_1} < {h_2}$ 时，$\alpha < 0$ ，上式取负号，此时为下凹型内波；当 ${h_1} > {h_2}$ 时，$\alpha > 0$ ，上式取正号，此时为上凸型内波。 $C \,_0^\prime$ 为内波相速度，l为内波半波宽度，分别表示为：

$ C \,_0^\prime = {C_0} + \alpha {\eta _0}/3 = {C_0}\left[{1 + \frac{{{\eta _0}({h_2} - {h_1})}}{{2{h_2}{h_1}}}} \right] $

(7)

$l = \frac{{2{h_1}{h_2}}}{{\sqrt {3{\eta _0}\left| {{h_2} - {h_1}} \right|} }} \hspace{95pt}$

(8)

孤立内波的水粒子在上层海水中的速度可表示为：

${U_{\rm{x}}} = \frac{{{C_0}{\eta _0}}}{{{h_1}}}\sec \! {{\rm{h}}^{\rm{2}}}\left[{\frac{{{\rm{x - C}}_{\rm{0}}^\prime }}{{\rm{l}}}} \right]$

(9)

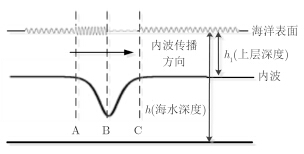
图 1以下凹型内波为例。给出了内波传播的示意图。本节给出的内波形态为孤立内波，即内波只存在一个大起伏。孤立内波通常也被称为孤立子。

2.2 内波对表面波高频谱的调制

对微波遥感所采用的P,L,C 和X波段有关的海面微尺度特征应当是那些具有若干分米，厘米，到若干毫米波长的海面超短波动。对于上述超短波，波动本身是小波陡的。因此波数空间中表面波谱的成长过程可以用波束谱平衡方程来描述

$\frac{{\partial \psi ({\bf{k}})}}{{\partial t}} + ({c_{\rm{g}}} + U)\nabla \psi ({\bf{k}}) \\ \qquad \; = {S_{{\rm{in}}}}({\bf{k}}) + {S_{{\rm{nl}}}}({\bf{k}}) + {S_{{\rm{ds}}}}({\bf{k}}) + {S_{{\rm{cu}}}}({\bf{k}})$

(10)

其中φ(k)表示海谱，k是海浪波数矢量，等式右边的4项分别表示风输入源函数，波-波相互作用源函数，耗散源函数和波-流相互作用源函数。在内波 研究中，内波对海表面频谱的影响主要体现在波-流 相互作用源函数上，其他源函数暂不考虑。只考虑波-流相互作用对频谱的调制，上式可简化为：

$\left[{\frac{\partial }{{\partial t}} + ({c_ \rm g} + U)\frac{\partial }{{\partial x}}} \right]\Delta \psi (k) = {S_\rm{cu}}(k)$

(11)

其中 $\Delta \psi (k)$ 为受内波影响，海表面波高频谱的变化值。根据文献^[6]，波-流相互作用可写为：

${S_{{\rm{cu}}}} = - \left( {{S_{{a b}}}\frac{{\partial {U_{b}}}}{{\partial {x_{a}}}}} \right)\psi (k)$

(12)

其中 ${U_{\beta}}$ 表示大尺度流场的速度分量，对于高频段海谱，海水可以认为是深水，上式中 $ {S_{\alpha \beta }}\frac{{\partial {U_\beta }}}{{\partial {\chi _\alpha }}} $ 可以写为：

$\begin{aligned} {S_{\alpha \beta }}\frac{{\partial {U_\beta }}}{{\partial {\chi _\alpha }}} = \left[{\frac{{\partial u}}{{\partial x}}{{\cos }^2}\varphi + \frac{{\partial v}}{{\partial y}}{{\sin }^2}\varphi } \right. \qquad \qquad \\ \left. { + \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)\cos \varphi \sin \varphi } \right]{\Big/}2 \end{aligned}$

(13)

将式(9)代入上式，可得

${S_{\alpha \beta }}{{\partial {U_\beta }} \over {\partial {\chi _\alpha }}} = - \left( {{{Co{{\cos }^2}\varphi } \over {h1l}}} \right){\eta _0} \\ \qquad \qquad \,\, \cdot \sec {h^2}\left( {{{\chi - {C^\prime }{o^t}} \over l}} \right)th\left( {{{\chi - {C^\prime }{o^t}} \over l}} \right)$

(14)

根据文献^[6]，将式(14)代入式(11)中，可以得到，内波的波-流相互作用对海谱产生的调制量为：

$\Delta \psi \left( k \right) = - m3{\omega ^{ - 1}}{k^{ - 4}}{\eta _0}\left( {{{Co{{\cos }^2}\varphi } \over {h1l}}} \right) \\ \qquad \qquad \,\, \cdot \sec {h^2}\left( {{{\chi - {C^\prime }{o^t}} \over l}} \right)th\left( {{{\chi - {C^\prime }{o^t}} \over l}} \right)$

(15)

2.3 电磁散射模型 2.3.1 电磁散射场计算

在本文中，我们采用复合表面模型来近似代替实际海洋表面，这种复合表面模型通常也称为双尺度模型^[11]。根据双尺度理论，单个面元的散射场可以表示为：

${\bf{E}}_{{\rm{pq}}}^{{\rm{scatt}}}{\rm{(}}{{\bf{\hat k}}_{\rm{i}}}{\rm{,}}{{\bf{\hat k}}_{\rm{s}}}{\rm{)}} = 2\pi \frac{{{{\rm{e}} {ik{R_0}}}}}{{i{R_0}}}{S_{{\rm{pq}}}}{\rm{(}}{{\bf{\hat k}}_{\rm{i}}}{\rm{,}}{{\bf{\hat k}}_{\rm{s}}}{\rm{)}}$

(16)

其中，${\bf{\hat k}}_{\rm{i}}$ 表示入射波矢量，${\bf{\hat k}}_{\rm{s}}$ 表示散射波矢量，下标p=h,v表示散射波的极化方式(h表示水平极化，v表示垂直极化)，q表示入射波的极化方式，R₀为雷达到散射中心的距离，S_pq为散射振幅，可以表示为：

${S_{{\rm{pq}}}}({{\bf{k}}_{\rm{i}}},{{\bf{k}}_{\rm{s}}}) = \frac{{{k^2}(1 - e )}}{{8{\pi ^2}}}{F_{{\rm{pq}}}}\iint\limits_{\Delta s} {\zeta ({\bf{r}}) {\rm e^{ - i({{\bf{k}}_{\rm{s}}} - {{\bf{k}}_{\rm{i}}}) \cdot {\bf{r}}}}{\rm{d}}{\bf{r}}} $

(17)

其中，F_pq为极化因子，可表示为：

${F_{{\rm{vv}}}} = \frac{1}{\varepsilon }[1 + {R_{\rm{v}}}({\theta _{\rm{i}}})][1 + {R_{\rm{v}}}({\theta _{\rm{s}}})]\sin {\theta _{\rm{i}}}\sin {\theta _{\rm{s}}}\\ \quad \quad \quad - [1 - {R_{\rm{v}}}({\theta _{\rm{i}}})][1 - {R_{\rm{v}}}({\theta _{\rm{s}}})]\cos {\theta _{\rm{i}}}\cos {\theta _{\rm{s}}}\cos {\phi _{\rm{s}}}$

(18)

${F_{{\rm{vh}}}} = [1 - {R_{\rm{v}}}(\theta _{\rm{i}}^{})][1 + {R_{\rm{h}}}(\theta _{\rm{s}}^{})]\cos \theta _{\rm{i}}^{}\sin \phi _{\rm{s}} \hspace{35pt}$

(19)

${F_{{\rm{hv}}}} = [1 + {R_{\rm{h}}}(\theta _{\rm{i}}^{})][1 - {R_{\rm{v}}}(\theta _{\rm{s}}^{})]\cos \theta _{\rm{s}}^{}\sin \phi _{\rm{s}} \hspace{35pt}$

(20)

${F_{{\rm{hh}}}} = [1 + {R_{\rm{h}}}(\theta _{\rm{i}}^{})][1 + {R_{\rm{h}}}(\theta _{\rm{s}}^{})]\cos \phi _{\rm{s}} \hspace{60pt}$

(21)

其中，R_h,R_v分别为水平极化和垂直极化下的菲涅尔反射系数，θ_i,θ_s分别为入射波在每个面元上的局部入射角和反射角，ø_s为局部散射角的方位角，ε为海水的介电常数。需要注意的是，以上两式均是局部坐标下的表达式，在具体计算时，需要将散射结果转化至全局坐标系下，限于篇幅，具体转化过程在本文中不再给出。

式(17)中的对微表面积分的部分可以表示为I(·)，即

$\begin{aligned} I( \cdot ) = \iint\limits_{\Delta s} {\zeta (r){{\rm{e}}^{ - i({k_{\rm{s}}} - {k_{\rm{i}}}) \cdot r}}} {\rm{d}}{\bf{r}} \qquad \qquad \qquad \quad \; \\ {\rm{ = }}\frac{1}{n_{z}}\int_{ - \Delta {x_{\rm{g}}}/2}^{\Delta {x_{\rm{g}}}/2} {} \int_{ - \Delta {y_{\rm{g}}}/2}^{\Delta {y_{\rm{g}}}/2} {\zeta r{{\rm{e}} ^{ - i({{\bf{R}}_{\rm{s}}} - {{\bf{R}}_{\rm{i}}}) \cdot {r}}} {\rm{d}}x{\rm{d}}y} \end{aligned}$

(22)

其中ζ(r)表示面元上的小尺度毛细波起伏，其中r为面元上点的位置。在复合表面模型中，ζ(r)通常认为其是一列能引起入射电磁波Bragg谐振的正弦波。

$\zeta ({\bf{r}}) = B({{\bf{k}}_{\rm{c}}})\sin ({\bf{k}} \cdot {\bf{r}} - {\omega _{\rm{c}}}t)$

(23)

其中，$B({{\bf{k}}_{\rm{c}}}) = \sqrt {\psi \left( {{{\bf{k}}_{\rm{c}}}} \right)/\Delta S}$ 表示面元上正弦毛细波的振幅。由于式(23)可以表示为指数函数的叠加，将式(23)代入式(22)中，通过球贝塞尔函数展开之后可得到I(·)的解析表达式^[12]

$I\left( \cdot \right)\! = \!\frac{{B({{\bf{k}}_{\rm{c}}})}}{{2{n_z}}}{{\rm{e}}^{ - i{\bf{q}} \cdot {{\bf{r}}_0}}}\sum\limits_{n = - \infty }^\infty {{{( - i)}^n}} {J_{\rm{n}}}[{q_z}B({{\bf{k}}_c})]\mathop \smallint \nolimits_{ - \Delta {x_{\rm{g}}}/2}^{\Delta {x_{\rm{g}}}/2} \int_{ - \Delta {y_{\rm{g}}}/2}^{\Delta {y_{\rm{g}}}/2} \\ \qquad \quad {\left\{ {{{\rm{e}}^{i\left\{ {\left[ {(1 + n){k_{{\rm{c}}x}} - {q_x} - {q_z}{Z_x}} \right]{x_c} + \left[ {(1 + n){k_{{\rm{c}}y}} - {q_y} - {q_z}{Z_y}} \right]{y_{\rm{c}}}} \right\}}}} \right.} \\ \qquad \quad \cdot {{\rm{e}}^{ - i(1 + n){\omega _{\rm{c}}}t}} + \left. {{{\rm{e}}^{ - i\left\{ {\left[ {(1 - n){k_{{\rm{c}}x}} + {q_x} + {q_z}{Z_x}} \right]{x_{\rm{c}}} + \left[ {(1 - n){k_{{\rm{c}}y}} + {q_y} + {q_z}{Z_y}} \right]{y_{\rm{c}}}} \right\}}}{{\rm{e}}^{i(1 - n){\omega _{\rm{c}}}t}}} \right\}{\rm{d}}{x_{\rm{c}}}{\rm{d}}{y_{\rm{c}}}$

(24)

其中，Z_x为面元沿x方向的斜率，Z_y为面元沿y方向的斜率。将式(24)，式(17)代入式(16)中，即可得到每个面元的散射场，而整个海面的散射总场即可表示为：

$E_{{\rm{pq}}}^{{\rm{total {\tiny\_} scatt}}}{\rm{(}}{{\bf{\hat k}}_{\rm{i}}}{\rm{,}}{{\bf{\hat k}}_{\rm{s}}}{\rm{)}} = \sum\limits_{}^M {\sum\limits_{}^N {{\bf{E}}_{{\rm{pq}}}^{{\rm{scatt}}}} } $

(25)

其中，M表示x方向的面元个数，N表示y方向的面元个数。经过以上推导，可以得到内波存在下海面的回波场。 2.3.2 电磁散射系数计算

对于一个小面元，散射系数可表示为：

$\sigma _{{\rm{pq}}}^0{\rm{(}}{{\bf{\hat k}}_{\rm{i}}}{\rm{,}}{{\bf{\hat k}}_{\rm{s}}}{\rm{)}}\! =\! 4\pi R_0^2\left\langle {{\bf{E}}_{{\rm{pq}}}^{{\rm{scatt}}}{\rm{(}}{{{\bf{\hat k}}}_{\rm{i}}}{\rm{,}}{{{\bf{\hat k}}}_{\rm{s}}}{\rm{)}}{{\left[{{\bf{E}}_{{\rm{pq}}}^{{\rm{scatt}}}{\rm{(}}{{{\bf{\hat k}}}_{\rm{i}}}{\rm{,}}{{{\bf{\hat k}}}_{\rm{s}}}{\rm{)}}} \right]}^*}} \right\rangle \!{\Big/}\!\Delta S$

(26)

将式(16)、式(17)代入上式，可得

$\eqalign{ \sigma _{{\rm{pq}}}^0({{{\bf{\hat k}}}_{\rm{i}}},{{{\bf{\hat k}}}_{\rm{s}}}) = \pi {k^4}{\left| {\varepsilon - 1} \right|^2}{\left| {{F_{{\rm{pq}}}}} \right|^2}{1 \over {{{\left( {2\pi } \right)}^2}}} \qquad \,\,\,\,\, \\ \qquad \qquad \qquad \,\, \cdot \int\!\!\!\int {\left\langle {\zeta ({r^\prime })\zeta (r)} \right\rangle {{\rm{e}}^{ - iq \cdot ({{\bf{r}}^\prime } - {\bf{r}})}}{\rm{d}}{{\bf{r}}^\prime }{\rm{d}}{\bf{r}}} \cr}$

(27)

上式右边的积分部分与前面的系数一起，正好是海谱的定义，可表示为：

$\psi ({\bf{k}}) = \frac{1}{{{{\left( {2\pi } \right)}^2}}}\iint {\left\langle {\zeta ({{\bf{r}}^\prime})\zeta ({\bf{r}})} \right\rangle } {{\mathop{\rm e}\nolimits} ^{ - i2k({{{\bf{\hat k}}}_{\rm{s}}} - {{{\bf{\hat k}}}_{\rm{i}}}) \cdot ({{\bf{r}}^\prime} - {\bf{r}})}}{\rm{d}}{{\bf{r}}^\prime}{\rm{d}}{\bf{r}}$

(28)

每个面元的散射系数进而可以表示为：

$\sigma _{{\rm{pq}}}^0{\rm{(}}{{\bf{\hat k}}_{\rm{i}}}{\rm{,}}{{\bf{\hat k}}_{\rm{s}}}{\rm{)}} = \pi {k^4}{\left| {\varepsilon - 1} \right|^2}{\left| {{F_{{\rm{pq}}}}} \right|^2}\psi \left( {{{\bf{q}}_{\rm{1}}}} \right)$

(29)

Ψ(q₁)是表面毛细波的海谱，q₁是散射矢量 ${\bf{q}} = k({{\bf{\hat k}}_{\rm{s}}} - {{\bf{\hat k}}_{\rm{i}}})$ 在倾斜面元上的投影。在内波存在的情况下Ψ不再是传统计算海面的谱值，需要进行调制 $\psi = {\psi _{{\rm{sea}}}} + \Delta \psi $ ，而 $\Delta \psi $ 即为2.2节中得到的海面高频谱调制值。

2.3.3 多普勒谱计算

动态海面下，海表面轮廓随着时间不段发生变化，对于风趋海面，海面朝着风向方向运动。根据式(29)，容易得到一组对应不同时刻海面样本的电磁散射场时间序列，这样时变海面多普勒谱即可通过标准谱估计方法获得，公式 如下：

$S(f) = \frac{1}{T}{\left| {\int\nolimits_0^T {{\bf{{\rm E}}}_{{\rm{pq}}}^{{\rm{total {\tiny\_} scatt}}}{\rm{(}}{{{\bf{\hat k}}}_{\rm{i}}}{\rm{,}}{{{\bf{\hat k}}}_{\rm{s}}}{\rm{,}}t{\rm{)exp(}}i2\pi ft{\rm{)}}{\rm{d}}t} } \right|^2}$

(30)

其中，T为观测时间，dt为时间采样间隔，f为多普勒频率，单位通常为赫兹(Hz)。具有统计意义的多普勒谱通常需要对多组动态海面样本取平均后才能得到，即：计算完一组动态海面的时间序列；由式(30)计算该组时间序列的多普勒谱；变换不同的动态海面样本，重复以上两步，假设重复计算了N_s组时变海面样本，那么，对N_s组谱估计结果求平均，即可得到平均多普勒谱线。

3 数值结果和分析 3.1 内波对散射系数的影响

在计算内波海面电磁散射时，我们首先生成海面的大尺度起伏，并将海面离散为M×N个面元；计算每个面元的散射系数，如果这一面元在某一时刻内下部有内波存在，在计算该面元散射时考虑内波对面元上毛细波粗糙度的修正。图 1首先对比了内波存在和不存在时海面散射系数分布。计算参数如下：入射波频率为 $f = 8.0 \ {\rm{GHz}}$ ，入射角为 ${\theta _{\rm{i}}} = {45^\circ}$ ，入射方位角为 ${\varphi _{\rm{i}}} = {0^\circ}$ ，海面上10 m处风速为U=2.2 m/s，根据Debye模型，计算得到的海水介电常数为 $\varepsilon = (61.18,35.85)$ ，所计算海面的尺寸为1024 m × 512 m，上层深度为h₁=15 m，下层深度为h₂=45 m，内波最大振幅为η₀=10 m ，上下层的归一化海水密度差为Δρ/ρ= 1.5 × 10² 。由于2.1节中给出的内波轮廓是无方向性的，为了在散射系数分布图中直观体现出内波的影响，假设内波沿着x轴传播，且将内波沿着y轴进行延拓。需要说明的是，文中所给出的内波几何轮廓模型只是一种常用的经典模型。事实上，很多学者根据测量生成的SAR图像，从理论上给出了多种内波模型。如在文献^{[13, 14, 15]}中，有些模型给出了若干列内波同时存在，甚至产生交汇的内波传播模型，以及内波传播中经过岛屿后形态的变化的传播模型。而在本文中，由于重点在于研究内波存在对散射系数的影响，而不在于从流体力学或者海洋动力学方面研究内波传播特性，所以我们采用了比较简单的内波传播模型。

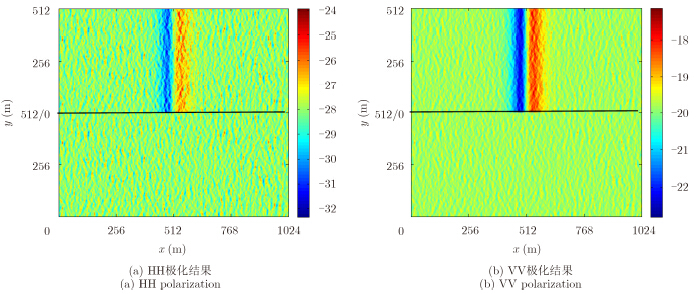
图 2给出了海面以下存在内波和不存在内波两种情况下的海面电磁散射系数分布图。散射系数取dB。图 2(a)为HH极化下结果，图 2(b)为VV极化下结果。其中图的下半部分为没有内波存在时海面电磁散射系数分布，从散射系数分布可以体现出海面的大尺度海浪起伏。而有内波存在时，由于内波对表面波的调制，在内波幅度的不断减小时，表面波产生幅散现象(如图 1中AB段所示)，导致表面波粗糙度减小，根据Bragg散射理论，粗糙度减小会引起散射系数变小；相应的内波振幅增加时，毛细波产生幅聚现象(如图 1中BC段所示)，粗糙度增大，散射系数会增大，使得海表面出现亮暗变化的条纹。由于本文中模拟的是下凹型内波，所以散射系数先变小后变大，条纹为暗亮相间。

为了研究内波对散射系数的影响，我们定义 $\Delta \sigma $ 表示散射系数的变化，$\Delta \sigma $ 表示为：

$\Delta \sigma = \sigma - {\sigma ^0}$

(31)

其中$\sigma $为内波存在时每个面元的散射系数，$\sigma $⁰表示没有内波时海面本身的散射系数。 $\Delta \sigma $ 也被称为内波的调制深度。图 3中给出了不同参数下 $\Delta \sigma $ 随空间位置变化规律。为了更为直观地体现各种不同参数下散射系数变化规律，以下只给出散射系数差值沿x轴的变化。图中均只给出了水平极化(即HH极化)下的结果，VV结果与HH结果得到的规律类似，限于篇幅，本文不再给出VV极化下 $\Delta \sigma $ 随不同参数的变化规律。需要说明的是，由于本文采用的是复合表面模型，即考虑了大尺度波对散射系数的调制作用，故图 3中 $\Delta \sigma $ 随空间位置变化的曲线并不平滑，因为大尺度的起伏会使得散射系数产生波动。图 3中的参数都在图中给出，在这里不一一 列出。

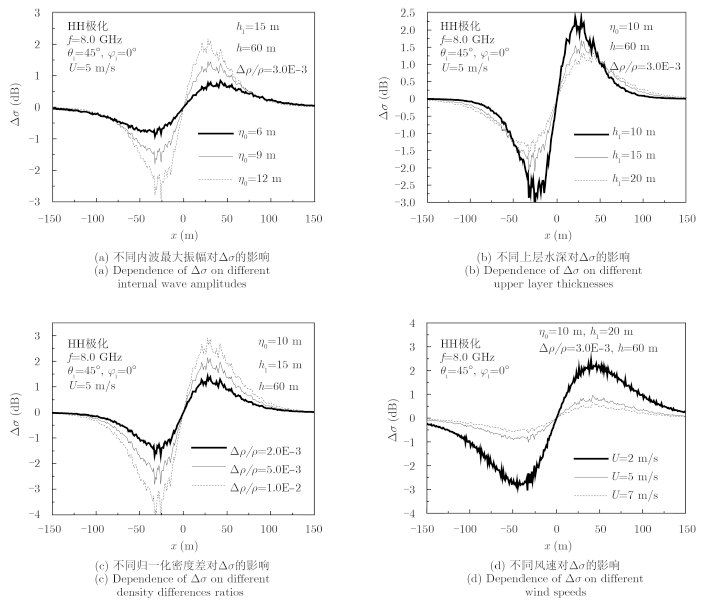
图 3(a)给出了不同内波振幅对散射系数的影响。可以看到，随着内波最大振幅的增加，调制深度 $\Delta \sigma $ 的变化越大，内波调制作用越明显。这是因为内波振幅越大，证明内波越剧烈，对海洋表面毛细波影响越大。从散射系数上，更易观察到内波的存在。图 3(b)为不同上层水深对 $\Delta \sigma $ 的影响，水深越浅，散射系数差的起伏越明显。可以推测，在SAR图像中，明暗条纹会愈加明显。上层水深较浅的情况下，内波起伏引起的海洋内部扰动更容易通过波流相互作用传播至海洋表面，使得幅聚幅散效应更加明显。不同归一化密度对 $\Delta \sigma $ 的影响在图 3(c) 中给出。显然，上下层之间的密度差越大，$\Delta \sigma $ 起伏变化越明显，这是由于内波本身就是由上下层之间存在密度差，一旦产生微小扰动，这一密度差就会使得扰动不断增大，打破海水的稳态状态，内波得以产生，故密度差越大，内波将会越剧烈，会更大程度地调制表面毛细波，引起散射系数更剧烈的变化。图 3(d)为不同风速下的模拟结果，可以看出，风速越大，内波引起的散射系数变化越不明显，因为随着风速的增加，海面更加粗糙，杂波更加剧烈，内波仅对表面微小起伏存在调制，而这种调制在大风速下容易被淹没。

3.2 内波对多普勒谱的影响

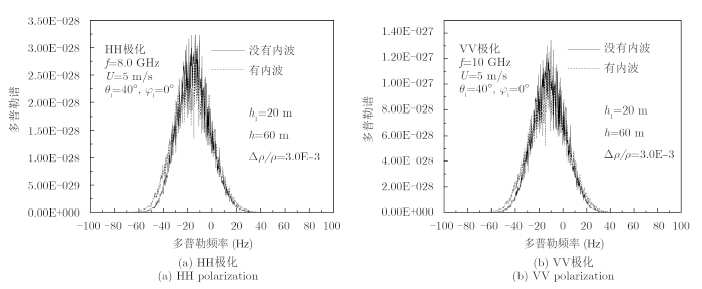
下面我们将数值模拟并分析内波对海面多普勒谱的影响。图 4给出了有无内波情况下海面的多普勒谱。动态海面生成的的时间间隔为 $ \Delta t$ = 0.005 s，时间采样点为1024，总的观测时间为T=5.12 s。一共取50组动态海面样本进行集平均，计算动态海面多普勒谱。

从图 4可以看出，对比没有内波的情况，有内波的情况下，多普勒谱会在峰值附近有所下降，而在非峰值部分谱值有所上升，对应的，多普勒谱产生了一定的展宽。为了解释这一现象，我们假设原来能引起海面Bragg散射的毛细波成分波数为k。根据内波对毛细波调制的原理可知：由于内波的存在，表面毛细波受到了调制，一部分产生幅聚，体现在粗糙度变大，毛细波的波数就会相应变大；相反，产生幅散效应的毛细波波数会相应变大。不同的波数对应不同的波传播速度，而不同的传播速度就会体现在多普勒谱上，对应不同的多普勒频率，因此使得峰值多普勒频率对应的谱下降，而其他区域谱值变大。

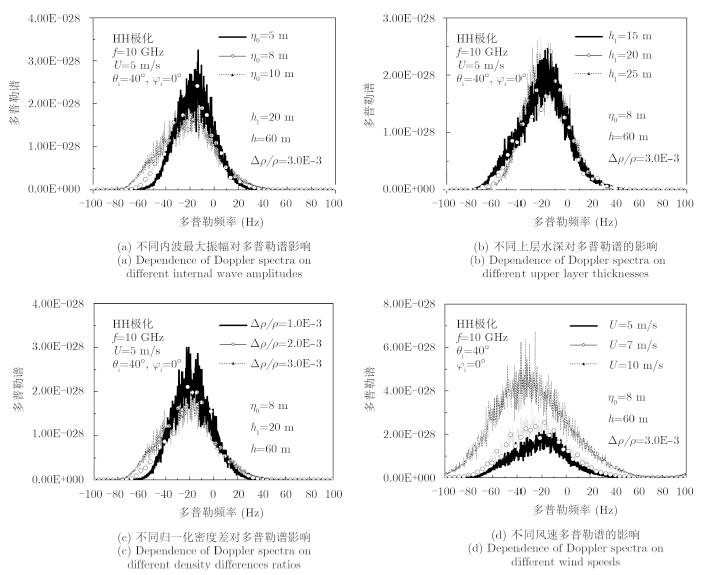
图 5给出了不同参数的变化对多普勒谱的影响。从图 5(a)中可以看出，随着内波振幅的增大，多普勒谱的变化模式和图 4中一致，即峰值频率对应值减小，其他频率对应值增大。内波振幅越大，这种影响越明显。图 5(b)显示了不同上层深度对多普勒谱的影响，上层深度越浅，内波对多普勒谱影响越明显。同时海水上下层密度差越大，内波对多普勒影响越明显(如图 5(c)所示)。图 5(f)表明，随着风速的增大，频移变大，多普勒频谱变宽，可以看到，多普勒谱随海态条件的变化与没有内波的海面多普勒变化规律相同。由此可见，内波的存在只是影响了多普勒谱的值和宽度，并没有影响海面回波多普勒谱随风速的变化规律。

4 结束语

本文研究了海洋内部有内波存在时海面的散射特性，基于KdV方程建立孤立内波模型，考虑波-流相互作用，对毛细波进行调制，最后利用复合表面模型，计算了内波存在和不存在时海面的散射系数变化，以及动态海面的多普勒谱。计算结果显示，内波会使得海面散射系数出现波动起伏，体现为暗亮相间的条纹。内波存在的情况下，会使得回波的多普勒谱中间降低，两边升高，造成频谱变宽的现象。