② 中国航天科工二院 北京 100854)
③ 中国传媒大学信息工程学院 北京 100024)
② The Second Academy of China Aerospace Science and Industry Corporation, Beijing 100854, China
③ Information Engineering School, Communication University of China, Beijing 100024, China
多层介质结构(如建筑物、雷达天线罩、地表面等)作为一种常用结构形式,广泛存在于各类人造目标、自然环境,其电磁散射特性建模在穿墙雷达探测、天线罩设计、合成孔径雷达(Synthetic Aperture Radar,SAR)仿真、多层介质目标特征建库、目标与环境一体化建模等方面具有重要的应用价值[1, 2, 3, 4, 5, 6, 7]。然而,尽管计算电磁学理论和计算机技术取得了长足发展,但电大尺寸多层介质目标电磁散射建模效率依然难以满足实际应用的要求,因此迫切需要寻求一种更加高效的工程建模途径。
多层介质结构由若干厚度不同的均匀介质层组成,其电磁散射建模过程远比理想导体目标复杂。经典的解析方法只能解决有限几种典型形体多层介质的散射问题,如平面形体、柱体和球体[8]。针对复杂形体多层介质结构,主要采用数值方法和高频渐近方法。前者基于电磁场微分或积分方程,包括时域有限差分法(Finite Difference Time Domain, FDTD)、矩量法(Method of Moment,MoM)、多层快速多极子算法(Multilevel Fast Multipole Algorithm,MLFMA)等[9, 10, 11, 12, 13],具有计算精度高、适应性强的优点,但计算时间过长,对计算机硬件要求很高,难以满足工程应用的时效需求。后者从散射机理出发,以光学射线追踪为基础[14, 15, 16],结合几何光学法(Geometrical Optics,GO)、物理光学法(Physical Optics,PO)和一致性绕射理论(Uniform Theory of Diffraction,UTD)等[3, 17],实现对多层介质结构电磁散射特性的快速计算。高频渐近方法虽计算精度不如数值方法,但计算效率高,资源需求少,工程实用性强。
目前,基于射线追踪的高频渐近方法已在多层介质结构散射和辐射问题中得到应用[3, 17, 18, 19, 20, 21]。随着目标电尺寸不断增大,高频渐近方法对计算资源和时间的需求迅速增长,主要表现为:初始射线数巨大,且射线数随追踪深度(射线弹跳次数)指数增长。针对上述计算资源和效率瓶颈问题,本文在射线追踪方法基础上,采用传输线等效理论对多层介质目标模型进行等效处理[21, 22, 23],极大地降低射线追踪复杂度。传输线等效模型采用电路分析中网络分析方法计算多层介质的反射/透射系数,只关心多层介质结构总体影响,无需具体计算射线在多层介质内部的多次反射与折射。然而,传输线等效模型在实际建模中面临以下两个问题:一是利用传输线理论计算透射系数时,仅考虑了电磁波在多层介质中的纵向传输相位延迟,忽略了横向传输相位延迟,当多层介质厚度较大或电磁波入射角较大时,电磁波横向传输相位延迟对散射场影响明显[21]。二是传输线等效模型与射线追踪难以有效结合,针对多层介质结构构成的复杂模型,多层介质结构的传输线等效模型中,透射射线透射位置为入射射线入射位置的纵向平移,而射线追踪则是根据Snell定律[24]计算透射射线方向,并结合几何模型计算透射射线的透射位置。这严重制约了传输线等效模型在超电大复杂多层介质结构目标电磁散射特性分析中的应用。
针对上述问题,本文首先提出了多层介质结构基于传输线理论的等效面模型,将多层介质结构等效为平面,根据传输线理论计算该平面的反射/透射系数,根据Snell定律计算反射/透射方向。该方法不仅极大地降低了超电大复杂目标模型构建和射线追踪的复杂度,而且成功解决了传输线等效模型难以与射线追踪有效结合的问题。同时,由于等效面模型引入新的相位误差,本文推导了相应的相位修正算法,具体通过引入多层介质结构厚度、入射和观测方向等信息对反射/透射系数的相位进行修正。最后,通过对双层介质平板、建筑物等目标进行仿真计算,验证了本文方法的正确性和高效性。
2 传输线等效模型 2.1 传输线理论N层均匀介质平板及其传输线等效模型如图 1 所示。图中第m层介质板厚度为tm,相对介电常数和相对磁导率分别为em和mm,对应等效传输线长度为tm,等效传播常数为 $\beta _m^{{\rm{TL}}}$ ,等效波阻抗为 $Z_m^{{\rm{TL}}}$ 。
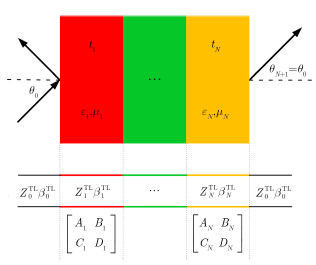
|
图 1 N 层介质平板及其传输线等效模型 Fig.1 N-layered slab and its transmission line equivalent model |
第m层均匀介质平板对应传输线的传输矩阵可表示为[21, 22, 23]:
| $\left[\!\!{\begin{array}{*{20}{c}} {{A_m}\ {B_m}}\\ {{C_m}\ {D_m}} \end{array}} \!\! \right] \\ \quad = \left [\!\! {\begin{array}{*{20}{c}} \ \ \ { \cosh ({\rm{j}}{\beta _m^{{\rm{TL}}}}{t_m}) \qquad \quad \; Z_m^{{\rm{TL}}}\sinh ({\rm{j}}{\beta _m^{{\rm{TL}}}}{t_m})} \\ \!\! { \sinh ({\rm{j}}{\beta _m^{{\rm{TL}}}}{t_m})/Z_m^{{\rm{TL}}} \qquad \quad \cosh ({\rm{j}}{\beta _m^{{\rm{TL}}}}{t_m}) } \end{array}} \!\! \right]$ | (1) |
| $\beta _m^{{\rm{TL}}} = {k_m}\cos {\theta _m} = {k_0}\sqrt {{\mu _m}{\varepsilon _m}} \cos {\theta _m} \hspace{12pt} \hspace{40pt}$ | (2) |
| $Z_m^{{\rm{TL}}} = \ \!\! \left\{ {\begin{array}{*{20}{l}} \!\! {{\eta _0}\sqrt {{\mu _m}/{\varepsilon _m}} \cos {\theta _m},\quad\ /\!/ }\\ {{\rm{ }} \!\! {\eta _0}\sqrt {{\mu _m}/{\varepsilon _m}} / \cos {\theta _m},\quad \bot } \end{array}} \!\! \right. \hspace{65pt}$ | (3) |
N层均匀介质平板的总传输矩阵可表示为:
| $\left[\!\! {\begin{array}{*{20}{c}} {{A} \quad {B}}\\ {{C} \quad {D}} \end{array}} \!\! \right] = \left[\!\! {\begin{array}{*{20}{c}} {{A_1} \quad {B_1}}\\ {{C_1} \quad {D_1}} \end{array}} \!\! \right]\left[\!\! {\begin{array}{*{20}{c}} {{A_2} \quad {B_2}}\\ {{C_2} \quad {D_2}} \end{array}} \!\! \right] \cdots \left[\!\! {\begin{array}{*{20}{c}} {{A_N} \quad {B_N}}\\ {{C_N} \quad {D_N}} \end{array}} \!\! \right]$ | (4) |
根据电路网络理论[22, 23],N层均匀介质平板的反射系数与透射系数可表示为:
| $R = \frac{{\left( {A + B/Z_{N + 1 \;\; }^{{\rm{TL \; }}}} \right) - Z_0^{{\rm{TL \; }}}\left( { C + D/Z_{N + 1 \;\; }^{{\rm{TL \; }}}} \right)}}{{\left( {A + B/Z_{N + 1 \;\; }^{{\rm{TL \; }}}} \right) + Z_0^{{\rm{TL \; }}}\left( {C + D/Z_{N + 1 \;\; }^{{\rm{TL \; }}}} \right)}}$ | (5) |
| $T = \frac{2}{{\left( {A + B/Z_{N + 1 \;\; }^{{\rm{TL \; }}}} \right) + Z_0^{{\rm{TL \; }}}\left( {C + D/Z_{N + 1 \;\; }^{{\rm{TL \; }}}} \right)}}$ | (6) |
将平行极化与垂直极化下的等效波阻抗分别代入式(1),式(4)-式(6),可计算得到两组极化下的反射系数与透射系数。
2.2 散射场计算在计算获得多层介质平板结构的反射系数与透射系数后,反射场Er与透射场Et可由入射场Ei分别求出。根据等效原理,任意用一个闭合面(Huygens面)S包围目标,闭合面S外散射场E,H由闭合面S上全部电磁场Es,Hs共同产生[24, 25]。
根据Stratton-Chu方程,闭合面S外任一点电磁场E,H可由闭合面上的场Es,Hs及自由空间Green函数 ${G_0}\left( {r,r'} \right)$ 表示为:
| ${E\left( r \right) = \oint_S {\left[{ - {\rm{j}}\omega \mu \left( {{e_{\rm{n}}} \times {H_{\rm{s}}}} \right) + \left( {{e_{\rm{n}}} \times {E_{\rm{s}}}} \right) \times \nabla '} \right.} }\\ \quad \qquad \ \; {\left. { + \left( {{e_{\rm{n}}} \cdot {E_{\rm{s}}}} \right)\nabla '} \right]{G_0}\left( {r,r'} \right){\rm{d}}S'} $ | (7) |
| ${H\left( r \right) = \oint_S {\left[{\rm j\omega \varepsilon \left( {{e_{\rm{n}}} \times {E_{\rm{s}}}} \right)+ \left( {{e_{\rm{n}}} \times {H_{\rm{s}}}} \right) \times \nabla '} \right.} }\\ \quad \qquad \ \; {\left. { + \left( {{e_{\rm{n}}} \cdot {H_{\rm{s}}}} \right)\nabla '} \right]{G_0}\left( {r,r'} \right){\rm{d}}S' \hspace{40pt}} $ | (8) |
| ${G_0}\left( {r,r'} \right) = \frac{{{{\rm{e}}^{ - {\rm{j}}k\left| {r - r'} \right|}}}}{{4π \left| {r - r'} \right|}}$ | (9) |
视具体情况而异,式(7),式(8)中Es,Hs一般取为Er,Hr或Et,Ht,最后通过口径积分计算多层介质结构的散射场。
3 等效面模型及其相位修正算法 3.1 等效面模型针对多层介质平板结构、曲率半径远大于波长的多层曲面介质结构、以及由其构成的复杂介质目标,如建筑物、雷达天线罩等,基于一定的准则将多层介质结构等效为平面或曲面,由等效后的平面或曲面构成的新模型即为等效面模型。
图 2所示为图 1中N层介质平板的等效面模型,等效面两侧均为自由空间,反射/透射角均与入射角相同,反射/透射系数根据传输线理论计算。等效面位置可任意选取,既可选择多层介质结构与自由空间的分界面,也可选择介质层内任意位置。为方便对复杂多层介质目标建模和推导统一的相位修正公式,选定多层介质结构对称中心面为等效面。
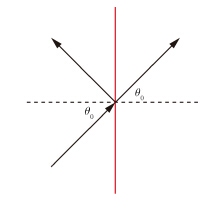
|
图 2 多层介质结构等效面模型 Fig.2 Equivalent plane model of multi-layered dielectric structure |
多层介质结构的等效面模型较实体模型具有以下显著优势:一是目标模型构建更为简单,图 3所示分别为简化后的四室建筑物实体模型和等效面模型,其中实体模型包含26个面,而等效面模型仅包含9个面。二是射线追踪过程复杂度更低,为仿真获取图 3建筑物模型的SAR图像,电磁波需穿透三面墙,共6个介质分界面,两组模型对应的射线追踪简化示意图如图 4所示,实体模型的最小追踪深度为11层,而等效面模型的最小追踪深度仅为5层。需要强调的是,射线追踪过程中入射射线会不断分裂为反射射线与折射射线,以一根射线为例,实体模型在最小射线追踪深度下最终射线数为442根,而等效面模型为11根,射线数降低为实体模型的2.49%,极大地简化了射线追踪过程,降低了射线追踪的时间和内存消耗。三是散射场计算更为快捷,射线数的急剧降低,直接减少了散射场计算的时间,显著提高了计算效率。
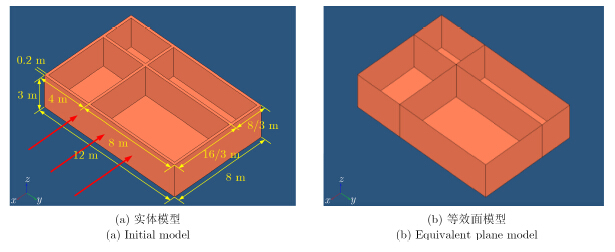
|
图 3 四室建筑物模型 Fig.3 The building model with 4 rooms |
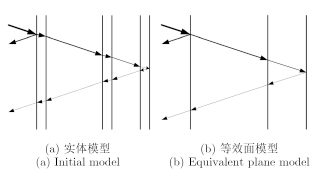
|
图 4 射线追踪示意图 Fig.4 The schematic diagram of ray tracing |
在构造完成等效面模型后,可以直接利用传统的射线追踪方法快速获取电磁波的传播路径,以及传播过程中场强与相位的变化。当然,该模型对复杂目标的计算精度存在一定影响,主要是因为等效面位置的选取会导致尺寸的微小偏差,如建筑物模型拐角处,但对整体仿真结果影响不大,具有很好的工程实用价值。
3.2 相位修正算法多层介质结构等效为平面后,厚度降为零,电磁波穿过原多层介质结构区域时变为在自由空间传播,但基于传输线理论计算的透射系数包含了电磁波穿过多层介质结构时的纵向分量相位延迟。因此,电磁波在原多层介质结构区域的自由空间传播引入了新的相位误差,下面将推导相位修正公式。
图 5所示为多层均匀介质平板传输线等效模型及其等效面模型(中间黄色线条),其中传输线等效模型的入射射线在P1点反射、在P2点透射,等效面模型的入射射线在Q点反射与透射。
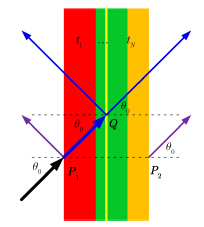
|
图 5 多层介质平板传输线等效模型及其等效面模型 Fig.5 Multi-layered dielectric slab’s transmission line equivalent model and equivalent plane model |
为修正电磁波在原多层介质结构区域的自由空间传播引入的新相位误差,需要对等效面模型的反射系数与透射系数进行相位修正,下面给出了相位修正公式(详细推导过程见附录)。
| ${R^m} = R{e^{{\rm{j}}{k_0}{P_1}Q \cdot \left( {\hat i - \hat s} \right)}}$ | (10) |
| ${T \;^m} = T\,{e^{{\rm{j}}{k_0}\left( {{ P_1} Q \cdot \hat i - { P_2} Q \cdot \hat s} \right)}} \hspace{33pt}$ | (11) |
| ${P_1}Q = 0.5{t_{{\rm{total}}}}{\rm{sec}}{\theta _0}\hat i \hspace{41pt}$ | (12) |
| ${P_2}Q = 0.5{t_{{\rm{total}}}}\sec {\theta _0}\hat i + {t_{{\rm{total}}}}\hat n$ | (13) |
上文提到基于传输线理论计算的透射系数仅考虑了多层介质中电磁波的纵向传输相位延迟,忽略了横向传输相位延迟。文献[21]通过引入横向传输相位因子对透射系数进行修正,提高了计算精度。因此,为提高多层介质结构厚度较大或入射角较大时等效面模型的计算精度,需对式(11)进一步进行修正,参考文献[21]中结论,引入横向传输相位因子,推导新的透射系数修正公式为:
| ${T \;^m} = T \;{{\rm{e}}^{{\rm{j}}{k_0}\left( {{P_1}Q \cdot \hat i - {P_2}Q \cdot \hat s} \right)}}{{\rm{e}}^{ - {\rm{j}}{k_0}\sin {\theta _0}t'}} \hspace{35pt}$ | (14) |
| $t' = {t_1}\tan {\theta _1} + {t_2}\tan {\theta _2} + \cdot \cdot \cdot + {t_N}\tan {\theta _N}$ | (15) |
利用本文等效面模型方法分别对双层介质平板与金属柜组合结构、建筑物目标进行仿真计算,并与基于传统射线追踪方法的实体模型计算结果相比较,验证本文等效面模型的正确性和高效性。
4.1 双层介质平板与金属柜组合结构双层介质平板与金属柜组合结构模型如图 6所示,其中图 6(a)为实体模型,图 6(b)为等效面模型。模型几何参数在图中均做标识,前介质平板(厚度0.2 m)电参数为 ${\varepsilon _{\rm{r}}} = 4.0 - {\rm{j}}0.24,{\mu _{\rm{r}}} = 1.0$ ;后介质平板(厚度0.1 m)电参数为 ${\varepsilon _{\rm{r}}} = 6.25- {\rm{j}}0.30,{\mu _{\rm{r}}} = 1.0$ 。中心频率为2.5 GHz、带宽2 GHz的垂直极化电磁波沿-X轴方向入射。图 7给出了等效面模型在反射/透射系数相位修正前后与实体模型的1维距离像对比。
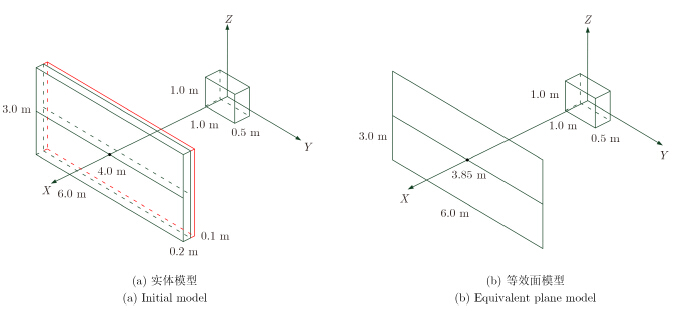
|
图 6 双层介质平板与金属柜组合结构 Fig.6 Two-layered dielectric slab with metal cabinet |
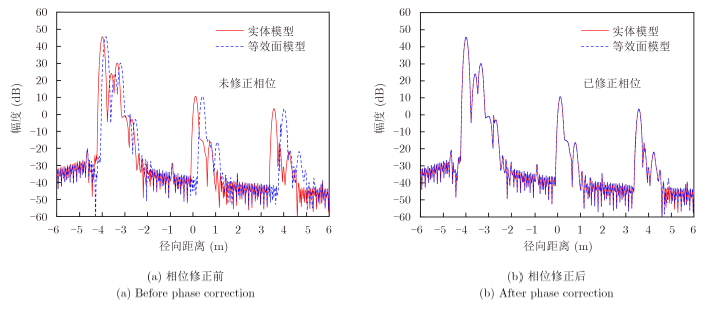
|
图 7 两组模型1维距离像对比 Fig.7 Comparison of range profile between initial model and equivalent plane model |
对比图 7可知,相位修正前等效面模型相对实体模型的1维距离像存在明显的相位延迟,相位修正后两者的1维距离像完全重合。进一步分析可知,1维距离像中的波峰位置与介质分界面、金属柜的理论计算位置完全吻合,但与模型真实位置存在一定的差异,这是因为电磁波在介质中的传播速度比自由空间中慢。
最后,对比两组模型的计算时间,等效面模型的计算效率是实体模型的101倍。显然,随着多层介质平板层数的增加,计算效率将进一步提升,极大地节省了时间成本。仿真结果验证了本文方法的正确性和高效性。
4.2 建筑物模型对图 3所示四室建筑物模型进行仿真计算获取SAR图像,并对比等效面模型在相位修正前后与实体模型仿真结果的差异。建筑物墙体由电磁参数为 ${\varepsilon _{\rm{r}}} = 3.8 - {\rm{j}}0.24,{\mu _{\rm{r}}} = 1$ 的砖块构成,根据上文准则构建等效面模型。入射电磁波中心频率为2.5 GHz、有效带宽为2 GHz,沿水平方向入射,垂直极化,合成孔径角为40°,且孔径角中心角度对应方位角0°。图 8给出了本文等效面模型仿真得到的SAR图像与实体模型的SAR图像对比。
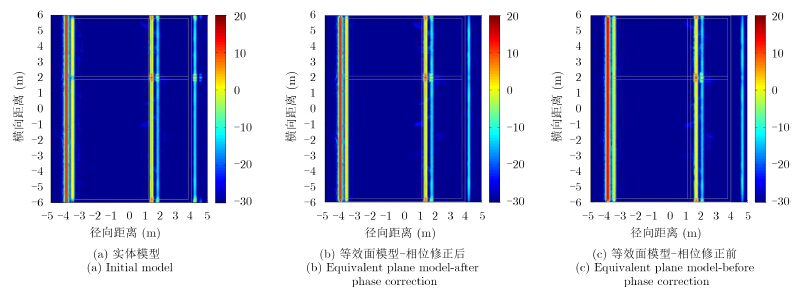
|
图 8 建筑物模型SAR图像对比 Fig.8 Comparison of building model’s SAR images |
由图 8(a)、图 8(b)可知,相位修正后的等效面模型与实体模型仿真得到的SAR图像散射中心的强度、位置分布均吻合良好。图中自左向右分别为5条强度渐弱的直线,分别对应建筑物模型中与观察方向垂直的三面墙 (每面墙有两个侧面分别对应两条直线),理论上应该存在第6条直线,位于SAR图像最右侧,但因为墙壁对电磁波的衰减导致强度很弱,未能在SAR图像中呈现出来。同时,SAR图像中右侧4条直线均在某位置强度发生突变,对照建筑物模型平面图后确定为建筑物内部平行于观察方向的墙壁。进一步对比几何模型发现,SAR图像中散射中心位置滞后于真实几何位置,这是由于电磁波在介质中传播速度比自由空间慢,产生了空间相位延迟。介质墙壁空间延迟通过公式 $D = d \cdot \left( {\sqrt {{\varepsilon _{\rm{r}}}{\mu _{\rm{r}}}} - 1} \right)$ (d为墙壁厚度)计算,理论分析表明文中等效面模型相位修正后计算得到的SAR图像散射中心位置是准确的。由图 8(b)、图 8(c)可知,相位修正能够显著改善等效面模型的计算精度。图 8(c) 为相位修正前的仿真SAR图像,与相位修正后图像对比存在明显的延迟,SAR图像与真实几何模型对比误差较大。
最后,对实体模型和等效面模型的计算效率和内存需求进行定量比较。考虑到计算时间、内存消耗与射线数成正比相关,表 1给出了实体模型与等效面模型在2000根射线入射下的计算时间和峰值内存。对比可知,等效面模型相对实体模型计算效率提高29.2倍,内存消耗降低为实体模型的26.0%。仿真结果验证了等效面模型及其相位修正算法的精确性和高效性。
| 表 1 实体模型与等效面模型计算时间和峰值内存对比 Tab. 1 Comparison of compute time and peak memory between initial model and equivalent plane model |
本文提出了基于传输线理论的多层介质结构等效面模型及其相位修正算法,解决了传输线等效模型无法与射线追踪有效结合的问题,在保证较高计算精度的条件下,实现了对多层介质平板结构及由其构成的超电大复杂介质目标的快速仿真计算,仿真结果验证了本文方法的正确性和高效性。
结合作者之前的工作[17],本文等效面模型方法与改进的蒙特卡洛法(入射射线随机反射或透射,概率取决于反射与透射能量分布)或自适应射线细分法(大幅度减少初始射线,在射线追踪过程中自适应添加射线)相互独立,两者结合能够进一步提高计算效率,降低内存消耗。同时,所有射线追踪与计算均是相互独立的,非常适合开展并行加速。
附录根据等效原理,任意用一个闭合面(Huygens面)S包围目标,闭合面S外散射场E,H由闭合面S上全部电磁场Es,Hs共同产生[24, 25]。本文图 5为多层介质平板结构的传输线等效模型及其等效面模型,假定两组模型的闭合面S无限接近于各自模型与自由空间的分界面。
文中式(7)和式(8)为闭合面S外散射场表达式,根据远场近似条件,有
| $\nabla '{G_0}\left( {{{r}},r'} \right) = - {\rm{j}}k\hat s{G_0}\left( {r,r'} \right)$ | (A-1) |
考虑到入射波入射到多层介质结构后,产生反射场与透射场。下面分别求解反射场与透射场对散射场的贡献。
多层介质平板传输线等效模型在P1点处反射场对散射场贡献为:
| $\begin{array}{*{20}{l}} {{E_1}\left( r \right) = \oint_{{S_{{P_1}}}} {\left[{ - {\rm{j}}\omega \mu \left( {{e_ \rm n} \times {H \!_{{P_1}}}} \right) + \left( {{e_ \rm n} \times {E_{{P_1}}}} \right) \times \nabla '} \right.} }\\ \quad \qquad \ \ {\left. { + \left( {{e_ \rm n} \cdot {E_{{P_1}}}} \right)\nabla '} \right]{G_0}\left( {r,{{}r^\prime \! \! _{{P_1}}} } \right){\rm{d}} {S^\prime \! \!_{{P_1}}} } \end{array}$ | (A-2) |
多层介质平板等效面模型在Q点处反射场对散射场贡献为:
| $\begin{array}{*{20}{l}} {{E_2}\left( r \right) = \oint_{{S_Q}} {\left[{ - {\rm{j}}\omega \mu \left( {{e_ \rm n} \times {H\! _Q}} \right) + \left( {{e_ \rm n} \times {E_Q}} \right) \times \nabla '} \right.} }\\ \quad \qquad \ \ {\left. { + \left( {{e_ \rm n} \cdot {E_Q}} \right)\nabla '} \right]{G_0}\left( {r,{r^\prime \! \! _Q}} \right){\rm{d}}{{S}^\prime} \! \! _Q} \end{array}$ | (A-3) |
| ${H \! _Q} = {H \! _{{P_1}}}{\rm e}^{ - {\rm{j}}k{P_1}Q{ \hat i}} \hspace{55pt}$ | (A-4) |
| ${E \! _Q} = {E \! _{{P_1}}}{{\rm e}^{ - {\rm{j}}k{P_1}Q \hat i}} \hspace{60pt}$ | (A-5) |
| ${G_0}\left( {r,{r^\prime \! \! _Q}} \right) = {G_0}\left( {r,{r^\prime \! \! _{{P_1}}}} \right){{\rm e}^{{\rm{j}}k{P_1}Q \hat s}}$ | (A-6) |
代入上式可得
| ${E_2}\left( r \right) = {E_1}\left( r \right){{\rm e}^{ - {\rm{j}}k{P_1}Q\hat i}}{{\rm e}^{{\rm{j}}k{P_1}Q\hat s}}$ | (A-7) |
为使P1和Q点处反射场对散射场贡献相同,则反射系数应修正为:
| ${R^m} = R{{\rm e}^{{\rm{j}}k{P_1}Q\hat i}}{{\rm e}^{ - {\rm{j}}k{P_1}Q\hat s}} = R{{\rm e}^{{\rm{j}}k{P_1}Q\left( {\hat i - \hat s} \right)}}$ | (A-8) |
多层介质平板传输线等效模型在P2点处透射场对散射场贡献为:
| $\begin{array}{*{20}{l}} {{E_1}\left( r \right) = \oint_{{S_{{P_2}}}} {\left[{ - {\rm{j}}\omega \mu \left( {{e_{\rm{n}}} \times {H_{{P_2}}}} \right) + \left( {{e_{\rm{n}}} \times {E_{{P_2}}}} \right) \times \nabla '} \right.} }\\ \quad \qquad \ \ {\left. { + \left( {{e_{\rm{n}}} \cdot {E_{{P_2}}}} \right)\nabla '} \right]{G_0}\left( {r,{r^\prime \! \! _{{P_2}}} } \right){\rm{d}}{S^\prime \! \! _{{P_2}}} } \end{array}$ | (A-9) |
多层介质平板等效面模型在Q点处透射场对散射场贡献为:
| $\begin{array}{*{20}{l}} {{E_2}\left( r \right) = \oint_{{S_Q}} {\left[{ - {\rm{j}}\omega \mu \left( {{e_{\rm{n}}} \times {H\! _Q}} \right) + \left( {{e_{\rm{n}}} \times {E\! _Q}} \right) \times \nabla '} \right.} }\\ \quad \qquad \ \ {\left. { + \left( {{e_{\rm{n}}} \cdot {E\! _Q}} \right)\nabla '} \right]{G_0}\left( {r,{r^\prime} \! \! _Q} \right){\rm{d}}{S^\prime \! \! _Q} } \end{array}$ | (A-10) |
| ${H_Q} = {H_{{P_2}}}{{\rm {e}}^{ - {\rm{j}}k{P_1}Q\hat i}} \hspace{55pt}$ | (A-11) |
| ${E_Q} = {E_{{P_2}}}{{\rm {e}}^{ - {\rm{j}}k{P_1}Q\hat i}} \hspace{60pt}$ | (A-12) |
| ${G_0}\left( {r,{r^\prime \! \! _Q}} \right) = {G_0}\left( {r,{r^\prime \! \! _{{{P}_2}}}} \right){e^{{\rm{j}}k{P_2}Q\hat s}}$ | (A-13) |
代入上式可得
| ${E_2}\left( r \right) = {E_1}\left( r \right){{\rm{e}}^{ - {\rm{j}}k{P_1}Q\hat i}}{{\rm{e}}^{{\rm{j}}k{P_2}Q\hat s}}$ | (A-14) |
为使P2和Q点处透射场对散射场贡献相同,则透射系数应修正为:
| ${T^m} = T \,{{\rm{e}}^{{\rm{j}}k{P_1}Q\hat i}}{{\rm{e}}^{ - {\rm{j}}k{P_2}Q\hat s}} = T \,{{\rm{e}}^{{\rm{j}}k\left( {{P_1}Q\hat i - {P_2}Q\hat s} \right)}}$ | (A-15) |
文中式(14),式(15)给出了多层介质平板结构厚度较大或入射角较大时透射系数的相位修正公式,其中引入了传统传输线理论中忽略的横向传输分量相位因子,推导过程见参考文献[21]。
| [1] | Setlur P, Alli G, and Nuzzo L. Multipath exploitation in through-wall radar imaging via point spread functions[J]. IEEE Transactions on Image Processing, 2013, 22(12): 4571-4586.
( 1) 1) |
| [2] | Jin Tian, Chen Bo, and Zhou Zhi-min. Image-domain estimation of wall parameters for autofocusing of throughthe- wall SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1836-1843.( 1) 1) |
| [3] | Chang P C, Burkholder R J, Volakis J L, et al.. Highfrequency EM characterization of through-wall building imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(5): 1375-1387.
( 3) 3) |
| [4] | Rotbart A and Boag A. A multilevel non-uniform grid algorithm for acceleration of volumetric integral equation based solvers for analysis of arbitrarily shaped dielectric radomes[C]. IEEE International Conference on Microwaves, Communications, Antennas and Electronic Systems, Tel Aviv, 2011, DOI: 10.1109/COMCAS.2011.6105944.
( 1) 1) |
| [5] | Lu C C. A fast algorithm based on volume integral equation for analysis of arbitrarily shaped dielectric radomes[J]. IEEE Transactions on Antennas and Propagation, 2003, 51(3): 606-612.( 1) 1) |
| [6] | 陈博韬. 低空目标与环境复合电磁散射特性研究[D]. [博士论 文], 西安电子科技大学, 2012: 87-110. Chen Bo-tao. Research on the composite electromagnetic scattering from low altitude target and the environment[D].[Ph.D. dissertation], Xidian University, 2012: 87-110. (  1) 1) |
| [7] | 王新民. 合成孔径雷达原始回波模拟的研究[D]. [博士论文], 中国科学院电子学研究所, 2007: 15-57. Wang Xin-min. Study on raw signal simulation of synthetic aperture radar[D]. [Ph.D. dissertation], Institute of Electronics Chinese Academy of Sciences, 2007: 15-57. (  1) 1) |
| [8] | Chow W C. Waves and Fields in Inhomogeneous Media[M]. New York: Nostrand Reinhold, 1990: 45-206.
( 1) 1) |
| [9] | Demarest K, Plumb R, and Huang Z. FDTD modeling of scatterers in stratified media[J]. IEEE Transactions on Antennas and Propagation, 1995, 43(10): 1164-1168.
( 1) 1) |
| [10] | Isleifson D, Jeffrey I, Shafai L, et al.. An efficient scatteredfield formulation for objects in layered media using the FVTD method[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(11): 4162-4170.
( 1) 1) |
| [11] | Michalski K A and Zheng D. Electromagnetic scattering and radiation by surfaces of arbitrary shape in layered media, Part I: Theory[J]. IEEE Transactions on Antennas and Propagation, 1990, 38(3): 335-344.
( 1) 1) |
| [12] | Bishay S T,Abo-Seida O M,and Shoeib H S. Electromagnetic radiation fields in three-layered media with rough interfaces[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 4006-4013.( 1) 1) |
| [13] | Yang Pei-gang, Nie Zai-ping, Que Xiao-feng, et al.. Application of CFIE with hierarchical vector basis functions for EM scattering from hybrid metal-dielectric objects with MLFMA[C]. 2012 10th International Symposium on Antennas, Propagation & EM Theory, Xian, 2012: 967-970.
( 1) 1) |
| [14] | Ling H, Chou R C, and Lee S W. Shooting and bouncing rays: calculating the RCS of an arbitrarily shaped cavity[J]. IEEE Transactions on Antennas and Propagation, 1989, 37(2): 194-205.
( 1) 1) |
| [15] | Didascalou D, Schafer T M, Weinmann F, et al.. Raydensity normalization for ray-optical wave propagation modeling inarbitrarily shaped tunnels[J]. IEEE Transactions on Antennas and Propagation, 2000, 48(9): 1316-1325.
( 1) 1) |
| [16] | 董纯柱, 殷红成, 王超. 基于射线管分裂方法的SAR场景快速 消隐技术[J]. 雷达学报, 2012, 1(4): 436-440. Dong Chun-zhu, Yin Hong-cheng, and Wang Chao. A fast hidden surface removal approach for complex SAR scene based onadaptive ray-tube splitting method[J]. Journal of Radars, 2012, 1(4): 436-440. (  1) 1) |
| [17] | 张磊, 王超, 董纯柱, 等. 分层介质目标电磁散射计算的快速射 线追踪方法[J]. 电波科学学报, 2015, 30(2): 208-216. Zhang Lei, Wang Chao, Dong Chun-zhu, et al.. Fast raytracing method for electromagnetic scattering computation of multi-layered dielectric structure[J]. Chinese Journal of Radio Science, 2015, 30(2): 208-216. (  3) 3) |
| [18] | Le C, Dogaru T, Nguyen L, et al.. Ultrawideband (UWB) radar imaging of building interior: measurements and predictions[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(5): 1409-1420.
( 1) 1) |
| [19] | Dogaru T, Liao D H, and Le C. Three-dimensional radar imaging of a building[R]. ARL-TR-6295, U. S. Army Research Laboratory: Adelphi, MD, 2012.
( 1) 1) |
| [20] | Wang Gu, Yuan Lei, Wang Tao-sheng, et al.. RCS calculation of complex targets shielded with plasma based on visual GRECO method[C]. 2009, 3rd IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Beijing, 2009: 950-953.
( 1) 1) |
| [21] | Meng Hong-fu, Dou Wen-bin, Chen Tian-tian, et al.. Analysis of radomeusing aperture integration-surface integration method with modified transmission coefficient[J]. Journal of Infrared, Millimeter Terahertz Waves, 2009, 30(2): 199-210.
( 7) 7) |
| [22] | Ip H P and Rahmat-samii Y. Analysis and characterization of multilayered reflector antennas: rain/snow accumulation and deployable membrane[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(11): 1593-1605.
( 3) 3) |
| [23] | Ishimaru A. Electromagnetic Wave Propagation, Radiation, and Scattering[M]. Englewood Cliffs, NJ: Prentice Hall, 1991: 31-76.
( 3) 3) |
| [24] | 杨儒贵. 高等电磁理论[M]. 北京: 高等教育出版社, 2008: 166-180. Yang Ru-gui. Advanced Electromagnetic Theory[M]. Beijing: Higher Education Press, 2008: 166-180.
( 3) 3)
|
| [25] | Kim H and Ling H. Electromagnetic scattering from an inhomogeneous object by ray tracing[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(5): 517-525.( 2) 2) |


