低空目标探测问题是雷达信号处理领域的难点问题。低空环境下,目标直接回波与地面反射回波共同进入天线主瓣,形成多径干扰,造成较大的俯仰角测量误差。作为一种高分辨波达方向估计算法,多重信号分类 (MUSIC) 算法在目标角度估计方面具有优良性能,但传统的MUSIC算法无法处理多径相关信号,且运算量较大,实时处理能力较弱。为此,专家学者从不同角度对MUSIC算法进行改进。在处理信号相干方面,文献[1]采用空间平滑的方法,通过子阵列协方差矩阵加权平均取代原来的信号协方差矩阵,但阵列有效孔径减少,角度估计分辨率降低;文献[2]提出将协方差矩阵重构为Hermitian Toeplitz矩阵,但在目标相关性较强时仍不能完全解相干;文献[3]提出完全解相干算法,通过对快拍数据协方差矩阵虚拟平滑实现相干信号的完全解相干,但将该方法具体应用于多径环境下尚需研究。在解决运算量方面,文献[4]将遗传算法引入波达方向估计,改变了传统的逐点搜索谱峰方式,但只能搜索到全局最优点,无法实现多谱峰搜索。文献[5],文献[6]提出的小生境遗传算法(Niched Genetic Algorithms,NGA)能够实现搜索多个谱峰,但小生境的构造和完善机制比较复杂。文献[7]提出自适应步长萤火虫算法寻找函数多个极值点的思想,能够较好完成多峰函数寻优。
为提高低空多径环境下目标波达方向的估计精度和速度,本文提出一种基于自适应萤火虫算法的MUSIC方法。将完全解相干算法应用于低空环境下以解决信号多径相干问题,根据MUSIC算法原理建立空间谱函数作为寻优函数,采用自适应步长萤火虫算法实现多谱峰的快速搜索。仿真结果表明,该方法能够有效解决低空环境下目标波达方向估计问题。
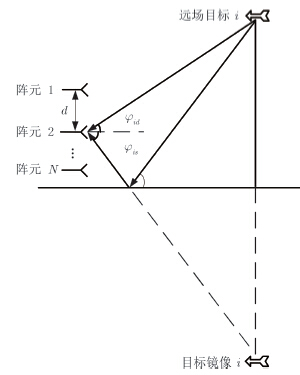
2 低空多径环境下阵列接收信号模型如图 1,采用窄带雷达探测P个互不相关的远场目标,目标直接回波和地面反射回波同时进入垂直放置的N元均匀线阵。多径反射包括镜面反射与漫反射,而镜面反射占主要部分,因此反射回波仅考虑理想的镜面反射。阵列接收信号为:
|
图 1 阵列接收信号模型 Fig.1 Model of the received array signal |
| $\begin{aligned} X(t) = & A(\varphi)S(t) + {n_1}(t)\\ = & {[ {{x_1}(t)} \quad {{x_2}(t)} \ \ \ldots \ \ {{x_N}(t)} ]^{\rm{T}}} \end{aligned}$ | (1) |
导向矩阵可表示为:
| $A(\varphi) = [ {a({\varphi _{1d}})} \quad {a({\varphi_{1s}})} \ \ \cdots \ \ {a({\varphi _{Pd}})} \quad {a({\varphi _{Ps}})} ]$ | (2) |
信号矩阵为:
| $S(t) = {[ {{s_{1d}}(t)} \quad {{s_{1s}}(t)} \quad \cdots \quad {{s_{Pd}}(t)} \quad {{s_{Ps}}(t)} ]^{\rm{T}}}$ | (3) |
n1(t)=[n1(t) n2(t) ··· nN(t)]T,假定n1(t),n2(t),···,nN(t)为互不相关的零均值高斯白噪声,且与P个目标信号互不相关。
3 完全解相干MUSIC算法 3.1 算法原理由于多径信号的相关性,阵列接收信号的协方差阵将不满足Toeplitz矩阵的要求,即信号子空间与噪声子空间的正交性不再满足,特征信号矢量发散到噪声子空间中,使得传统MUSIC算法失效。为此,学者们提出了前后向平滑MUSIC算法、改进MUSIC算法(Improved MUSIC,IMUSIC)等,虽然能在一定程度上去相关,但在低空多径、低信噪比的条件下,仍不能完全消除信号相关性,导致个别峰值被遗漏。因此,本文将完全解相干算法引入低空多径信号处理中。
完全解相干算法将每个快拍阵列接收的信号组成一个矩阵,通过矩阵内部虚拟平滑来解相干[3],其具体方法如下:
若设y1(t)=X(t),则:
| $\begin{aligned} {y_2}(t) = & A(\varphi ){Λ ^*}S(t) + {n_2}(t)\\ = & {[x_2^ * (t),{x_1}(t),\cdots ,{x_{N - 1}}(t)]^{\rm{T}}} \end{aligned}$ | (4) |
| $\begin{aligned} Λ = {\rm{diag}}\left( {{{\rm{e}}^{{\rm{j}}\frac {\large{{2π d}}} {\large{\lambda }} \sin ({\varphi _{1d \, }})}}} \quad {{{\rm{e}}^{{\rm{j}}\frac {\large{{2π d}}} {\large{\lambda }} \sin ({\varphi _{1s \, }})}}} \quad \cdots \right.\\ \left. {{{\rm{e}}^{{\rm{j}}\frac {\large{{2π d}}} {\large{\lambda }} \sin ({\varphi _{Pd \, }})}}} \quad {{{\rm{e}}^{{\rm{j}}\frac {\large{{2π d}}} {\large{\lambda }} \sin ({\varphi _{Ps \, }})}}} \right)\hspace{17pt} \end{aligned}$ | (5) |
| ${{\bf{n}}_{\rm{2}}}(t) = {[ {n_2^ * (t)} \quad {{n_1}(t)} \quad \cdots \quad {{n_{N - 1}}(t)} ]^{\rm{T}}}$ | (6) |
依此类推,有:
| $\begin{aligned} {y_N}(t) & = A(\varphi ){({\Lambda ^*})^{N - 1}}S(t) + {n_N}(t)\\ & = {\left[{x_N^ * (t) \quad x_{N - 1}^ * (t) \quad \cdots \quad {x_1}(t)} \right]^{\rm{T}}} \end{aligned}$ | (7) |
| ${n_N}(t) = {[n_N^ * (t) \quad n_{N - 1}^ * (t) \quad \cdots \quad {n_1}(t)]^{\rm{T}}}$ | (8) |
将y1(t),y2(t),···,yN(t)组成矩阵Y(t),将n1(t),n2(t),···,nN(t)组成噪声矩阵N(t)=[n1(t)n2(t) ··· nN(t)]T,则有:
| $\begin{aligned} {Y}(t) = & [\begin{array}{*{20}{c}}\!\! {{{ \, y}_{\rm{1}}}(t)}& {{y_{\rm{2}}}(t)} & \cdots & {{y_N}(t) \, } \end{array}\!\!]\\ = & \left[\!\!\! {\begin{array}{*{20}{c}} {{x_1}(t)} & {x_2^ * (t)} & {x_3^ * (t)} & \cdots & {x_N^ * (t)}\\ {{x_2}(t)} & {{x_1}(t)} & {x_2^ * (t)} & \cdots & {x_{N - 1}^ * (t)}\\ {{x_3}(t)} & {{x_2}(t)} & {{x_1}(t)} & \cdots & {x_{N - 2}^ * (t)}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ { \, {x_N}(t)} & {{x_{N - 1}}(t)} & {{x_{N - 2}}(t)} & \cdots & {{x_1}(t)} \end{array}} \!\!\! \right]\\ = & A({\varphi })[\!\! \begin{array}{*{20}{c}} { \, S(t)} & {{{\Lambda}^{*}}S(t)} & \cdots & {{{({{\Lambda }^*})}^{N - 1}}S(t) \, } \end{array}\!\!] \\ & + N(t) \\ = & A({\varphi}){R_{s}}{A^{\rm{H}}}({\varphi }) + N(t) \end{aligned}$ | (9) |
| $\begin{aligned} R & = E[x_1^*(t)Y(t)]\\ & = A(\varphi )E[x_1^*(t){R_s}]{A^{\rm{H}}}(\varphi ) + \sigma _{\rm{n}}^2I\\ & = A(\varphi ){R_s^{ \prime }}{A^{\rm{H}}}(\varphi ) + \sigma _{\rm{n}}^2I \end{aligned}$ | (10) |
I为N阶单位阵,相关矩阵为:
| $\begin{aligned} R_s^\prime & = {\rm{diag}}\left[{{{s_{1d}^\prime }}(t) \quad {{s_{1s}^\prime }}(t) \quad \cdots \quad {{s_{Pd}^\prime }}(t) \quad {{s_{Ps}^\prime }}(t)} \right]\\ & = {\left[\!\! {\begin{array}{*{20}{c}} {{{s_{1d}^\prime }}(t)} & 0 & 0 & 0 & 0 \\ 0 & {{{s_{1s}^\prime }}(t)} & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & {{{s_{Pd}^\prime }}(t)} & 0 \\ 0 & 0 & 0 & 0 & {{{s_{Ps}^\prime }}(t)} \end{array}} \!\! \right]_{2P \times 2P}} \end{aligned}$ | (11) |
| $\begin{aligned} {{s_{id}^\prime }}(t) & = {\rm{E}}[{s_{id}}(t)x_1^ * (t)]\\ & = {\rm{E}}\left\{ {{s_{id}}(t) \left [\sum\limits_{j = 1}^P {s_{jd}^ * } (t) + \sum\limits_{j = 1}^P {s_{js}^ * } (t) + n_1^*(t) \right]} \right\}\\ & = {\rm{E}}[{s_{id}}(t)s_{id}^ * (t) + {s_{id}}(t)s_{is}^ * (t)]\\ & = \left( {1 + {\rho _i}{{\rm{e}}^{ - {\rm{j}}{\phi _i}}}} \right)\sigma _{{\rm{s}}\_i}^2 \end{aligned}$ | (12) |
| $\begin{aligned} {{s_{is}^prime }}(t) & = {\rm{E}}[{s_{is}}(t)x_1^ * (t)]\\ & = {\rm{E}}\left\{ {{s_{is}}(t)\left[{\sum\limits_{j = 1}^P {s_{jd}^ * } (t) + \sum\limits_{j = 1}^P {s_{js}^ * } (t) + n_1^*(t)} \right]} \right\}\\ & = {\rm{E}}[{s_{is}}(t)s_{id}^ * (t) + {s_{is}}(t)s_{is}^ * (t)]\\ & = \left( {{\rho _i} + {{\rm{e}}^{{\rm{j}}{\phi _i}}}} \right){\rho _i}\sigma _{{\rm{s}}\_i}^2 \end{aligned}$ | (13) |
则得到式(14),因为0<ρi<1,$\left| {{{\rm{e}}^{ - {\rm{j}}{\phi _i}}}} \right| \ne 0$ ,所以$(1 + {\rho _i}{{\rm{e}}^{ - {\rm{j}}{\phi _i}}})\sigma _{{\rm{s}}\_i}^2 \ne 0$ ,$\left( {{\rho _i} + {{\rm{e}}^{{\rm{j}}{\phi _i}}}} \right){\rho _i}\sigma _{{\rm{s}}\_i}^2 \ne 0$ ,故${s_i^\prime } \ne 0$ ,rank(${R_s^\prime }$ )=2P,从而相关矩阵R为满秩矩阵。可见,通过解相干算法消除了相干信号之间的干扰。
| $\begin{aligned} {{R_{s}^\prime }} & \!\! = \!\! {\rm{diag}}\left( {{{s_{1d}^\prime }}(t) \quad {{s_{1s}^\prime }}(t) \quad \cdots \quad {{s_{Pd}^\prime }}(t) \quad {{s_{Ps}^\prime }}(t)} \right)\\ & \!\! = \!\! {\left[\!\! {\begin{array}{*{20}{c}} {(1 \! + \! {\rho _1}{{\rm{e}}^{ \! - \! {\rm{j}}{\phi _1}}})\sigma _{{\rm{s}}\_1}^2} & 0 & \cdots & 0 & 0 \\ 0 & {(\rho _1^2 \! + \! {\rho _1}{{\rm{e}}^{{\rm{j}}{\phi _1}}})\sigma _{{\rm{s}}\_1}^2} & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & {(1 \! + \! {\rho \! \; \! _P} \,{{\rm{e}}^{ \! - \! {\rm{j}}{\phi _P}}})\sigma _{{\rm{s}}\_P}^2} & 0 \\ 0 & 0 & \cdots & 0 & {(\rho _P^2 \! + \! {{\rho} \! \; \! _{P}} \,{{\rm{e}}^{{\rm{j}}{\phi _P}}})\sigma _{{\rm{s}}\_P}^2} \end{array}} \!\! \right] \!\! } \end{aligned}$ | (14) |
在信号模型建立的过程中,仅考虑了理想平面情况下镜面反射,而实际反射面都是存在粗糙度的。根据表面粗糙度理论[9],当表面高度起伏Δh<λ/(8sinφ)时,符合瑞利判据,表明反射面处在第1 Fresnel反射区内,可忽略漫散射影响,将镜面反射系数幅值校正为${\rho_i^\prime } $ =ρiρ0,其中ρi为理想镜面反射系数,而 ${\rho _0}| = {(\exp {\rm{[}} - {(4\pi {\sigma _{\rm{h}}}\sin \psi /\lambda )^2}{\rm{])}}^{1/2}}$ 为相对平坦地面的镜散射系数均方根值,σh为表面为正态分布的表面高度变化均方根值,φ为掠射角。ρs>0,故$(1 + {\rho_i^\prime } {{\rm{e}}^{ - {\rm{j}}{\phi _i}}})\sigma _{{\rm{s}}\_i}^2 \ne 0$ ,$\left( {{{\rho_i^\prime }} + {{\rm{e}}^{{\rm{j}}{\phi _i}}}} \right){\rho_i^\prime }\sigma _{{\rm{s}}\_i}^2 \ne 0$ 仍然成立,因此理论上讲在反射面满足瑞利判据的情况下本文方法是适用的。随着反射面粗糙度增大,Δh不再满足瑞利判据,漫散射功率逐渐占据主导地位,镜反射模型不再成立,本文方法将失效。
4 自适应步长萤火虫算法若按照传统方法逐点搜索空间谱函数峰值,运算量大且实时性差。研究表明,MUSIC算法的主要计算量在谱峰搜索这一环节,为此专家学者纷纷提出各种智能优化算法来解决谱峰搜索问题。自然界中萤火虫发光越亮,越能吸引同伴向其聚拢,受到这一现象的启发,文献[10]在2005年提出萤火虫群智能优化算法(Glowworm Swarm Optimization,GSO)。作为一种群智能优化算法,GSO算法能够克服诸多经典算法寻找空间谱函数容易陷入局部最优或只能寻找全局最优的不足,准确搜索到所有的谱峰。在此,首先介绍基本的萤火虫算法,随后提出自适应步长萤火虫算法(Self-Adaptive Step Glowworm Swarm Optimization,ASGSO)以提高谱峰搜索速度和精度。
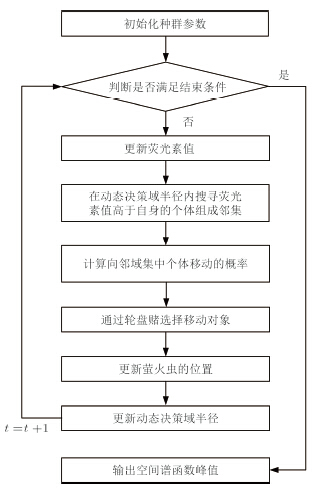
4.1 基本萤火虫算法如图 2所示[11],设目标函数搜索空间中随机分布有n个萤火虫,每个萤火虫在t时刻的荧光素值记为li(t) (i=1,2,···,n),荧光素值越大,表明该个体的目标函数值也越高,对其他个体的吸引力越大。每个萤火虫在t时刻的动态决策域半径记为$r_d^i$ (t),0<$r_d^i$ (t)<rs,rs为萤火虫个体最大感知半径。凡处在第i个萤火虫动态决策域半径且荧光素值高于li(t)的个体均被纳入i的邻域集Ni(t)。i向Ni(t)中个体移动的概率与相应个体的荧光素值有关,荧光素值越高,对i的吸引力越大。显然,初始随机分布的个体会逐渐向函数极值点不断聚集。
|
图 2 GSO算法流程 Fig.2 Flow chart of GSO algorithm |
通过研究可以发现,GSO算法存在收敛速度与寻优精度之间的矛盾。如果搜索步长较大,虽然搜索速度较快,但部分极值可能被遗漏;而如果减小搜索步长,虽然寻优精度满足要求,但收敛速度较慢,难以满足实时性的要求。而且,受固定步长的限制,在接近峰值时,可能发生在极值附近震荡而无法取到极值的情况,造成较大误差[12, 13]。因此,本文提出一种自适应步长的萤火虫算法,在搜索初期采用较大步长提高搜索速度,而在接近峰值时,自适应地减小步长,保证寻优精度。
设第i个萤火虫的邻域集Ni(t)中含有m个萤火虫(m≤nt),设x(t)代表萤火虫在t次迭代时的位置,则第i个萤火虫到这m个萤火虫的距离${d_{ij}}(t) = \left\| {{x_j}(t) - {x_i}(t)} \right\|$ ,(j=1,2,···,m),平均距离为:
| $\bar d_i(t) = \frac{{\sum\limits_{j = 1}^m {{d_{ij}}(t)} }}{m} = \frac{{\sum\limits_{j = 1}^m {\left\| {{x_j}(t) - {x_i}(t)} \right\|} }}{m}$ | (15) |
对自适应步长si(t)做出规定:当$\bar d_i$ (t)<si(t–1)且$\bar d_i$ (t)≠0时,si(t)=si(t–1)/2;当$\bar d_i$ (t)>si(t–1)且$\bar d_i$ (t)≠0时,si(t)=si(t–1)·2。
相对于固定步长的基本萤火虫算法,自适应步长萤火虫算法无论是精度还是运算速度都得到了提高,这是由于在运算初期,萤火虫个体均匀分布,具有高荧光值的个体吸引其他个体向其移动,此时步长相应增大以快速向局部极值移动,提高了寻优速度;在萤火虫聚拢到峰值附近时,固定步长可能导致萤火虫在峰值点附近震荡而始终无法达到峰值,自适应步长此时逐步缩短步长,渐近地达到峰值。因此,自适应步长萤火虫算法具有更高的估计精度和更好的实时性。
4.3 参数选择问题在低空、多目标环境下为准尽可能搜索到所有谱峰需结合目标参数情况进行合理设置。文献[14]经过对大量多极值函数的研究实验,得出具有最佳谱峰搜索能力情况下的部分参数取值如表 1所示。其中α为荧光素挥发因子,β为动态决策域半径更新率,Γ为荧光素更新率,l0为初始荧光素值,nt为个体邻域集中萤火虫数目的阈值,s为移动步长。最大感知半径rs和初始感知范围rd(0)需根据具体应用环境进行分析,在谱峰搜索算法中必须保证最大感知半径小于两谱峰的间距,否则较低谱峰附近的萤火虫会因发现另一更高谱峰而向其聚拢,导致较低谱峰的漏检。同理,初始感知范围rd(0)过大将导致萤火虫群体忽略个别较低谱峰造成漏检,过低则会影响谱峰搜索速度下降。
| 表 1 算法参数取值 Tab. 1 Value of GSO algorithm parameters |
设3个低空目标的参数如表 2所示,直接回波和反射回波总相位差(包括地面反射导致的相移和波程差导致的相位差)分别为π,π/2,0。阵元N=30,SNR=10 dB (仿真中的信噪比均指单个阵元接收的单快拍信噪比),波长λ=d/2,快拍数snap=10,搜索范围为[–30°,30°]。
| 表 2 目标参数 Tab. 2 Parameters of targets |
仿真1 解相干算法性能分析
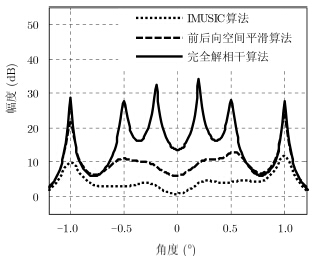
前后向空间平滑算法和IMUSIC算法是MUSIC算法中两种经典的解相干算法,为分析完全解相干算法的解相干性能,将上述3种算法进行比较,设前后向空间平滑算法将30个阵元分为6个子阵,每个子阵中包括25个阵元。仿真结果如图 3,在存在相干信号条件下,±0.5°处IMUSIC算法未形成谱峰,前后向空间平滑算法形成谱峰但不够明显,而且+0.5°处谱峰位置存在一定偏差;±0.2°处前后向空间平滑算法未形成谱峰,IMUSIC算法在±0.2°附近形成不明显谱峰,而完全解相干MUSIC算法能够在不同波程差的条件下较好克服多径相干的不利影响,准确分辨出6个不同的角度。
|
图 3 解相干效果对比图 Fig.3 Comparison of de-correlation performance |
仿真2 算法准确性分析
仿真2针对表 2给出的3个目标,通过50次蒙特卡罗仿真,分析不同算法的准确性。算法的基本参数设置依据表 1,表 3。对于ASGSO和GSO算法,分析3个俯仰角具体情况,发现6个谱峰中最小间隔是0.3°。为保证位于某一谱峰附近的值不致因搜索到另一更高谱峰后全部移向更高谱峰,设定萤火虫个体最大感知半径rs为0.2°,初始感知范围为0.1°。除步长每代自适应地更新外,ASGSO算法其他参数设置与GSO算法相同。表 3中L为遗传算法编码位数,为与GSO,ASGSO移动步长相当以具有可比性,取为12位。r为小生境半径,设为6个谱峰中最小间距的一半,即0.15°。p为惩罚函数值,Pc为交叉概率,Pm为变异概率,取仿真常用值。3种智能算法最大迭代代数G=100。
| 表 3 NGA算法参数取值 Tab. 3 Value of NGA algorithm parameters |
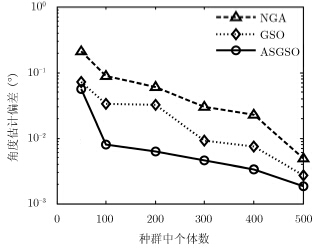
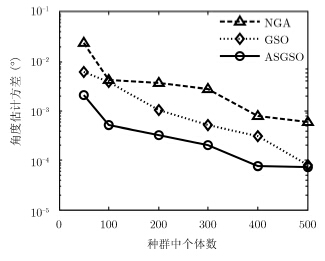
图 4,图 5为SNR=10 dB时,不同个体数下3种算法的估计误差和方差,分析两图可知,各算法的精度都随着种群中个体数的增加得到提高,这是由于随着个体数增加,对取值范围内的空间谱函数极值的搜索更加充分,搜索到的局部极值更加逼近极值真实值,最终搜索到6个目标真实俯仰角的成功率提高。对比3种算法,ASGSO算法的估计偏差和估计方差最小,精确度最高。
|
图 4 不同个体数下估计偏差 Fig.4 Estimate deviation under different individual numbers |
|
图 5 不同个体数下估计方差 Fig.5 Estimate variance under different individual numbers |
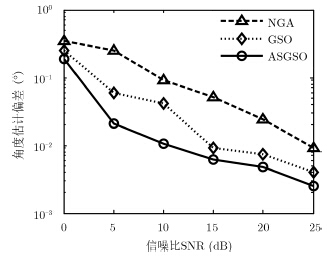
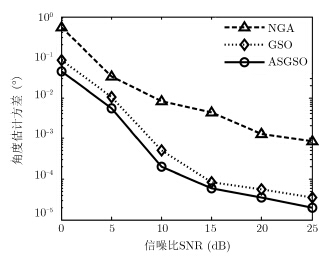
图 6,图 7为种群个体数N=300时,不同信噪比条件下估计偏差和方差。分析两图可知,各算法的精度都随着信噪比的增加得到提高,这是由于随着信噪比增大,空间谱函数峰值增大,群体中个体聚拢到真实极值的概率随之增大,从而提高了角度估计精度。对比3种算法,ASGSO算法的估计偏差和估计方差最小,精确度最高。
|
图 6 不同信噪比下的估计偏差 Fig.6 Estimate deviation under different SNRs |
|
图 7 不同信噪比下的估计方差 Fig.7 Estimate variance under different SNRs |
仿真3 算法时效性分析
在解相干的基础上,仿真3就ASGSO,GSO,NGA算法在同等条件下的时间性能进行研究,并与逐点搜索算法进行比较。经过100次蒙特卡罗仿真,表 4给出了逐点搜索MUSIC算法100次谱峰搜索总用时。表 5给出了SNR=10 dB时,不同个体数下,3种优化算法完成100次搜索总用时。
| 表 4 MUSIC算法步长与时间对应关系(s)
Tab. 4 Relationship between step and time of MUSIC algorithm (s) |
| 表 5 优化算法时间对比表(s) Tab. 5 Time comparison of different optimized algorithms (s) |
分析表 5可见,相同个体数下,ASGSO运算用时最短,而GSO在个体数较多的情况下,运算速度次之,在个体数目较少的情况下,运算速度最差。
结合图 4和图 5,对比分析表 4和表 5发现,逐点搜索MUSIC算法的精度主要取决于搜索步长,步长每缩小一个量级,搜索用时相应增大约一个量级[15],要实现高精度搜索需要大量时间。与之相比,智能算法特别是ASGSO算法可通过控制种群中个体数提高测角精度,达到相同精度的时间消耗更小,这是其主要优点。但个体数提高也不是无限的,随着个体数的增加,智能算法的运算量增大,算法实时性下降,不利于实际运用。所以,需要从精度和速度两个方面进行权衡考虑。
6 结束语传统的MUSIC算法不适用于低空多径环境下目标波达方向估计,且实时性较差。通过完全解相干算法消除多径信号的相关性,可使MUSIC算法适用于低空环境。通过引入GSO算法改变搜索模式能提高搜索速度,减少时间和空间资源消耗,但GSO收敛速度慢,后期可能因在峰值附近震荡而导致寻优精度不够高,据此提出改进的ASGSO算法,提高了收敛速度和寻优精度,并通过3组仿真,验证了该方法的解相干性优于IMUSIC算法和传统MUSIC算法,时效性和准确性优于NGA,GSO算法以及逐点搜索式MUSIC算法。
本文主要针对1维波达方向估计提出采用ASGSO改进空间谱函数搜索方式以提高准确性和时效性的思路,该方法可扩展到多维空间的角度、多普勒等参数的联合估计,为群优化算法进一步应用于DOA估计提供有益的参考和借鉴。
| [1] | 杨雪亚, 陈伯孝, 赵光辉, 等. 基于二维空间平滑的波束域 MUSIC算法[J]. 系统工程与电子技术, 2010, 32(5): 895-899. Yang Xue-ya, Chen Bai-xiao, Zhao Guang-hui, et al.. Beamspace MUSI Cmethod based on 2D spatial smoothing[J]. Systems Engineering and Electronic, 2010, 32(5): 895-899. (  1) 1) |
| [2] | 童宁宁, 郭艺夺, 王光明. 米波雷达低角跟踪环境下的修正 MUSIC算法[J]. 现代雷达, 2008, 30(10): 29-32. Tong Ning-ning, Guo Yi-duo, and Wang Guang-ming. Modified MUSIC algorithm in meter-band radar low-angle tracking environment[J]. Modern Radar, 2008, 30(10): 29-32. (  1) 1) |
| [3] | 朱圣棋, 廖桂生, 李海, 等. 基于数据矩阵的非圆相干信号完全 解相干算法[J]. 系统工程与电子技术, 2009, 31(1): 21-24. Zhu Sheng-qi, Liao Gui-sheng, Li Hai, et al.. DOA estimation of coherent signals based on data matrix[J]. Systems Engineering and Electronics, 2009, 31(1): 21-24. (  2) 2) |
| [4] | 侯姗姗, 谢庆, 廖峰, 等. 基于超声阵列传感器与遗传 MUSIC的局放源波达方向估计[J]. 电测与仪表, 2014, 51(5): 11-14. Hou Shan-shan, Xie Qing, Liao Feng, et al.. Source DOA estimation based on ultrasonic array sensor and Genetic MUSIC[J]. Electrical Measurement & Instrumentation, 2014, 51(5): 11-14. (  1) 1) |
| [5] | 赵远东, 汪怡. 基于均分法的小生境遗传算法[J]. 南京信息工 程大学学报(自然科学版), 2013, 5(6): 553-556. Zhao Yuan-dong and Wang Yi. Niche genetic algorithm research based on average method[J]. Journal of Nanjing University of Information Science and Technology: Natural Science Edition, 2013, 5(6): 553-556. (  1) 1) |
| [6] | 陈彦龙, 张培林, 李胜, 等. 面向多峰函数的自适应小生境量子 进化算法[J]. 系统工程与电子技术, 2014, 36(2): 403-408. Chen Yan-long, Zhang Pei-lin, Li Sheng, et al.. Adaptive niche quantum evolutionary algorithm for multimodal function[J]. Systems Engineering and Electronic, 2014, 36(2): 403-408. (  1) 1) |
| [7] | 欧阳喆, 周永权. 自适应步长萤火虫优化算法[J]. 计算机应用, 2011, 31(7): 1804-1807. Ouyang Zhe and Zhou Yong-quan. Self-adaptive step glowworm swarm optimization algorithm[J]. Journal of Computer Applications, 2011, 31(7): 1804-1807. (  1) 1) |
| [8] | 王凌, 李国林, 谢鑫, 等. 非圆信号二维DOA和初始相位联合 估计方法[J]. 雷达学报, 2012, 1(1): 43-49. Wang Ling, Li Guo-lin, Xie Xin, et al.. Joint 2-D DOA and noncircularity phase estimation method[J]. Journal of Radars, 2012, 1(1): 43-49. (  1) 1) |
| [9] | 张瑜, 李玲玲. 低角雷达跟踪时的多路径散射模型[J]. 电波科 学学报, 2004, 19(1): 83-86. Zhang Yu and Li Ling-ling. Multipath scatting model of low angle radar tracking[J]. Chinese Journal of Radio Science, 2004, 19(1): 83-86. (  1) 1) |
| [10] | Krishnand K N and Ghose D. Detection of multiple source locations using a glowworm metaphor with applications to collective robotics[C]. Swarm Intelligence Symposium, Washington. D.C, USA, June 2005: 84-91.
( 1) 1) |
| [11] | 黄正新. 人工萤火虫群优化算法分析改进及应用研究[D]. [硕 士论文], 广西民族大学, 2011: 6-7. Huang Zheng-xin. Research on artificial Glowworm Swarm Optimization algorithm analysis improve and application[D]. [Master dissertation], Guangxi University for Nationalities, 2011: 6-7. (  1) 1) |
| [12] | 吴伟民, 亢少将, 林志毅, 等. 基于改进萤火虫算法的多模函数 优化[J]. 计算机应用与软件, 2014, 31(1): 283-285, 302. Wu Wei-min, Kang Shao-jiang, Lin Zhi-yi, et al.. Multimodal function optimization based on improved Glowworm Swarm Optimization[J]. Computer Applications and Software, 2014, 31(1): 283-285, 302. (  1) 1) |
| [13] | 李逦, 姚晔, 李铁. 基于改进型人工萤火虫算法的云计算资源 研究[J]. 计算机应用研究, 2013, 30(8): 2298-2300, 2333. Li Li, Yao Ye, and Li Tie. Study on improved artificial firefly algorithm in cloud computing resources[J]. Application Research of Computers, 2013, 30(8): 2298-2300, 2333. (  1) 1) |
| [14] | Krishnand K N and Ghose D. Glowworm swarm optimization for simultaneous capture of multiple local optima of multimodal functions[C]. Swarm Intelligence Symposium, Boston, USA, 2009: 87-124.
( 1) 1) |
| [15] | 张兴良, 王可人, 樊甫华. 典型阵列快速MUSIC算法研究[J]. 雷达学报, 2012, 1(2): 149-156. Zhang Xing-liang, Wang Ke-ren, and Fan Fu-hua. Study on fast MUSIC algorithm with typical array[J]. Journal of Radars, 2012, 1(2): 149-156. (  1) 1) |


