由于目标机动、长采样间隔、低探测率、系统和测量误差等原因,雷达对目标的跟踪轨迹常常发生中断,航迹中断对于信息融合会造成严重的干扰,因而中断航迹的配对关联是雷达数据处理领域亟需解决的关键问题之一。中断航迹的配对关联及连接问题早在上世纪80年代就被提出[1],最近几年已成为国内外学者的关注热点。文献[2]提出了基于统计加权的中断航迹关联(Track Segment Association,TSA)算法,为后续中断航迹关联方法的研究发展奠定了基础。该算法将新航迹后向预测至老航迹最后一个状态更新点,由新老航迹对该点作状态估计的马氏距离判断是否满足关联条件,并用2维分配方法处理多义性问题,文献[3, 4]基于上述方法及其改进算法解决了因目标停走机动造成的航迹中断关联问题;文献[5]将上述方法应用于解决弹道目标的中断航迹关联;文献[6]引入转弯模型对机动目标的中断航迹做状态预测。文献[7, 8, 9, 10]分别基于模糊关联理论和证据理论处理中断航迹关联问题,为该问题的研究提供了新思路。
TSA算法在理论上具有可行性,然而在实际情况下存在以下问题:(1)由于系统和测量噪声的存在,新航迹的后向预测常常误差较大,造成新老航迹基于单个点的关联配对准确性较差,导致误关联、漏关联经常发生;(2)当目标密集时,因航迹交叉、分岔经常发生错关联[11, 12],TSA算法性能骤然下降。
为有效克服预测误差对航迹匹配关联造成的影响,本文基于多目标多传感器统计双门限航迹关联理论,提出了基于统计双门限的中断航迹配对关联算法。全文内容安排如下,第2节阐述问题、提出有关概念并简要介绍粗关联,即速度匹配。第3节是全文的核心内容,包括关联样本提取及预处理、中断航迹配对关联准则、中断航迹关联的多义性及其解决办法—2维最优分配算法。第4节是仿真验证,体现出本文算法对于TSA算法的优越性能。第5节总结全文。
2 问题阐述及粗关联 2.1 问题阐述对中断前后航迹段进行配对关联,即判断中断前后的某对航迹段是否源自同一目标,首先定义中断前后的航迹片段。
(1) 老航迹:因缺少量测数据无法进行状态更新的中断航迹。
| ${{\mathbf{T}}^{i}}=\left\{ {{\widehat{\mathbf{x}}}^{i}}\left( k|k \right),k=k_{s}^{i},\cdots ,k_{e}^{i} \right\}, i=1,2,\cdots ,I$ | (1) |
(2) 新航迹:新起始的航迹段,可能是因各种原因中断的“老航迹”的继续。
| ${{\mathbf{T}}^{j}}=\left\{ {{\widehat{\mathbf{x}}}^{j}}\left( k|k \right),k=k_{s}^{j},\cdots ,k_{e}^{j} \right\}, j=1,2,\cdots ,J$ | (2) |
定义I行J列的航迹段关联矩阵,
| $\Pi =\left( \begin{matrix} \begin{matrix} {{\pi }_{11}} & {{\pi }_{12}} \\ {{\pi }_{21}} & {{\pi }_{22}} \\ \end{matrix} & \begin{matrix} \cdots & {{\pi }_{1J}} \\ \cdots & {{\pi }_{2J}} \\ \end{matrix} \\ \begin{matrix} \vdots & \vdots \\ {{\pi }_{I1}} & {{\pi }_{I2}} \\ \end{matrix} & \begin{matrix} \ddots & \vdots \\ \cdots & {{\pi }_{IJ}} \\ \end{matrix} \\ \end{matrix} \right)$ | (3) |
假设老航迹${{\mathbf{T}}^{i}}$和新航迹${{\mathbf{T}}^{j}}$是同一目标一条航迹上中断的前后两条航迹段,则${{\mathbf{T}}^{i}}$和${{\mathbf{T}}^{j}}$在速度上满足匹配关系,即中断距离与中断时间之比小于目标的最大运动速度。对每条老航迹滤波后的最后一个状态更新点和每条新航迹做反向滤波后的最后一个状态更新点做速度匹配检测,满足速度匹配要求的${{\mathbf{T}}^{i}}$和${{\mathbf{T}}^{j}}$,则赋给${{\pi }_{ij}}=1$,否则排除${{\mathbf{T}}^{i}}$和${{\mathbf{T}}^{j}}$的关联可能,即${{\pi }_{ij}}=0$。
| ${{\Phi }_{v}}=\left\{ \left( {{\mathbf{T}}^{i}},{{\mathbf{T}}^{j}} \right):\begin{matrix} \frac{\left| {{\widehat{\xi }}^{j}}\left( k_{s}^{j}\text{ }|\text{ }k_{s}^{j} \right)-{{\widehat{\xi }}^{i}}\left( k_{e}^{i}\text{ }|\text{ }k_{e}^{i} \right) \right|}{t_{s}^{j}-t_{e}^{i}}<{{v}_{\text{max}}} \\ \frac{\left| {{\widehat{\eta }}^{j}}\left( k_{s}^{j}\text{ } |\text{ }k_{s}^{j} \right)-{{\widehat{\eta }}^{i}}\left( k_{e}^{i}\text{ }|\text{ }k_{e}^{i} \right) \right|}{t_{s}^{j}-t_{e}^{i}}<{{v}_{\text{max}}} \\ \frac{\left| {{\widehat{\varsigma }}^{j}}\left( k_{s}^{j}\text{ }|\text{ }k_{s}^{j} \right)-{{\widehat{\varsigma }}^{i}}\left( k_{e}^{i}\text{ }|\text{ }k_{e}^{i} \right) \right|}{t_{s}^{j}-t_{e}^{i}}<{{v}_{\text{max}}} \\ \end{matrix} \right\}$ | (4) |
文献[2]提出的TSA算法将新航迹逆向预测至老航迹的最后一个状态更新点,只判断单个点马氏距离是否小于阈值即判决新老航迹段是否关联,这种方法可能因系统噪声、量测噪声、目标机动等因素影响关联效果,尤其目标密集环境下性能很差。本文提出基于统计双门限的中断航迹配对关联算法,将单点判断改为多点判断,选取长度为$R$的关联时段$\left\{ k_{s}^{a},\cdots ,k_{e}^{a} \right\}$的状态预测组成关联样本,对关联样本逐个基于${{\chi }^{2}}$分布门限进行假设检验,即第1门限判断,将满足第1门限的状态样本的个数与第2门限比较,判断该对新老航迹是否满足关联条件。
3.1 航迹跟踪预测及关联样本的提取对新航迹${{\mathbf{T}}^{j}}$由航迹终点$k_{e}^{j}$至起点$k_{s}^{j}$方向做逆向滤波,此时时间间隔是负值。滤波至选定的关联时刻$k_{e}^{a}$,注意这里可能$k_{e}^{a}>k_{s}^{j}$,即关联时刻选在新航迹起始后;或$k_{e}^{i}<k_{e}^{a}<k_{s}^{j}$,表示关联时刻选在中断区间内;如果$k_{e}^{i}>k_{e}^{a}$,表示关联时刻选在老航迹结束前。将新航迹逆向预测得到的以$k_{e}^{a}$时刻为终点的连续$R$个时刻的状态估计及其误差协方差估计分别作为长度为$R$的关联样本,
| $\begin{align} & {{\widehat{\mathbf{X}}}^{j}}\left( m \right)={{\widehat{\mathbf{x}}}^{j}}\left( k_{e}^{a}-R+m\left| {{\mathbf{T}}^{j}} \right. \right) \\ & \qquad \ \ \ \ \ ={{\widehat{\mathbf{x}}}^{j}}\left( k_{s}^{a}-1+m\left| {{\mathbf{T}}^{j}} \right. \right), \\ & \qquad \qquad \quad m=1,2,\cdots ,R \\ \end{align}$ | (5) |
| $\begin{align} & {{\mathbf{P}}^{j}}\left( m \right)={{\mathbf{p}}^{j}}\left( k_{e}^{a}-R+m\left| {{\mathbf{T}}^{j}} \right. \right) \\ & \qquad \quad ={{\mathbf{p}}^{j}}\left( k_{s}^{a}-1+m\left| {{\mathbf{T}}^{j}} \right. \right), \\ & \qquad \qquad \ m=1,2,\cdots ,R \\ \end{align}$ | (6) |
将老航迹${{\mathbf{T}}^{i}}$正向滤波得到的以关联时刻$k_{s}^{a}$为起点的连续$R$个时刻的状态估计和误差协方差估计作为长度为$R$的关联样本。
| $\begin{align} & {{\widehat{\mathbf{X}}}^{i}}\left( m \right)={{\widehat{\mathbf{x}}}^{i}}\left( k_{s}^{a}-1+m\left| {{\mathbf{T}}^{i}} \right. \right), \\ & \qquad \qquad \ \ m=1,2,\cdots ,R \\ \end{align}$ | (7) |
| $\begin{align} & {{\mathbf{P}}^{i}}\left( m \right)={{\mathbf{p}}^{i}}\left( k_{s}^{a}-1+m\left| {{\mathbf{T}}^{i}} \right. \right), \\ & \qquad \qquad \ \ m=1,2,\cdots ,R \\ \end{align}$ | (8) |
定义老航迹${{\mathbf{T}}^{i}}$和新航迹${{\mathbf{T}}^{j}}$的估计误差
| ${{\Delta }_{ij}}(n)={{\widehat{\mathbf{X}}}^{i}}(n)-{{\widehat{\mathbf{X}}}^{j}}(n)$ | (9) |
引入假设检验的思想,${{H}_{0}}$和${{H}_{1}}$分别表示事件的原假设和备择假设:
${{H}_{0}}$$\frac{\text{ }}{{}}$${{\widehat{\mathbf{X}}}^{i}}(n)$和是同一目标的新老航迹对目标同一时刻的状态估计;
${{H}_{1}}$$\frac{\text{ }}{{}}$${{\widehat{\mathbf{X}}}^{i}}(n)$和${{\widehat{\mathbf{X}}}^{j}}(n)$不是源自同一个目标。
由文献[2]可知,基于不同时刻的量测信息对同一目标同一时刻的状态估计误差统计独立,在${{\widehat{\mathbf{X}}}^{j}}(n)$假设下式(9)的协方差为:
| ${{\mathbf{P}}^{ij}}(n)={{\mathbf{P}}^{i}}(n)+{{\mathbf{P}}^{j}}(n)$ | (10) |
对于$n=1,2,\cdots ,R$,使用检验统计量
| ${{\alpha }_{ij}}(n)={{\left[ {{\Delta }_{ij}}(n) \right]}^{\prime }}{{\left[ {{\mathbf{P}}^{ij}}(n) \right]}^{-1}}\left[ {{\Delta }_{ij}}(n) \right]$ | (11) |
在${{H}_{0}}$假设中,状态估计误差${{\Delta }_{ij}}(n)$服从高斯分布,由文献[13]引理7.4可得,检验统计量${{\alpha }_{ij}}(n)$服从${{n}_{x}}$自由度的${{\chi }^{2}}$分布,${{n}_{x}}$是状态向量的维数。所以满足式(12)的一组样本点即满足中断航迹关联准则的第1门限。
| $\begin{align} & {{\alpha }_{ij}}\left( n \right)={{\left[ {{\Delta }_{ij}}(n) \right]}^{\prime }}{{\left[ {{\mathbf{P}}^{ij}}(n) \right]}^{-1}}\left[ {{\Delta }_{ij}}(n) \right] \\ & \qquad \quad \le \chi _{{{n}_{x}}}^{2}\left( 1-Q \right) \end{align}$ | (12) |
所谓统计双门限准则[11, 12],是对于长度为$R$的状态样本逐个进行第1门限检验,即${{\chi }^{2}}$分布检验,若判断某个状态样本接受${{H}_{0}}$,则计数器$\iota $加1,否则计数器值不变。经过$R$次${{\chi }^{2}}$检验后,将计数器$\iota $与第2门限$L$比较,如果$\iota \text{}L$,即$R$个样本中满足第1门限的样本数大于第2门限$L$,则判决老航迹${{\mathbf{T}}^{i}}$和新航迹${{\mathbf{T}}^{j}}$关联,即它们源自同一目标,否则判决${{\mathbf{T}}^{i}}$和${{\mathbf{T}}^{j}}$不关联。
对满足速度匹配的新老航迹逐对做统计双门限航迹段关联判决,有满足双门限的老航迹${{\mathbf{T}}^{i}}$和新航迹${{\mathbf{T}}^{j}}$,将关联矩阵中的元素${{\pi }_{ij}}$赋值1,对于不满足双门限的新老航迹,将关联矩阵中的元素${{\pi }_{ij}}$赋值0。
3.3 航迹质量设计在统计双门限航迹段关联准则中,我们定义航迹脱离质量${{D}_{ij}}(n)$,表示总数为$R$的样本检测进行完第$n$个时,被判定为不满足第1门限的样本点的个数。对于给定的样本总数$R$、第2门限$L$,如果在进行完第$n$个样本判决时,
| ${{D}_{ij}}(n)>R-L$ | (13) |
进行完上述关联判决之后,可能存在这样的情况,即某段老航迹${{\mathbf{T}}^{{{i}_{3}}}}$同时和两段新航迹${{\mathbf{T}}^{{{j}_{3}}}},$${{\mathbf{T}}^{{{j}_{4}}}}$满足双门限准则,即
| ${{\pi }_{{{i}_{3}}{{j}_{3}}}}={{\pi }_{{{i}_{3}}{{j}_{4}}}}=1$ |
| ${{\pi }_{{{i}_{5}}{{j}_{5}}}}={{\pi }_{{{i}_{6}}{{j}_{5}}}}=1$ |
要完成最优分配,首先要定义代价函数,使代价函数的加权和取值最小的分配方式即最优分配方式。本文使用统计双门限中断航迹关联判别方法,对长度为$R$的关联样本逐个进行${{\chi }^{2}}$检验,得出长度为$R$的代价向量$\mathbf{c}\left( i,j,n \right)$。
估计误差${{\Delta }_{ij}}(n)$的似然函数
| $\begin{align} & f\left[ {{\Delta }_{ij}}(n) \right]={{(2\pi )}^{-\frac{{{n}_{x}}}{2}}}{{\left| {{\mathbf{P}}^{ij}}(n) \right|}^{-\frac{1}{2}}} \\ & \qquad \qquad \quad \cdot \exp \left\{ -\frac{1}{2}{{\left[ {{\Delta }_{ij}}(n) \right]}^{\prime }}{{\left[ {{\mathbf{P}}^{ij}}(n) \right]}^{-1}}\left[ {{\Delta }_{ij}}(n) \right] \right\} \\ \end{align}$ | (14) |
| $\mathbf{c}\left( i,j,n \right)\text{=}\left\{ \begin{align} & \frac{{{\left[ {{\Delta }_{ij}}(n) \right]}^{\prime }}{{\left[ {{\mathbf{P}}^{ij}}(n) \right]}^{-1}}\left[ {{\Delta }_{ij}}(n) \right]}{2}+\ln \left( {{\left| {{\mathbf{P}}^{ij}}(n) \right|}^{\frac{1}{2}}} \right), \\ & \quad \ \ 老航迹{{\mathbf{T}}^{i}}和新航迹{{\mathbf{T}}^{j}}匹配 \\ & \infty , 老航迹{{\mathbf{T}}^{i}}和新航迹{{\mathbf{T}}^{j}}不匹配 \\ \end{align} \right.$ | (15) |
对代价向量中满足第1门限的样本代价值取均值作为老航迹${{\mathbf{T}}^{i}}$和新航迹${{\mathbf{T}}^{j}}$的分配代价
| $\mathbf{c}\left( i,j \right)=\frac{\sum\limits_{n=1}^{\iota }{\mathbf{c}\left( i,j,n \right)}}{\iota }$ | (16) |
文献[2]使用的2维最优分配用于解决中断航迹关联的多义性问题,2维最优分配可以统筹所有新老航迹,选出全局加权代价最小的航迹关联组合。2维分配变量$\mathbf{a}\left( i,j \right)$的取值应该使分配代价的加权和最小,
| $\underset{a}{\mathop{\min }}\,\underset{i=1}{\overset{I}{\mathop \sum }}\,\underset{j=1}{\overset{J}{\mathop \sum }}\,\mathbf{c}\left( i,j \right)\mathbf{a}\left( i,j \right)$ | (17) |
| $\underset{i=1}{\overset{I}{\mathop \sum }}\,\mathbf{a}\left( i,j \right)=1, j=1,2,\cdots ,J$ | (18) |
| $\underset{j=1}{\overset{J}{\mathop \sum }}\,\mathbf{a}\left( i,j \right)=1, i=1,2,\cdots ,I$ | (19) |
| $\mathbf{a}\left( i,j \right)=\left\{ \begin{align} & 1, {{T}^{i}}{{T}^{j}} \\ & 0, {{T}^{i}}{{T}^{j}} \\ \end{align} \right.$ | (20) |
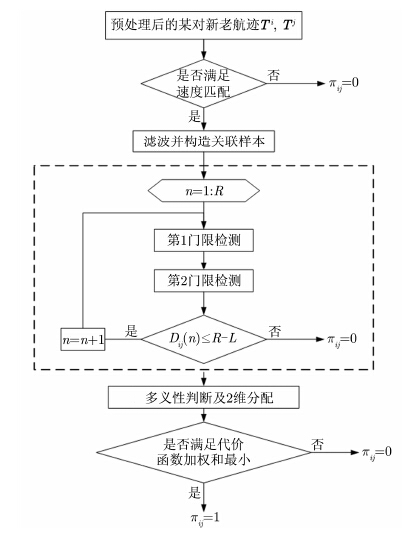
|
图 1 算法流程示意图 Fig.1 Flow chart of the algorithm |
为验证本文提出算法的有效性,设计了空中飞行目标和弹道目标两种仿真环境,在相同条件下分别比较本文算法与TSA算法的关联效果。
这里需要定义中断航迹配对关联的几个评价指标,
| ${{R}_{ga}}=\frac{m}{M}$ | (21) |
| ${{R}_{ta}}=\frac{{{n}_{t}}}{n}$ | (22) |
| ${{R}_{fa}}\text{=}\frac{{{n}_{f}}}{n}$ | (23) |
| ${{R}_{na}}\text{=}\frac{{{n}_{n}}}{n}$ | (24) |
飞行器在指定空域匀速等高飞行,雷达受到干扰造成部分量测数据丢失,导致航迹中断。雷达量测噪声服从均值为零的高斯分布,其中测距误差标准差${{\sigma }_{r}}=$50 m,测角误差标准差${{\sigma }_{\theta }}=0.5{}^\circ $,采样间隔$T=$1 s。目标起始时刻状态分别为[-12000,226,-200,10][-12000,226,-800,26][-12000,226,-1500,40],中断时间内航迹交叉,飞行时间100 s,航迹中断发生在40~50 s。使用状态向量维数为4的匀速直线运动卡尔曼滤波模型做目标跟踪及新航迹后向预测,具体算法参考文献[14]。
分别使用TSA算法和本文算法对飞行器中断航迹做配对关联,关联样本长度$R=10$,第2门限$L=6$。利用以上环境做200次蒙特卡洛仿真,其中一次仿真场景及关联效果如图 2-图 4所示,比较TSA算法与本文算法的关联效果。如图 3所示,TSA算法将航迹预测至某个关联时刻作距离判断,由于滤波误差的影响航迹段关联判断错误,本文算法增加了关联样本的长度,能更准确地描述目标的运动走势,有效地克服了误差对关联结果的影响。
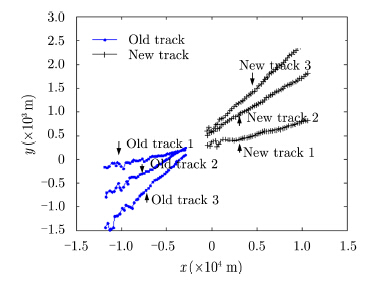
|
图 2 空中飞行目标环境航迹中断 Fig.2 Track segments of air targets |
为研究关联样本的长度对关联效果的影响,分别设置$R=5,$$L=3$和$R=10,$$L=6$两种仿真场景,比较统计双门限航迹关联算法同TSA算法的性能。仿真场景中各目标关联正确的次数如表 1所示,全局关联正确率、平均正确关联率、平均错误关联率、平均漏关联率如表 2所示。
| 表 1 空中飞行目标环境目标关联正确次数 Tab. 1 Correct association time in air targets environment |
| 表 2 空中飞行目标环境关联评价参数(%) Tab. 2 Association parameters in air targets environment (%) |
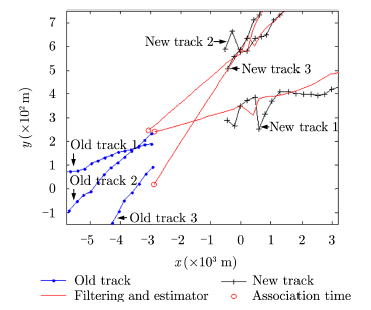
|
图 3 空中飞行目标环境TSA算法关联效果 Fig.3 TSA results in air targets environment |
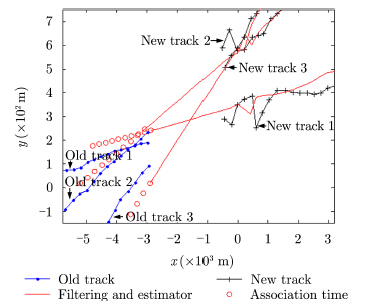
|
图 4 空中飞行目标环境本文算法关联效果 Fig.4 Modified algorithm results in air targets environment |
仿真实验结果显示,当$R=5,$$L=3$时,本文算法将TSA算法的平均正确关联率提升了8%,将平均漏关联率降低了10.4%;$R=10,$$L=3$时,本文算法将TSA算法的平均正确关联率提升了14.3%,将平均漏关联率降低了14.7%。仿真结果表明,在空中飞行目标场景下,本文算法的关联效果比TSA算法有较大幅度的提高,验证了本文算法对于因随机误差、目标密集、航迹交叉或分岔引起的航迹跟踪和预测误差具有更强的适应性。
比较不同关联样本和第2门限条件下的统计双门限航迹关联算法的性能可知,当关联样本和第2门限长度增大时,200次蒙特卡洛仿真中各目标的正确关联次数、算法平均正确关联率均有明显增长,漏关联率降低。考虑统计双门限中断航迹关联算法原理及本文使用的匀速直线运动模型,当关联样本长度增大时,算法具有更强的克服随机误差的能力,关联效果随之提高。
4.2 弹道目标仿真场景本文从文献[5]得到启发,建立密集的弹道目标中断航迹仿真环境,验证本文算法对于中断航迹配对关联具有的优越性能。
弹道目标起始位置在空间直角坐标系([-1000,1000],232000,[87500, 88500])(单位m)区域内平均分布,个数为10个,雷达测距误差标准差${{\sigma }_{r}}=$500 m,方位角和俯仰角的测角误差标准差均为0.1 mrad,服从均值为零的正态分布。采样间隔为$T=$2 s,目标运行时间0~100 s,中断时间发生在40~50 s。
弹道目标在再入段飞行主要受到地球引力和空气阻力的作用,这里忽略离心加速度、科里奥利加速度、风力、弹头牵引力及目标自身旋转对于运动状态的影响,为简化运算,做小范围内地球表面是平面的假设。参考文献[15],目标状态转换方程如式(25)所示:
| $\mathbf{X}\left( k+1 \right)=\mathbf{FX}\left( k \right)+\mathbf{Gf}\left( \mathbf{X}\left( k \right) \right)+\mathbf{G}\left[ \begin{matrix} 0 \\ -g \\ \end{matrix} \right]$ | (25) |
| $\mathbf{X}\left( k \right)\triangleq {{\left[ {{x}_{k}}~ {{{\dot{x}}}_{k}} {{y}_{k}} {{{\dot{y}}}_{k}} {{z}_{k}} {{{\dot{z}}}_{k}} \right]}^{\text{T}}}$ | (26) |
| $\mathbf{F}\triangleq \left[ \begin{matrix} \begin{matrix} 1 & T & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{matrix} & \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ T & 0 & 0 \\ \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{matrix} & \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & T \\ 0 & 0 & 1 \\ \end{matrix} \\ \end{matrix} \right]$ | (27) |
| $\mathbf{G}\triangleq \left[ \begin{matrix} 0 0 \\ 0 0 \\ \frac{{{T}^{2}}}{2} 0 \\ T \text{0} \\ \text{0} \frac{{{T}^{2}}}{2} \\ \text{0} T \\ \end{matrix} \right]$ | (28) |
| $\mathbf{f}\left( \mathbf{X}\left( k \right) \right)=-0.5\frac{g}{\beta }\rho \left( {{z}_{k}} \right)\sqrt{\dot{y}_{k}^{2}+\dot{z}_{k}^{2}}\left( \begin{matrix} {{{\dot{y}}}_{k}} \\ {{{\dot{z}}}_{k}} \\ \end{matrix} \right)$ | (29) |
量测转换方程如式(30)所示:
| $\mathbf{Z}\left( k+1 \right)=\mathbf{HX}\left( k+1 \right)+\mathbf{W}\left( k+1 \right)$ | (30) |
| $\mathbf{H}\triangleq \left[ \begin{matrix} \begin{matrix} \begin{matrix} 1 & 0 \\ \end{matrix} \\ \begin{matrix} 0 & 0 \\ \end{matrix} \\ \begin{matrix} 0 & 0 \\ \end{matrix} \\ \end{matrix} & \begin{matrix} \begin{matrix} 0 & 0 \\ \end{matrix} \\ \begin{matrix} 1 & 0 \\ \end{matrix} \\ \begin{matrix} 0 & 0 \\ \end{matrix} \\ \end{matrix} & \begin{matrix} \begin{matrix} 0 & 0 \\ \end{matrix} \\ \begin{matrix} 0 & 0 \\ \end{matrix} \\ \begin{matrix} 1 & 0 \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \right]$ | (31) |
采用容积卡尔曼滤波算法[16, 17]对目标做非线性跟踪及状态预测,选择新航迹起始后的第3个量测时刻作为关联时段的起始,令。对上述场景做200次蒙特卡罗仿真,其中一次仿真场景及关联结果如图 5-图 7所示,统计TSA算法和本文算法的关联结果如表 3所示。
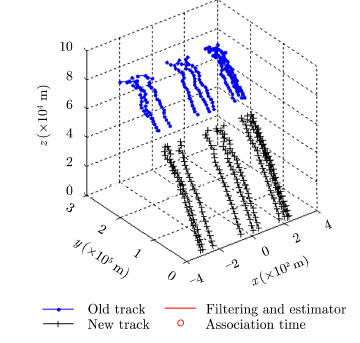
|
图 5 弹道目标环境航迹中断 Fig.5 Track segments of ballistic targets |
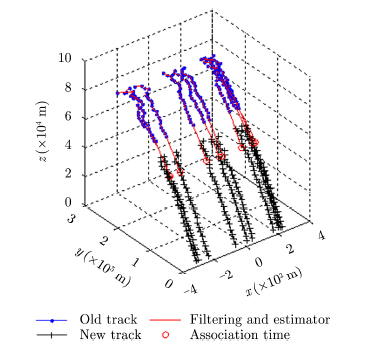
|
图 6 弹道目标环境TSA算法关联效果 Fig.6 TSA results in ballistic targets environment |
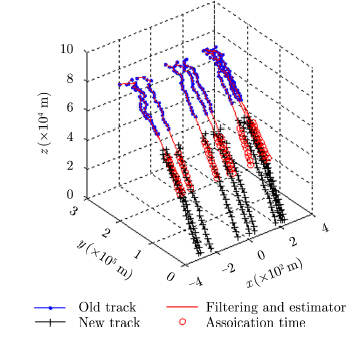
|
图 7 弹道目标环境本文算法关联效果 Fig.7 Modified algorithm results in ballistic targets environment |
| 表 3 弹道环境1关联评价参数(%) Tab. 3 Ballistic environment 1 association parameters (%) |
令弹道目标起始位置在空间直角坐标系([-500,500],232000,[87500, 88500])(单位m)区域内平均分布,增加$R=5,$$L=3$仿真条件,关联结果如表 4所示。
| 表 4 弹道环境2关联评价参数(%) Tab. 4 Ballistic environment 2 association parameters (%) |
仿真实验结果显示,在弹道环境1条件下,本文算法将TSA算法的全局正确关联率提升了22%,平均正确关联率提升了21.5%,将平均漏关联率降低了21.35%,平均错误关联率基本不变;当目标起始位置在空间直角坐标系([-500,500],232000,[87500, 88500]) (单位m)区域内平均分布,目标密集程度增加,本文算法将TSA算法的全局正确关联率提升了23.5%,平均正确关联率提升了21.8%,将平均漏关联率降低了21.8%,平均错误关联率基本不变。仿真结果表明,在弹道目标场景下,本文算法的关联效果比TSA算法有较大幅度的提高,验证了本文算法在复杂环境下对中断航迹配对关联具有更高的关联正确率和更低的漏关联率。
分析表 4中$R=5,$$L=6$和$R=10,$$L=3$两种仿真条件下的实验结果可知,在弹道目标场景下,基于统计双门限的中断航迹配对关联算法在关联样本长度降低时,关联效果受到的影响较小。综合分析空中飞行目标场景和弹道目标场景下关联样本长度对关联性能产生的影响可知,不同的运动状态和误差条件下,关联样本长短对关联效果造成的影响不一致。具体地说,当关联样本取值较长时(取值10),航迹预测长度也相应地增长,预测误差增大,关联准确性降低;当关联样本取值较短时(取值5),因随机误差的影响,关联样本可能无法准确描述目标的运动状态,造成关联不准确。因具体环境下目标运动模型、随机误差及中断时间长短等因素均对中断航迹关联判决产生影响,关联样本和第2门限的取值方法要根据具体应用环境设置。
5 结论(1) 经仿真验证,在空中飞行目标和弹道目标密集场景下,本文算法的全局正确关联率和平均正确关联率均比TSA算法有显著提高,漏关联率显著下降,表明了本文算法对于航迹预测误差具有更强的适应性,较经典的TSA算法具有更强的关联性能。本文算法在多目标雷达数据处理中对于提高航迹寿命,改善跟踪效果具有较大的参考价值。
(2) 本文设置的关联样本长度分别为5和10,经仿真比较可知,空中飞行目标仿真环境和弹道目标仿真环境下,关联样本长度对关联性能产生的影响不同。具体应用环境下,关联样本长度与关联性能的关系还会受到目标运动模型、随机噪声的大小、中断时间长短等因素的影响。
(3) 文中粗关联部分使用的速度门限检测方法在空中飞行目标和弹道目标场景下具有快速滤除非关联航迹对的能力,在海面慢速目标场景下,由于速度估计不准确,可考虑转弯率门限检测或加速度门限检测。在其它应用背景下,也可考虑基于其它目标属性的简单有效的粗关联方法。
(4) 本文算法适用于目标运动模型较稳定的情况,如文中举例的弹道目标运动场景。当目标发生大机动时,基于航迹预测的中断航迹配对关联算法由于无法准确描述中断区间的机动运动,关联效果恶化严重。关于机动目标的中断航迹关联是下一步研究的重点。
| [1] | Mucci R, Arnold J, and Bar-Shalom Y. Track segment association with a distributed field of sensors[J]. Acoustical Society of America, 1985, 78(4): 1317-1324.( 1) 1) |
| [2] | Yeom S W, Kirubarajan T, and Bar-Shalom Y. Track segment association, fine-step IMM and initialization with Doppler for improved track performance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(1): 293-309.( 4) 4) |
| [3] | Zhang S and Bar-Shalom Y. Track segment association for GMTI tracks of Evasive Move-Stop-Move maneuvering targets[J]. IEEE Transactions on Aerospace and Electronic System, 2011, 47(3): 1899-1914.( 1) 1) |
| [4] | Pannetier B and Dezert J. Track segment association with classification information[C]. 2012 Workshop on Sensor Data Fusion: Trends, Solution, Applications (SDF), Bonn, Germany, 2012: 60-65.( 1) 1) |
| [5] | 俞建国, 刘梅, 陈锦海. 弹道目标航迹片段关联及优化[J]. 航空学报, 2011, 32(10): 1897-1904. Yu Jian-guo, Liu Mei, and Chen Jin-hai. Ballistic target track segments association and optimization[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10): 1894-1904.(  2) 2) |
| [6] | Zhang Wei, Liang Yan, Lan Hua, et al.. Track segments association for maneuver targets[J]. Computer & Digital Engineering, 2013, 41(3): 394-398.( 1) 1) |
| [7] | 杜渐, 夏学知. 一种面向信号中断的航迹关联算法[C]. 第四届中国信息融合大会, 武汉, 2012: 518-522. Du Jian and Xia Xue-zhi. A fuzzy track association algorithm in track interrupt-oriented[C]. The 4th National Conference on Information Fusion, Wuhan, 2012: 518-522.(  1) 1) |
| [8] | 杜渐, 夏学知. 面向航迹中断的模糊航迹关联算法[J]. 火力指挥与控制, 2013, 38(6): 68-71. Du Jian and Xia Xue-zhi. A fuzzy track association algorithm in track interrupt-oriented[J]. Fire Control & Command Control, 2013, 38(6): 68-71.(  1) 1) |
| [9] | 高岚, 江晶, 蓝江桥. 基于DSmT 的机载目标断续航迹关联[J]. 传感器与微系统, 2012, 31(4): 26-32. Gao Lan, Jiang Jing, and Lan Jiang-qiao. Association of airborne target broken tracks based on DSmT[J]. Transducer and Microsystem Technologies, 2012, 31(4): 26-32.(  1) 1) |
| [10] | 郭振, 兰华, 关超, 等. 一种基于证据推理的断裂航迹粘连方 法[C]. 第五届中国信息融合大会, 深圳, 2013: 53-60. Guo Zhen, Lan Hua, Guan Chao, et al.. Track segment association based on Dempster-Shafer evidence theory[C]. The 5th National Conference on Information Fusion, Shenzhen, 2013: 53-60.(  1) 1) |
| [11] | 何友, 王国宏, 陆大, 等. 多传感器信息融合及应用[M]. 第2版, 北京: 电子工业出版社, 2007: 136-141. He You, Wang Guo-hong, Lu Da-jin, et al.. Multisensor Information Fusion With Applications[M]. 2nd Edition, Beijing: Publishing House of Electronics Industry, 2007: 136-141.(  2) 2) |
| [12] | 何友, 王国宏, 关欣. 信息融合理论与应用[M]. 北京: 电子工业出版社, 2010: 189-193. He You, Wang Guo-hong, and Guan Xin. Information Fusion Theory with Applications[M]. Beijing: Publishing House of Electronics Industry, 2010: 189-193.(  2) 2) |
| [13] | 吴翊, 李永乐, 胡庆军. 应用数理统计[M]. 长沙: 国防科技大学出版社, 1995: 265-285. Wu Yi, Li Yong-le, and Hu Qing-jun. Applied Mathematical Statistics[M]. Changsha: Publishing House of National University of Defense Technology, 1995: 265-285.(  1) 1) |
| [14] | 何友, 修建娟, 关欣. 雷达数据处理及应用[M]. 第3 版, 北京: 电子工业出版社, 2013: 36-62. He You, Xiu Jian-juan, and Guan Xin. Radar Data Processing with Applications[M]. 3rd Edition, Bejing: Publishing House of Electronics Industry, 2013: 36-62.(  1) 1) |
| [15] | Farina A, Ristic B, and Benvenuti D. Tracking a ballistic target: comparison of several nonlinear filters[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 854-867.( 1) 1) |
| [16] | Arasaratnam I and Haykin S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.( 1) 1) |
| [17] | Arasaratnam I and Haykin S. Cubature Kalman smoothers[J]. Automatica, 2011, 47(10): 2245-2250.( 1) 1) |


