②72495 部队通信科 郑州 450001
②Automation Station, Unit 72495, Zhengzhou 450001, China
作为阵列信号处理的研究热点和难点之一,宽带波束形成已广泛应用于通信、声呐、雷达以及地震勘探等众多国民经济领域[1,2,3]。两种最基本的FIR波束形成器分别为Frost波束形成器[4]和广义旁瓣对消(Generalized Sidelobe Canceller,GSC)波束形成器[5]。它们在每个阵元后面连接预延迟补偿和一组抽头延迟线(Tapped Delay-Lines,TDL),以更好地抑制干扰和随机噪声。
随着处理带宽越来越宽,FIR宽带波束形成方法需要较长长度的抽头延迟线以获取期望的输出信干噪比(Signal to Interference-plus-Noise Ratio,SINR)[6],但大量的抽头延迟线组将降低自适应权系数求解的收敛速度、增加计算复杂度。为此,文献[7]利用波束空间技术以提高算法的收敛速度,但波束空间的主波束和副波束的设计需要较大的计算量。文献[8]基于子带滤波器设计,利用子带宽带波束形成技术提高了收敛速度,降低了计算量,但子带滤波器设计复杂且重构误差对输出性能影响较大。文献[9]在GSC结构中引入频率不变约束,降低了计算量,但文献[7, 8, 9]均没有减少权系数的维数。为了大幅减少权系数的维数,文献[10]首次提出利用IIR滤波器代替宽带波束形成器中的FIR滤波器,在GSC结构下给出3种IIR宽带波束形成器,并证明了同等条件下IIR宽带波束形成器的性能优于FIR滤波器。文献[11]通过理想滤波器去极点的设计来降低IIR滤波器的阶数。文献[12]将IIR滤波器与FIR扇形滤波器相结合,有效地应用于部分自适应阵列中。文献[13]提出基于TDL形式的IIR宽带波束形成算法,该算法在每个阵元上连接预延迟补偿和一组类TDL形式的IIR滤波器,并结合约束和无约束最小均方误差(LMS)算法求解最优权系数矢量。基于文献[13],文献[14]进一步给出了2阶IIR单元下的宽带波束形成和GSC结构下新的IIR宽带波束形成器,提高了算法的收敛速度。文献[10, 11, 12, 13, 14]提出的IIR宽带波束形成器输出SINR较高且抗干扰性能较好,但IIR滤波器需要进行多极点的自适应调整,稳定性得不到保证。为此,文献[15]提出了一种基于Laguerre滤波器的类TDL形式宽带波束形成器[15]。与传统IIR滤波器相比,Laguerre滤波器既保持了FIR滤波器的稳定性,又具有IIR滤波器较长的记忆深度。另外,Laguerre宽带波束形成器仅需求解一个单极点,避免了多极点的自适应调整过程,保证了算法的稳定性,但单极点的求解仍较复杂,且该算法的收敛速度较慢。
本文将Laguerre滤波器引入GSC模型中,构建GSC结构下Laguerre宽带波束形成器模型,在无约束自适应求解的条件下提出一种低复杂度的Laguerre滤波器极点选取方法,然后利用归一化最小均方根误差方法实现宽带波束形成,最后给出了仿真实验与结果分析。
2 模型传统的基于GSC的IIR宽带波束形成器的结构如图 1(a) 所示,wq为静态权矢量,B表示阻塞矩阵。假设P个远场宽带信号以方位角θ入射到一均匀直线阵,阵元数为M,每个阵元均连接预延迟补偿T。则阵列输出误差$e(n)$表示为:
| $e(n)=d(n)-\left( \frac{1}{1+{{z}^{-1}}A(z)} \right)\sum\limits_{i=1}^{M-1}{{{H}_{i}}(z){{x}_{i}}(n)}$ | (1) |

|
图 1 宽带波束形成结构图 Fig.1 Wideband beamformer structure |
由文献[15]可知,Laguerre函数通常可以定义为:
| ${{L}_{k}}(z,b)=\sqrt{1-{{b}^{2}}}\frac{{{\left( {{z}^{-1}}-b \right)}^{k}}}{{{\left( 1-b{{z}^{-1}} \right)}^{k+1}}},k=0,1,2,\cdots $ | (2) |
| $H(z)=\sum\limits_{k=0}^{\infty }{{{\alpha }_{k}}(b){{L}_{k}}(z,b)}$ | (3) |
| ${{\alpha }_{k}}(b)=\left\langle H(z){{L}_{k}}(z,b) \right\rangle =\frac{1}{2\pi \text{j}}\oint_{C}{H(z){{L}_{k}}({{z}^{-1}},b)}{{z}^{-1}}\text{d}z$ | (4) |
为了实现宽带波束形成,假设目标滤波器${{H}_{\text{bp}}}\text{(}z)$为一个理想带通滤波器
| ${{H}_{\text{bp}}}(z)=\left\{ \begin{align} & {{z}^{-\tau }},{{\text{e}}^{\text{j}{{w}_{1}}}}<z<{{\text{e}}^{\text{j}{{w}_{2}}}},{{\text{e}}^{-\text{j}{{w}_{2}}}}<z<{{\text{e}}^{-\text{j}{{w}_{1}}}} \\ & 0, \\ \end{align} \right.$ | (5) |
| $\widehat{H}(z)=\sum\limits_{k=0}^{J}{{{\alpha }_{k}}(b){{L}_{k}}(z,b)}\approx {{H}_{\text{bp}}}(z)$ | (6) |
| $\varepsilon (b)=\frac{1}{2\pi }\int_{{}_{2\pi }}{{{\left| {{H}_{\text{bp}}}\left( {{\text{e}}^{\text{j}w}} \right)-\widehat{H}\left( {{\text{e}}^{\text{j}w}} \right) \right|}^{2}}\text{d}w}$ | (7) |
| $\varepsilon (b)=\frac{1}{2\pi }\int_{2\pi }{{{\left| {{H}_{\text{bp}}}\left( {{\text{e}}^{jw}} \right)-\sum\limits_{k=0}^{J}{{{\alpha }_{k}}(b){{L}_{k}}(z,b)} \right|}^{2}}\text{d}w}$ | (8) |
| $\begin{align} & \frac{\text{d}(\varepsilon (b))}{\text{d}b}=\sum\limits_{k=0}^{J}{{{\alpha }_{k}}(b)}-\frac{\text{d}({{\alpha }_{k}}(b))}{\text{d}b} \\ & =\frac{J+1}{1-{{b}^{2}}}{{\alpha }_{J}}(b){{\alpha }_{J+1}}(b)=0 \\ \end{align}$ | (9) |
由文献[10]可知,最优的单极点${{b}_{\text{opt}}}$是满足${{\alpha }_{J+1}}(b)=0$的一个解。但${{\alpha }_{J+1}}(b)=0$存在多个解,由文献[15]中的Laguerre-Frost算法需要利用搜索算法寻找使得误差$\varepsilon (b)$最小的解,即最优的单极点${{b}_{\text{opt}}}$,过程较为复杂,且收敛速度较慢。详细过程见文献[15],在此不再赘述。
3.2 本文算法GSC结构可以利用无约束的NLMS实现自适应,所以各支路Laguerre滤波器组的最优单极点可以是同一个最优值${{b}_{i}}={{b}_{j}},i,j=1,2,\cdots ,M-1$,也可以选择相互独立的不同的值${{b}_{i}}\ne {{b}_{j}}$。如果选择相互独立的最优单极点的值,则基于GSC的Laguerre宽带波束形成算法无需搜索式(9)的最优解,选择其所有解中满足$\left| b \right|<1$的值即可避免最优值的寻优过程,极大地减少了滤波器设计的复杂度。
为了减少计算复杂度,本文选取相互独立的极点,则信号$\widetilde{x}(n)$经Laguerre滤波器后可得
| $\left. \begin{align} & {{{\tilde{x}}}_{m,1}}(n)={{b}_{m}}{{{\tilde{x}}}_{m,1}}(n-1)+\sqrt{1-b_{m}^{2}}{{r}_{m}}(n) \\ & {{{\tilde{x}}}_{m,j}}(n)={{{\tilde{x}}}_{m,j-1}}(n-1)+{{b}_{m}}{{{\tilde{x}}}_{m,j}}(n-1)-{{b}_{m}}{{{\tilde{x}}}_{m,j-1}}(n) \\ & m=1,2,\cdots ,M-1,j=2,3,\cdots ,J \\ \end{align} \right\}$ | (10) |
由图 1(b)可知,GSC宽带波束形成器的最优权矢量w为:
| $w={{[{{w}_{1,1}} \cdots {{w}_{M-1,1}} \cdots {{w}_{1,J}} \cdots {{w}_{M-1,J}}]}^{\text{T}}}$ | (11) |
利用NLMS迭代求解最优权矢量w,则
| $y(n)=d(n)-{{w}^{\text{H}}}(n)\widetilde{x}(n)$ | (12) |
| $w\left( n+1 \right)=w(n)+\mu \frac{\widetilde{x}(n)}{{{\widetilde{x}}^{\text{H}}}(n)\widetilde{x}(n)}{{y}^{*}}(n)$ | (13) |
考虑一阵元数为12的均匀直线阵,选取Laguerre滤波器、IIR滤波器和FIR滤波器的阶数均为10,期望信号来向为$0{}^\circ $,两个干扰信号分别来自于$20{}^\circ $和$-45{}^\circ $。期望信号和干扰信号的最低频率${{f}_{l}}=800 \text{MHz}$,带宽为$B=400 \text{MHz}$,选取离散频率点数为15。阵元间距取期望信号最高频率对应波长的一半,信噪比为$10 \text{dB}$,信干比均为$-40 \text{dB}$,迭代次数为2000,迭代步长设为0.05,每次均做200次蒙特卡罗实验。
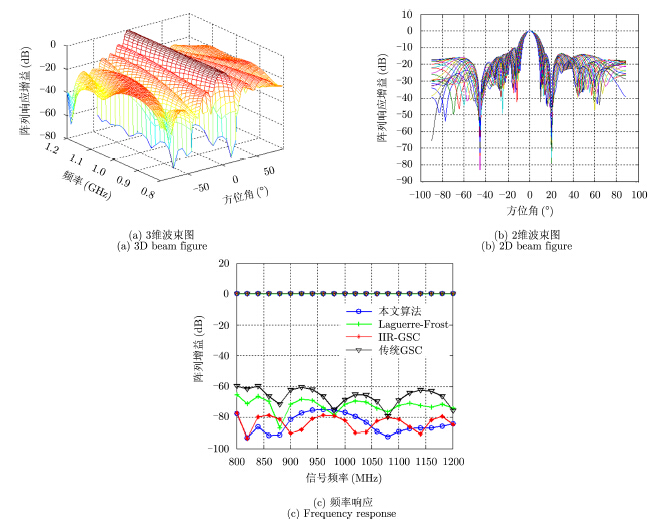
实验1 阵列响应性能
从图 2(a)和图 2(b)可以看出,本文算法波束主波束可以准确地指向期望信号方向,并在两个干扰方向上形成了很深的零陷。图 2(c)给出了本文算法、文献[15]中的基于Frost模型的Laguerre波束形成器(Laguerre-Frost)、文献[14]中基于GSC的IIR波束形成器(IIR-GSC)及传统GSC方法的期望信号0°及干扰信号20°在不同频率下阵列响应的变化。从图 2(c)中上面的4条曲线可以看出,4种算法在0°方向的阵列幅度响应均保持在0 dB左右,不同频率下的阵列幅度响应基本一致。图 2(c)在$-60 \text{dB}$以下的曲线代表了4种算法在干扰方向20°上形成的零陷。本文算法在方位角为20°的干扰方向上形成较深的零陷,与Laguerre-Frost方法和传统GSC方法相比,抗干扰性能有所提高。而IIR-GSC方法抗干扰性能较好,与本文算法性能相当,但IIR-GSC方法需要多极点的自适应调整过程和牛顿迭代方法,计算复杂度较高,性能稳定性较差。
|
图 2 阵列响应方向图 Fig.2 Array response pattern |
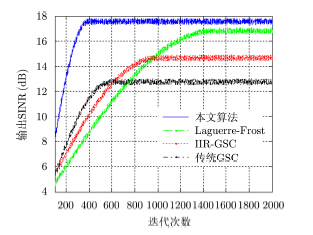
实验2 收敛速度分析
假设迭代次数为100~2000,其他仿真条件不变。比较本文算法、Laguerre-Frost方法、IIR-GSC方法及传统GSC方法在不同迭代次数下输出SINR的变化。
从图 3可以看出,随着迭代次数的增加,所有算法的输出SINR均不断增加。因为本文算法将Laguerre滤波器引入了GSC结构,多极点的计算可以简单地利用最小二乘求解,所以收敛速度较快,在迭代400次左右时输出SINR稳定在17 dB,在整个迭代范围内均高于其他3种算法。Laguerre- Frost方法采用有约束的迭代方式,需迭代1500左右才可以收敛,但输出SINR高于IIR-GSC方法和传统GSC方法。而IIR-GSC方法中基于牛顿迭代方法的多极点和权值的自适应调整过程导致该算法不仅收敛速度较慢,而且在迭代次数小于600次时,输出SINR低于传统GSC方法。
|
图 3 随迭代次数增加时算法输出性能 Fig.3 Output performance versus the number of iterations |
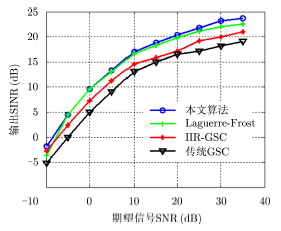
实验3 随SNR增加输出性能分析
假设SNR从-10 dB增加到35 dB,迭代次数为2000,其他仿真参数不变。比较本文算法、Laguerre- Frost方法、IIR-GSC方法及传统GSC方法在不同SNR条件下输出SINR的变化。
从图 4可以看出,随着SNR的增加,所有算法的输出SINR均不断增加,本文算法的输出SINR在整个期望信号SNR范围内均高于其他3种算法。当算法均收敛至最优解时,Laguerre-Frost方法的输出SINR高于IIR-GSC方法和传统GSC方法。但与传统GSC相比,3种宽带波束形成器输出SINR均有提高。因此,在稳定性得到保证的条件下,基于Laguerre滤波器设计的宽带波束形成器的输出性能将优于同阶数的基于FIR滤波器和IIR滤波器设计的自适应波束形成器。
|
图 4 SNR增加时算法输出性能 Fig.4 Output performance versus the SNRs |
本文建立了基于GSC结构的Laguerre宽带波束形成器模型,利用最小二乘方法给出一种低复杂度的极点求解方法,结合NLMS方法实现宽带波束形成。与Laguerre-Frost方法和IIR-GSC方法相比,本文提出的基于GSC结构的Laguerre宽带波束形成器有如下优点:(1)避免了传统IIR滤波器多极点的自适应调整过程,保证了算法的稳定性;(2)简化了Laguerre-Frost方法的极点优化过程;(3)利用GSC结构的无约束自适应求解方法,极大地提高了收敛速度。
| [1] | Liu W and Weiss S. Wideband Beamforming: Concepts and Techniques[M]. Chichester, UK, John Wiley & Sons, 2010: 1-50.( 1) 1) |
| [2] | 范展, 梁国龙. 基于凸优化的最小旁瓣恒定束宽时域宽带波 束形成[J]. 电子学报, 2013, 41(5): 943-949. Fan Zhan and Liang Guo-long. Broadband beamforming with minimum sidelobe and constant beamwidth based on convex optimization[J]. Acta Electronica Sinica, 2013, 41(5): 943-949.(  1) 1) |
| [3] | Zhao Y, Liu W, and Langley R J. An application of the least squares approach to fixed beamformer design with frequency invariant vonstraints[J]. IET Signal Processing, 2011, 5(3): 281-291.( 1) 1) |
| [4] | Frost III O L. An algorithm for linearly constrained adaptive array processing[J]. Proceedings of the IEEE, 1972, 60(8): 926-935.( 1) 1) |
| [5] | Griffiths L J and Jim C W. An alternative approach to linearly constrained adaptive beamforming[J]. IEEE Transactions on Antennas and Propagation, 1982, 30(1): 27-34.( 1) 1) |
| [6] | Vook F W and Compton R T. Bandwidth performance of linear adaptive arrays with tapped delay-line processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(3): 901-908.( 1) 1) |
| [7] | Sekiguchi T and Karasawa Y. Wideband beamspace adaptive array utilizing FIR fan filters for multibeam forming[J]. IEEE Transactions on Signal Processing, 2000, 48(1): 277-284.( 2) 2) |
| [8] | Liu W, Weiss S, and Hanzo L. A subband-selective broadband GSC with cosine-modulated blocking matrix[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(3): 813-820.( 2) 2) |
| [9] | Liu W, Weiss S, and Hanzo L. A generalized sidelobe canceller employing two-dimensional frequency invariant filters[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(7): 2339-2343.( 1) 1) |
| [10] | Gooch R P and Shynk J J. Wideband adaptive array processing using pole-zero digital filters[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 355-367.( 4) 4) |
| [11] | Adkins C N and Turtora J J. A broadband beam former with pole-zero unconstrained jammer rejection in linear arrays[J]. IEEE Transactions on Signal Processing, 1996, 44(2): 438-441.( 2) 2) |
| [12] | Ghavami M and Kohno R. Recursive fan filters for a broadband partially adaptive antenna[J]. IEEE Transactions on Communications, 2000, 48(2): 185-188.( 2) 2) |
| [13] | Duan H, Ng B P, and See C N. A new broadband beamformer using IIR filters[J]. IEEE Signal Processing Letter, 2005, 12(11): 776-779.( 3) 3) |
| [14] | Duan H, Ng B P, See C N, et al.. Broadband beamforming using TDL-form IIR filters[J]. IEEE Transactions on Signal Processing, 2007, 55(3): 990-1003.( 3) 3) |
| [15] | Seydnejad S R and Ebrahimi R. Broadband beamforming using Laguerre filters[J]. Signal Processing, 2012, 92(1): 1093-1100.( 5) 5) |


