空间信号源的参数估计是阵列信号领域的重要研究问题之一。根据信号源与阵列之间的距离远近,可以将其分为远场信号源和近场信号源。当距离r > 2D2/λ (D为阵列孔径,λ为信号源波长),认为信号源为远场,到达阵列的信号以平面波的方式给出,对于信源的定位其距离和波达方向估计是独立的。反之,当0.62(D3/λ)1/2 < r < 2D2/λ时,来波信号通过阵列只能以球面波的形式来表示,信源位置的确定需要联合估计距离和波达方向[1, 2],二者是耦合在一起的。
阵列信号处理中,传统高精度的波达方向(DOA)估计方法都是假设信号源为远场[2],对近场情况则不适用。近年来,许多定位近场源的测向方法被相继提出。文献[3]提出了一种2维MUSIC(MUltiple SIgnal Classification)的定位方法,需要同时搜索估计距离和到达角两个参数,计算量非常大。为了避免多维搜索,文献[4]和文献[5]提出了基于高阶累积量的定位方法,但由于需要构造高阶累量矩阵,运算复杂度同样很高。文献[6]利用2阶累积量,给出了载波频率、距离和角度的3维估计,计算量明显减少,但是在工程应用及硬件实现上仍然有很大的困难。文献[7]利用垂直阵列的特点,将多维参数估计问题转化为1维估计,减小了运算量,但是仅适用于非圆信号。文献[8]利用双基线组合解模糊,也可以用于近场源DOA估计,运算速度快,但是需要距离信息先验已知。文献[9, 10]利用旋转长基线干涉仪在不同转角下测量的相位差序列进行DOA估计,降低了系统复杂性,但是并未考虑近场情况。
基于此,本文提出了一种在工程上易于实现的旋转干涉仪算法来估计近场源的2维角及距离,通过干涉仪基线的旋转实现相位解模糊,只需两个接收通道即可实现快速、无模糊定位[11],并扩展到近场模型。该方法不需要高阶统计量,也不需要1维或2维搜索,从而有效减小了运算复杂度。
本文的各部分内容安排如下:第1节是引言,介绍了近场源参数估计的研究背景及现状。第2节介绍了近场源模型并提出了近场模糊问题。第3节介绍了旋转干涉仪解模糊原理,并提出近场源3维参数估计算法。第4节给出仿真结果和性能分析。最后,第5节得出结论。
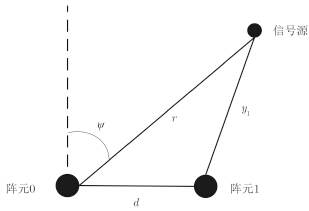
2 问题模型 2.1 近场源信号模型近场源阵列结构示意图如图 1,假设只有1个信号源,阵元间距为d,以阵元0作为相位参考中心,则阵元1接收到的信号可以表示为[3, 12]:
|
图 1 阵列结构示意图 Fig.1 Structure of array |
| ${X_1}(t) = S(t){{\mathop{\rm e}\nolimits} ^{{\mathop{\rm j}\nolimits} {\tau _1}}} + {n_1}(t)$ | (1) |
| $\begin{aligned} {\tau _1} & = 2π f\Delta t = 2π f\frac{{{y_1} - r}}{{\mathop{\rm c}\nolimits} } \hspace{72pt} \\ & = \frac{{2π }}{\lambda }(\sqrt {{r^2} + {d \hspace{1pt} ^2} - 2rd\sin \psi } - r)\\ & = \frac{{2π r}}{\lambda }\Big( \sqrt {1 + \frac{{{d \hspace{1pt} ^2}}}{{{r^2}}} - \frac{{2d\sin \psi }}{r}} - 1 \Big) \end{aligned}$ | (2) |
对式(2)采用2阶泰勒级数展开,如式(3):
| $\sqrt {1 + x} \approx \left( {1 + \frac{x}{2} - \frac{{{x^2}}}{8} + \frac{{{x^3}}}{{16}} + ···} \right),\,\left| x \right| < 1$ | (3) |
| $\begin{aligned} {\tau _1} & = \frac{{2π r}}{\lambda }\Bigg( {1 + \frac{1}{2}\left( {\frac{{{d \hspace{1pt} ^2}}}{{{r^2}}} - \frac{{2d\sin \psi }}{r}} \right) } \\ & \quad - {\frac{1}{8}{{\left( {\frac{{{d \hspace{1pt} ^2}}}{{{r^2}}} - \frac{{2d\sin \psi }}{r}} \right)}^2} + ··· - 1} \Bigg)\\ & \approx - 2π \frac{d}{\lambda }\sin \psi + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\cos ^2}\psi \end{aligned}$ | (4) |
在近场源情况下,由干涉仪两阵元的接收数据进行比相即可获得相位差,即相位差
f = angle (X1(t)/X0(t))
其中X1(t)和X0(t)分别为阵元1和阵元0的接收数据。从式(4)可得两阵元的真实相位差为:| $\begin{array}{l} \phi = - 2π \frac{{d\sin \psi }}{\lambda } + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\cos ^2}\psi = {\phi _1} + {\phi _2} \end{array}$ | (5) |
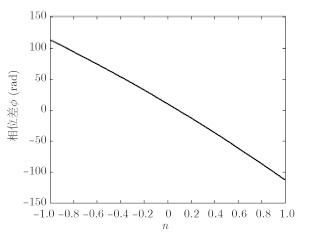
令n=sin$ {\psi} $ ,则相位差可表示为f= $- 2π \frac{d}{\lambda }n + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}(1 - {n^2})$ ,进而可得f与n的关系图,如图 2所示。由图 2可知,n=-1时,相位差取最大值fmax = 2pd/λ; n=1时,相位差取最小值fmin = -2pd/λ。
|
图 2 近场源相位差与n的关系图 Fig.2 Relationship between phase difference and n |
当$\left| \phi \right| \le π $ ,即$ - π \le \phi \le π $ ,则不会出现模糊。由${\phi _{{\rm{min}}}} = - 2π d/\lambda \ge - π $ 和${\phi _{{\rm{max}}}} = 2π d/\lambda \le π $ ,可以得出无模糊的阵元间距为 $d \le \lambda /2$ 。
在工程实现中,天线后端的相位差检测设备(鉴相器)通常以2p为模,只能检测到(-p,p)范围内的相位值。当干涉仪的阵元间距d>λ/2时,相位差f可能大于p。此时,鉴相器只能测得相位差的主值,而非真实相位差。因而会出现相位多值模糊,造成角度测量的多值性。
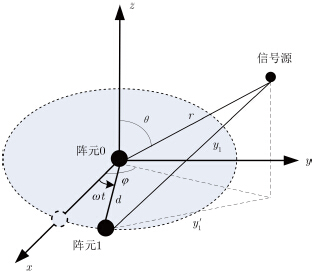
3 用于近场源的旋转干涉仪参数估计算法由2.2节可知,对于单个长基线,存在相位差测量的多值模糊问题。但通过基线的旋转可以解决这些问题[9, 10]。利用旋转长基线干涉仪(Rotated Long Baseline Interferometer,RLBI)在不同转角下测量的相位差序列进行参数估计,与传统多通道干涉仪和阵列测向相比,RLBI系统只需单个长基线,系统复杂性和通道一致性要求大为减低[13]。通过天线绕z轴的旋转(如图 3),鉴相器的相位差积分后按余弦规律变化,进而通过判断极值,实现近场源参数估计。
|
图 3 天线旋转时的阵列模型 Fig.3 Array model of rotating interferometer |
设基线长度为d,其旋转角速度为w。入射信号的俯仰角为$\theta \in [0,π /2)$ ,表示和z轴正方向的夹角;方位角为$\varphi \in [0,2π )$ ,表示从x轴正方向按逆时针方向旋转的角度。信号到达参考阵元的距离为 r,到达阵元1的距离为y1。以图 3为参考,干涉仪绕z轴按逆时针方向旋转,初始时刻位于x轴。则在旋转过程中,两天线间的相位差随之变化。
由余弦定理可得,${y_1}$ 在xoy平面投影${y_1}'$ 为:
| ${y_1}' = \sqrt {{d \hspace{1pt} ^2} + {{(r\sin \theta )}^2} - 2dr\sin \theta \cos (\varphi - \omega t)} $ | (6) |
再由勾股定理可得:
| $\begin{array}{l} {y_1} = \sqrt {{y_1}{{^\prime }^2} + {{(r\cos \theta )}^2}} \\ {\rm{ = }}\sqrt {{d \hspace{1pt} ^2} + {{(r\sin \theta )}^2} - 2rd\sin \theta \cos (\varphi - \omega t) + {{(r\cos \theta )}^2}} \\ {\rm{ = }}\sqrt {{d \hspace{1pt} ^2} + {r^2} - 2rd\sin \theta \cos (\varphi - \omega t)} \end{array} $ | (7) |
所以有:
| $\begin{aligned} {\tau _1} & = \frac{{2π }}{\lambda }\left( {\sqrt {{r^2} + {d \hspace{1pt} ^2} - 2rd\sin \theta \cos (\varphi - \omega t)} - r} \right)\\ & = \frac{{2π r}}{\lambda }\left( {\sqrt {1 + \frac{{{d \hspace{1pt} ^2}}}{{{r^2}}} - \frac{{2d\sin \theta \cos (\varphi - \omega t)}}{r}} - 1} \right) \end{aligned}$ | (8) |
对式(8)采用2阶泰勒级数展开,如式(3),并结合Fresnel近似忽略高阶项,可得到式(9):
| $\begin{aligned} {\tau _1} & = \frac{{2π r}}{\lambda }\Bigg( {1 + \frac{1}{2}\left( {\frac{{{d \hspace{1pt} ^2}}}{{{r^2}}} - \frac{{2d\sin \theta \cos (\varphi - \omega t)}}{r}} \right) } \\ & \quad - {\frac{1}{8}{{\left( {\frac{{{d \hspace{1pt} ^2}}}{{{r^2}}} - \frac{{2d\sin \theta \cos (\varphi - \omega t)}}{r}} \right)}^2} + ··· - 1} \Bigg)\\ & \approx - 2π \frac{{d\sin \theta }}{\lambda }\cos (\varphi - \omega t) \\ & \quad + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}} \left( {1 - {{\sin }^2}\theta {{\cos }^2}(\varphi - \omega t)} \right)\\ & = {\phi _1}\cos (\varphi - \omega t) + {\phi _2} + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta {\sin ^2}(\varphi - \omega t) \end{aligned}$ | (9) |
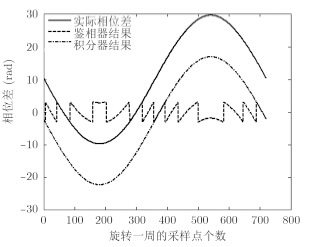
当q一定时,天线的旋转可以使相位差f(t)按照近似余弦规律变化,如图 4中实线所示。但是通过数字鉴相器后相位差被限定在(-p,p)范围内,故鉴相器得到的相位差变化曲线存在跳变现象,如图 4中虚线所示。所以,鉴相器的输出并非完整的相位差,从而不能直接根据鉴相器的输出得到f1和f2,需采用数字积分器[9]对鉴相器的输出进行积分。
|
图 4 旋转一周过程中的相位差变化曲线 Fig.4 Phase difference curve in one rotation |
图 4中点划线是数字积分器的输出,记为X(t)。由图 4可知,通过积分成功消除了相位跳变现象,恢复出完整的相位差变化曲线。然而由于积分器的起始值(初始时刻值)为鉴相器的输出,所以积分结果X(t)虽然形状与实际曲线f(t)相同,但是相对于实际曲线存在一个整体的偏移量D。
图 4中横坐标表示天线以角速度w旋转一周过程中的空间采样点,即空间快拍。纵坐标为不同空间采样点处对应的相位差。
3.2 近场源参数估计由式(9)可知,在基线旋转过程中,当cos(j-wt)=1时,瞬时相位为:
| $\phi (t) = - 2π \frac{{d\sin \theta }}{\lambda } + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\cos ^2}\theta = {\phi _1} + {\phi _2} = {\phi _{{\rm{min}}}}$ | (10) |
当cos(j-wt)=-1时,瞬时相位为:
| $\phi (t) = 2π \frac{{d\sin \theta }}{\lambda } + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\cos ^2}\theta = - {\phi _1} + {\phi _2} = {\phi _{{\rm{max}}}}$ | (11) |
由实际相位差曲线的极大值fmax和极小值fmin就可以确定f1和f2的值。它们之间满足式(12)关系式:
| $\left. \begin{array}{l} {\phi _{{\rm{max}}}} = - {\phi _1} + {\phi _2}\\ {\phi _{{\rm{min}}}} = {\phi _1} + {\phi _2} \end{array} \right\}$ | (12a) |
| $\left. \begin{array}{l} \quad \quad \quad {\phi _1} = - \frac{1}{2}({\phi _{{\rm{max}}}} - {\phi _{{\rm{min}}}})\\ \quad \quad \quad {\phi _2} = \frac{1}{2}({\phi _{{\rm{max}}}} + {\phi _{{\rm{min}}}}) \end{array} \right\}$ | (12b) |
确定了f1和f2后,就可以根据式(13)求出q和r。
| $\left. \begin{array}{l} {\phi _1} = \frac{{ - 2πd\sin \theta }}{\lambda }\\ {\phi _2} = \frac{{π {d \hspace{1pt} ^2}{{\cos }^2}\theta }}{{\lambda r}} \end{array} \right\}$ | (13) |
由式(13)可得:
| $\sin \theta = \frac{{{\phi _1}\lambda }}{{ - 2π d}}$ | (14a) |
| $r = {{\pi {d^2}{{\cos }^2}\theta } \over {{\phi _2}\lambda }}\\ \;\, = {{\pi {d^2}} \over {{\phi _2}\lambda }}\left( {1 - {{\phi _1^2{\lambda ^2}} \over {4{\pi ^2}{d^2}}}} \right)$ | (14b) |
进而得到q和r估计的闭式解:
| $\left. \begin{array}{l} \theta = {\rm{arc}}{\rm{sin}}\Big(\frac{{{\phi _1}\lambda }}{{ - 2π d}}\Big)\\ r = \frac{{π {d \hspace{1pt} ^2}}}{{{\phi _2}\lambda }}\left( {1 - \frac{{\phi _1^2{\lambda ^2}}}{{4{π ^2}{d \hspace{1pt} ^2}}}} \right) \end{array} \right\}$ | (15) |
在完成以上估计的基础上,求解下式所示方程可以得到方位角j的估计:
| $\phi (0) = {\phi _1}\cos \varphi + {\phi _2} + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta (1 - {\cos ^2}\varphi )$ | (16) |
由于鉴相器的初始时刻相位差j0可能存在模糊,所以积分结果X(t)与实际曲线f(t)之间存在一个整体的偏移量D=2pn,其中n为整数,表示初始时刻鉴相结果的模糊倍数。即:
| $X(t) + \Delta = \phi (t)$ | (17) |
由于f1=-(1/2)(fmax-fmin),仅仅和实际相位差极大值与极小值的差值有关,所以由积分结果的极大值与极小值的差值即可以得到f1的估计
| ${\phi _1} = - \frac{1}{2}({X_{{\rm{max}}}} - {X_{{\rm{min}}}})$ | (18) |
然而由于f2=(1/2)(fmax+fmin),应该由实际相位差曲线的极大值和极小值计算。此时就需要对积分结果X(t)进行修正,以得到实际的相位差曲线。
在式(17)中D为常量,所以X(t)和f(t)的导数是相等的,即有:
| $X''(t) = \phi ''(t)$ | (19) |
对f(t)求2阶导数,得
| $\begin{aligned} \phi ''(t) & = - {\phi _1}{\omega ^2}\cos (\varphi - \omega t) \\ & \quad \,+ 2{\omega ^2}π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta \cos [2(\varphi - \omega t)] \\ & = \frac{{2π d\sin \theta }}{\lambda }{\omega ^2}\cos (\varphi - \omega t) \\ & \quad \,+ 2{\omega ^2}π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta \cdot [2{\cos ^2}(\varphi - \omega t) - 1] \end{aligned}$ | (20) |
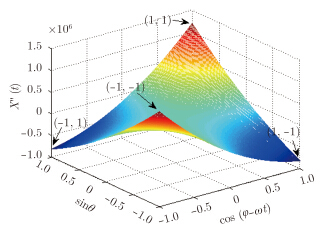
以cos(j-wt)为X轴,sinq为Y轴,作出相位差2阶导数的图如图 5所示。
|
图 5 相位差变化曲线的2阶导数 Fig.5 Second derivative of phase difference curve |
由图 5可知,该曲面关于Y=-X+1(即sinq=-cos(j-wt)+1)这条线对称。一般情况下,对于sinq > 0,最大值分布右半平面,即cos(j-wt)=1时,相位差2阶导数取最大值f"(t)max = ((2pdsinq / λ)
· ω2) + (2ω2p · (d2 / (λr)) · sin2q);对于sinq < 0,
cos(j-wt)=-1时,相位差2阶导数取最大值$\phi ''{(t)_{{\rm{max}}}} = - \frac{{2π d\sin \theta }}{\lambda }{\omega ^2} + 2{\omega ^2}π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta $ 。
由式(20)中$\phi ''(t)$ 的表达式也可看出,一般情况下,对于给定的sinq > 0,cos(j-wt)=1时,$\phi ''(t)$ 的第1项和第2项均为最大,故相位差2阶导数取最大值$\phi ''{(t)_{{\rm{max}}}} = \frac{{2π d\sin \theta }}{\lambda }{\omega ^2} + 2{\omega ^2}π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta $ ;对于给定的sinq < 0,cos(j-wt)=-1时,$\phi ''(t)$ 的第1项和第2项均为最大,故相位差2阶导数取最大值$\phi ''{(t)_{{\rm{max}}}} = - \frac{{2π d\sin \theta }}{\lambda }{\omega ^2} + 2{\omega ^2}π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta $ 。
综上所述:
| $\phi ''{(t)_{{\rm{max}}}} = \frac{{2π d\left| {\sin \theta } \right|}}{\lambda }{\omega ^2} + 2{\omega ^2}π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta $ | (21) |
特别地,当cos(j-wt)=1,sinq=1或者cos(j-wt)=-1,sinq=-1时,相位差2阶导数取全局最大值$\phi ''{(t)_{{\rm{gmax}}}} = \frac{{2π d}}{\lambda }{\omega ^2} + \frac{{2π {\omega ^2}{d \hspace{1pt} ^2}}}{{\lambda r}}$ ;当cos(j-wt)=-1,sinq=1或者cos(j-wt)=1,sinq=-1时,相位差2阶导数取全局最小值$\phi ''{(t)_{{\rm{gmin}}}} = - \frac{{2π d}}{\lambda }{\omega ^2} + \frac{{2π {\omega ^2}{d \hspace{1pt} ^2}}}{{\lambda r}}$ 。
由式(19)可得:
| $\begin{aligned} X''{(t)_{{\rm{max}}}} & = \phi ''{(t)_{{\rm{max}}}} \\ & = \frac{{2π d\left| {\sin \theta } \right|}}{\lambda }{\omega ^2} + 2{\omega ^2}π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta \end{aligned}$ | (22) |
则目标距离r如式(23)所示:
| $r = \frac{{2π {\omega ^2}{d \hspace{1pt} ^2}{{\sin }^2}\theta }}{{\lambda X''{{(t)}_{{\rm{max}}}} - 2π d\left| {\sin \theta } \right|{\omega ^2}}}$ | (23) |
因为q和r已经由前面估计得到,故可以获得f2的估计,即实际曲线值的中点(中点的含义为最大值和最小值的均值):
| ${\phi _2} = \frac{1}{2}({\phi _{{\rm{max}}}} + {\phi _{{\rm{min}}}}) = \frac{{π {d \hspace{1pt} ^2}{{\cos }^2}\theta }}{{\lambda r}}$ | (24) |
积分结果的中点为:
| ${\phi _2}_{{\rm{mod}}} = \frac{1}{2}({X_{{\rm{max}}}} + {X_{{\rm{min}}}})$ | (25) |
所以整体的修正量D可由实际曲线值的中点f2和积分结果值的中点f2mod的差值来度量。即:
| $\Delta = \phi (t) - X(t) = {\phi _2} - {\phi _{{\rm{2mod}}}}$ | (26) |
则修正后的积分结果为:
| ${X_{{\rm{up}}}}(t) = X(t) + \Delta = \hat \phi (t)$ | (27) |
Xup(t)为相位差变化曲线f(t)的估计。进而由f(t)的初值以及f1和f2来估计方位角j:
| $\phi (0) = {\phi _1}\cos \varphi + {\phi _2} + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta {\sin ^2}\varphi $ | (28) |
式(28)中仅方位角j未知,因此通过求解式(29)所示的2次方程:
| $\phi (0) = {\phi _1}\cos \varphi + {\phi _2} + π \frac{{{d \hspace{1pt} ^2}}}{{\lambda r}}{\sin ^2}\theta (1 - {\cos ^2}\varphi )$ | (29) |
综上所述,基于旋转干涉仪的近场源参数估计算法步骤总结如下:
步骤1 通过干涉仪的旋转获得不同转角下的有模糊的相位差序列(即鉴相器输出);
步骤2 利用数字积分方法恢复出完整的相位差序列X(t);
步骤3 由积分结果的极大值和极小值之差可以确定f1的值,如式(18)所示,进而由式(15)可得俯仰角q的估计;
步骤4 对积分结果X(t)求2阶导数,即可由式(23)求得r;
步骤5 利用获得的q和r,根据式(24)得到f2,即实际相位差曲线的中点,并由式(25)获得积分结果的中点f2mod;
步骤6 由式(26)获得实际曲线和积分结果的偏移量D,进而由式(27)得到修正后积分结果,即实际相位差曲线的估计;
步骤7 由实际相位差曲线的初值,求解式(29)所示的方程,即得方位角j,完成近场源的俯仰角、方位角和距离估计。
4 仿真实验和性能分析本节通过仿真实验对旋转干涉仪的近场参数估计性能进行分析,并将其参数估计性能与双长基线干涉仪方法和基于均匀圆阵方法[14]进行比较。其中,双长基线干涉仪的阵列模型如图 6所示。

|
图 6 双长基线干涉仪阵列模型 Fig.6 Array model of DLBI |
根据3.3节本文算法步骤可知,本文算法对俯仰角、方位角以及距离参数的估计精度依赖于相位差序列X(t)的估计精度。在不同的SNR条件下,X(t)的估计精度不同,由于误差传递效应,导致后续的俯仰角、方位角以及距离参数估计精度也会不同。下面通过仿真实验给出相位差误差随0.35pt;">输入信噪比的变化关系。
仿真实验1 入射信号频率为3 GHz,中心波长λ=0.1 m,入射俯仰角q为10°,方位角j为40°,距离r为10 m。旋转干涉仪由2个阵元组成,基线的长度d = 18λ,干涉仪旋转频率fr = 15 Hz,旋转一周的采样点数为720个。快拍数为200,蒙特卡洛实验次数为100。
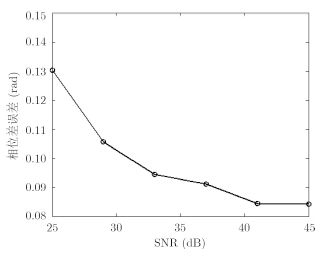
由图 7可知,随着SNR增大,相位差误差逐渐减小。当SNR高于30 dB时,相位差误差保持在较小的恒定水平,从而有利于提高后续的俯仰角、方位角以及距离参数估计精度。
|
图 7 相位差误差随SNR变化关系图 Fig.7 Relationship of phase error versus SNR |
下面通过仿真实验给出本文算法对俯仰角、方位角以及距离参数的估计精度。
参数设置:入射信号频率为3 GHz,中心波长λ=0.1 m,入射俯仰角q为10°,方位角j为40°。旋转长基线干涉仪由2个阵元组成,基线的长度d = 18λ,基线旋转频率fr = 15 Hz,旋转一周的采样点数为720个。双长基线干涉仪由3个阵元组成,两基线长度分别为d1 = 8λ,d2 = 10λ。两种干涉仪具有相同的菲涅尔区[4.7 m,64.8 m],入射近场源与阵列之间的距离设定为10 m。
仿真实验2 200次Monte-Carlo实验,SNR取值区间为[25, 45] dB,间隔为2 dB。分析俯仰测向、方位测向以及测距均方根误差(Root Mean Square Error,RMSE)随信噪比的变化关系。
由图 8可知,随着信噪比增大,俯仰、方位测向和测距的均方根误差逐渐减小。由图 8(a)可知,当SNR<30 dB时,双长基线干涉仪法性能较差。当在上述SNR设定范围内,旋转干涉仪的俯仰测向RMSE小于双长基线干涉仪方法和基于均匀圆阵的方法。由图 8(b)可知,旋转干涉仪的方位测向RMSE在0.02°以下,小于基于均匀圆阵的方法。由图 8(c)可知,旋转干涉仪的测距RMSE在0.1 m以下,大于基于均匀圆阵的方法。

|
图 8 俯仰、方位测向以及测距均方根误差随信噪比变化关系图 Fig.8 Elevation,azimuth and distance measurements RMSE versus SNR |
值得注意的是,双长基线干涉仪方法需要距离已知,且只能对1维角度进行估计;而基于均匀圆阵的方法没有考虑模糊问题;而本文方法不需要距离信息先验已知,能对近场源的3维参数进行估计,且能实现解模糊,所以具有一定优势。
仿真实验3 100次Monte-Carlo实验,SNR=35 dB,快拍数取值范围为[200, 1000],间隔为100。分析俯仰测向、方位测向以及测距均方根误差随快拍数变化关系。
由图 9可知,随着快拍数增加,俯仰、方位测向和测距的均方根误差逐渐减小。由图 9(a)可知,当快拍数大于200时,旋转干涉仪方法对应的俯仰测向RMSE小于0.001°,且小于双长基线干涉仪方法和基于均匀圆阵的方法对应的俯仰测向误差。由图 9(b)可知,旋转干涉仪的方位测向RMSE在0.01°左右,小于基于均匀圆阵的方法。由图 9(c)可知,旋转干涉仪的测距RMSE在0.1 m以下,大于基于均匀圆阵的方法。

|
图 9 俯仰、方位测向以及测距均方根误差随快拍数变化 Fig.9 Elevation,azimuth and distance measurements RMSE versus snapshots |
设定测向误差在$ \pm $ 1°内视为正确解模糊,通过统计在给定的Monte-Carlo实验次数(Mt)中正确解模糊次数(CUA),即可得正确解模糊概率。定义正确模糊概率P为:
| $P = \frac{{{\rm{CUA}}}}{{{\rm{Mt}}}} \times {\rm{100}}\% $ | (30) |
仿真实验4 100次Monte-Carlo实验,SNR取值范围为[0, 30] dB,间隔为3 dB。分析正确解模糊概率随信噪比变化。
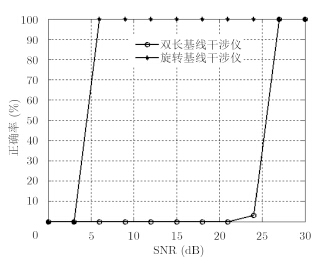
性能分析:由图 10可知,当 ${\rm{SNR}} \ge 6 \,{\rm{dB}}$ 时,旋转干涉仪方法即可达到100%的正确解模糊概率;而双长基线干涉仪方法当 ${\rm{SNR}} \ge 27 \,{\rm{dB}}$ 时才能达到100%的正确解模糊概率。可以看出,在低信噪比条件下,相比于双长基线干涉仪方法,旋转干涉仪方法具有显著的解模糊优势。
|
图 10 正确解模糊概率随信噪比变化 Fig.10 Correctly solving ambiguity probability versus SNR |
本文针对单个长基线干涉仪的阵列结构,提出一种对近场源信号进行3维参数估计的旋转干涉仪算法,可以给出俯仰角、方位角和距离估计的闭式解。仿真结果表明,所提算法在参数估计精度以及解模糊能力上均优于双长基线干涉仪方法和基于均匀圆阵方法,而且具有更简单的系统结构,因而利于工程应用。该算法只能处理单个近场信号源,无法解决存在多个信号源情况下的参数估计问题,推广到多个信号源是需要进一步探讨的问题。此外,本文所提近场源参数估计方法主要采用个别特征点处的相位差进行估计,而没有利用其它点的信息,因此在低SNR条件下的稳定性可能较差。如何充分利用相位差的全部信息以提高低SNR下的参数估计精度以及稳定性是我们下一步研究的方向。
| [1] | Jiang Jia-jia, Duan Fa-jie, Chen Jin, et al.. Mixed near-field and far-field sources localization using the uniform linear sensor array[J]. IEEE Sensors Journal, 2013, 13(8): 3136-3143.( 1) 1) |
| [2] | Kim J H, Yang I S, Kim K M, et al.. Passive ranging sonar based on multi-beam towed array[C]. OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, 2000, 3: 1495-1499.
( 1) 1) |
| [3] | Huang Y D and Barkat M. Near-field multiple sources localization by passive sensor array[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(7): 968-975.
( 2) 2) |
| [4] | 陈建峰, 张贤达, 吴云韬. 近场源距离、频率及到达角联合估 计算法[J]. 电子学报, 2004, 32(5): 803-806. Chen Jian-feng, Zhang Xian-da, and Wu Yun-tao. An algorithm for jointly estimating range, DOA and frequency of near field source[J]. Acta Electronica Sinica, 2004, 32(5): 803-806. (  1) 1) |
| [5] | 黄家才, 石要武, 陶建武. 一种新的近场源距离及到达角联合 估计算法[J]. 电子与信息学报, 2007, 29(11): 2738-2742. Huang Jia-cai, Shi Yao-wu, and Tao Jian-wu. A new method for range and DOA estimation of near-field sources[J]. Journal of Electronics & Information Technology, 2007, 29(11): 2738-2742. (  1) 1) |
| [6] | 王波, 王树勋. 一种基于二阶统计量的近场源三维参数估计方 法[J]. 电子与信息学报, 2006, 28(1): 45-49. Wang Bo and Wang Shu-xun. A three-dimensional parameter estimation method of near field sources based on second statistics[J]. Journal of Electronics & Information Technology, 2006, 28(1): 45-49. (  1) 1) |
| [7] | 王凌, 李国林, 谢鑫, 等. 非圆信号二维DOA和初始相位联合 估计方法[J]. 雷达学报, 2012, 1(1): 43-49. Wang Ling, Li Guo-lin, Xie Xin, et al.. Joint 2-D DOA and noncircularity phase estimation method[J]. Journal of Radars, 2012, 1(1): 43-49. (  1) 1) |
| [8] | 曹菲, 刘庆云. 双基线干涉仪解模糊能力分析[J]. 航天电子对 抗, 2013, 29(3): 24-25. Cao Fei and Liu Qing-yun. Analysis on ability of dualbaseline interferometer to resolve angular ambiguities[J]. Aerospace Electronic Warfare, 2013, 29(3): 24-25. (  1) 1) |
| [9] | 司伟建, 程伟. 旋转干涉仪解模糊方法研究及实现[J]. 弹箭与 制导学报, 2010, 30(3): 199-202. Si Wei-jian and Cheng Wei. Study on solving ambiguity method of rolling interferometer and implemention[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(3): 199-202.(  3) 3) |
| [10] | 刘鲁涛, 司锡才. 开环旋转相位干涉仪DOA算法分析[J]. 解放 军理工大学学报, 2011, 12(5): 419-424. Liu Lu-tao and Si Xi-cai. Analysis of DOA algorithim by open loop method of rotating phase interferometer system[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2011, 12(5): 419-424. (  2) 2) |
| [11] | 李腾, 郭福成, 姜文利. 基于旋转干涉仪模糊相位差的多假设 NLS定位算法[J]. 电子与信息学报, 2012, 34(4): 956-961. Li Teng, Guo Fu-cheng, and Jiang Wen-li. Multiple hypothesis NLS location algorithm based on ambiguous phase difference measured by a rotating interferometer[J]. Journal of Electronics & Information Technology, 2012, 34(4): 956-961.(  1) 1) |
| [12] | Krim H and Viberg M. Two decades of array processing research: the parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94.( 1) 1) |
| [13] | 张敏, 郭福成, 李腾, 等. 旋转长基线干涉仪测向方法及性能分 析[J]. 电子学报, 2013, 41(12): 2422-2429.. Zhang Min, Guo Fu-cheng, Li Teng, et al.. A direction finding method and analysis based on the rotated long baseline interferometer[J]. Acta Electronica Sinica, 2013, 41(12): 2422-2429.(  1) 1) |
| [14] | Wu Yun-tao, Wang Hai, Huang Long-ting, et al.. Fast algorithm for three-dimensional single near-field source localization with uniform circular array[C]. IEEE CIE International Conference, Chengdu, 2011: 350-352.( 1) 1) |


