②University of Chinese Academy of Sciences, Beijing 100190, China
合成孔径雷达(SAR)从后向散射测量中定量反演地球物理参数[1, 2],根据具体的应用,必须进行相应程度的辐射定标,它通过在成像场景内布设已知雷达截面积(RCS)的人造参考点目标来实现[3]。
对于窄带和窄方位波束SAR系统,可以认为定标参考点目标的RCS在工作带宽和方位波束内近似恒定[4, 5, 6]。然而,随着遥感应用中对图像分辨率要求的提高,产生了很多高分辨率SAR系统,相对带宽可以超过10%甚至达到100%,且方位入射角范围可以从几度增加到几十度甚至360°(圆迹SAR)。在现代高分辨率SAR系统大距离向带宽和宽方位向波束的特点下,用中心频率和方位角处的RCS近似表示参考目标的后向散射特性,已不能达到辐射定标的精度要求。文献[7]中针对低频UWB-SAR定标技术,建立了适用于UWB-SAR的辐射定标模型,但其工作在VHF/UHF波段,距离分辨率较低,严格意义上不属于高分辨率SAR;文献[8]中对高分辨率SAR参考点目标辐射特性和校正方法进行了研究,提出了高分辨率条件下角反射器的研制要求,但采用高频近似公式法,分析结果存在较大误差。文献[9, 10]揭示了传统RCS定义所导致的SAR图像辐射观测不准确性现象,并提出了等效RCS的概念,但没有给出定量分析结果或解决方案。
本文在建立高分辨率SAR辐射定标模型的基础上,借助FEKO 3维电磁仿真软件,获取参考目标RCS随频带和方位入射角的变化关系,结合高分辨率SAR系统仿真,定量地分析参考目标RCS的频带或方位角相关性对SAR图像质量的影响。
2 高分辨率SAR辐射定标的数学模型通过雷达方程建立目标散射特性与回波信号的量化关系是辐射定标理论分析的前提,考虑到高分辨率SAR系统具有大的距离向带宽和宽方位向波束,雷达方程中的参量随频率和方位角的变化不能忽略,本文以点目标雷达方程为例进行分析,但不失一般性,因为在辐射定标过程中分布式目标后向散射系数的确定依赖于那些已知散射特性的点目标的先验测量,则SAR图像的平均接收信号功率可以表示为:
| ${{P}_{\text{r}}}=\frac{{{P}_{\text{t}}}{{G}^{2}}(f,\alpha ){{G}_{\text{s}}}(f){{\lambda }^{3}}(f){{\tau }_{\text{p}}}{{f}_{\text{s}}}{{f}_{\text{PRF}}}}{2{{(4\pi )}^{3}}{{R}^{3}}(\alpha )V{{\rho }_{\text{a}}}}\sigma (f,\alpha )+{{P}_{\text{n}}}$ | (1) |
SAR系统的发射信号通常采用线性调频或者步进频脉冲形式,在大带宽下的起始和终止频率段,目标RCS很难保持恒定,且如果SAR系统具有很高的方位向分辨率,目标RCS在相干处理的方位角范围内变化也会比较剧烈,因此,目标散射特性σ(f,α)近似恒定的假设不再成立,而应该表示为:
| $\sigma (f,\alpha ) = A(f,\alpha ){{\rm{e}}^{\rm{j}\mathit{\psi (f,\alpha )}}}$ | (2) |
SAR接收机记录的目标数据位复幅度S(x,y),x和y是空间坐标,忽略噪声影响,那么SAR复图像可以表示为:
| $V \,(x,y) = \sqrt K S(x,y) * h(x,y)$ | (3) |
| $S(x,y) = \sqrt \sigma \delta (x,y)$ | (4) |
而考虑参考目标RCS的频带和方位角相关性后,式(4)变为:
| ${S^\prime }(x,y) = \sqrt {{\sigma ^\prime }} {\delta' \! _{{\rm{PSF}}}}(x,y)$ | (5) |
| $P(x,y) = {\left| {V \,(x,y)} \right|^2} = K{\sigma ^\prime }{\left| {{{\delta'} \! _{{\rm{PSF}}}}(x,y) * h(x,y)} \right|^2}$ | (6) |
进而,点目标积分像素强度可以表示为:
| $I=\iint_{\Omega }{{}}P(x,y)\text{d}x\text{d}y \\ \ \ =K{{\sigma }^{\prime }}\iint_{\Omega }{{}}{{\left| {\delta }'{{}_{\text{PSF}}}(x,y)*h(x,y) \right|}^{2}}\text{d}x\text{d}y$ | (7) |
参考目标RCS是定义在远场即平面波照射条件下,用来度量雷达目标对入射电磁波散射能力的一个物理量。另外,表征由波长归一化的目标特征尺寸大小的参数称为kl值[11],即kl=2πι/λ。按目标电磁后向散射特性的不同将kl分为3个区域:瑞利区,工作波长大于目标特征尺寸,一般取kl<0.5的范围;谐振区,一般在0.5≤kl≤20的范围;光学区(又称高频区),一般取kl>20。高分辨率SAR系统通常工作在X,Ku或Ka波段,对于常规尺寸的常用参考目标,均工作在光学区。
SAR辐射定标通常采用角反射器、有源定标器等参考目标来获取系统传递函数及定标常数,点目标的不确定性将直接影响SAR辐射定标的精度。对于有源定标器,可以通过自动控制获得在整个频带和波束宽度内恒定的RCS响应,但需要精确地功率补偿操作,其面临的根本问题同无源定标器是一样的,因此,本文以无源定标器为例进行分析。对于无源参考目标,如圆柱体、球体等,角反射器在同样的特征尺寸下具有更大的RCS和3 dB带宽,且稳定性较好,因此,本文以三面体角反射器[12, 13]为例进行分析。文献[14]给出由几何光学法计算得到的三面体角反射器RCS近似表达式:
| $\delta (\theta ,\varphi )\approx \frac{4\pi }{{{\lambda }^{2}}}{{l}^{4}}{{\left\{ \cos \theta +\sin \theta \left( \sin \varphi +\cos \varphi \right)-2{{\left[ \cos \theta +\sin \theta \left( \sin \varphi +\cos \varphi \right) \right]}^{-1}} \right\}}^{2}}$ | (8) |
当θ=54.74°,ψ=45°时,即取得最大RCS值4πι4/3λ2,但是考虑到上述理论公式是经过几何光学法近似获得,只对三面体角反射器口面的法线方向附近是有效的,对其它频点和方位角获得的RCS误差较大。因此,本文采用FEKO软件中的多层快速多极子方法(MLFMM)来获取三面体角反射器RCS随频带和方位角的变化关系,MLFMM是研究电大尺寸目标问题的快速高效数值算法,它使得在小型计算机上解决大规模的电磁散射问题成为可能。
首先,根据高分辨率SAR大距离带宽和宽方位波束的特点,在如下条件下,构建参考目标的电磁散射仿真几何模型:在Ku波段远场照射条件下,工作中心频率为f0=16 GHz,带宽△f分别为0.5 GHz,1.0 GHz,2.0 GHz,4.0 GHz;俯仰角为固定值θ=54.74°,方位角以ψ=45°为中心,方位角变化△ψ分别为5°,10°,20°,30°;三面体角反射器尺寸为ι=20 cm,满足ι≈10λ,即目标散射特性属于高频区;其次,用MATLAB读取由FEKO导出的ffe文件,提取RCS数据,合成2维矩阵,第1维度代表波束宽度内的方位角变化,第2维度代表距离带宽内的频率变化;最后,需要综合考虑PC机的配置和FEKO工程的计算量,本文取频率步长为20 MHz,方位角步长为0.2°,在离散点数已能够反映出曲线变化趋势的情况下,可以采用插值处理来降低运算量,从而避免工程规模过大,运算时间过长。
3.1 带宽对参考目标RCS的影响首先,在较小的方位波束情况下,观察参考目标RCS随距离带宽的变化情况,4组参数设定如下,第1组参数:△f=0.5 GHz,△ψ=5°;第2组参数:△f=1.0 GHz,△ψ=5°;第3组参数:△f=2.0 GHz,△ψ=5°;第4组参数:△f=4.0 GHz,△ψ=5°。分别绘制归一化RCS曲面及对应的中心剖面曲线,并记录在每组参数情况下RCS随频带的最大变化量,结果如图 1,图 2所示。
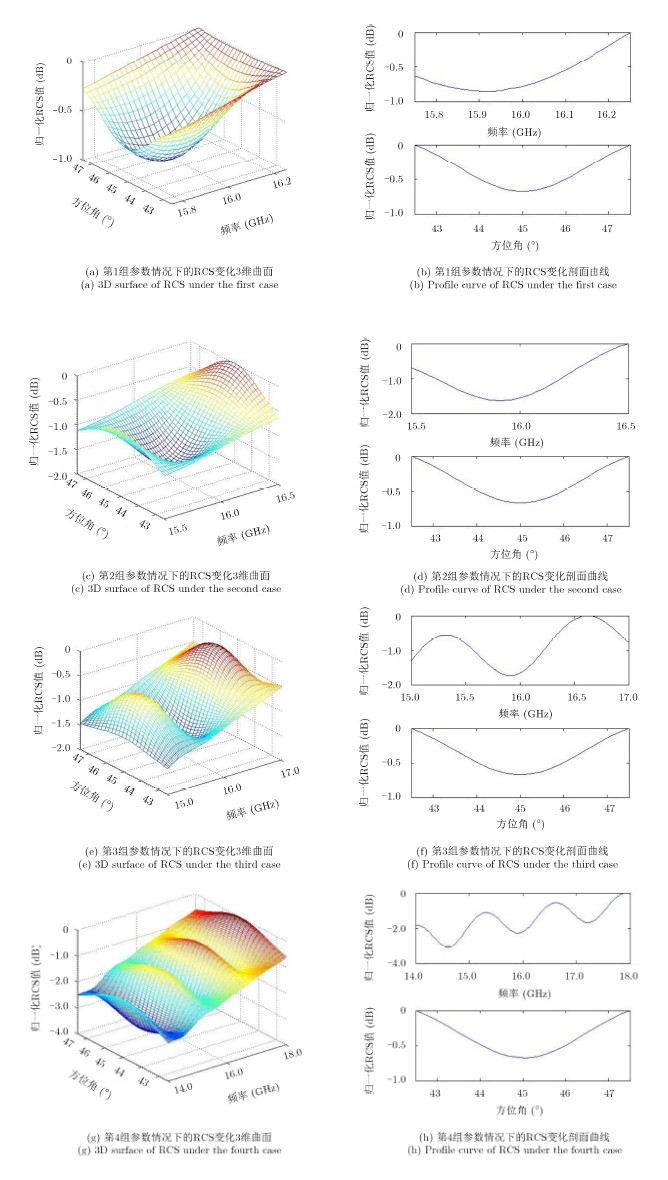
|
图 1 RCS随带宽的变化关系 Fig.1 Variation of RCS with different bandwidths |
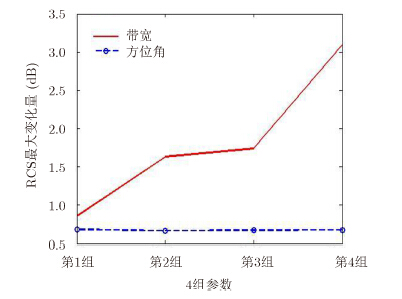
|
图 2 RCS随频带的最大变化量 Fig.2 Maximum variation of RCS with different bandwidths |
通过图 1,图 2可知,由于方位角变化△ψ固定为5°,RCS随方位角的最大变化量基本相同;而随着SAR系统带宽变大,参考目标RCS随频带的最大变化量增大,在带宽超过2.0 GHz时,RCS的最大变化量呈显著上升趋势,在△f=4.0 GHz时甚至超过3 dB。
3.2 方位波束对参考目标RCS的影响接下来,在较小的带宽情况下,观察参考目标RCS随不同宽度方位波束的变化情况,4组参数设定如下,第5组参数:△ψ=5°,△f=0.5 GHz,同上节第1组参数;第6组参数:△ψ=10°,△f=0.5 GHz;第7组参数:△ψ=20°,△f=0.5 GHz;第8组参数:△ψ=30°,△f=0.5 GHz。分别绘制归一化RCS曲面及对应的中心剖面曲线,并记录在每组参数情况下RCS随方位角的最大变化量,结果如图 3,图 4所示。
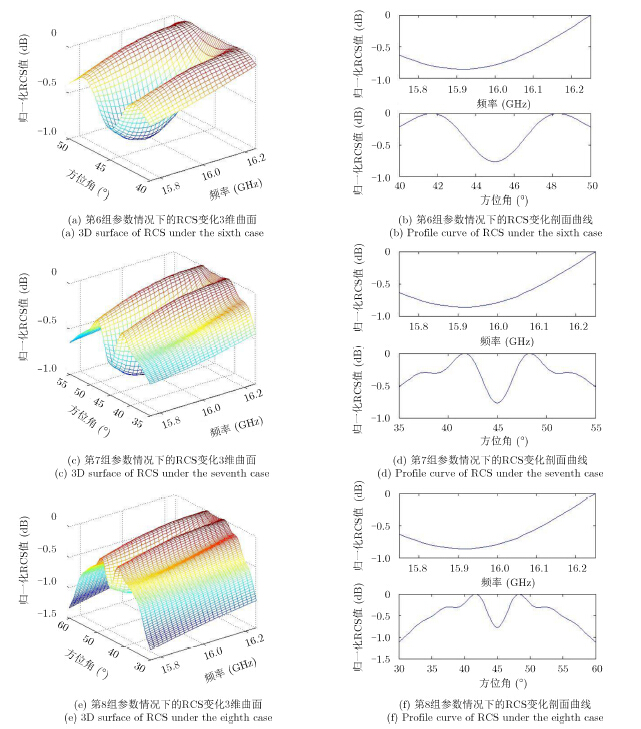
|
图 3 RCS随方位波束的变化关系 Fig.3 Variation of RCS with different azimuth beamwidths |
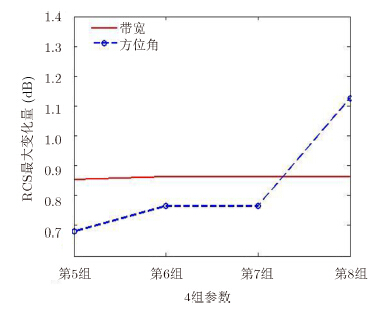
|
图 4 RCS随方位角的最大变化量 Fig.4 Maximum variation of RCS with different azimuth beamwidths |
通过图 3,图 4可知,由于带宽△f固定为0.5 GHz,RCS随频带的最大变化量基本相同;而随着方位波束变宽,参考目标RCS随方位角的最大变化量增大,在波束宽度超过5°时,RCS的最大变化量呈显著上升趋势,在△ψ=30°时已超过1 dB。
3.3 二者共同作用对参考目标RCS的影响最后,针对高分辨率SAR大距离带宽和宽方位波束的特点,观察参考目标RCS随不同带宽和方位波束的变化情况,4组参数设定如下,第9组参数:△f=0.5 GHz,△ψ=5°,同前两节第1,第5组参数;第10组参数:△f=0.5 GHz,△ψ=10°;第11组参数:△f=0.5 GHz,△ψ=20°;第12组参数:△f=0.5 GHz,△ψ=30°。分别绘制归一化RCS曲面及对应的中心剖面曲线,并记录在每组参数情况下RCS随频带和方位角的最大变化量,结果如图 5,图 6所示。
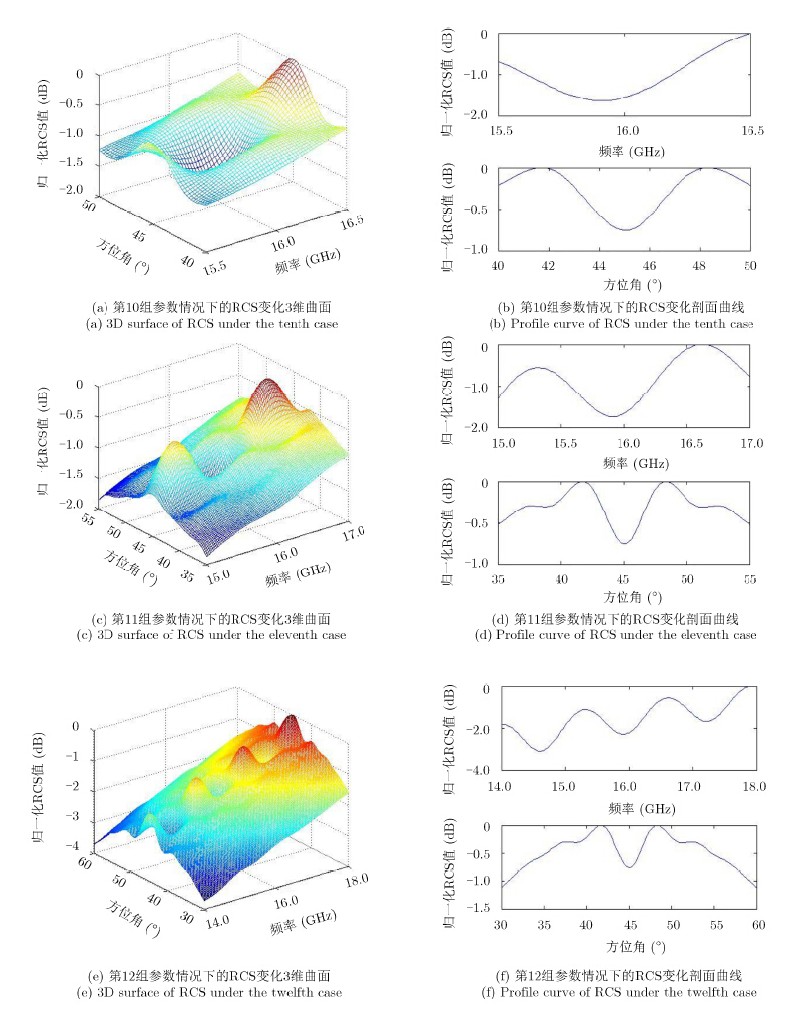
|
图 5 RCS随带宽和方位波束的变化关系 Fig.5 Variation of RCS with different bandwidths and beamwidths |
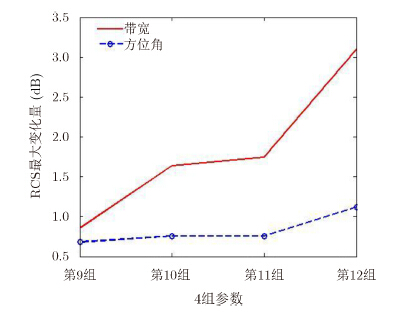
|
图 6 RCS随频带和方位角的最大变化量 Fig.6 Maximum variation of RCS with different bandwidths and beamwidths |
通过图 5,图 6可知,随着带宽变大和方位波束变宽,参考目标RCS的变化也越大;在带宽超过2.0 GHz或波束宽度超过5°时,RCS的变化均呈显著上升趋势,在△f=4.0 GHz,△ψ=10°时,二者的共同影响已超过4 dB;另外,通过对比各图可以发现,带宽和方位波束对RCS的共同作用基本相当于单个分量影响的叠加。
综上,在高分辨率SAR系统大距离带宽和宽方位波束条件下,可以看到RCS随频带和方位角的变化比较剧烈,不能像常规SAR辐射定标一样,利用中心频点散射值代替带宽内各频点的散射值,及利用中心方位角散射值代替整个波束宽度内各个方位角的散射值,必须考虑参考目标RCS随频带和方位角的变化。
4 点目标成像仿真分析通常,在整个SAR系统辐射误差分配中,参考目标散射特性变化引起的误差,有源设备不能超过0.2 dB,无源设备不能超过0.3 dB。为了更加直观地分析上述RCS变化对最终SAR图像的影响,本文对机载聚束模式SAR工作在正侧视情况下的系统参数进行仿真实验[15],成像算法采用精度较高、稳定性较好的BP算法。通常,在点目标参数设置中都将目标RCS值设为恒定值,而此时需要把随频带和方位角变化的RCS值添加到回波模型中,在一个合成孔径时间内,方位向时域各个采样点即对应波束宽度内方位角的变化,距离向频域各个采样点即对应带宽内的频率变化。因此,基于上节12组参数,本文观察对比以中心频点、方位角为参考的恒定RCS(称为恒定RCS)和考虑频带、方位角相关性的RCS(称为相关RCS)的点目标仿真结果,系统仿真参数场景中心斜距为1000 m,脉冲宽度0.25 μs,载频16 GHz,系统带宽和方位波束宽度参数的设置同第3节。
选取其中一组参数△f=2.0 GHz,△ψ=10°为例,点目标仿真对比结果如图 7所示。由于本文的研究内容针对高分辨率SAR辐射定标,因此,可以忽略相位的影响,并只关注辐射定标的相关参数。
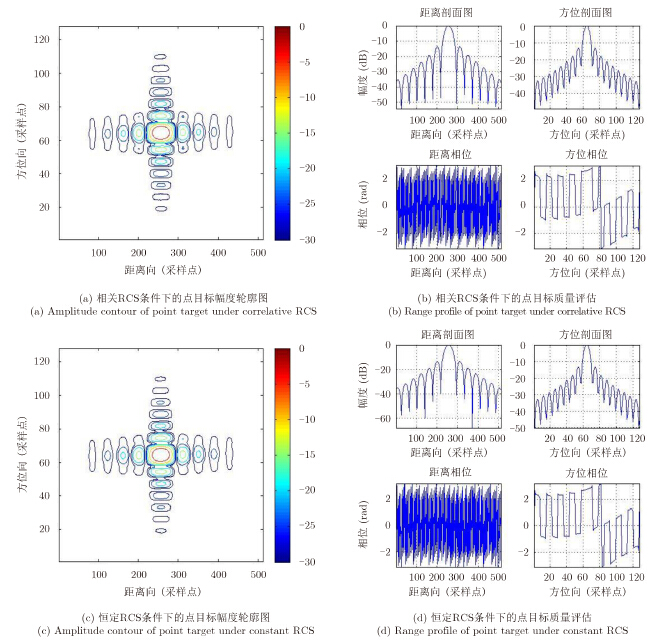
|
图 7 点目标仿真结果对比 Fig.7 Comparison of point target simulation results |
针对3.1节的4组参数进行SAR点目标仿真,分别记录点目标峰值能量、积分能量及距离向和方位向峰值旁瓣比(PSLR)、积分旁瓣比(ISLR) 4个参量如表 1-表 4及图 8所示。
| 表 1 第1组参数点目标仿真结果(dB) Tab. 1 Point target simulation results of the first case (dB) |
| 表 2 第2组参数点目标仿真结果(dB) Tab. 2 Point target simulation results of the second case (dB) |
| 表 3 第3组参数点目标仿真结果(dB) Tab. 3 Point target simulation results of the third case (dB) |
| 表 4 第4组参数点目标仿真结果(dB) Tab. 4 Point target simulation results of the fourth case (dB) |
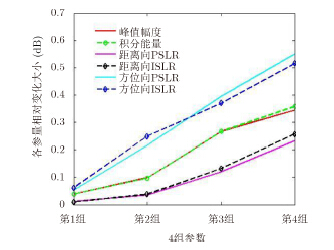
|
图 8 RCS随频带变化的点目标仿真 Fig.8 Point target simulation results of RCS with different bandwidths |
通过上述图表可知,当系统带宽超过2.0 GHz,即相对带宽大于10%时,点目标峰值能量、积分能量的变化超过0.20 dB;当带宽为4.0 GHz时,点目标峰值能量和积分能量的变化已达到0.35 dB。
4.2 RCS随方位角变化的点目标仿真针对3.2节的4组参数进行SAR点目标仿真,分别记录点目标峰值能量、积分能量及距离向和方位向峰值旁瓣比(PSLR)、积分旁瓣比(ISLR) 4个参量如表 5-表 8及图 9所示。
| 表 5 第5组参数点目标仿真结果(dB) Tab. 5 Point target simulation results of the fifth case (dB) |
| 表 6 第6组参数点目标仿真结果(dB) Tab. 6 Point target simulation results of the sixth case (dB) |
| 表 7 第7组参数点目标仿真结果(dB) Tab. 7 Point target simulation results of the seventh case (dB) |
| 表 8 第8组参数点目标仿真结果(dB) Tab. 8 Point target simulation results of the eighth case (dB) |
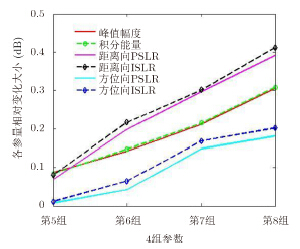
|
图 9 RCS随方位角变化的点目标仿真 Fig.9 Point target simulation results of RCS with different azimuth beamwidths |
通过上述图表可知,当方位波束宽度超过10°时,点目标峰值能量、积分能量的变化大约为0.15 dB;当方位波束为30°时,点目标峰值能量和积分能量的变化已达到0.30 dB。
4.3 RCS随频带和方位角变化的点目标仿真针对3.3节的4组参数进行SAR点目标仿真,分别记录点目标峰值能量、积分能量及距离向和方位向峰值旁瓣比(PSLR)、积分旁瓣比(ISLR) 4个参量如表 9-表 12及图 10所示。
| 表 9 第9组参数点目标仿真结果(dB) Tab. 9 Point target simulation results of the ninth case (dB) |
| 表 10 第10组参数点目标仿真结果(dB) Tab. 10 Point target simulation results of the tenth case (dB) |
| 表 11 第11组参数点目标仿真结果(dB) Tab. 11 Point target simulation results of the eleventh case (dB) |
| 表 12 第12组参数点目标仿真结果(dB) Tab. 12 Point target simulation results of the twelfth case (dB) |
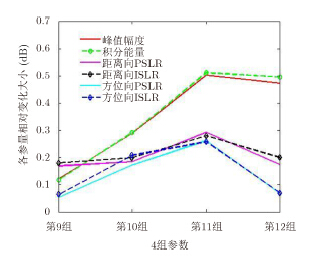
|
图 10 RCS随频带和方位角变化的点目标仿真 Fig.10 Point target simulation results of RCS with different bandwidths and beamwidths |
通过上述图表可知,当△f=1.0 GHz,△ψ= 10°时,点目标峰值能量、积分能量的变化已超过0.2 dB;当系统带宽超过2.0 GHz,方位波束超过20°时,点目标峰值能量和积分能量的变化甚至达到0.5 dB。
综上,随着SAR系统带宽变大和方位波束变宽,点目标的峰值能量和积分能量变化整体呈上升趋势,且已达到辐射定标不可忽略程度;但是,在实际SAR系统中,方位分辨率和距离分辨率不会相差太大,因此,对于4.1节和4.2节的参数仅限于仿真分析;另外,通过对比分析图 8-图 10可以得出,由于最终的SAR图像质量与系统分辨率息息相关,进而会影响点目标峰值能量、积分能量提取,因此,对于工作在不同波段、不同模式、不同参数条件下的高分辨率SAR系统需要视具体情况进行分析。
5 结束语对于高分辨率SAR辐射定标,不仅需要提高参考目标本身的加工精度,同时还需要结合高分辩率条件下的SAR成像特点重新考虑定标模型,改进辐射定标算法。为定量分析大距离带宽和宽方位向波束对参考目标RCS及辐射定标的影响,本文借助FEKO 3维电磁仿真软件,构建三面体角反射器的电磁散射仿真几何模型,采用MLFMM方法获取目标RCS随频带和方位角的变化数据,结合高分辨率SAR点目标仿真,系统分析参考目标RCS的频带和方位角相关性。仿真结果表明,在Ku波段相对带宽超过10%时,上述因素带来的影响超过0.20 dB;在方位波束宽度超过10°,上述影响大约为0.15 dB,必须在实际数据处理中加以校正,这对于参考目标的辐射特性保持和系统质量评估也将提出更高要求。高分辨率SAR参考目标辐射特性校正算法有待进一步研究。
| [1] | Curlander J C. 合成孔径雷达—系统与信号处理[M]. 北京: 电 子工业出版社, 2006: 217-220. Curlander J C. Synthetic Aperture Radar: Systems and Signal Processing[M]. Beijing: Publishing House of Electronics Industry, 2006: 217-220.(  1) 1) |
| [2] | 李震, 廖静娟, 等. 合成孔径雷达地表参数反演模型与方法[M]. 北京: 科学出版社, 2011: 24-33. Li Zhen, Liao Jing-juan, et al.. Synthetic Aperture Radar Surface Parameters Inversion Model and Method[M]. Beijing: Publishing House of Science, 2011: 24-33.(  1) 1) |
| [3] | Khalid E D, Peter M, Desmond P, et al.. Understanding the significance of radiometric calibration for SAR imagery[C]. Canadian Conference on Electrical and Computer Engineering, Toronto, Canada, 2014: 1-6.( 1) 1) |
| [4] | Freeman A. SAR calibration: an overview[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(6): 1107-1123.( 1) 1) |
| [5] | Gray A L, Paris W V, and Charles E L. Synthetic aperture radar calibration using reference reflectors[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(3): 374-382.( 1) 1) |
| [6] | Ulander L M H. Accuracy of using point targets for SAR calibration[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(1): 139-148.( 1) 1) |
| [7] | 邹鲲. 低频UWB-SAR校准技术研究[D]. [博士论文], 国防科学 技术大学, 2005. Zou Kun. Research on low frequency UWB-SAR calibration technique[D]. [Ph.D. dissertation], National University of Defense Technology, 2005.(  1) 1) |
| [8] | 林新越. 高 分辨率SAR参考点目标辐射特性分析与校正方法 研究[D]. [硕士论文], 中国科学院电子学研究所, 2010. Lin Xin-yue. Analysis and calibration method for radiometric characteristics of reference targets in high resolution SAR systems[D]. [Master dissertation], Institute of Electronics, Chinese Academy of Sciences, 2010.(  1) 1) |
| [9] | Bjorn J D, Philipp R L, Matthias J, et al.. Reference target correction based on point-target SAR simulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(3): 951-958.( 1) 1) |
| [10] | Bjorn J D and Marco S. The radiometric measurement quantity for SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(12): 5307-5313.( 1) 1) |
| [11] | 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出 版社, 2010: 16-19. Huang Pei-kang, Yin Hong-cheng, and Xu Xiao-jian. Radar Target Characteristics[M]. Beijing: Publishing House of Electronics Industry, 2010: 16-19.(  1) 1) |
| [12] | Griesser T and Balanis A. Backscatter analysis of dihedral corner reflectors using physical optics and the physical theory of diffraction[J]. IEEE Transactions on Antennas and Propagation, 1987, 35(10): 1137-1147.( 1) 1) |
| [13] | Sarabandi K and Chiu T. Optimum corner reflectors for calibration of imaging radars[J]. IEEE Transactions on Antennas and Propagation, 1996, 44(10): 1348-1361.( 1) 1) |
| [14] | 林新越, 洪峻, 明峰. 高分辨率SAR参考点目标频带调制效应 的校正方法[J]. 国外电子测量技术, 2010, 29(4): 32-36. Lin Xin-yue, Hong Jun, and Ming Feng. A calibration method for frequency modulation of reference targets in high resolution SAR systems[J]. Foreign Electronic Measurement Technology, 2010, 29(4): 32-36.(  1) 1) |
| [15] | Cumming I G and Wong F H. 合成孔径雷达成像—算法与 实现[M]. 北京: 电子工业出版社, 2007: 38-41. Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Beijing: Publishing House of Electronics Industry, 2007: 38-41.(  1) 1) |


