②微波成像技术国家级重点实验室 北京 100190
③中国科学院大学 北京 100049
②National Key Laboratory of Science and Technology on Microwave Imaging, Beijing 100190, China
③University of Chinese Academy of Sciences, Beijing 100049, China
对自然区域,地表覆盖物的分类是生态环境监测的首要内容。多角度合成孔径雷达(SAR)是一种新型遥感信息获取与处理技术,可以对目标进行方位向大角度连续观测。最大连续观测范围可以达到360°,被称为圆周轨迹SAR或圆迹SAR。多角度SAR的主要优势有:在观测各向同性目标时可以获得比条带成像模式更大的多普勒带宽,从而具有更好的分辨率和信噪比[1]。当目标在方位向上存在多个散射中心时,多角度SAR可以获取非各向同性散射信息,反映目标的散射取向变化,用于特征描述和地表覆盖物分类。地物分类是极化雷达在遥感领域中的主要应用之一。地表覆盖物的复杂结构使得后向散射信号包含了混合散射机制,介电性质,形状和体结构信息。因此,引入极化作为常规观测手段的补充对于获取地表覆盖物的特征及分类应用十分必要[2]。全极化SAR数据的优势在于可以利用相干极化散射矩阵合成出任意收发极化状态下目标的散射系数,从而为目标分类提供完备的极化散射信息。利用极化目标分解方法和分类方法可以区分并初步识别不同地表覆盖物的散射机制[3]。因此,多角度观测与全极化观测相结合有利于遥感应用获取更加丰富的目标后向散射信息。
目前,国内外学者在多角度SAR领域的研究还主要集中于成像体制和处理方法方面:Falconer和Moussally在1995年论证了多角度SAR的3维高分辨成像原理[4]。此后,Soumekh和Chan等学者相继发表论文论证了多角度SAR的3维成像原理并给出了仿真结果[5, 6]。法国与瑞典合作在2005年完成了机载多角度SAR飞行实验,获得了P,L个波段的高分辨率3维图像[7]。Oriot等人在2007年利用机载圆迹SAR对尼姆的圆形剧场进行成像,获得了数字高程模型图(DEM)[8]。德宇航在2008年首次完成了基于高精度DEM的L波段全极化圆迹SAR机载实验[9],在高精度快速成像方面取得了突破,图像质量也获得了巨大的提升。同常规条带SAR相比,多角度图像包含了更丰富的地物特征差异,在极化散射特征建模与分类应用方面展现出巨大的研究价值。国内的中科院电子所、中科院空间中心、西电等研究单位也在近年来开展了多角度SAR理论和仿真研究[10, 11, 12]。中科院电子所微波成像技术国家级重点实验室于2011年8月在四川绵阳地区完成了P波段全极化圆迹SAR机载实验,获取了高分辨率全极化图像。数据展现了丰富的地物特征信息和明显的分类应用优势[1]。
在多角度SAR成像过程中,常按方位角间隔分成若干个子孔径进行相干处理,最后再累加获得全孔径图像。若目标对所有孔径都满足各向同性假设,全相干累加处理可以获得分辨率和信噪比最优的图像。然而实际地物的散射特征仅在有限的方位角内保持稳定,甚至在分辨单元内可能存在多种不同类型的散射中心。这对以人造建筑为主要观测对象的单极化功率图像解译而言并不是非常明显。但是对基于极化特征参数的遥感应用,例如变化检测和地物分类,却存在参数估计不准的问题。现有研究表明:基于最大似然比的非各向同性目标检测[13, 14]方法可用于消除条带SAR在农田区域中的非各向同性散射贡献。首先将条带图像(方位角在20°到40°之间)分解成6-8个子孔径。再利用极化相干矩阵计算基于复Wishart分布的假设检验似然比。依据N-P准则,可以自适应地估计恒虚警(CFAR)门限,只保留平稳的子孔径散射贡献。传统的窄方位角成像模式可以忽略非各向同性散射,因为它的多角度散射特征不足以提供有价值的信息。但是多角度观测模式需要进一步拓展现有方法,在保留非各向同性散射贡献的基础上挖掘消除过程产生的信息。
本文与现有方法的主要区别在于:本方法的核心是把不同类型的信息分开处理,目标的非各向同性散射信息可以通过消除过程产生的特征来展现,发挥多角度观测的特色优势。此外,现有方法使用的似然比统计量在子孔径散射变化较大时易导致恒虚警判决函数饱和,且估算门限需要依赖数值解法。有研究表明:可以利用子孔径间的相对极化熵变化来代替似然比判决,以避免计算效率的问题[15]。然而该方法仅以农田区域为观测对象,缺乏关联极化熵和似然比参数的散射机理分析,且失去了恒虚警门限估计能力。针对现有研究情况,本文的主要工作包括:优化了假设检验问题以降低似然比统计量动态范围;分析了相干斑影响以及两类散射媒质在消除过程中的极化熵变化机理;利用虚警概率分布函数的单调性降低了计算复杂度。综合上述3个方面的工作,本文提出了多角度极化SAR图像中的非各向同性散射估计与消除方法。使用机载P波段极化圆迹SAR数据进行了特征分析,验证了方法的有效性。
论文第2节针对多角度观测特点优化了最大似然比检验统计量,第3节分析了相干斑对似然比和极化熵的影响,并初步给出了非各向同性散射消除过程的内在机理,第4节完成了处理流程及单调性证明,第5节通过机载试验结果证明本文算法能够检测子孔径中的非各向同性散射贡献,分析验证了消除处理前后的散射特征变化机理。
2 非各向同性散射检测与条带图像在频域上的子孔径分解不同,多角度SAR子孔径图像序列是在时域上选择有限方位角范围内的原始回波数据直接生成的[9]。如果拥有成像区域的高精度DEM以及雷达天线准确的位置信息,还可以直接生成投影在地理坐标系上的子孔径影像。常用的目标极化特征数据表达形式包括散射系数矩阵、极化相干矩阵以及极化协方差矩阵。由于独立样本的散射矩阵矢量和对相干斑抑制没有贡献,本文选用极化相干矩阵作为分析建模的表达工具。
现有研究已经证明,独立同分布单元的散射矢量可通过服从多变量复高斯分布N3(0,S)的散射矢量进行表征。其n视3×3极化相干矩阵A=n·T可被证明服从复Wishart分布W3(n,S)[16],S为散射矢量的复协方差矩阵。由此可得n视极化相干矩阵的概率密度函数为:
| ${{p}^{n}}(T|\sum )=\frac{{{n}^{3n}}|T{{|}^{n-3}}\exp [-n\text{Tr}({{\sum }^{-1}}T)]}{K(n,3)|\sum {{|}^{n}}}$ | (1) |
| $K(n,3)={{\pi }^{3}}\Gamma \left( n \right)\Gamma \left( n-1 \right)\Gamma \left( n-2 \right)$ | (2) |
如果R个子孔径相干矩阵Ti,i=1,2,···,R满足独立同分布条件,可建立以下假设:
| $\left. \begin{array}{*{35}{l}} {{\text{H}}_{0}}:{{\sum }_{1}}={{\sum }_{2}}=\cdots ={{\sum }_{R}}=\sum \\ {} \\ {{\text{H}}_{1}}:{{\sum }_{i}}={{\sum }_{\text{A}}}\ne {{\sum }_{j}}={{\sum }_{\text{B}}};\quad i\in {{R}_{\text{A}}},j\in {{R}_{\text{B}}} \\ \end{array} \right\}$ | (3) |
| $L(\sum )=\prod\limits_{k=1}^{{{N}_{\text{A}}}}{p({{A}_{k}}|\sum )}\cdot \prod\limits_{k=1}^{{{N}_{\text{B}}}}{p({{A}_{k}}|\sum )}\\ \qquad\ \ =\frac{{{n}^{3n({{N}_{\text{A}}}+{{N}_{\text{B}}})}}}{K{{(n,3)}^{{{N}_{\text{A}}}+{{N}_{\text{B}}}}}}\cdot \frac{1}{{{\left| \sum \right|}^{n{{N}_{\text{A}}}+n{{N}_{\text{B}}}}}}\cdot \prod\limits_{k=1}^{{{N}_{\text{A}}}+{{N}_{\text{B}}}}{{{\left| {{A}_{k}} \right|}^{n-3}}}\\ \qquad\ \ \quad \cdot \exp \left( -n\cdot \text{Tr}\left( {{\sum }^{-1}}\cdot \sum\limits_{k=1}^{{{N}_{\text{A}}}+{{N}_{\text{B}}}}{{{A}_{k}}} \right) \right)$ | (4) |
| $L({{\sum }_{\text{A}}})\cdot L({{\sum }_{\text{B}}})=\prod\limits_{k=1}^{{{N}_{\text{A}}}}{p({{A}_{k}}|{{\sum }_{\text{A}}})}\cdot \prod\limits_{k=1}^{{{N}_{\text{B}}}}{p({{A}_{k}}|{{\sum }_{\text{B}}})} \\ \qquad\ \ \qquad\ \ \qquad =\frac{{{n}^{3n({{N}_{\text{A}}}+{{N}_{\text{B}}})}}}{K{{(n,3)}^{{{N}_{\text{A}}}+{{N}_{\text{B}}}}}}\cdot \frac{1}{{{\left| {{\sum }_{\text{A}}} \right|}^{n{{N}_{\text{A}}}}}{{\left| {{\sum }_{\text{B}}} \right|}^{n{{N}_{\text{B}}}}}} \\ \quad \qquad\ \ \qquad\ \ \qquad \prod\limits_{k=1}^{{{N}_{\text{A}}}+{{N}_{\text{B}}}}{{{\left| {{A}_{k}} \right|}^{n-3}}}\cdot \exp (-n\cdot \text{Tr}(\sum _{\text{A}}^{-1} \\ \quad \qquad\ \ \qquad\ \ \qquad \cdot \sum\limits_{k=1}^{{{N}_{\text{A}}}}{{{A}_{k}}}+\sum _{\text{B}}^{-1}\cdot \sum\limits_{k=1}^{{{N}_{\text{B}}}}{{{A}_{k}}}))$ | (5) |
| ${{\wedge }_{\text{AB}}}=\frac{L(\sum\limits_{{}}^{\wedge }{{}})}{L({{\sum\limits_{{}}^{\wedge }{{}}}_{\text{A}}})\cdot L({{\sum\limits_{{}}^{\wedge }{{}}}_{\text{B}}})}={{\left( \frac{{{\left| {{\sum\limits_{{}}^{\wedge }{{}}}_{\text{A}}} \right|}^{{{N}_{\text{A}}}}}{{\left| {{\sum\limits_{{}}^{\wedge }{{}}}_{\text{B}}} \right|}^{{{N}_{\text{B}}}}}}{{{\left| {{\sum\limits_{{}}^{\wedge }{{}}}_{\text{T}}} \right|}^{{{N}_{\text{T}}}}}} \right)}^{n}}$ | (6) |
相干斑是由SAR相干累加处理引起的固有特点,对图像的统计特性以及极化特征参数估计都存在影响。为此,需要分别针对似然比和极化熵参数来分析。从图像统计处理的角度来看,相干斑可以由乘性噪声模型来表征。由于SAR在获取数据时常使采样间隔大于空间分辨率,因此相邻像素间往往具有一定的相关性。当相干斑存在空间相关性时,处理窗口内的独立样本数量往往小于实际样本数。由式(6)可知,独立样本数量n应采用等效视数(ENL)估计值,若直接使用样本数作为独立样本数量可能会导致似然比检验统计量被高估。对于均匀区域,功率图像的等效视数ENL可以被定义为:
| ${\rm{ENL}} = 1/{\tau ^2}$ | (7) |
| ${{\wedge }_{\text{AB}}}=\frac{{{\left| {{\sum\limits_{{}}^{\wedge }{{}}}_{\text{A}}} \right|}^{{{N}_{\text{A}}}\text{EN}{{\text{L}}_{\text{A}}}}} \ {{\left| {{\sum\limits_{{}}^{\wedge }{{}}}_{\text{B}}} \right|}^{{{N}_{\text{B}}}\text{EN}{{\text{L}}_{\text{B}}}}}}{{{\left| {{\sum\limits_{{}}^{\wedge }{{}}}_{\text{T}}} \right|}^{{{N}_{\text{T}}}\text{EN}{{\text{L}}_{\text{T}}}}}}$ | (8) |
极化熵是信息熵的一种,用于度量极化散射矢量中3种本征极化散射类型在统计意义上的无序性,值域范围在[0, 1]之间。如式(9)所示,熵值越高则代表3种本征极化散射类型的无序性越强,描述散射特征所需的信息量越多。例如森林区域以体散射为主,电磁波在多次散射过程中与不同取向的粒子云发生作用,需要3组正交极化矢量才能对其进行完整描述。低熵则代表观测对象仅存在1种主要的本征极化散射类型,其散射贡献远远大于其它两种散射类型。例如海洋以表面散射为主,采用1维极化散射矢量就足以描述它的全部信息。由于极化熵计算仅依赖极化相干矩阵的特征值,因此对由方位角变化引起的极化基变化不敏感,有利于在多角度观测模式中弱化地形方位向变化引起的特征变化。
| $H = - \sum\limits_{k = 1}^3 {{P_k}{{\log }_3}({P_k})} $ | (9) |
由于相干斑会直接影响极化相干矩阵特征值分解的结果,因此在理论上必然会造成极化熵估计误差。基于其概率密度函数可以证明样本特征值估计的渐进无偏性。通过样本特征值的渐进最大似然估计,可以建立真实特征值lk与样本估计值λk之间的数值关系[17]:
| ${\lambda _k} = {l_k} + \frac{{{l_k}}}{N}\sum\limits_{j \ne k}^3 {\frac{{{l_j}}}{{{l_k} - {l_j}}}} + O\left( {{N^{ - 1}}} \right),\quad k = 1,2,3$ | (10) |
由式(10)可知,独立样本数量N反映了平均程度,该值越大则样本特征值误差越小。通常采用9×9以上的窗口可以获取可靠的极化熵估计。但为了维持足够高的几何分辨率,对单景极化SAR影像处理时往往难以使用大窗口平均处理来获得准确的特征值估计。另一方面,较大的平均窗口易导致不同散射特性的样本也参与平滑,从而增加了3种本征极化散射类型的无序性,造成极化熵被高估。
3.2均匀媒质情况均匀媒质在R个子孔径内具有近似各向同性的散射特征,较接近式(3)中的零假设条件。此时式(8)更接近于1,低于判决门限的概率很小。对被判决为各向同性的子孔径散射贡献可以进行累加,一方面可以获得最佳的分辨率和信噪比,另一方面可以增大式(10)中的独立样本数量N以降低样本特征值估计误差。由于平滑过程是在同一分辨单元内不同子孔径之间进行,因此可以维持原有的空间分辨率。例如本文对单个子孔径影像采用3×3窗口进行平滑,那么当被判决为各向同性的子孔径数量达到9个,就可以满足极化熵的估计要求。这是普通的条带SAR影像难以做到的。最大似然比判决将混叠非各向同性散射的可能性控制在恒定的虚警概率以内。由此可见,均匀媒质极化熵降低是与消除非各向同性散射(即式(8)更接近于1)过程存在内在联系的。
3.3非均匀媒质情况非均匀媒质在R个子孔径内的散射差异较大。特别是某些人造目标可能仅在10°~20°连续的方位角范围内有较强的同性后向散射。构成非均匀媒质的特征组合也比均匀媒质更复杂,需要考虑每个等效散射中心的极化熵,子孔径间的功率比例和相似性分布等因素。因此在消除非各向同性散射的过程中,难以简单地认为极化熵一定会降低。例如部分人造结构可能在多角度观测中仅有1个孔径存在较强的后向散射贡献,在其它孔径中则缺乏低熵散射类型或以体散射为主。后向散射较强的子孔径具有非常低的极化熵,且其较大的功率使其在原始全孔径累加影像中占主要贡献,平均极化熵也更接近该子孔径的极化熵值。基于似然比最大化原则,少数低熵子孔径将被优先消除。消除非各向同性散射之后,累加和的功率会明显降低,剩余的孔径将以平均体散射为显性极化表征,极化熵也因此比消除前更大。由此可见,消除多角度非各向同性散射贡献并不能直接等效为降低了极化特征组合的无序性。因此,消除非各向同性散射后的极化熵并不是必然降低的,其变化趋势应与多散射中心目标的结构有关。
4 非各向同性散射检测与消除方法 4.1恒虚警判决根据Neyman-Pearson准则,H0假设成立的判决条件是:
| $\wedge >{{c}_{\beta }},\quad {{P}_{\text{fa}}}({{c}_{\beta }})=P(\wedge \le {{c}_{\beta }};{{\text{H}}_{0}})$ | (11) |
| $\wedge =\max \left\{ {{\wedge }_{\text{mean}\left( \sum\limits_{j\ne i}^{R}{j} \right),i}};\quad i,j=1,2,\cdots ,R \right\}$ | (12) |
| ${{P}_{\text{fa}}}({{c}_{\beta }})=1-\int_{-\infty }^{-\rho \log {{c}_{\beta }}}{{{p}_{-\rho \log \text{ }\wedge }}(x)\text{d}x}\\ \approx 1-{{\gamma }_{\text{inc}}}(f/2,-\rho \log {{c}_{\beta }}) \\ \quad -{{\omega }_{2}}[{{\gamma }_{\text{inc}}}(f/2+2,-\rho \log {{c}_{\beta }}) \\ \quad -{{\gamma }_{\text{inc}}}(f/2,-\rho \log {{c}_{\beta }})]$ | (13) |
| $f = 9 \cdot (R - 1),\quad \rho = 1 - \frac{{51}}{{6f}}\left[{\frac{1}{{{N_i}}} + \frac{1}{{{N_{\rm{T}}} - {N_i}}} - \frac{1}{{{N_{\rm{T}}}}}} \right]$ | (14) |
| $\begin{aligned} {\omega _2} = & \frac{9}{{4{\rho ^2}}}\left( {\frac{4}{3}\left[{\frac{1}{{{N_i}^2}} + \frac{1}{{{{\left( {{N_{\rm{T}}} - {N_i}} \right)}^2}}} - \frac{1}{{N_{\rm{T}}^2}}} \right]} \right.\\ & - {{{(1 - \rho )}^2}(R - 1)} \bigg) \end{aligned} \hspace{35pt}$ | (15) |
| ${\gamma _{{\rm{inc}}}}(a,x) = \frac{1}{{\Gamma \left( a \right)}}\int_0^x {{{\rm{e}}^{ - t}}{t^{a - 1}}{\rm{d}}t} $ | (16) |
由于所求未知数是不完全伽玛函数的积分上限,因此式(13)仍然需要数值解法来计算,对计算效率和精度的影响较大。本文建议通过式(13)的单调性来完成判决,而无需计算门限后再判决。由式(16)可知ginc(a,x)为单调递增函数,即有:
| ${\gamma _{{\rm{inc}}}}(a,{x_2}) > {\gamma _{{\rm{inc}}}}(a,{x_1}),\,\forall {x_2} > {x_1} > 0$ | (17) |
| $\begin{array}{l} {P_{{\rm{fa}}}}\left( {{x_2}} \right) - {P_{{\rm{fa}}}}\left( {{x_1}} \right)\\ \quad \approx \left( {{\omega _2} - 1} \right)\left( {{\gamma _{{\rm{inc}}}}\left( {f/2,{x_2}} \right) - {\gamma _{{\rm{inc}}}}\left( {f/2,{x_1}} \right)} \right)\\ \quad \quad + {\omega _2}\left[{{\gamma _{{\rm{inc}}}}\left( {f/2 + 2,{x_1}} \right) - {\gamma _{{\rm{inc}}}}\left( {f/2 + 2,{x_2}} \right)} \right] \end{array}$ | (18) |
| ${\omega _2} \approx \frac{3}{{N_i^2}}$ | (19) |
| $0 \lt {\omega _2} \lt 1$ | (20) |
| ${P_{{\rm{fa}}}}({x_2}) - {P_{{\rm{fa}}}}({x_1}) \lt 0$ | (21) |
| ${{P}_{\text{fa}}}(-\rho \log \wedge )>{{P}_{\text{fa}}}(-\rho \log {{c}_{\beta }})=\beta $ | (22) |
基于上述分析,可以建立一种非各向同性散射估计与消除方法,用于获得满足各向同性散射累加的多角度极化SAR图像。若数据集包含R景多角度子孔径影像,成像区域内每个采样位置处的像素都需要通过以下步骤循环迭代,以消除不满足各向同性假设的散射贡献。
步骤1 判断是否满足迭代停止条件,若满足条件则执行步骤5,不满足则执行步骤2;停止条件是满足R=4,该条件可以保证式(19)成立且避免由虚警及复杂散射现象造成的过度消除问题;
步骤2 对每个像素位置使用式(8)在3×3统计窗口内计算的似然比检测量LAB,循环R次;
步骤3 使用式(12)获得最大值L及其所属子孔径subj;
步骤4 使用式(13)计算Pfa(-rlog∧)并通过式(22)判断各向同性假设是否成立,若成立则执行步骤5,否则消除子孔径subj在该像素位置的散射贡献,令R=R-1,执行步骤1;
步骤5 做子孔径累加,计算极化相干矩阵并输出。
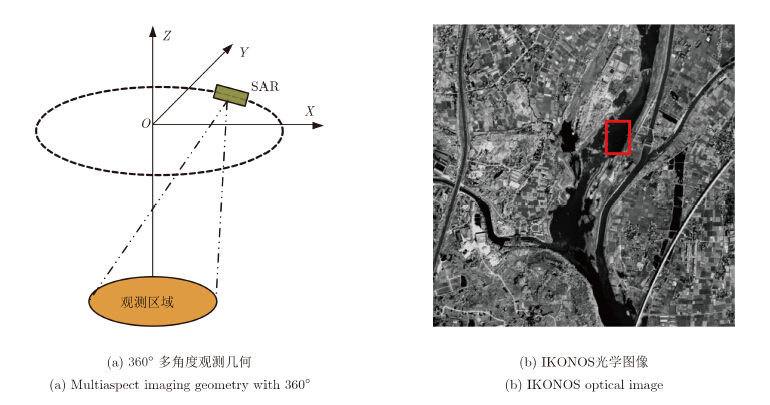
5 机载数据试验结果及分析本文使用的试验数据是中科院电子所于2011年8月在四川绵阳地区利用机载P波段全极化SAR获取的国内首幅360°多角度观测图像,试验参数可参见表 1。试验的观测几何和观测场景光学影像如图 1所示,包含有水体、农田、森林、公路、铁路、输电网络和建筑物等对象。为满足大部分目标的各向同性散射假设,首先利用后向投影算法生成每景方位角为36°的子孔径影像,因此共有10景子孔径影像。处理过程包括了成像处理、运动补偿、旁瓣抑制及极化定标等步骤,具体的处理方法可以参考文献[1, 9]。影像坐标系为WGS-84,像素样本间隔为1 m×1 m,共2001行×2001列个像素。
| 表 1 中科院电子所圆迹SAR飞行试验主要参数 Tab. 1 IECAS CSAR experiment parameters |
|
图 1 试验观测几何与场景 Fig.1 Experiment imaging geometry and scene |
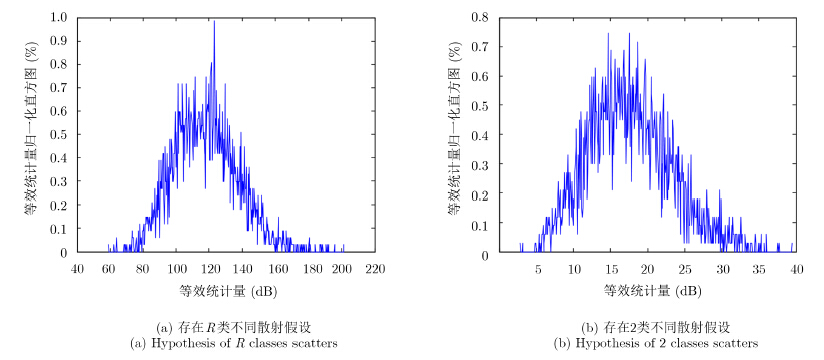
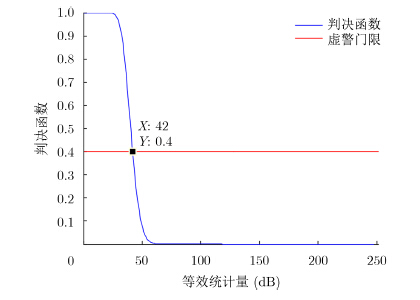
从观测场景中选取一块76×44个像素的树林区域,用于对比现有方法[14]和本文方法在值域范围上的差异。此外,通过该数据还可以证明本文使用的统计量处于恒虚警判决函数敏感区。由图 2可知,若依据现有方法假设存在R类不同散射贡献来计算似然比等效统计量-rlog∧,其值域在[60, 200]之间。而依据本文似然比计算的等效统计量值域在[5, 40]之间。依据两种统计量对同一数据计算的判决函数值域范围存在明显差异,这对判决式(22)的结果和有效性都具有直接影响。将本文试验数据参数代入式(13),可以将似然比等效统计量映射为判决函数,如图 3中的蓝色曲线所示。图中的红线是式(22)中的恒虚警率门限,在本文中设置为β=0.4,所对应的等效统计量为42 dB。该图表明判决函数在[10, 60]之间是单调递减的敏感区,其余部分则是饱和区。这意味着若等效统计量值域范围在判决函数饱和区内,则恒虚警率门限取任何值都不会改变判决结果,即判决函数失效。图 2(a)中的值域范围就完全处于饱和区,所有像素都被判定为非各向同性散射。图 2(b)表明,若对树林区域使用本文给出的似然比等效统计量,其值域范围将完全处于敏感区,在β=0.4条件下可以判定该区域全部像素都满足各向同性假设(小于42 dB)。该结果与对树林区域多角度观测的散射特征研究结论相符[19]。若提高虚警门限则会增加非各向同性散射像素的数量,该结果符合虚警概率的物理含义。虚警概率β=0.4的取值是通过主观判断获得的。由于虚警概率与检测概率成正比,使用者可以在不同虚警概率条件下,观察所关注的重点目标是否能够被完整地检测到。在此基础上,选择最小值作为虚警概率计算判决门限。
|
图 2 似然比等效统计量归一化直方图 Fig.2 The normalized histogram of equivalent likelihood ratio statistic |
|
图 3 判决函数及恒虚警率门限 Fig.3 The judging function and CFAR threshold |
经过迭代消除后,可以获得全孔径累加的极化相干矩阵,其Pauli基伪彩色影像如图 4所示。首次迭代时,由式(13)计算的判决函数如图 5(a)所示,其中的水体、树林及部分农田区域的等效统计量比较强,反映出上述区域偏向于各向同性散射。而人造目标区域则更偏暗,显示其偏向于非各向同性的散射特征。此外,图像在值域[0, 1]之间的灰度变化连续性较好,表明本文提出的等效统计量动态范围合理,可以充分反映不同散射类型区域间的差异性。与该图相比,在最终迭代图(图 5(b))中由暗变亮的区域表示消除处理提升了该区域的似然比,达到了各向同性散射判决条件。此类区域大部分为地形叠掩及农田区域。影像底部的河流西岸区域有面向东北向及东向的大面积山坡,部分区域在某些观测角度下发生了叠掩现象。通过消除非各向同性散射,最终的全孔径累加图像在一定程度上弱化了叠掩散射能量,使得该区域的主要散射特征来自于未发生叠掩的观测角度,如图 6(b)所示。此外,农田区域的地垄构造在某些观测角度下与SAR入射波发生了较强的谐振[14]。在处理过程中,由于发生谐振的子孔径散射与其它大部分没有发生谐振的子孔径差异最大,因此在迭代过程中被逐步消除了。在最终迭代判决函数图中也存在一些比水体暗但又不属于深黑色的区域。这部分区域虽然在不同观测角度下的散射过程并不是非常平稳,但仍未达到判决门限。这部分目标主要以农田和树林区域为主。

|
图 4 消除非各向同性散射贡献后的Pauli彩图 Fig.4 The Pauli color image after removing the anisotropic subapertures |

|
图 5 判决函数图 Fig.5 The judging function image |
|
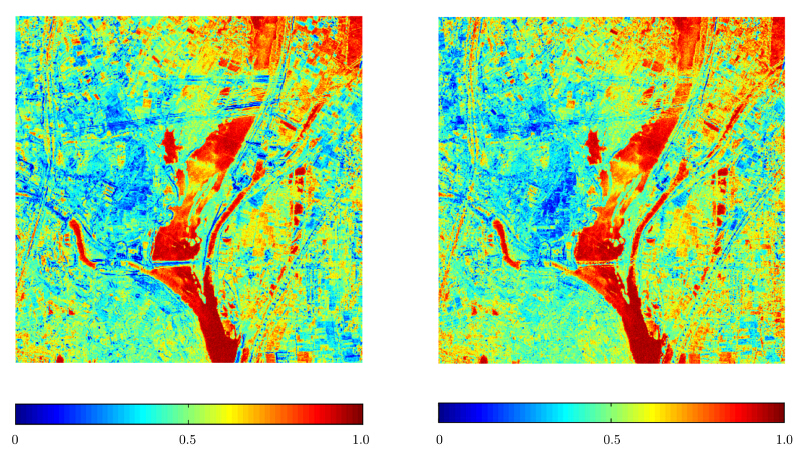
图 6 极化熵图 Fig.6 The polarimetric entropy image |
在消除非各向同性散射后,本文将分析消除前后同一区域的极化熵(式(9))变化,样本窗口均为3×3。图 6(a)是利用原始的全孔径累加数据计算的极化熵,图 6(b)是消除后的结果。为了更直观地分析消除前后极化熵的变化,计算消除后极化熵减去消除前极化熵的差值图。图 7中的极化熵在[-0.6,0.8]之间,变化范围较大。图中心是大片水体,河流上半部西侧还有树林。这些区域在P波段数据中都属于各向同性散射,因此不会通过本文的处理产生极化熵变化。在发生较大变化的像素中,负值(蓝色区域)表示校正后极化熵降低,集中分布在农田区域,表明上述区域内一些非主要方向的散射贡献被消除,降低了全孔径累加后3种本征散射类型的无序程度。正值(黄色及红色区域)表示校正后极化熵增高,分布在人造目标、部分农田和山坡叠掩区域。在上述区域内,被消除的散射贡献在功率比例上占优,极化散射特征组成更单一。因此在消除后却反而增加了3种本征散射类型的无序程度。由此可见,消除非各向同性散射贡献后,极化熵升降与否还取决于观测对象本身随方位角变化的散射特征,并非总是降低。这表明非均匀媒质的极化特征和多角度观测特征所包含的信息存在互补性,可联合描述目标的散射特征。
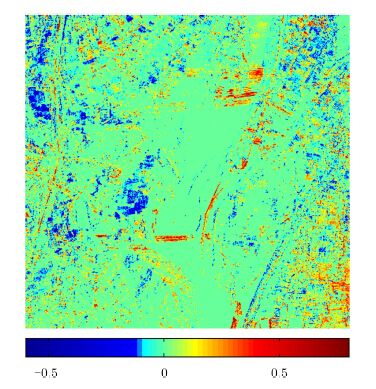
|
图 7 消除非各向同性散射贡献前后的极化熵变化图 Fig.7 The polarimetric entropy changing image before and after removing the anisotropic subapertures |
首次消除的子孔径标号如图 8(a)所示。深红色代表各向同性区域,其它颜色分别代表不同的子孔径标号。图像左下角的环形目标(图 8(c))是由1个蓄水池的池壁与地表构成二面角产生的,如图 8(d)所示。由于每1个子孔径内的强点位置都与观测方向一致,因此能够近似表示不同颜色所对应的子孔径方位角范围。图 8(a)展示出非各向同性散射体的主要方向性散射特征。例如建筑物区域的外墙轮廓展现出明显的方向性信息,从颜色便可以知道墙体的走向。此外,部分建筑物的拱形房顶显示出交替变化的颜色,代表其对称性的散射结构。与之类似的还有梯田的边缘以及河岸防护坡,都在清晰的覆盖区域内带有显著且一致的方向性特征。但第2次消除后,在相同的覆盖范围内却表现为各向同性散射或存在来自于多个方向的散射贡献。这说明此类目标的主要或唯一方向性散射贡献来自于第1次消除的孔径方向。而部分农田区域则会在消除过程中持续展现出清晰的区域性特点,但区域的范围会出现明显变化,如图 8(b)所示。由此可见,消除过程所产生的散射方向特征图具有对多散射中心目标的区分能力,可进一步应用于地物分类。

|
图 8 依据消除过程生成的散射方向特征图 Fig.8 The scattering signature image generated by the removing procedure |
多角度观测体制为极化特征参数估计提供了比常规条带观测更充分的样本数量,因此可以获得更准确的极化特征参数估计。另一方面,多角度观测还可以获取目标的非各向同性散射特征。然而,这两方面的优势需要在处理过程中对非各向同性散射贡献进行区分才能被保持和发挥,否则多个不同类型的散射贡献彼此结合反而会降低参数估计的可信度,也无法为分离方位角上的等效散射中心提供依据。为此,本文提出了多角度极化SAR图像中的非各向同性散射估计与消除方法。利用机载P波段多角度极化数据,本文验证了检验统计量与消除方法的有效性,给出了针对消除机理分析结论的实例,揭示了多角度观测特征与极化特征联合应用的潜力,对后续研究工作的开展具有一定的参考价值。
致谢 感谢中科院电子所的梁兴东研究员、陈龙永博士及机载SAR系统组成员在飞行试验数据获取中提供的帮助和支持。| [1] | Lee J S, Grunes M R, Pottier E, et al.. Unsupervised terrain classification preserving polarimetrics catteringcharacteristics[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4): 722-731.( 3) 3) |
| [2] | Pottier E. Unsupervised classification scheme and topography derivation of PolSAR data based on the H/A/a polarimetric decomposition theorem[C]. Proceedings 4th International Workshop Radar Polarimetry, Nantes, France, 1998: 1-4.( 1) 1) |
| [3] | Falconer D G and Moussally G J. Tomographic imaging of radar data gathered on a circular flight path about a threedimensional target zone[J]. SPIE, 2487: 2-12.( 1) 1) |
| [4] | Soumekh M. Reconnaissance with slant plane circular SAR imaging[J]. IEEE Transactions on Image Processing, 1996, 5(8): 1252-1265.( 1) 1) |
| [5] | Chan T K, Kuga Y, and Ishimaru A. Experimental studies on circular SAR imaging in clutter using angular correlation function technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2192-2197.( 1) 1) |
| [6] | Hubert M. Airborne SAR imaging along a circular trajectory[C]. Sixth European Conference on Synthetic Aperture Radar, Dresden, Germany, 2006: 1–4.( 1) 1) |
| [7] | along a circular trajectory[C]. Sixth European Conference on Synthetic Aperture Radar, Dresden, Germany, 2006: 1-4. Oriot H and Cantalloube H. Circular SAR imagery for urban remote sensing[C]. Seventh European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2008: 1-4.( 1) 1) |
| [8] | Ponce O, Prats-Iraola P, Pinheiro M, et al.. Fully polarimetric high-resolution 3-D imaging with circular SAR at L-band[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3074-3090.( 1) 1) |
| [9] | Lin Y, Hong W, Tan W, et al.. Extension of range migration algorithm to squint circular SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 651-655.( 3) 3) |
| [10] | 张祥坤. 高分辨率圆迹合成孔径雷达成像机理及方法研究[D].[博士论文], 中国科学院空间科学与应用研究中心, 2007. Zhang Xiang-kun. Study on imaging mechanism and algorithm of high-resolution circular SAR[D]. [Ph.D. dissertation], Center for Space Science and Applied Research Chinese Academy of Sciences, 2007.(  1) 1) |
| [11] | 刘燕, 吴元, 孙光才, 等. 圆轨迹SAR快速成像处理[J]. 电子与 信息学报, 2013, 35(4): 852-858. Liu Yan, Wu Yuan, Sun Guang-cai, et al.. Fast imaging processing of circular SAR[J]. Journal of Electronics & Information Technology, 2013, 35(4): 852-858.(  1) 1) |
| [12] | Runkle P, Nguyen L, McClellan J, et al.. Multi-aspect target detection for SAR imagery using hidden Markov models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 46-55.( 1) 1) |
| [13] | Ferro-Famil L, Reigber A, Pottier E, et al.. Scene characterization using subaperture polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(10): 2264-2276.( 1) 1) |
| [14] | 吴婉澜, 王海江, 皮亦鸣. 基于子孔径分析的极化散射机理研究[J]. 雷达科学与技术, 2008, 6(4): 273-277. Wu Wan-lan, Wang Hai-jiang, and Pi Yi-ming. Study on polarimetric scattering bechavior based on subaperture analysis[J].Radar Science and Technology, 2008, 6(4): 273-277.(  5) 5) |
| [15] | Lee J S, Grunes M R, and Kwork R. Classification of multilook polarimetric SAR imagery based on complex Wishart distribution[J]. International Journal of Remote Sensing, 1994, 15(11): 2299-2311.( 1) 1) |
| [16] | Lopez-Martinez C, Pottier E, and Cloude S. Statistical assessment of eigenvector-based target decomposition theorems in radar polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(9): 2058-2074.( 1) 1) |
| [17] | 王海江, 皮亦鸣, 杨小波. 极化SAR图像中基于子孔径分析的两种非平稳目标检测[J]. 成都信息工程学院学报, 2012, 27(3): 243-246. Wang Hai-jiang, Pi Yi-ming, and Yang Xiao-bo. Two kinds of nonstationary targets detection in Pol-SAR images based on subaperture analysis[J]. Journal of Chengdu University of Information Technology, 2012, 27(3): 243-246.(  1) 1) |
| [18] | Ulaby F T, Moore R K, and Fung A [19] K. Microwave Remote Sensing Active and Passive-Volume II: Radar Remote Sensing and Surface Scattering and Emission Theory[M]. USA: Addison-Wesley Publishing Company Advanced Book Program/World Science Division, 1982: 87-106."( 1) 1) |


