合成孔径雷达(Synthetic Aperture Radar,SAR)作为一种主动微波遥感手段,具有全天时全天候工作的能力,能够获取地表的高分辨2维图像。SAR已广泛应用于资源勘查、灾害监测、海洋观测、精细农业、地质测绘等领域,是对地观测的最重要手段之一。
1978年,第1颗星载SAR SEASAT发射成功,以25 m的分辨率对地球表面一亿两千万平方公里的面积进行了测绘,获得了从未有过的陆地、海洋和冰川等数据,开辟了SAR对地观测的新时代。经过几十年的迅猛发展,星载SAR技术日趋成熟,在轨和在研的星载SAR多已具备高分辨率、多极化、多波段、多工作模式等能力。
随着SAR应用领域的不断拓宽和深入,越来越多的观测任务对SAR的性能指标提出了更为苛刻的要求,例如军事侦察、灾害监测等应用,不仅有一定的分辨率要求,更重要的是,在瞬时覆盖度、连续观测范围及3维精确定位等方面有着较高的要求。当前遥感卫星轨道高度一般在600~800 km,由于轨道高度较低,难以满足上述要求,主要体现在:
(1) 瞬时覆盖度小,重访时间长,难以实现对热点区域的快速响应
以轨道高度800 km为例,卫星对地球表面的瞬时覆盖度仅为11.8%,且天线可视范围只能跟随卫星轨道规律地在地面移动,卫星重访时间又通常长达若干天,难以实现对热点地区的快速响应。缓解这一问题的主要思路是利用多颗卫星构建卫星组网来缩短重访时间,例如,意大利的Cosmo-skymed星座由4颗分布在同一轨道内的低轨卫星组成[1],其在紧急操作模式下,响应时间仍需6~18 h,不能从根本上解决响应速度问题。
(2) 波束覆盖面积小,过顶时间短,难以实现大面积区域的连续监测
低轨SAR的波束覆盖面积小,一次成像的测绘带宽一般为几十公里,即使采用以损失分辨率为代价的ScanSAR扫描模式,测绘带宽也仅扩大数倍,此外,低轨SAR过顶时间短,通常为几分钟,对目标的有效观测时间更短,往往只有数秒,上述两个因素制约了低轨SAR对大面积区域的连续监视能力,对于瞬息万变的战场和突如其来的灾害来说,缺少实际应用价值。
(3) 只能获取2维图像,难以实现目标的精确定位和打击
单颗星载SAR一次只能获取一幅2维图像,即3维地物在2维斜距平面上的投影图像,目标信息量少且存在图像畸变,无法确知其在3维空间中的精确位置。为获得观测区域的高程信息,主要技术手段是星载干涉SAR和星载多基线层析SAR。星载干涉SAR采用单星重轨或双星单航过来获得地表的干涉测量数据,反演地形高程,但其只具备地表测高能力,不具备高程向的分辨能力,且对孤立目标、高程突变区域,效果并不理想。星载多基线层析SAR利用单星多次重复飞行形成多条基线,通过层析成像获得3维分辨图像,但其主要局限在于工作效率低,首先该模式对基线分布的要求较高,需要大量的航线样本,例如DLR在利用TerraSAR数据进行3维重建时[2],航迹样本数达上百条,实际使用仅为25条,此外,由于跨行向分辨率通常远低于其他2维分辨率,需要采用计算复杂度极高的稀疏处理方法,这两方面因素使得星载多基线层析SAR难以投入对于时效性有较高要求的应用。
地球同步轨道圆迹SAR (Geosynchronous Circular SAR,Geo-CSAR)将地球同步轨道星载SAR和圆迹SAR巧妙结合,通过轨道参数设计,在距地36000 km高空形成圆形的卫星轨迹,使SAR载荷的大面积区域连续观测成像模式成为可能。Geo-CSAR综合了GeoSAR和CSAR的优势,一方面,因地球同步轨道高度高,其在重复观测周期、测绘带宽和可视能力等方面的性能是低轨SAR无法比拟的,另一方面,360°圆形观测几何不仅能对可视范围内的重点区域进行凝视观测,还能够获取观测场景的散射中心在3维空间中的分布,实现目标的精确3维定位。因此,Geo-CSAR可有效弥补现有低轨SAR的局限性,在全球性的军事侦察、灾害监测等方面具有巨大的应用潜力。
本文首先介绍了Geo-CSAR的研究背景,然后对Geo-CSAR的概念进行了研究,包括Geo-CSAR的轨迹生成和2维、3维分辨率理论,并根据典型参数,结合仿真分析了其成像能力,最后,对Geo-CSAR从概念面向应用需要突破的关键技术进行了讨论。
2 研究背景 2.1 圆迹SAR简介圆迹SAR是近年来发展起来的一种高分辨3维成像模式,通过雷达平台围绕观测区域作圆周运动,获取被观测场景的全方位信息,以满足越来越高的对地观测需求。与常规直线轨迹SAR相比,圆迹SAR具有以下优势[3]:(1)能够获取目标在各方向的散射特征,有利于提高目标识别和地物分类精度;(2)拓宽波数域有效带宽,理论分辨率达亚波长量级,使低波段高分辨成像成为可能;(3)所形成的圆形合成孔径能够获取目标的3维位置信息,突破了常规直线轨迹SAR只能获取2维斜距图像的局限,能有效减小甚至消除SAR影像固有的迭掩、透视缩短和阴影等现象。依据这些独特优势,圆迹SAR在高精度测绘、灾害评估和精细资源管理等领域具有鲜明的应用潜力,一经提出便受到了广泛的关注。
上世纪90年代至本世纪初,圆迹SAR成像技术的研究主要为成像机理研究,点目标仿真及可控暗室实验验证了圆迹SAR的亚波长量级高分辨能力及真3维成像能力。2004年开始,法国宇航局(ONERA)[4]、瑞典国防研究院(FOI)[5]、德国宇航局(DLR)[6]以及中科院电子所[3, 7]等研究机构相继利用机载试验平台开展了圆迹SAR飞行试验,挖掘圆迹SAR在对地观测中的应用优势。2011年,德宇航与中科院电子所先后分别获得了L波段和P波段的360°全方位高分辨圆迹SAR分布式场景图像。图 1展示了中科院电子所获取的圆迹SAR图像与常规条带SAR图像的比较,图 2为场景中典型目标的细节对比,通过比较可以看到,圆迹SAR图像不仅具有更高的分辨率,还获取了目标的全方位散射信息,并有效抑制阴影,展现了更为丰富和精细的地物信息,如圆形水井和圆柱形高铁底座在常规条带SAR图像中仅显示为一个亮点,而在圆迹SAR图像中能够呈现清晰、完整的轮廓,输电线、建筑物与地面构成的二面角等散射方向性较强的目标在常规条带SAR的小角度观测几何下可能观测不到,而圆迹SAR的全方位观测几何总能获取其信息。

|
图 1 2011年8月中科院电子所获取了P波段360°全方位高分辨圆迹SAR图像 Fig.1 P band 360° full-aspect high resolution CSAR image obtained by IECAS on Aug. 2011 |

|
图 2 圆迹SAR图像与常规条带SAR图像的细节对比(HH) Fig.2 Detailed comparison between CSAR images and stripmap SAR images (HH) |
机载圆迹SAR实验展现了圆迹SAR全方位观测带来的显著优势,但其局限性在于,由于天线相对目标视角变化较大(例如,入射角为45°时,视角变化达到90°),多数目标的散射特性不能在整个孔径中保持恒定,限制了其在高程向的分辨能力,难以获得整个场景区的3维分辨图像。
2.2 地球同步轨道SAR简介1978年,K. Tomiyasu首次提出了地球同步轨道SAR(Geosynchronous SAR,GeoSAR)的概念[8],随后初步设计了轨道倾角为50°的GeoSAR系统[9],该系统可将美国本土全境观测时间缩短为3 h,观测周期缩短为1 d。受当时天线工艺、发射功率和运载能力等技术因素限制,GeoSAR在很长一段时间仅停留在概念研究阶段。
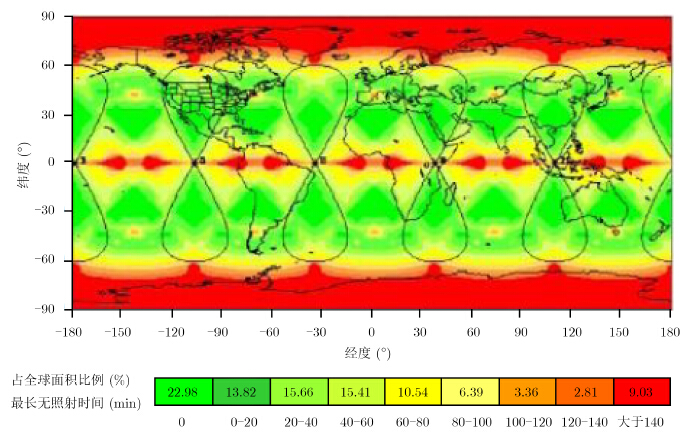
直到2003年,为了构建全球地震活动的监测和预警系统,喷气推进实验室(JPL)在NASA的支持下提出了全球地震卫星系统(Global Earthquake Satellite System,GESS)计划[10, 11],开展了初步的方案和可行性研究,计划发射10颗L波段地球同步轨道星载SAR形成全球不间断覆盖能力。如图 3所示,以60°轨道倾角、5组(每组包含两颗相差180°的卫星)在经度方向上均匀分布的GeoSAR组网卫星为例,其观测能力为:地球表面的瞬时覆盖范围约为80%;约20%地球表面能够实现不间断观测;另约50%地球表面的观测间隙不超过1 h;另约30%地球表面(两极及赤道的部分地区)的观测间隙不超过5个小时;对于大部分地区,在快速响应模式下,能够在10 min内获得20 m分辨率的图像。由此证明,与低轨SAR相比,GeoSAR在地面瞬时覆盖能力和连续观测能力方面具有显著的优势。
|
图 3 美国GESS计划的GEOSAR 组网卫星观测能力 Fig.3 The imaging capability of the American GESS GEOCSAR constellation |
目前,国内外关于GeoSAR的研究主要是针对大倾角圆形轨道形成的“8”字卫星轨迹开展的[9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22],且多研究“8”字形轨迹近似直线部分的2维成像模式。国内多个高校和研究机构都较早开展了GeoSAR研究,主要工作包括:GeoSAR的概念研究[12, 13],GeoSAR双站模式研究[14, 15],GeoSAR的成像机理、信号特征和成像算法研究[16, 17, 18, 19, 20, 21, 22],相关的研究工作还在持续进行中。
3 地球同步轨道圆迹SAR的概念地球同步轨道通过参数设计,还能形成近圆的卫星相对地球轨迹,为圆迹SAR模式提供稳定平台,使SAR载荷的凝视成像模式成为可能。本节将重点讨论地球同步轨道CSAR的轨道生成和分辨率理论。
3.1 轨道生成在无摄运动假设条件下,即轨道仅受到球形对称地球的引力影响,卫星轨道可以是一条椭圆,一条抛物线或一条双曲线,地球位于其两个焦点之间,我们仅对椭圆轨道感兴趣。通常用经典的6根轨描述椭圆的属性,包括:半长轴a;偏心率e;倾角i;升交点W(表示轨道自南向北与赤道面的交点);近地点幅角w(表示升交点到近地点的夹角);真近点角u(随时间变化,表示卫星在椭圆中的当前位置,即距近地点的角度)。
在地心惯性坐标系下,以卫星到地心距离r、经度λ及纬度j来表示卫星的位置,其关于轨道参数的表达式为[23]:
| $\begin{array}{l} {J_s} = 2\left( {\hat n \times {H^i}} \right);{H_s} = 0\\ {J_s} = 0 \end{array}$ | (1) |
卫星轨道周期仅由轨道半长轴决定,地球同步轨道的轨道周期与地球自转周期一致,则地球同步轨道的半长轴均为:
| $A = \sqrt[3]{{\mu /{\psi ^2}}} = 42164.2{\rm{km}}$ | (2) |
“8”字型卫星轨迹是通过大倾角圆形同步轨道形成的,Geo-CSAR的轨迹生成机理则很不同,是在地球静止轨道(地球静止轨道同时满足a=A和i=e=0)的基础上,通过设计较小的偏心率和倾角来实现近似圆形的卫星轨迹。设轨道半径误差为δa=a-A,则当i,e和δa都较小时,式(1)可近似表达为[23]:
| $\left. {\begin{array}{*{20}{l}} {r \approx A + \delta a - Ae\cos \upsilon }\\ {\lambda \approx {\lambda _{\rm{0}}} - 1.5 \cdot (\delta a/A) \cdot \psi t + 2e\sin \upsilon }\\ {\varphi \approx i\sin (\omega + \upsilon )} \end{array}} \right\}$ | (3) |
| ${\lambda _{\rm{0}}}{\rm{ = }}\Omega - G + \arg \left[{\cos \omega + {\rm{j}}\sin \omega \cdot \cos i} \right]$ | (4) |
由式(3)可知,影响地球同步轨道卫星轨迹的主要因素有:(1)由卫星轨道倾角引起纬度方向的简谐振动;(2)由卫星轨道偏心率引起经度方向的简谐振动;(3)由卫星轨道半径误差引起经度上的线性漂移。
考虑到轨道的可重复性,应尽量减小轨道半径误差,不考虑轨道半径误差,满足以下条件时可形成闭合的圆形星下点轨迹:
| $\left. {\begin{array}{*{20}{l}} {\delta a = 0}\\ {\omega {\rm{ = }}\pi {\rm{/2}}{\rm{3}}\pi {\rm{/2}}}\\ {i = 2e} \end{array}} \right\}$ | (5) |
将式(5)代入式(3)可得,GEO-CSAR的卫星轨迹为:
| $\left. {\begin{array}{*{20}{l}} {r \approx A - Ae\cos \upsilon }\\ {\lambda \approx {\lambda _{\rm{0}}} + 2e\sin \upsilon }\\ {\varphi \approx i\cos \upsilon {\rm{ - }}i\cos \upsilon } \end{array}} \right\} $ | (6) |
图 4给出了地心惯性直角坐标系下,满足以下条件:a=A,i=2e,ω=π/2, Ω=G,不同轨道倾角i的Geo-CSAR卫星轨迹。从图中可以看到,卫星轨迹位于赤道上方,在空间中近似为斜椭圆,且关于经线λ0对称,星下点轨迹近似为圆,随着轨道倾角的增大,轨迹半径不断增大。
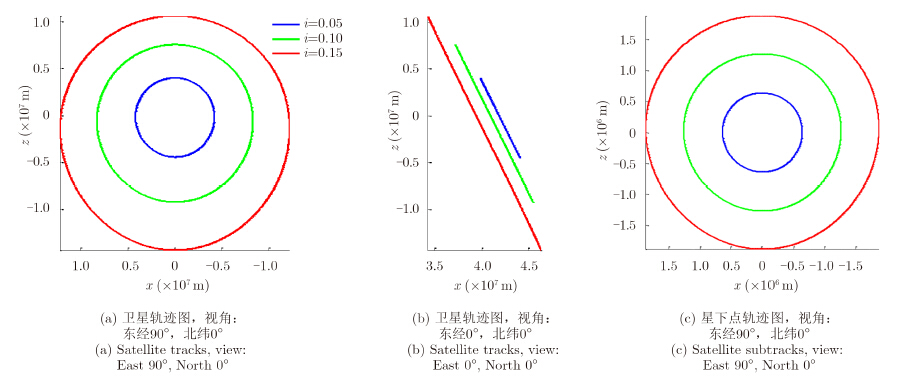 | 图 4 不同轨道参数下的Geo-CSAR卫星轨迹Fig. 4 Geo-CSAR satellite tracks with different orbit parameters |
Geo-CSAR可实现2维和3维两种成像模式:2维成像模式下,全孔径划分为若干弯曲度可忽略的小角度孔径,小角度孔径近似为直线,合成后可获得可视范围内目标区域的2维图像,也可进一步形成同一目标区域的时间序列2维图像,实现对热点区域的动态监视;3维成像模式下,24 h全孔径合成,因天线相对地面目标的观测视角变化较小(约为2i,通常不超过30°),可以认为目标的散射特性在整个孔径内保持恒定,能够获得可视范围内目标区域的高分辨3维图像,实现重点区域的精细观测。本小节将讨论Geo-CSAR的2维和3维分辨率理论。
3.2.1 2维分辨率首先,回顾经典的SAR 2维成像在斜距面的分辨率,斜距向分辨率由发射信号带宽决定,其表达式为:
| ${\rho _{\rm{r}}} = \frac{{\rm{c}}}{{2B}}$ | (7) |
| ${\rho _{\rm{a}}} = \frac{{{\lambda _{\rm{c}}}}}{{4\sin \dfrac{{{\theta _{{\rm{syn}}}}}}{2}}}$ | (8) |
我们更关心的指标是地平面分辨率,该指标能更准确地反映SAR系统对地面目标的分辨能力。与低轨星载SAR相比,Geo-CSAR的成像几何更为复杂,地平面分辨率的计算需要考虑Geo-CSAR成像孔径相对于观测目标的实时几何关系。图 5给出了成像孔径与地面目标之间的几何关系,其中,角度 β表示斜平面与地平面的夹角,角度α表示有效孔径与斜平面-地平面交线之间的夹角。
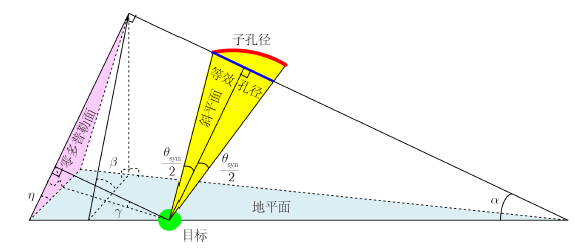 | 图 5 小角度孔径成像几何Fig. 5 Small angle aperture imaging geometry |
地距分辨率的表达式为:
| ${\rho _{{\rm{rg}}}} = \frac{{{\rho _{\rm{r}}}}}{{\cos \eta }}$ | (9) |
| $\cos \eta = \frac{{\cos \beta }}{{\sqrt {{{\sin }^2}\alpha {{\cos }^2}\beta + {{\cos }^2}\alpha } }}$ | (10) |
地平面方位分辨率表达式为:
| ${\rho _{{\rm{ag}}}} = \frac{{{\rho _{\rm{a}}}}}{{\cos \gamma }}$ | (11) |
| $\cos \gamma = \frac{1}{{\sqrt {1 + {{\tan }^2}\alpha {{\tan }^2}\eta } }}$ | (12) |
不同于小角度孔径的斜平面2维成像,360°圆形观测几何下,由于观测斜平面不断变化,能够对观测场景进行3维分辨成像,即获得观测场景散射中心在3维空间中的分布。
图 6给出了地心惯性直角坐标系下全孔径与地面目标之间的几何关系,通过此几何关系可计算得到点目标波数域频谱的支撑域,为分辨率的计算服务。x,y,z 3个方向的波数kx,ky,kz的表达式可通过驻定相位原理得到[24, 25],分别为:
| $\left. {\begin{array}{*{20}{l}} {{k_x} = \frac{{\partial \Phi }}{{\partial {x_{\rm{a}}}}} = - k\frac{{{x_{\rm{a}}} - {x_{\rm{p}}}}}{{{R_{\rm{p}}}}}}\\ {{k_y} = \frac{{\partial {\rm{ }}\Phi }}{{\partial {y_{\rm{a}}}}} = - k\frac{{{y_{\rm{a}}} - {y_{\rm{p}}}}}{{{R_{\rm{p}}}}}}\\ {{k_z} = \frac{{\partial {\rm{ }}\Phi }}{{\partial {z_{\rm{a}}}}} = - k\frac{{{z_{\rm{a}}} - {z_{\rm{p}}}}}{{{R_{\rm{p}}}}}} \end{array}} \right\}$ | (13) |
| $phi = - k{R_{\rm{p}}} = - k\sqrt {{{({x_{\rm{a}}} - {x_{\rm{p}}})}^2} + {{({y_{\rm{a}}} - {y_{\rm{p}}})}^2} + {{({z_{\rm{a}}} - {z_{\rm{p}}})}^2}}$ | (14) |
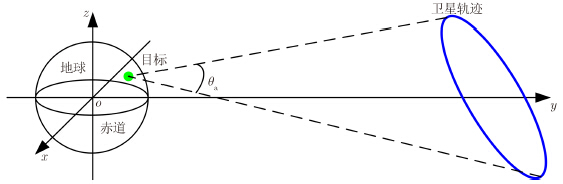 | 图 6 全孔径成像几何Fig. 6 Full aperture imaging geometry |
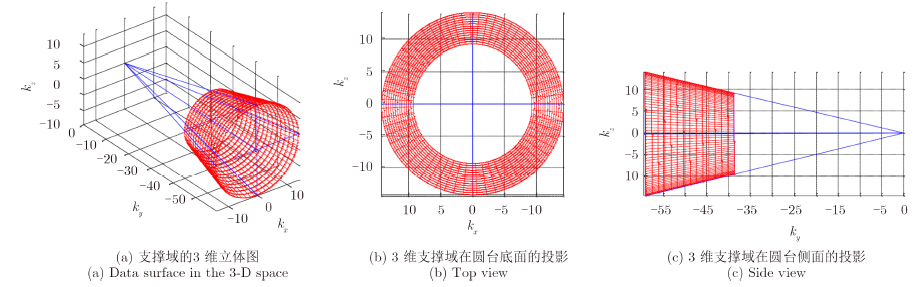 | 图 7 点目标3维频谱支撑域Fig. 7 Data surface observed in the 3-D frequency space |
3维频谱在圆台底面的投影近似为一个中空的圆环,圆环外径为:
| ${B_{\rm{a}}} = {k_{\max }}\sin {\theta _{\rm{a}}}$ | (15) |
| ${\theta _{\rm{a}}} \approx 2i$ | (16) |
| ${\rho _{\rm{a}}} \approx \frac{{{\rm{2}}\pi }}{{{B_{\rm{a}}}}} = \frac{{{\lambda _{\min }}}}{{4\sin ({\theta _{\rm{a}}}/2)}} \approx \frac{{{\lambda _{\min }}}}{{{\rm{4}}\sin i}}$ | (17) |
将与圆台底面垂直的方向定义为高程向,高程向的信号带宽由发射信号带宽和角度θa共同决定,为:
| ${B_{\rm{h}}} = \frac{{4\pi B}}{{\rm{c}}}\cos ({\theta _{\rm{a}}}/2) \approx \frac{{4\pi B}}{{\rm{c}}}\cos i$ | (18) |
| ${\rho _{\rm{h}}} = \frac{{2\pi }}{{{B_{\rm{h}}}}} = \frac{{\rm{c}}}{{2B\cos ({\theta _{\rm{a}}}/2)}} \approx \frac{{\rm{c}}}{{2B\cos i}}$ | (19) |
本节将以典型参数为例,通过仿真研究分析Geo-CSAR的成像能力,轨道参数和系统参数如表 1所示。根据表 1的轨道参数,通过数值仿真得到如图 8所示的卫星轨迹图,蓝色圆环为卫星轨迹,地球上的绿色圆环为星下点轨迹,卫星轨迹半径约为8400 km,略大于地球半径(地球半径约为6400 km)。
| 表 1 轨道参数和系统参数 Tab. 1 Orbital parameters and system parameters |
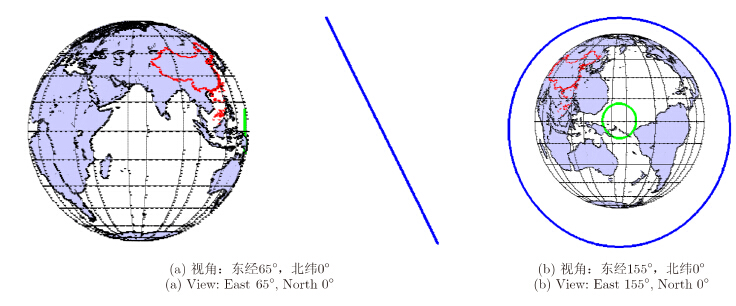 | 图 8 卫星轨迹Fig. 8 Satellite track |
本参数下,天线波束指向只需具有±9.7°的快速切换能力,就可满足可视范围内任意区域的快速响应。此外,波束宽度只需达到2.5°,波束主瓣覆盖区域面积即可达到300万平方公里,相当于1/3的中国疆域,这些特点使Geo-CSAR与现有低轨星载SAR相比,在广域动态监视方面有无法比拟的优势。
下面将更深入地讨论Geo-CSAR的成像能力。
4.1 单颗卫星的成像能力(1) 2维成像能力
首先讨论2维成像模式的分辨率和时间覆盖度(一天内目标区域处于卫星视区范围内的时间称为时间覆盖度)。
根据式(7),本参数下,斜距分辨率为3 m。
以30 min为合成孔径时间,合成孔径角θsyn约为:
| ${\theta _{{\rm{syn}}}} \approx 2{\rm{arcsin}}\left[ {\frac{{A\sin i\sin (2\pi /48/2)}}{{A - {R_{\rm{e}}}}}} \right] = 1.75^\circ {\rm{ }}$ | (20) |
本文以30 min合成孔径时间内,地平面分辨率达到7 m×7 m为2维成像模式的指标。图 9给出了满足该指标要求的地球表面时间覆盖度及星下点轨迹图,其中黄色圆环为星下点轨迹,红色箭头示意了近地点时刻的星下点位置及运动方向。在满足指标的条件下,单颗星的观测能力为:地球表面的瞬时覆盖范围最低时约为15%,最高时约为24%;约23%的地球表面时间覆盖度超过12 h,另约20%的地球表面时间覆盖度超过6 h。星下点附近区域,由于波束入射角较小,地平面分辨率恶化,则满足成像指标要求的时间覆盖度较短。
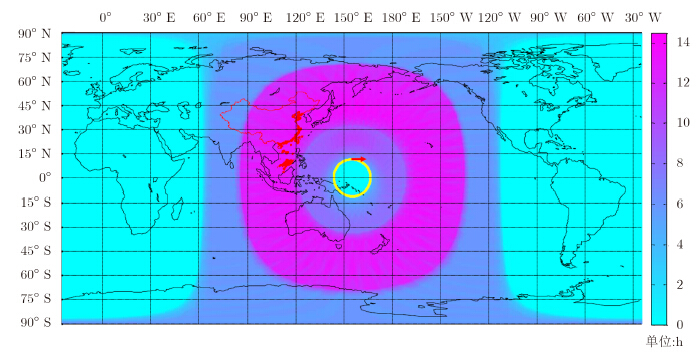 | 图 9 单颗卫星时,达到2维成像指标要求的地球表面时间覆盖度Fig. 9 The time coverage of the land surface in view for a single satellite with the given 2-D imaging performance requirements |
为更直观地展示单颗Geo-CSAR的2维成像能力,下面以位于东经110°,北纬19°(海南)处的点目标为例,给出其在不同时间序列图像中的点扩展函数。在24 h访问周期内形成的48幅时间序列图像中,满足分辨率指标要求的时间序列编号为7~21和36~47,图 10展示了该目标在第10,15,20,36,41,46这6个子孔径中的地平面点扩展函数,可以看到,点扩展函数随着观测几何的变化而变化。
 |
图 10 Geo-CSAR 2维成像模式下,位于东经110°,北纬19°(海南)的点目标的点扩展函数 (从左至右分别为第10,15,20,36,41和46幅序列图像)Fig. 10 The spread function of the point target located at East 110°,North 19° (Hainan) of the Geo-CSAR 2-D imaging mode. (The sequences are 10,15,20,36,41,46 respectively) |
(2) 3维成像能力
3维成像模式下,24 h全孔径合成,全孔径相对于地面目标的视角变化约为2i,本参数下,视角变化约为23°,可以认为目标的散射特性在整个孔径内保持恒定,具备真3维成像的条件。因全孔径相对于地面不同位置处的目标视角变化范围差别不大,则3维分辨率的空变性也不大,根据式(17)和式(19)计算得到:平面分辨率约为0.33 m,高程分辨率约为0.3 m,本文以此作为3维成像模式的指标。图 11给出了满足指标要求的覆盖区域(紫色),覆盖率为地球总面积的33%。
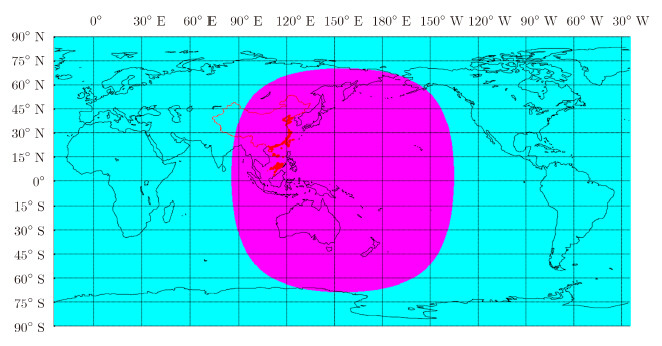 | 图 11 单颗卫星时,3维成像覆盖区域Fig. 11 The 3-D imaging land surface coverage for a single satellite |
为更直观地展示单颗Geo-CSAR的3维成像能力,下面以位于东经110°,北纬19°(海南)处的点目标和东经155°,纬度0°(星下点圆心)处的点目标为例,给出它们360°全孔径合成的3维点扩展函数。
如图 12所示,3维点扩展函数在平面上为贝塞尔函数,在高程向上为sinc函数,且点扩展函数的朝向随着目标位置的变化而变化,但分辨率的空变性不大,24 h覆盖区域都能满足3维分辨率指标要求。
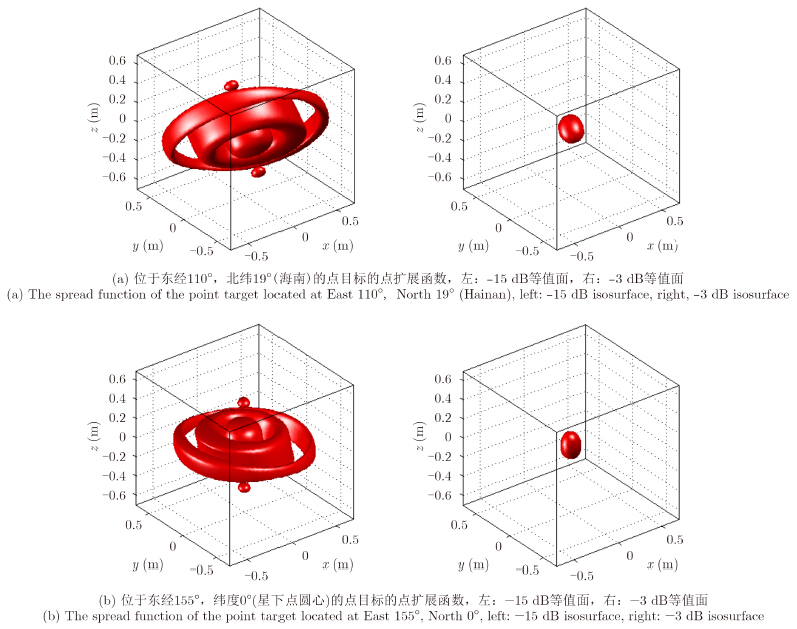 | 图 12 Geo-CSAR 3维成像模式下的点扩展函数Fig. 12 The point target spread function of the Geo-CSAR 3-D imaging mode |
利用多颗星协同工作,可有效提高满足成像指标要求的时间覆盖度。在本例中,采用4组(每组包含两颗相差90°的卫星)均匀地分布于径度方向的卫星网络。图 13给出了4组卫星的星下点轨迹,以黄色线条表示,近地点时刻的星下点位置及运动方向则以红色箭头标示。
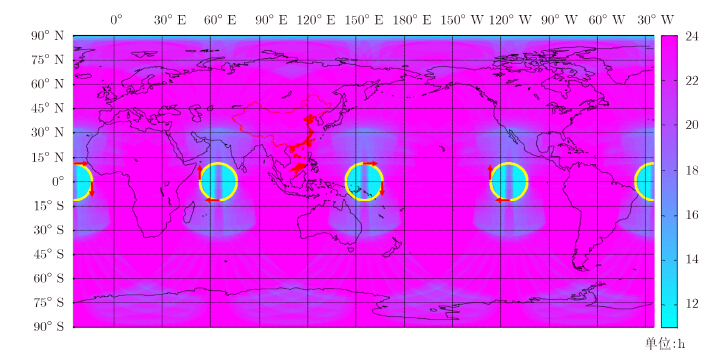 | 图 13 8颗卫星协同工作时,达到指标要求的地球表面时间覆盖度Fig. 13 The time coverage of the land surface in view for a constellation of 8 satellites with the given imaging performance requirments |
图 13还给出了满足2维成像指标要求的地球表面时间覆盖度,其观测能力为:地球表面的瞬时覆盖范围超过86%,最高时可达96%;约35%的地球表面能够实现不间断观测;另约28%的地球表面观测间隙不超过1 h;另约29%的地球表面的观测间隙不超过5个小时;另约8%的地球表面(两极和星下点部分区域)的观测间隙不超过12 h。
3维成像模式下,可在每组卫星中任选1颗,共4颗,对4颗卫星的24 h可视范围进行叠加,得到如图 14所示的3维成像覆盖区域(紫色),覆盖率达到地球表面总面积的92%,非覆盖区(青色)处于两极。
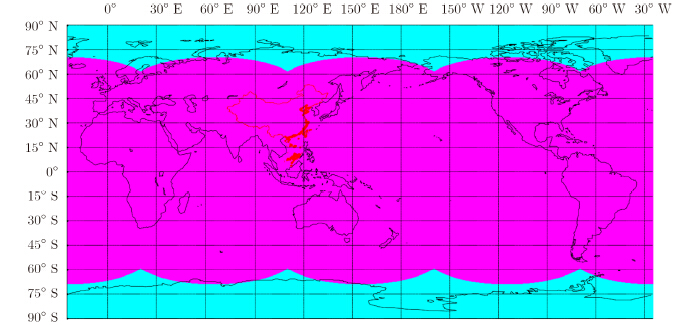 | 图 14 3维成像覆盖区域(紫色区域)Fig. 14 3-D imaging land surface coverage (Purple area) |
本文设计的组网卫星除了能有效提高满足成像指标要求的时间覆盖度,还将单颗星的24 h重访周期缩短为交替的6 h和18 h,更有利于重轨形变监测等应用,能更及时地监测地球表面的细微变化,为地震预测、灾害评估等应用提供重要数据。
5 结束语地球同步轨道通过轨道参数设计可在距地36000 km高空形成近圆的卫星相对地球轨迹,为圆迹SAR提供了一个稳定平台。Geo-CSAR兼备了GeoSAR和CSAR各自的优势,首先,由于轨道高度较高,Geo-CSAR在重复观测周期、测绘带宽和可视能力等方面的性能是低轨SAR无法比拟的,此外,与“8”字形卫星轨迹相比,Geo-CSAR的圆形
卫星轨迹不仅能更好地对可视范围内重点区域进行定点连续观测,获取较高分辨率的2维时间序列图像,实现热点区域的动态监测,更重要的是,还具有特有的3维成像能力,通过回波数据的360°相干累积,能够获取观测场景的高分辨3维图像,实现目标的精确3维定位。因此,Geo-CSAR是实现全球连续观测的有效途径之一,尤其在全球性的大面积区域动态连续监视、高分辨率3维测绘、形变监测等领域具有广阔的应用前景。
Geo-CSAR的实现目前还面临着理论和技术上的挑战,除了系统代价高、受电离层影响大等GeoSAR的共性问题外,Geo-CSAR的研究难点主要包括以下两个方面:(1)Geo-CSAR的合成孔径时间较长(3维成像时达到24 h),对轨道测量手段的稳定性和精度都提出了极高的要求。因此,长合成孔径时间条件下Geo-CSAR的高精度定轨和运动补偿问题有待研究和突破。(2)Geo-CSAR成像区域面积大、合成孔径时间长、分辨率高,将不仅产生海量数据问题,还使地球的球面性以及卫星轨迹的非规则性等因素变得不可忽视,这给成像处理,尤其是3维成像处理,带来了巨大挑战,亟需开展Geo-CSAR的高精度大区域快速成像算法研究。
随着相关研究的不断地深入[26, 27, 28, 29],以及星载SAR成像技术领域的不断发展,Geo-CSAR有望在不久的未来成为现实,成为全球不间断覆盖的一个有效手段。
| [1] | Battagliere M L. The COSMO-SkyMed experience overview[OL]. https://wiki.services.eoportal.org/.../COSMOSkyMed_ Experience_WORKSHOP_ESRIN_Oct_2012_ FinalVersion.ppt.( 1) 1) |
| [2] | Zhu X and Bamler R. Very High resolution spaceborne SAR tomography in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4296-4308.( 1) 1) |
| [3] | 洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135. Hong Wen. Progress in circular SAR imaging technique[J]. Journal of Radars, 2012, 1(2): 124-135.( 2) 2) |
| [4] | Palm S,Oriot H M,and Cantalloube H M. Radargrammetric DEM extraction over urban area using circular SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(11): 4720-4725.( 1) 1) |
| [5] | Frölind P O, Gustavsson A, Lundberg M, et al.. Circularaperture VHF-band synthetic aperture radar for detection of vehicles in forest concealment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(4): 1329-1339.( 1) 1) |
| [6] | Ponce O, Prats P, Marc R C, et al.. Processing of circular SAR trajectories with fast factorized back-projection[C]. International Geoscience and Remote Sensing Symposium, Vancouver, 2011: 3692-3695.( 1) 1) |
| [7] | Lin Y, Hong W, Tan W, et al.. Airborne circular SAR imaging: results at P-band[C]. International Geoscience and Remote Sensing Symposium, Munich, 2012: 5594-5597.( 1) 1) |
| [8] | Tomiyasu K. Synthetic aperture radar in geosynchronous orbit[C]. Antennas and Propagation Symposium, Maryland, 1978: 42-45.( 1) 1) |
| [9] | Tomiyasu K and Pacelli J L. Synthetic aperture radar imaging from an inclined geosynchronous orbit[J]. IEEE Transactions on Geoscience and Remote Sensing, 1983, 21(3): 324-329.( 2) 2) |
| [10] | NASA, JPL. Global earthquake satellite system: a 20-year plan to enable earthquake prediction[OL]. http://solidearth. jpl.nasa.gov/GESS/3123_GESS_Rep_2003.pdf, 2003.( 2) 2) |
| [11] | Madsen S N, Edelstein W, Didomenico L D, et al.. A geosynchronous synthetic aperture radar: for tectonic mapping, disaster management and measurements of vegetation and soil moisture[C]. International Geoscience and Remote Sensing Symposium, Sydney, 2001: 447-449.( 2) 2) |
| [12] | 朱敏慧. 地球同步轨道星载合成孔径雷达概念研究[J]. 现代雷 达, 2011, 33(5): 1-4. Zhu Min-hui. A study on the concept of geosynchronous synthetic aperture radar[J]. Modern Radar, 2011, 33(5): 1-4.( 2) 2) |
| [13] | 毛二可, 曾涛, 胡程, 等. 基于地球同步轨道合成孔径雷达的双 基地探测系统: 概念及潜力[J]. 信号处理, 2013, 29(3): 285-292. Mao Er-ke, Zeng Tao, Hu Cheng, et al.. Bistatic detection based on geosynchronous SAR: concept and potentiality[J]. Journal of Signal Processing, 2013, 29(3): 285-292.( 2) 2) |
| [14] | 孔德亮. 基于大面积定点区域连续观测的雷达新概念新技术研 究[D]. [Ph.D. dissertation], 中国科学院电子学研究所, 2006: 1-33. Kong De-liang. New radar architecture and technology based on incessant fixed region observation[D]. [Ph.D. dissertation], Institute of Electronics of Chinese Academy of Sciences, 2006: 1-33.( 2) 2) |
| [15] | 袁媛, 袁昊, 雷玲, 等. 一种同步轨道星机双基SAR 成像方 法[J]. 雷达科学与技术, 2007, 5(2): 128-132. Yuan Yuan, Yuan Hao, Lei Ling, et al.. An imaging method of GEO spaceborne-airborne bistatic SAR[J]. Radar Science and Technology, 2007, 5(2): 128-132.( 2) 2) |
| [16] | 黄丽佳. 中高轨道 S A R 成像算法研究[D]. [P h. D. dissertation], 中国科学院电子学研究所, 2011: 1-12. Huang Li-jia. Imaging algorithm for medium-earth-orbit SAR[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2011: 1-12.( 2) 2) |
| [17] | 郑经波. 地球同步轨道合成孔径雷达系统分析及工作模式研 究[D]. [Ph.D. dissertation], 中国科学院电子学研究所, 2011: 1-9. Zheng Jing-bo. Study on system analysis and working modes for geosynchronous earth orbit synthetic aperture radar[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2011: 1-9.( 2) 2) |
| [18] | Long T, Dong X, Hu C, et al.. A new method of zero-Doppler centroid control in GEO SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(3): 511-515.( 2) 2) |
| [19] | Hu C, Liu Z, and Long T. An improved CS algorithm based on the curved trajectory in geosynchronous SAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(3): 795-808.( 2) 2) |
| [20] | 史洪印, 周荫清, 陈杰. 同步轨道星机双基地3通道SAR 地面 运动目标指示算法[J]. 电子与信息学报, 2 0 0 9, 3 1 ( 8 ) : 1881-1885. Shi Hong-yin, Zhou Yin-qing, and Chen Jie. An algorithm of GEO spaceborne-Airborne bistatic three-Channel SAR ground moving target indication[J]. Journal of Electronics & Information Technology, 2009, 31(8): 1881-1885.( 2) 2) |
| [21] | 李军, 邢孟道, 李亚超, 等. 同步轨道SAR 参数分析及成像方 法[J]. 系统工程与电子技术, 2010, 32(5): 931-936. Li Jun, Xing Meng-dao, Li Ya-chao, et al.. Parametric analysis and imaging method of geosynchronous SAR[J]. Systems Engineering and Electronics, 2010, 32(5): 931-936.( 2) 2) |
| [22] | Bao M, Xing M, and Li Y C. Chirp scaling algorithm for GEO SAR based on fourth-order range equation[J]. Electronic Letters, 2012, 48(1): 41-42.( 2) 2) |
| [23] | Soop E M. Handbook of Geostationary Orbits[M]. Sweden, The Netherlands: Eur. Space Agency Sci. Tech, 1994: 3-34.( 2) 2) |
| [24] | 林赟. 圆迹合成孔径雷达成像算法研究[D]. [P h. D. dissertation], 中国科学院电子学研究所, 2011: 1-15. Lin Yun. Study on algorithms for circular Synthetic( 1) 1) |
| [25] | Aperture Radar imaging[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2011: 1-15. Lin Y, Hong W, Tan W, et al.. Extension of range migration algorithm to squint circular SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 651-655.( 1) 1) |
| [26] | 寇蕾蕾. 地球同步轨道圆迹 SAR 干涉机理研究[D]. [Ph.D. dissertation], 中国科学院电子学研究所, 2011: 1-23. Kou Lei-lei. Study on interferometric mechanism of geosynchronous circular SAR[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2011: 1-23.( 1) 1) |
| [27] | Kou L, Wang X, Xiang M, et al. Interferometric estimation of three-dimensional surface deformation using geosynchronous circular SAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1619-1635.( 1) 1) |
| [28] | 刘启. 地球同步轨道圆迹SAR成像方法研究[D]. [Ph.D. dissertation], 中国科学院电子学研究所, 2012: 1-18. Liu Qi. Investigation on the imaging methods for geosynchronous circular SAR[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2012: 1-18.( 1) 1) |
| [29] | Liu Q, Hong W, Tan W, et al.. An improved polar format algorithm with performance analysis for geosynchronous circular SAR 2D imaging[J]. Progress in Electromagnetics Research, 2011, 119: 155-170.( 1) 1) |


