太赫兹频段是指频率从300 GHz到10 THz,介于微波与红外之间的电磁波谱区域。由于这一区域属于传统电磁学与现代量子学的过渡区域,缺乏有效的理论基础,多年来一直是研究的空白领域和国家学术界关注的热点。
近年来,随着太赫兹雷达关键器件的成功研制,其独特的特性逐渐体现出广阔的应用前景与优势。太赫兹频段的波长远小于现有微波、毫米波,更适合于极大信号带宽和极窄天线波束的实现,有利于实现目标的高分辨率探测与成像。太赫兹波对非极性材料具有良好的穿透特性,可以通过非接触方式对隐藏于衣服、包装箱以内的危险品进行检测。
目前,针对太赫兹高分辨率雷达的研究主要集中在系统结构、太赫兹雷达关键器件的研究上,而太赫兹频段的杂波特性作为太赫兹高分辨率雷达检测中不可或缺的一部分却迟迟未得到有效的理论分析与实验验证。本文针对太赫兹高分辨率雷达对地探测的需求,对传统杂波的统计模型及参数估计方法进行了分析,并使用实测数据对太赫兹高分辨率雷达的杂波统计模型进行了估计与验证。
本文安排如下,第2节对传统杂波概率统计模型及参数估计方法进行了整合分析;第3节介绍了太赫兹高分辨率雷达与杂波测量实验的设计;第4节利用Weibull分布、Gamma分布、G0分布以及K分布对实测数据进行了拟合,并分别检验了模型对实测杂波数据的拟合效果,结论显示G0分布模型对太赫兹频段的杂波统计特性拟合度最优。
2 杂波概率统计模型及参数估计方法根据实测杂波数据确定杂波的分布类型属于拟合优度检验问题。首先采用某种杂波概率统计模型对实测数据进行参数估计,之后使用假设检验的方法确定对实测数据描述最准确的概率统计模型。本文主要采用以下几种概率统计模型对实测数据进行参数估计。
Weibull分布由瑞典物理学家Wallodi Weibull于1939年引进,是可靠性分析及寿命检验的理论基础,对雷达杂波数据的统计描述也具有一定的有效性。其概率密度函数为:
| $f\left( {z/\eta ,\mu } \right) = \frac{\eta }{{{\mu ^\eta }}}{z^{\eta - 1}}\exp \left[{ - {{\left( {\frac{z}{\mu }} \right)}^\eta }} \right], z \ge 0$ | (1) |
Weibull分布很好地描述了非瑞利包络数据的统计模型。瑞利分布和负指数分布是Weibull分布取特定参数时的特例,因此不难理解,与瑞利分布相比,Weilbull分布模型能在更宽的条件范围内很好地与实验数据匹配。
1997年Frery等人[3, 4]提出G0模型用于描述混合杂波的统计特性,其概率密度分布函数为:
| $f(x) = \frac{{4{{\left( {\lambda L} \right)}^{\frac{{L + \alpha }}{2}}}}}{{\Gamma \left( L \right)\Gamma \left( \alpha \right)}}{x^{L + \alpha - 1}}{K_{\alpha - L}}\left( {2x\sqrt {\lambda L} } \right)$ | (2) |
其中,L为视数,不同的$\alpha $和λ可以逼近不同的分布描述杂波的统计特性。
Gamma分布是一种简单、基本的概率统计模型。很多统计模型都是在Gamma模型上形成的。其概率密度函数为:
| $f(z,\mu ,L) = \frac{{{L^L}}}{{\mu \Gamma (L)}}{\left( {\frac{z}{\mu }} \right)^{L - 1}}\exp \left( { - \frac{{Lz}}{\mu }} \right)$ | (3) |
K-root分布模型属于乘积噪声模型;是在假设地面RCS起伏服从Gamma分布、相干斑噪声服从单位均值Gamma强度分布的条件下推导得到的SAR图像概率统计模型。
K-root分布的概率密度函数:
| $\begin{array}{l} f(z/L,M,\mu ) = \frac{4}{{\Gamma (L)\Gamma (M)}}{\left( {\frac{{LM}}{\mu }} \right)^{\frac{{(L + M)}}{2}}}\\ \qquad \qquad \qquad \times {z^{(L + M - 1)}}{K_{M - L}}\left( {2z{{\left( {\frac{{LM}}{\mu }} \right)}^{\frac{1}{2}}}} \right),z \ge 0 \end{array}$ | (4) |
由于Gamma分布能够描述高分辨率条件下不均匀地物杂波特性,因而由此推导得到的K-root分布对于不均匀地物一般都具有较好的拟合效果。
对于上述各类分布,本文使用对数累积(MoLC)方法对其进行参数估计,这种方法在分析随机变量时使用Mellin变换代替傅里叶变换。表 1中列举了几种常用的分布模型及其MoLC方程,对于对数正态分布、Nakagami分布、广义高斯瑞利分布、对称α稳态分布的概率密度函数及其模型在这里就不再冗述。
| 表 1 各类分布模型MoLC参数估计方法 Tab. 1 MoLC parameters estimation of distributionmodels |
本文使用基于双频率源驱动结构的300 G Hz太赫兹雷达对场景杂波进行测量。系统简易结构框图如图 1所示。扫频源采用DDS+PLL结构产生1.8~2.1G Hz的线性扫频输出信号,与发射链路的7.5 G Hz点频源混频后,输出至发射端倍频链路,经过36次倍频后,产生335~345G Hz的发射信号。接收天线接收回波信号,与2次谐波混频器信号进行混频,产生中心频率为900MHz的中频信号,其中,混频器信号由扫频源与7.48G Hz点频源混频并经过18次倍频产生。中心频率为900 MHz的中频信号与900 MHz本振信号混频后产生I/Q两路信号。为适应在任意距离范围内进行探测,系统在对回波信号进行数字采样之后,采用数控振荡器(NCO)产生目标距离对应频率的本振信号分别与I/Q两路信号进行混频,经低通滤波器后,得到目标场景处的回波信号。系统发射信号中心频率为340G Hz,带宽为10G Hz,理论分辨率为1.5 cm,脉冲时间宽度为300 ms,系统调频斜率为3.36×1013 HZ/s,系统采样后低通滤波器带宽为600 kHz,对应回波场景大小为2.68 m。
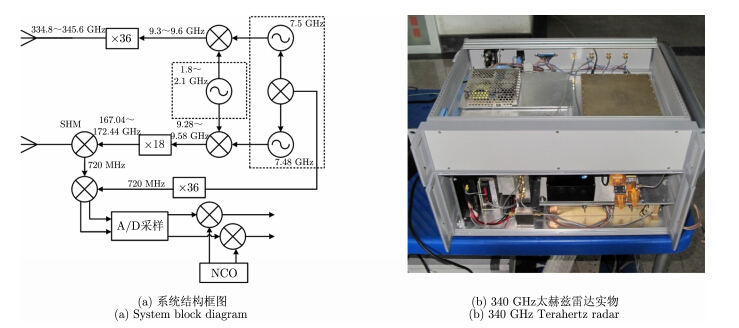 | 图 1 太赫兹高分辨率雷达系统Fig. 1 Terahertz high-resolution radar system |
针对太赫兹雷达对地探测应用场景,实验设置如图 2所示,雷达天线高度h,俯仰角∅与天线波束宽度θ已知,由此,可以计算出照射场景直径d,从而得到地面回波中最小距离信号与最大距离信号对应的频率为:
| $\left. \begin{array}{l} {f_{\min }} = \frac{{2k{R_{\min }}}}{{\rm{c}}}\\ {f_{\max }} = \frac{{2k{R_{\max }}}}{{\rm{c}}} \end{array} \right\}$ | (5) |
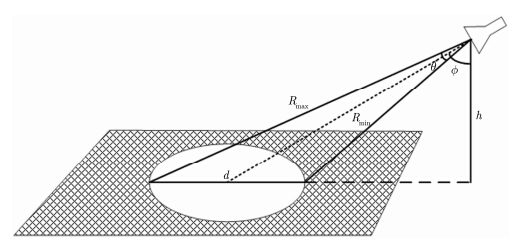 | 图 2 实验场景设计Fig. 2 Design specification of experiment |
由于系统采用超外差接收的方式采集回波,所以对时域数据进行傅里叶变换处理可得到如图 3所示的脉冲频谱,其中图 3(a)为单次回波脉冲频谱,图 3(b)为多次回波脉冲频谱。实验中,波束照射范围内除地面以外未放置其他目标,故回波信号中仅包含目标场景地面的回波,其中,所照射的地面为室内常用的瓷砖,被照射表面较为均匀,无明显的褶皱。
 | 图 3 实测数据频谱Fig. 3 Spectrum of measured data |
利用第2节中对杂波特性的参数估计方法,本文分别对Weibull分布、Gamma分布、G0分布和K分布进行了参数估计和模型拟合。结果如图 4所示,从模型拟合曲线可以看到,G0分布与K分布对实测数据的拟合度较高,Weibull分布与Gamma分布的拟合效果较差。
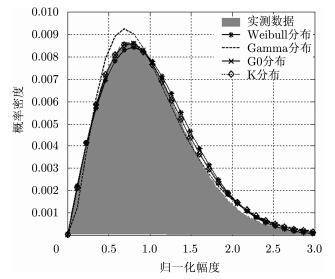 | 图 4 不同分布模型对实测数据拟合结果Fig. 4 Fitted curve of different distribution models |
为了进一步确定太赫兹高分辨率雷达系统的杂波特性,本文采用卡方检验的方法对不同模型进行拟合优度检验。卡方检验法是由英国统计学家皮尔逊于1900年提出的,以其固有的简洁、直观的优点,在分布的拟合优度检验中得到了广泛的应用。首先构造一个统计量如式(6)所示:
| ${\chi ^2} = \sum\limits_{i = 1}^n {\frac{{{{\left( {{f_i} - {F_i}} \right)}^2}}}{{{F_i}}}} $ | (6) |
本文共进行了10次实验,并分别对10次实测数据进行数据拟合,使用卡方检验的方法对上述几种分布的拟合度进行了分析与验证,结果如表 2所示。
| 表 2 实测数据x2检验结果 Tab. 2 Chi-square test results of measured data |
实验测试环境为室内铺设瓷砖的地面,虽然瓷砖表面较为均匀,但是瓷砖间接缝的尺寸远大于实验所使用的太赫兹波长( $\lambda \approx 0.9 \,{\rm{mm}}$),其回波与瓷砖表面相比有很大不同。所以,对太赫兹而言,本次实验测试场景内不仅有较为均匀的瓷砖表面,还有瓷砖接缝等不均匀程度较高的区域,这些不均匀区域杂波的真实后向散射强度分量更为复杂,此时用Gamma分布对其建模会产生较大的偏差,所以表 2中K分布对实测数据的拟合精度不高。
由于G0分布模型具有更强的杂波建模能力,能够精确描述高分辨率雷达回波中的均匀区域、一般均匀区域以及极不均匀区域的杂波特性,对测试环境中较为均匀的瓷砖表面杂波分量与不均匀的瓷砖接缝区域杂波分量拟合能力较强,所以G0分布的拟合效果优于K分布的拟合效果,更接近实际数据直方图。
5 结束语本文对传统杂波的统计概率模型及相应的参数估计方法进行了分析,利用自行研制的340 GHz太赫兹高分辨率雷达进行了杂波测量实验,并通过参数估计、卡方检验等方法分别分析了Weibull分布、Gamma分布、G0分布与K分布对太赫兹频段杂波特性的拟合效果。结论显示,G0分布模型对太赫兹频段室内地面杂波的统计特性拟合度为最优。
| [1] |
Oliver C J.Optimum texture estimators for SAR clutter[J]. Journal of Physics D, Applied Physics, 1993, 26(11): 1824-1835.
( 3) 3)
|
| [2] |
Li H C, Hong W, Wu Y R, et al.. On the empirical-statistical modeling of SAR images with generalized gamma distribution[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(3): 386-397.
( 2) 2)
|
| [3] |
Frery A C,Muller H J, Yanasse C C F, et al.. A model for extremely heterogeneous clutter[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997,35(3): 648-659.
( 3) 3)
|
| [4] |
Cui S and Datcu M. Coarse to fine patches-based multitemporal analysis of very high resolutionsatellite images[C]. Proceeding of 6th International Workshop on the Analysis of Multi-Temporal Remote Sensing Images, Trento, Italy, 2011: 85-88.
( 3) 3)
|
| [5] |
Oliver C J and Quegan S. Understanding Synthetic Aperture Radar Images[M]. Norwood, MA, USA: Artech House, 1998: 128-130.
( 6) 6)
|
| [6] |
Nicolas J M.Introduction to second kind statistics: application of logmoments and log-cumulants to second kind statistics: application of logmoments and log-cumulants to analysis of radar images[J]. Traitement du Signal, 2002,19(3): 139-167.
( 4) 4)
|
| [7] |
Krylov V andZerubia J. Generalized gamma mixtures for supervised SAR image classification[C]. Proceedings of GraphiCon 2010, Saint-Pertersburg, Russia, 2010: 107-110.
( 1) 1)
|
| [8] |
Tadjudin S and Landgrebe D A. Robust parameter estimation for mixture model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(1): 439-445.
( 1) 1)
|
| [9] |
Moser G, Zerubia J, and Serpico S B. SAR amplitude probability density function estimation based on a generalized Gaussian model[J]. IEEE Transactions on Image Processing, 2006, 15(6): 1429-1442.
( 1) 1)
|
| [10] |
Szajnowski W. Estimator of log-normal distribution parameters[J]. IEEE Transactions on Aerospace and Electronic Systems, 1977, AES-13(5): 533-536.
( 1) 1)
|
| [11] |
Stacy E W. Ageneralized of the Gamma distribution[J]. The Annals of Mathematical Statistics, 1962, 33(3): 1187-1192.
( 1) 1)
|


