②(中国空气动力研究与发展中心 绵阳 621000)
②(China Aerodynamics Research and Development Center, Mianyang 621000, China)
合成孔径雷达(Synthetic Aperture Radar,SAR) 作为一种有效的全天时、全天候的遥感手段被广泛地应用于军事和民用领域。目前投入使用的大多数SAR系统沿直线孔径运动,只具备2维成像能力。在实践中,存在很多应用需要利用到目标的3维特征信息,3维信息更有利于雷达目标的自动检测和识别,从而大大减少人工判读的工作量。
实际上,平台沿直线轨迹运行的要求并非合成孔径所必需,平台沿曲线运动形成的合成孔径也是较常见的现象[1, 2]。曲线合成孔径雷达(CurviLinear SAR,CLSAR)正是利用雷达平台在方位-高度平面的曲线运动形成曲线孔径,在高度和方位向同时形成大的合成孔径,从而具有高程分辨能力,克服了干涉SAR存在的高度模糊缺陷,是一种具有实际意义的3维成像系统[3, 4, 5, 6, 7]。CLSAR是一种工作在类似聚束模式下的新型微波对地观测技术,与常规SAR相比,除在孔径上有所差别外对雷达系统无额外要求,因此它可以作为多模态SAR系统平台的一种模式使用[8]。
一种特殊的CLSAR形式是圆迹合成孔径雷达(Circular Synthetic Aperture Radar,CSAR)[4, 9],它以雷达平台环绕场景的 圆周运动获取场景的 全方位观测信息,从而实现超高分辨率成像,并且具备一定的3维成像能力。相对于CLSAR,CSAR对平台的运动提出更严格的要求,而CLSAR则灵活性更强,利用CLSAR进行目标3维特征提取也是雷达遥感领域的难点问题。有关CSAR的发展概况在文献[4]中已有详尽描述,本文将重点关注一般形式CLSAR 3维成像的发展状况。
一方面,设计有效的特征提取算法是进行目标3维特征提取的关键,另一方面,目标特征估计精度决定于雷达参数、观测几何和目标位置等因素,设计能获得最优特征估计精度的曲线孔径也是CLSAR研究的重要方面。由于CLSAR在3维空间的采样不是完整而是稀疏的,采用直接的FFT变换重建的目标图像具有极高旁瓣,不具有实际应用意义[5]。已有的目标重建方法主要是基于谱估计的参数化方法,如CLEAN[5, 6],IMP[7],ML[7],RELAX[3, 7, 10],PML[11, 12]等以及为降低运算量[13, 14, 15, 16, 17]、考虑存在运动误差情况[18, 19, 20, 21]的改进算法。在孔径设计上,文献[22, 23]提出以参数估计的CRB下限为评价指标来指导孔径设计,文献[24]则通过对各种形状孔径的性能进行仿真,得到关于孔径形状的初步结论。
总体上讲,CLSAR自提出发展至今已有10多年,但仍有不少待解决的问题,已有的重构算法存在局部优化等问题,在孔径设计上还缺乏足够的理论分析和研究。本文主要分析现有方法的原理,指出CLSAR研究存在的关键问题,并展望可能的研究方向。本文第2节简略介绍CLSAR研究历程中的重要进展,第3节是CLSAR数据模型简介,第4节综述CLSAR 3维目标特征提取算法和孔径设计方法,第5节展望CLSAR未来进一步研究的可行方向。 2 CLSAR研究进展
1994年,美国海军地面战中心(naval surface warfare center)的Knaell[5]博士首次论证了CLSAR的可行性,提出了成像算法,并通过实验得到了几种孔径形状下最初的重建结果。1997年,佛罗里达大学的Li等人[10]详细推导了全孔径和曲线孔径下的数据模型,提出利用RELAX方法进行目标重构,给出了参数估计的CRLB (Cramer Rao Low Bound)。1999年,Li等人[19]针对存在飞行误差的情况,设计了一种能够同时进行运动补偿和目标特征提取的AUTO-RELAX算法,通过仿真证明在存在运动误差情况下新算法能大幅降低估计误差。2004年,苏志刚等人[13]利用散射点的距离参数和垂直于距离方向上参数之间的弱耦合性将散射点位置估计解耦为顺序估计,仿真表明该算法在降低运算复杂度的同时没有造成性能损失。2005年,苏志刚等人[14]利用前述思想提出了一种非迭代方法,能够进一步降低运算的复杂度。2006年,Liu等人[25]提出了一种方位维条带、高度维聚束的复合模式CLSAR,能够在保持高度分辨率的同时进行大测绘带观测。同年,唐智[24]根据信号模型对几种典型曲线孔径进行了仿真,根据仿真结果提出了关于孔径最优设计的初步结论。苏志刚等人[22]利用参数估计中的CRB下限,推导了不依赖于目标特征的孔径评价指标,为孔径的设计提供了指导。2008年,苏志刚等人[26]将Capon波束形成方法应用到目标重建中,提出了一种非参数自适应方法,该方法能有效压缩目标旁瓣,消除目标遮掩。近年来,张子善[3]、庞守宝[27]等学者也进一步在曲线SAR 3维成像结构、降维RELAX算法等方面提出了自己的见解。 3 CLSAR数据模型
CLSAR成像系统观测几何如图 1所示。被成像区域为地面上由数个点目标组成的3维区域。以被成像区域中心为原点建立坐标系,X,Y,Z轴正方向分别代表斜距方向、方位方向和高度方向。曲线孔径由雷达平台以中心斜距Ro 绕坐标原点运动形成。 表示雷达平台与 处散射点之间的距离,$\left\{ {{\theta _m},{\phi _m}} \right\}_{m = 1}^M$为雷达相对坐标系的视角(方位角和仰角),M为观测视角的数目。在观测角(θm,∅m)下,雷达距离坐标中心Rom,距离散射点Ro。
| $r(n,m) = \sum\limits_{k = 1}^K {{\alpha _k}} \exp \left[{{\rm{j}}\left( {{x_k}{K_x} + {y_k}{K_y} + {z_k}{K_z}} \right)} \right] + e(n,m)$ | (1) |
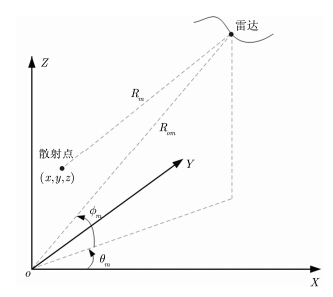 | 图 1 CLSAR工作几何图Fig.1 The geometry of CLSAR |
在曲线孔径情况下,接收信号可以看作对全孔径波数域数据的采样,其中采样矩阵是一个稀疏矩阵,非零元素由曲线形状决定,并对应于曲线孔径上的观测点。全孔径下的3维目标空间重建就是一个简单的3维傅里叶变换,曲线孔径由于是对全孔径的波数域数据乘上一个稀疏的加权因子${\rm{Curv\_Fac}}({K_x},{K_y},{K_z}),$ 3维目标空间重建实际上变成了一个反卷积问题。如果直接对曲线孔径的波数域数据作FFT,则重建的3维空间目标由于叠加了与${\rm{Curv\_Fac}}(x,y,z)$的卷积,旁瓣将大大变强。大的旁瓣将使所成图像的分辨效果受到影响,造成虚假目标的,同时旁瓣造成的光斑使大目标在图像上分裂为多个小的目标。因此,旁瓣的干扰问题在CLSAR的成像过程中显得尤为突出,甚至直接影响到CLSAR所成图像的可用性。为减小这些旁瓣的影响,需要考虑其它方法。
在第m个观测角下,式(1)信号中的每个目标分量可看成1维正弦信号,其频率为:
| ${\omega _k}(m) = {x_k}\cos {\theta _m}\cos {\phi _m} + {y_k}\sin {\theta _m}\cos {\phi _m} + {z_k}\sin {\phi _m}$ | (2) |
则式(1)信号可重新表示为:
| $r(n,m) = \sum\limits_{k = 1}^K {{\alpha _k}} \exp \left\{ {{\rm{j}}{\omega _k}(m){\tau _n}} \right\} + e(n,m)$ | (3) |
因此,在第m个观测角下,式(1)的接收信号可看作是在噪声环境中的多个正弦信号的累加。关于目标的3维特征提取问题转换为参数估计问题,可以利用估计理论进行特征提取和性能分析。 4 CLSAR目标3维特征提取和孔径设计方法 4.1 RELAX算法
RELAX算法适用于对由数个散射点组成的目标的特征提取。RELAX算法通过最小化非线性最小二乘代价函数
| $\begin{array}{l} C\left( {\left\{ {{{\widehat \alpha }_k},{{\widehat x}_k},{{\widehat y}_k},{{\widehat z}_k}} \right\}_{k = 1}^K} \right)\\ = {\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {\left| {r(n,m) - \sum\limits_{k = 1}^K {{\alpha _k}\exp \left\{ {{\rm{j}}{\omega _k}(m){\tau _n}} \right\}} } \right|} } ^2} \end{array}$ | (4) |
RELAX算法存在的运算复杂度高的缺点,特别是3维傅里叶变换的运算量很大,可以考虑利用接收数据的内在性质,降低傅里叶变换的维数。苏志刚等人[13]利用接收数据中散射点的距离参数和垂直距离方向的参数之间的弱耦合性特点,将目标的3维位置估计问题解耦为1维距离参数估计和2维方位及高度参数的估计问题,并顺序地将其估计出来,在获得所有散射点的3维特征后再用迭代的方式对估计值进行求精。仿真结果表明,该算法在基本不损失性能的情况下能有效降低运算复杂度。后续又提出了非迭代的降维RELAX算法[14],它克服了原算法求精过程中在估计出每个散射点特征后需要对其它所有目标进行特征更新的步骤,进一步降低了运算量。
4.3 自聚焦RELAX算法由于存在大气的扰动和平台位置的不确定性等因素,导致雷达相对场景中心的位置不能精确测定,进而严重影响目标特征提取的性能[19],因此,必须估计出运动误差(孔径误差)和相位误差(参考点到雷达距离的不确定性)并将其补偿。自聚焦RELAX算法能够在实现运动补偿的前提下进行目标特征提取。通过初始目标特征来迭代估计出真实的运动轨迹,并进行运动补偿,进而通过RELAX算法实现目标重构。
4.4 非参数化算法以RELAX算法为代表的CLSAR成像算法都是参数化方法,存在着运算复杂度高、对模型误差敏感以及需要已知散射点数目等缺陷。苏志刚等人[26]将谱估计理论中的RCB (RobustCapon Beamforming)方法引进到CLSAR成像中,RCB方法是一种非参数自适应方法,在数据解耦合的基础上,设计中心频率为感兴趣频率的低通滤波器,提取目标位置并估计RCS。该方法能够降低目标间的相互干扰和遮掩效应。
4.5 孔径设计方法孔径最优设计包括孔径形状、孔径尺度和采样数3方面的优化。早期研究主要是通过直观比较一些典型非直线孔径录取数据的成像性能来选择较优的曲线孔径形状。Brian[28],刘浩[8]等人研究发现,在相同的孔径跨度范围上,抛物线形孔径具有比折线形孔径更优的成像性能;唐智等人[24]通过对几种典型飞行轨迹形状下的目标重构性能进行分析,得出了关于孔径设计的直观结论:采样密集、对称的孔径能够得到更好的目标估计性能。文献[29]研究了各种路径对3-D SAR波束特性的影响,认为相比于简单曲线,同心圆,螺旋圆以及随机采样都更加有利于抑制高程角的模糊。CLSAR目标的3维特征提取过程可以等效看作是参数估计问题,苏志刚等人[22, 23]通过引进参数估计中的CRLB,设计评价孔径性能的指标。理论推导证明RCS的CRLB只依赖于噪声能量和采样点数,而3维位置估计的CRLB则取决于不依赖于散射点特征的孔径参数,进而提取出独立于特征的孔径估计器(Feature independentAperture Evaluator,FAE),说明大尺寸、非线性程度越高(高阶多项式曲线)的孔径能够更优化估计性能,为孔径设计第1次提出了理论指导。
以上研究表明:CLSAR为获取更好的参数估计性能,要对平台的曲线航迹提出较高要求,大孔径、非线性程度越高的复杂孔径(如高阶多项式曲线、随机路径、螺旋线等)更利于形成“优良”的数据录取集,从而提高参数的估计精度。
5 CLSAR研究展望经过10多年的发展,CLSAR在成像算法和孔径设计研究上都取得了初步的成果,也存在着不少的问题。针对现有研究存在的问题,结合近年来信号处理的最新研究成果,本文归纳如下几个可行的CLSAR重点研究方向:
(1) 现有成像算法普遍基于RELAX的思想,根据信号表示理论的观点,RELAX方法是一种逐步迭代的局部优化型方法,实际上是匹配追踪(MatchPursuit,MP)和交替尺度法相结合的产物,能在一定程度上克服匹配追踪的弱点,但仍然脱离不了吐故纳新算法的范畴,本质上具有与匹配追踪算法类似的一步优化策略的短视效应,存在得不到全局最优解的问题。CLSAR是一个典型的不完全测量系统,由于测量数据维数小于真实信息的维数,使得由观测数据还原真实信息是个病态逆过程,不能得到关于真实信息的唯一解,存在不适定性。如果没有关于欲求解问题的先验信息,这一本质性的困难是无法克服的。稀疏信号表示寻优为此类问题提供了求解思路,作为一种新兴的信号分析方法,它以过完备函数基为基础,能从有限的观测数据中获得信号的稀疏表示,有效地挖掘信号的自然属性和本质驱动源。利用全局竞争优化的稀疏表示寻优算法(如基寻踪(Basis Pursuit,BP)方法),能有效利用先验信息,避免迭代寻优的运算复杂性,得到全局最优解。
(2) 当前成像方法只适用于理想散射点或由其组成的简单目标,CLSAR在对复杂目标进行大孔径3维观测时,为获取更全面的目标信息,需要基于更为复杂的散射模型对目标进行特征提取。对理想散射点组成的简单目标情况,其信号可以表示为3维正弦信号,这相当于将接收数据在傅里叶基下进行稀疏展开,再通过稀疏表示寻优算法进行特征提取。但对于具有更为复杂的散射机理的目标,回波中除了点散射机理外,还可能包括各种复杂散射机理,如镜面散射、谐振、发散性散射等,在傅里叶基下,得不到信号的稀疏表示,需要构造更加贴近信号自然属性的基函数来稀疏表示目标信号,从而抓住信号的本质。
(3) 目前针对孔径设计,还缺乏具有普遍理论指导意义的方法。近年来兴起的压缩感知(Compress Sensing,CS)思想[30],可以为孔径设计提供理论指导。压缩感知思想原理是基于某些信号具有可压缩或稀疏表示的本质,通过合理设计基函数和测量矩阵,突破传统Nyquist采样定理的限制,获得远小于信号维数(N)但包含足够信号特征信息的采样( $M \ll N$),并通过优化算法复原信号。该方法的关键是找出与基函数矩阵Ψ满足一定关系的可以用来恢复原信号的测量矩阵Φ。引入该思想到CLSAR的孔径设计,通过建立以孔径形状参数为自变量的系统函数矩阵Φ作为采样矩阵,结合其与基函数矩阵的相互关系可以设计Φ,进而直接设计最优孔径形状。
(4) CLSAR为获取更好的参数估计性能,要对平台的曲线航迹提出较高要求,如大孔径、非线性程度越高的复杂孔径更利于形成密集的数据录取集,从而提高参数的估计精度。然而,受平台飞行性能的限制及从安全角度考虑,过于复杂的航迹是不现实的。大孔径跨度要求长相干积累时间,在曲线飞行条件下,要长时间地控制成像所要求的运动精度和天线指向精度也是相当困难的。基于此,可以考虑将空变双/多基地3维观测方式[31, 32]与CLSAR天然的结合[28, 33]。在加入双/多基地观测这个新手段以后,将曲线孔径和双基地空变性这样两种3维成像机理有机结合起来,增加了观测几何变化的维度,可以实现变化更加复杂的数据录取曲面,有利于在有限观测角下记录更丰富的3维信息。同时,单/双基地同时观测可有效缩短曲线长度、降低单条曲线的复杂度,避免长积累时间、复杂运动下运动误差等因素对成像质量的影响,降低长曲线孔径和复杂曲线孔径的实现难度。
6结束语CLSAR因其工作模式上的灵活性、能提供目标3维重建信息等独特优势近年来受到了国内外学者的广泛关注。经过10多年的发展,CLSAR在成像算法和孔径设计研究上都取得了一定的成果,但在理论体系建立和观测手段上的一些不足制约着其进一步发展。本文的现状分析和技术展望表明,基于不完全测量系统理论建立以信号稀疏表示为基础的CLSAR理论体系,可为CLSAR的孔径设计和信号处理提供更强有力的理论依据和技术手段,而通过突破单基地观测等系统性限制,可对雷达的观测矩阵实现更多自由度的优化设计,提升采样信息量,实现更高质量的3维图像重构。
| [1] |
王建涛, 秦玉亮, 范波, 等. 曲线弹道SAR RD-Dechirp快视成像算法[J]. 系统工程与电子技术, 2013, 35(5): 940-947. Wang Jian-tao,Qin Yu-liang, Fan Bo, et al.. RD-Dechirp algorithm forcurvilinear trajectory SAR quick look imaging[J]. Systems Engineering andElectronics, 2013, 35(5): 940-947. (  1) 1)
|
| [2] |
He Feng, ChenQi, Dong Zhen, et al.. Processing of ultrahigh-resolution spacebornesliding spotlight SAR data on curved orbit[J]. IEEE Transactions onAerospace and Electronic Systems, 2013, 49(2): 819-839.
( 1) 1)
|
| [3] |
张子善. 曲线合成孔径雷达三维成像相关技术研究[D]. [硕士论文], 国防科技大学, 2009. Zhang Zi-shan.Research on the 3-D imaging technology of curvilinearSAR[D]. [Master dissertation], National University of DefenseTechnology, 2009. (  3) 3)
|
| [4] |
洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135 . Hong Wen.Progress in circular SAR imaging technique[J]. Journal of Radars, 2012,1(2): 124-135. (  3) 3)
|
| [5] |
Knaell K.Three-dimensional SAR from curvilinear apertures[C]. Proceedings of SPIE-International Society of Optical Engineering, Orlando, FL, 1994, 2230: 120-134.
( 2) 2)
|
| [6] |
Knaell K.Three-dimensional SAR from practical apertures[C]. Proceedings of SPIE-InternationalSociety of Optical Engineering, San Diego, CA, 1995, 2562: 31-41.
( 1) 1)
|
| [7] |
Knaell K.Three-dimensional SAR from curvilinear apertures[C]. Proceedings of the 1996IEEE National Radar Conference, Ann Arbor, MI, 1996: 2230-2238.
( 3) 3)
|
| [8] |
刘浩, 吴季. 基于曲线合成孔径雷达的三维目标特征提取[J]. 遥感技术与应用, 2004, 19(6): 493-497. Liu Hao and WuJi. Three dimensional target feature extraction using curvilinear synthetic apertureradar[J]. Remote Sensing Technology and Application, 2004, 19(6): 493-497. (  2) 2)
|
| [9] |
宋千, 李杨寰, 梁福来, 等. 圆迹合成孔径雷达成像分辨率分析[J]. 计算机仿真, 2011, 28(10): 18-22 . Song Qian, LiYang-huan, Liang Fu-lai, et al.. Analysis of circular SAR time-domain imagingresolution[J]. Computer Simulation, 2011, 28(10): 18-22. (  1) 1)
|
| [10] |
Li J, Bi Z, LiuZ S, et al.. Use of curvilinear SAR for three dimensional target featureextraction[J]. IEE Proceedings- Radar, Sonar and Navigation,1997, 144(5): 275-283.
( 2) 2)
|
| [11] |
Knaell K.Advances in three-dimensional SAR from practical apertures[C]. Proceedings ofSPIE-International Society of Optical Engineering, San Diego, CA, 1996, 2845: 183-193.
( 1) 1)
|
| [12] |
Knaell K.Progress in three-dimensional SAR from curvilinear apertures[C]. Proceedings ofSPIE-International Society of Optical Engineering, San Diego, CA, 1998, 3462:110-121.
( 1) 1)
|
| [13] |
Su Zhi-gang,Peng Ying-ping, and Wang Xiu-tan. Efficient algorithm for three-dimensionaltarget feature extraction via CLSAR[J]. Electronics Letters, 2004,40(15): 965-966.
( 3) 3)
|
| [14] |
Su Zhi-gang,Peng Ying-ning, and Wang Xiu-tan. Non- iterative imaging algorithm forCLSAR[C]. IEEE International Conference on Acoustics, Speech, and SignalProcessing, 2005, 2: 577-580.
( 3) 3)
|
| [15] |
Su Zhi-gang,Peng Ying-ning, and Wang Xiu-tan. Fast non- iterativeimaging algorithm for CLSAR[C]. IEEE International Radar Conference, Arlington, VA, 2005: 778-782.
( 1) 1)
|
| [16] |
苏志刚, 彭应宁, 王秀坛. 曲线合成孔径雷达中散射点三维特征提取方法[J]. 清华大学学报(自然科学版), 2005, 45(7): 947-950 . Su Zhi-gang,Peng Ying-ning, and Wang Xiu-tan. Extraction of 3-D features of scatterers incurvilinear SAR[J]. Journal of Tsinghua University (Science &Technology), 2005, 45(7): 947-950. (  1) 1)
|
| [17] |
苏志刚, 彭应宁, 王秀坛. 三维目标CLSAR成像的降维搜索算法[J]. 电子与信息学报, 2006, 28(6): 965-968. Su Zhi-gang,Peng Ying-ning, and Wang Xiu-tan. Dimension- reduced searching method for 3-D targetimaging in curvilinear SAR[J]. Journal of Electronics & Information Technology, 2006, 28(6): 965-968. (  1) 1)
|
| [18] |
Su Zhi-gang,Peng Ying-ning, and Wang Xiu-tan. Three- dimensional target features extractionmethod in curvilinear SAR with aperture errors[C]. IEEE International Symposiumon Communications and Information Technology, 2005 (ISCIT 2005), 2005, 2: 1227-1230.
( 1) 1)
|
| [19] |
Li J, Bi Z, andLiu Z S. Autofocus and feature extraction in curvilinear SAR via arelaxation-based algorithm[J]. IEE Proceedings-Radar, Sonar andNavigation, 1999, 146(4): 201-207.
( 3) 3)
|
| [20] |
Su Zhi-gang, WuRen-biao, Liu Jia-xue, et al.. A robust autofocus algorithm for the 3-Dtarget feature extraction in curvilinear SAR[C]. 2001 CIE InternationalConference on Radar, Beijing, 2001: 644-648.
( 1) 1)
|
| [21] |
吴仁彪, 苏志刚, 刘家学, 等. 一种基于CLSAR的三维目标特征提取与自聚焦新算法[J]. 遥感学报, 2002, 6(6): 490-495. Wu Ren-biao, SuZhi-gang, Liu Jia-xue, et al.. A novel autofocus and 3-D target featureextraction algorithm for curvilinear SAR[J]. Journal of Remote Sensing,2002, 6(6): 490-495. (  1) 1)
|
| [22] |
Su Zhi-gang,Peng Ying-ning, and Wang Xiu-tan. Evaluation of the aperture in the curvilinearSAR[C]. 2006 CIE International Conference on Radar, Shanghai, 2006: 1-4.
( 3) 3)
|
| [23] |
Su Zhi-gang,Peng Ying-ning, and Wang Xiu-tan. Feature- independent aperture evaluator forthe curvilinear SAR[J]. IEEE Geoscience and Remote Sensing Letters,2007, 4(2): 191-195.
( 2) 2)
|
| [24] |
Tang Zhi, LiJing-wen, Zhou Yin-qing, et al.. Research on optimal aperture for curvilinearSAR[J]. Journal of Astronautics, 2006, 27(5): 897-903.
( 3) 3)
|
| [25] |
Liu Xiang-leand Yang Ru-liang. Study of composite mode curvilinear SAR[C]. 2006 CIEInternational Conference on Radar, Shanghai, 2006: 1-4.
( 1) 1)
|
| [26] |
Su Zhi-gang, Liu Gui-ying, Peng Ying-ning, et al..RCB-based imaging method for3-D target via curvilinear SAR[C]. 9th International Conference on SignalProcessing, Beijing, 2008: 2368-2371.
( 2) 2)
|
| [27] |
庞守宝, 张晓玲, 等. 机载下视圆周SAR三维BP成像[J]. 电子科技, 2010, 23(12): 14-17. Pang Shou-bao, ZhangXiao-ling, et al.. Imaging of downward- looking 3D circleSAR by BP algorithm[J]. Electronic Science and Technology, 2010, 23(12):14-17. (  1) 1)
|
| [28] |
Brian D R andRandolph L M. Flight path strategies for 3-D scene reconstruction from BistaticSAR[J]. IEE Proceedings- Radar, Sonar and Navigation,2004, 151(3): 149-157.
( 2) 2)
|
| [29] |
Sune R J andAxelsson. Beam characteristics of three- dimensional SAR in curved or randompaths[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004,42(10): 2324-2334.
( 1) 1)
|
| [30] |
Donoho D L.Compressed sensing[J]. IEEE Transactions on Information Theory, 2006,52(4): 1289-1306.
( 1) 1)
|
| [31] |
Chemiakov M.Space-surface bistatic synthetic aperture radar-prospective and problems[C].International Radar Conference, Edinburgh, UK, 2002: 22-25.
( 1) 1)
|
| [32] |
Hu Cheng, LongTeng, and Zeng Tao. The possibility of isolated target 3-D position estimationand optimal receiver position determination in SS-BSAR[J]. Science in China Series F: Information Sciences, 2008, 51(9): 1372-1383.
( 1) 1)
|
| [33] |
Rigling B D.Signal processing strategies for bistatic synthetic aperture radar[D]. [Ph.D. dissertation], Ohio State University, 2003.
( 1) 1)
|


