② 解放军第91918部队 北京 102300
② Unit 91918 of PLA, Beijing 102300, China
波达方向(Direction Of Arrival, DOA)估计在雷达、通信等领域具有广泛的应用[1, 2, 3],但探测空间存在的相干或强相关信号会导致阵列接收数据协方差矩阵出现秩亏,信号子空间向噪声子空间扩散,导致子空间类算法估计性能下降甚至失效。同时,在弹载阵列探测系统中,对测向算法的估计精度及算法的解算实时性要求更高,因此,研究相干信源条件下高精度、低计算复杂度的新方法具有重大实际意义。
常用的解相干预处理方法可分为降维处理[4, 5, 6]和非降维处理[7, 8, 9, 10, 11, 12]两类。其中,降维处理解相干算法主要以空间平滑类算法[4](Spatial Smoothing,SS)及其改进算法[5, 6]为代表,它将传感器阵列划分为多个具有平移特性的子阵,通过子阵协方差矩阵的叠加实现协方差矩阵的秩与信源个数相等。为避免阵列孔径损失,文献[7, 8, 9]提出一类Toeplitz矩阵重构算法,通过恢复协方差矩阵的秩实现解相干,避免了空间平滑,但矩阵构造过程需要大量阵列接收数据互相关运算,计算量较大。文献[10]提出一种直接数据域取对称共轭向量解相干的方法,但要求相干信号个数不大于两个。文献[11, 12]利用高阶累积量的阵列扩展能力,基于阵列快拍数据的4阶累积量结合时间平滑处理实现相干多径的DOA估计并具有抑制高斯色噪声的能力,且估计信源个数超过阵元个数,但上述算法均建立在大量时域累计快拍的基础上,且计算复杂度高,不适用于实时性高的应用背景。
针对短时小样本条件下相干信号的DOA估计问题,相关文献较少。文献[13, 14]将坐标原点建立在阵列几何中心,利用阵列单次快拍接收数据构建Toeplitz矩阵实现了相干信号解相干,但实质上损失了阵列一半的孔径,估计误差过大。文献[15]首次提出了一种利用少快拍数进行相干积累,并结合矢量奇异值分解算法实现相干信号DOA估计的算法(CAV-SS算法),但同样存在阵列孔径损失问题。基于以上问题,本文提出一种基于相干积累矩阵重构的快速解相干算法。该算法首先基于相干积累原理对短快拍阵列接收数据进行处理,得到累积快拍矢量,然后利用该矢量第1个元素与特征矢量进行复乘,并在此基础上构建一个非降维的等效协方差矩阵,经公式推导证明,矩阵的秩与信源个数相同,与信号间相关性无关,即实现了信源的完全解相干。同时,该算法通过相干积累实现了信号能量的积累,提高了算法的抗噪性,且有效避免了阵列孔径损失,分辨率高、计算量小。
2 数据模型与问题的提出 2.1 数据模型假设$M$个各向同性阵元组成均匀线性阵列,阵元间距为$d$,阵元编号为$1,2, \cdots ,M$。$N$个远场窄带信号 ${s_k}(t)(k = 1,2, \cdots ,N)$分别以与阵列法线夹角${\theta _k}$的方向入射。阵列噪声为加性高斯白噪声,且噪声与信号相互独立。以编号1阵元为参考原点,阵列观测信号的矢量表示为:
| ${X}(t) = {\left[ {{x_1}(t) {x_2}(t) \cdots {x_M}(t)} \right]^{\rm{T}}} = {A}(\theta ){S}(t) + {N}(t)$ | (1) |
| ${A}(\theta ) = \left[ {{a}\left( {{\theta _1}} \right){\kern 1pt} \,{a}\left( {{\theta _2}} \right)\, \cdots \,{a}\left( {{\theta _N}} \right)} \right]$ | (2) |
| $a\left( {{\theta _k}} \right) = {\left[ {1\;u\left( {{\theta _k}} \right)\; \cdots \;{u^M}\left( {{\theta _k}} \right)} \right]^{\rm{T}}}, k = 1,2, \cdots ,N$ | (3) |
| $\begin{array}{l} {A}(\theta ){S}\left( {{t_1}} \right) = \left[ {{a}\left( {{\theta _1}} \right)\;{a}\left( {{\theta _2}} \right)\; \cdots \;{a}\left( {{\theta _N}} \right)} \right] {\left[ {{s_1}\left( {{t_{\rm{1}}}} \right){s_2}\left( {{t_2}} \right)\; \cdots \;{s_N}\left( {{t_1}} \right)} \right]^{\rm{T}}}\\ = \sum\limits_{k = 1}^N {{s_k}\left( {{t_1}} \right){a}\left( {{\theta _k}} \right)} \end{array}$ | (4) |
| ${X}\left( {{t_1}} \right) = {A}(\theta ){S}\left( {{t_1}} \right) + {N}\left( {{t_1}} \right) = \sum\limits_{k = 1}^N {{s_k}\left( {{t_1}} \right){a}\left( {{\theta _k}} \right)} + {N}\left( {{t_1}} \right)$ | (5) |
由式(5)可知,每一次快拍矢量均可表示为阵列流型矩阵${A}(\theta )$中所有导向矢量的一个线性组合,即含有信源入射角度所有信息,而多次快拍数据经过相干积累能够提高信噪比[15],文献[15]即利用该性质提出了相干积累矢量平滑算法(CAV-SS)。下面对该算法进行简介。
假设信号载频$\omega$已知,首先构造K维相干积累列向量
| $F = {\left[ {1\;\exp \left( { - {\text{j}}\omega T} \right) \exp \left( { - {\text{j}}2\omega T} \right)\; \cdots \;\exp \left( { - {\text{j}}(K - 1)\omega T} \right)} \right]^{\text{T}}}$ | (6) |
| $V = \left[ {X\left( {{t_1}} \right)\;X\left( {{t_2}} \right)\; \cdots \;X\left( {{t_K}} \right)} \right]F$ | (7) |
由于F频率与信号载频相同,则能对信号进行能量积累,则累积快拍相较于一次快拍数据能够有效提高信噪比。然后,利用累积快拍矢量$V$构造式(7)中前后向空间平滑矩阵
| $Y = \left[ \begin{array}{l} V(1) \qquad {V^{\rm{H}}}(p) \qquad V(2) \quad {V^{\rm{H}}}(p + 1) \cdots V(M - p + 1) \quad \; {V^{\rm{H}}}(M)\\ V(2) \quad {V^{\rm{H}}}(p - 1) \quad \; V(3) \qquad {V^{\rm{H}}}(p) \; \cdots \; V(M - p + 2) \quad {V^{\rm{H}}}(M - 1)\\ \quad \vdots \qquad \qquad \begin{array}{*{20}{c}} { \vdots \qquad \qquad \begin{array}{*{20}{c}} { \vdots \qquad \qquad \vdots \qquad \; \ddots \qquad \vdots } \end{array} \qquad \qquad \qquad \vdots } \end{array}\\ V(p) \qquad {V^{\rm{H}}}(1) \quad V(p + 1) \quad \; {V^{\rm{H}}}(2)\quad \cdots \quad V(M) \qquad {V^{\rm{H}}}(M - p + 1) \end{array} \right]$ | (8) |
通过对该矩阵进行一次奇异值分解结合常规子空间类算法即可实现对入射信源的DOA估计,为确保${\text{rank}}(Y) = N, p$的选择范围为$N < p < (M - N/2 + 1)$,即算法存在较大的阵列孔径损失。
3 相干积累矩阵重构解相干算法首先,通过相干积累得到累积快拍矢量,即将式(5)代入至式(7)中,则$M \times 1$维累积快拍矢量V可展开为:
| $ V = \left[ {X\left( {{t_1}} \right)X\left( {{t_2}} \right)\; \cdots \;X\left( {{t_K}} \right)} \right]F = \sum\limits_{i = 1}^K {X\left( {{t_i}} \right)F(i)} \\ \; \;= \sum\limits_{k = 1}^N {\sum\limits_{i = 1}^K {{a}\left( {{\theta _k}} \right){s_k}\left( {{t_i}} \right)F(i)} } + {N}(t) \\ $ | (9) |
其中,$F(i)$表示向量F的第$i$个元素,${N}(t) = \left[ {{N}\left( {{t_1}} \right) \;{N}\left( {{t_2}} \right) \; \cdots \;{N}\left( {{t_K}} \right)} \right]F$。由于${s_k}({t_{i + n}}) = {s_k}({t_i}) \cdot \exp ({\text{j}}(n - 1)\omega T)$,则满足$\sum\nolimits_{i = 1}^K {{s_k}({t_i})F(i)} = K{s_k}({t_1})$,式(9)可简化为:
| ${V} = \sum\limits_{k = 1}^N {K{s_k}\left( {{t_1}} \right){a}\left( {{\theta _k}} \right)} + {N}(t)$ | (10) |
将式(10)所示累积快拍矢量与式(5)所示单次快拍数据进行对比可知,累积快拍矢量不仅可表示为阵列流型矩阵${A}(\theta )$中所有导向矢量的线性组合,且其中信号分量幅值增强了$K$倍,而噪声能量无法得到累积,因此提高了信噪比。矢量${V}$的第$m$个元素可表示为:
| ${V}(m) = \sum\limits_{k = 1}^N {K{s_k}(t){u^{m - 1}}} + {n_m}(t), m = 1,2, \cdots ,M$ | (11) |
定义$M \times 1$维特征矢量$\widetilde {V}$,该矢量的第$m$个元素定义如下:
| $\widetilde {V}(m) = {V}(m){{V}^*}(1)$ | (12) |
| $\widetilde {R} = \left[ {\begin{array}{*{20}{c}} {\widetilde {V}(1)}&{{{\widetilde {V}}^*}(2)}& \cdots &{{{\widetilde {V}}^*}(M)} \\ {\widetilde {V}(2)}&{\widetilde {V}(1)}& \cdots &{{{\widetilde {V}}^*}(M - 1)} \\ \vdots & \vdots & \ddots & \vdots \\ {\widetilde {V}(M)}&{\widetilde {V}(M - 1)}& \cdots &{\widetilde {V}(1)} \end{array}} \right]$ | (13) |
下面证明矩阵$\widetilde {R}$可分解为阵列数据协方差矩阵形式,且矩阵的秩仅与信源个数有关,与信源间的相干性无关。证明如下:
结合式(11)对$\widetilde {V}(m)$进行如下分解:
| $\begin{array}{l} \widetilde {V}(m) = {V}(m){{V}^*}(1) = \left( {\sum\limits_{i = 1}^N {K{s_i}(t){{\rm{e}}^{ - {\rm{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _i}}} + {n_m}(t)} } \right)\left( {\sum\limits_{j = 1}^N {Ks_j^*(t){\rm{ + }}n_1^*(t)} } \right)\\ = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{K^2}{s_i}(t)s_j^*(t){{\rm{e}}^{ - {\rm{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _i}}}} } + {\sigma ^2}\delta (m,1)\\ = \left[ {{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _1}}}\;{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _2}}}\; \cdots \;{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _N}}}} \right]\\{G}\left[ { \begin{array}{*{20}{c}} {1 }\\ {1 }\\ { \vdots }\\ {1 } \end{array}} \right] + {\sigma ^2}\delta (m,1) = {{a}_m}(\theta ){Ga}_1^{\mathop{\rm H}\nolimits} (\theta ) + {\sigma ^2}\delta (m,1) \end{array}$ |
| (14) |
| ${g_k} = \sum\limits_{j = 1}^N {{K^2}s_j^*(t)} s_k^{}(t), k = 1,2, \cdots ,N$ | (15) |
同理,$\widetilde {V}(m)$的共轭可分解为:
| $\begin{gathered} {\widetilde {V}^*}(m) = {V}(1){{V}^*}(m) = \left( {\sum\limits_{j = 1}^N {Ks_j^{}(t){\text{ + }}n_1^{}(t)} } \right) \hfill \\ \quad \quad \quad \cdot \left( {\sum\limits_{i = 1}^N {Ks_i^*(t){{\text{e}}^{\operatorname{j} \frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _i}}} + n_m^*(t)} } \right) \hfill \\ \quad \quad \quad \quad \quad \quad \quad= \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{K^2}{s_j}(t)s_i^*(t){{\text{e}}^{{\text{j}}\frac{{2\bf {\pi} }}{\lambda }(m - 1)d\sin {\theta _i}}}} } + {\sigma ^2}\delta (m,1) \hfill \\ \end{gathered} $ | (16) |
| $\begin{array}{c} {\widetilde {V}^*}(m) = [1,1, \cdots ,1]{G}\left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\rm{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _1}}}}\\ {{{\rm{e}}^{{\rm{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _2}}}}\\ \vdots \\ {{{\rm{e}}^{{\rm{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _N}}}} \end{array}} \right] + {\sigma ^2}\delta (m,1)\\ = {{a}_1}(\theta ){Ga}_m^{\mathop{\rm H}\nolimits} (\theta ) + {\sigma ^2}\delta (m,1) \end{array}$ | (17) |
| $\widetilde {R} = {A}(\theta )G{{A}^{\mathop{\rm H}\nolimits} }(\theta ) + {\sigma ^2}{{I}_{M \times M}}$ | (18) |
进一步对式(18)进行如下证明:
阵列流行矩阵${A}(\theta )$可表示为:
| ${A}(\theta ) = \left[ \begin{gathered} {{a}_1}(\theta ) \\ {{a}_2}(\theta ) \\ \vdots \\ {{a}_M}(\theta ) \\ \end{gathered} \right]$ | (19) |
其中,${{a}_m}(\theta ) = \left[ {{{\text{e}}^{ - {\text{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _1}}}\; \cdots \;{{\text{e}}^{ - {\text{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _N}}}} \right]$表示阵列流型矩阵${A}(\theta )$第$m$行,则式(18)等号右侧可表示为:
| $\begin{array}{l} {A}(\theta )G{{A}^{\mathop{\rm H}\nolimits} }(\theta ) + {\sigma ^2}{{I}_{M \times M}} = \left[ \begin{array}{c} {{a}_1}(\theta )\\ {{a}_2}(\theta )\\ \vdots \\ {{a}_M}(\theta ) \end{array} \right]G\left[ {{a}_{\rm{1}}^{\rm{H}}(\theta )\;\;{a}_{\rm{2}}^{\rm{H}}(\theta )\;\; \cdots \;\;{a}_M^{\rm{H}}(\theta )} \right] + {\sigma ^2}{{I}_{M \times M}}\\ = \left[ \begin{array}{l} {{a}_1}(\theta )G{a}_{\rm{1}}^{\rm{H}}(\theta ) + {\sigma ^2}\quad {{a}_1}(\theta )G{a}_{\rm{2}}^{\rm{H}}(\theta )\quad \quad \cdots \;{{a}_1}(\theta )G{a}_M^{\rm{H}}(\theta )\\ {{a}_2}(\theta )G{a}_1^{\rm{H}}(\theta ) {{a}_2}(\theta )G{a}_2^{\rm{H}}(\theta ) + {\sigma ^2} \cdots {{a}_2}(\theta )G{a}_M^{\rm{H}}(\theta )\quad \\ \quad \quad \vdots \quad \quad \quad \quad \quad \quad \vdots \quad \quad \quad \ddots \quad \quad \quad \quad \vdots \\ {{a}_M}(\theta )G{a}_1^{\rm{H}}(\theta ) {{a}_M}(\theta )G{a}_2^{\rm{H}}(\theta )\quad \quad \cdots {{a}_M}(\theta )G{a}_M^{\rm{H}}(\theta ) + {\sigma ^2} \end{array} \right] \end{array}$ | (20) |
考虑式(20)中对角元素,${{a}_m}(\theta )G{a}_m^{\text{H}}(\theta ), m = 1,2, \cdots ,M$可表示为:
| $\begin{gathered} {{a}_m}(\theta ){Ga}_m^{\text{H}}(\theta ) = \left[ {{{\text{e}}^{ - {\text{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _1}}}\; \cdots \;{{\text{e}}^{ - {\text{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _N}}}} \right] \\ \cdot {G}\left[ \begin{gathered} {{\text{e}}^{{\text{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _1}}} \\ \vdots \\ {{\text{e}}^{{\text{j}}\frac{{2\pi }}{\lambda }(m - 1)d\sin {\theta _N}}} \\ \end{gathered} \right] \\ = \sum\limits_{k = 1}^N {{g_i}} \\ \end{gathered} $ | (21) |
由式(21)可以得知,式(20)所有对角元素相等,均可由$\widetilde {V}(1) = {{a}_1}(\theta ){Ga}_{\text{1}}^{\text{H}}(\theta ) + {\sigma ^2}\delta (m,1)$表示。此时,将式(14),式(17)代入至式(20),即可证明式(18)等式左右两侧相等。 证毕
显然,无论信号间是否相关,对角阵$G$的对角元素均不为零,且${A}(\theta )$为列满秩矩阵,则${\text{rank(}}{G}{\text{) = }}N$,即实现了相干信源的完全解相干。由式(18)形式可知,通过对矩阵$\widetilde {R}$进行一次特征分解并结合常规子空间类算法即可实现相干信源的DOA估计。由于等效协方差矩阵$\widetilde {R}$为$M \times M$维矩阵,则$M$阵元均匀线阵最多可估计$M - 1$个相干信源,即算法无孔径损失。且对角阵$G$的对角元素形式(式(15))可以看出,当信号完全相干时,${g_k}$为所有入射信号叠加功率的${K^2}$倍,即等效协方差矩阵$\widetilde {R}$的构造大幅增大了信号能量,提高了信噪比,确保了算法在低信噪比下能够保持稳健的估计性能。
利用本文进行相干信号DOA估计的具体步骤如下:
步骤1 获取阵列观测快拍数据${X}(t)$;
步骤2 根据式(9)对${X}(t)$进行相干积累,得到累积快拍矢量$\widetilde X(t)$;
步骤3 根据式(12)构造特征矢量$\widetilde {V}$;
步骤4 根据式(13)构造等效协方差矩阵$\widetilde {R}$;
步骤5 对矩阵$\widetilde {R}$进行特征分解,结合常规子空间算法得到信源DOA。
由算法具体步骤可知,本文算法的计算量主要集中在步骤2和步骤5,其中式(9)累积快拍矢量构建约需${\text{O}}(KM)$次复乘运算,对式(13)构建的矩阵$\widetilde {R}$进行特征分解约需${\text{O}}({M^3})$次复乘运算,较之CAV- SS算法中对降维矩阵进行矢量奇异值分解的运算量有所增加,但避免了阵列孔径损失;较之MSS算法[5],本文算法计算量则降幅较大,MSS算法需要对大量时域累积快拍进行互相关及空间平滑处理,需要约${\text{O}}({(M - P)^2}L + {(M - P)^3})$次复乘运算($P$为平滑次数,$L$为快拍次数),且MSS算法孔径损失严重,分辨率低。
4 数值仿真分析为验证算法的有效性,设计如下仿真试验。将本文算法与修正的空间平滑MSS算法[5]及同样基于相干积累的CAV-SS算法[15]进行对比,分析算法的优点和局限性。
仿真1 验证算法的解相干性能
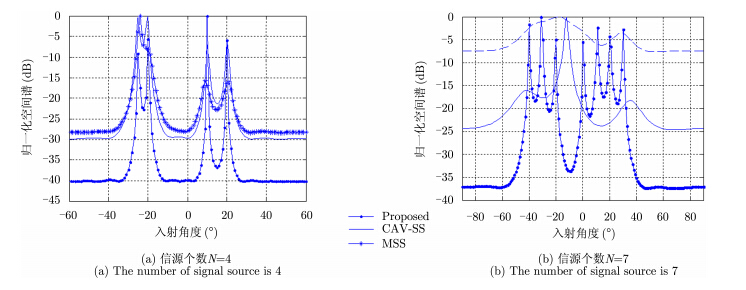
考虑 4 个远场窄带信号,频率${f_0} = 20 \,{\text{MHz}}$,信号形式为${s_1}(t) = {s_2}(t) = \text{exp}(2\pi {f_0}t),{s_3}(t) = \text{exp}(2\pi {f_0}t + \pi /6),{s_4}(t) = \text{exp}(2\pi {f_0}t + \pi /3)$,入射方向分别为-25°,-20°, 10°, 20°,采样频率为100 MHz。阵元个数$M$=8,阵元间距$d = \lambda /2,\lambda $为信号波长,快拍次数为100次,相干积累次数$K$=30,信噪比SNR=5 dB,结合MUSIC算法得到本文算法、MSS算法及CAV-SS算法的空间谱曲线,如图 1(a)。仿真条件不变,考虑7个远场窄带信号分别从角度-40°,-30°,-20°, 0°, 10°, 20°, 30°入射至8阵元均匀线阵,得到3种算法的空间谱曲线,如图 1(b)。
|
图 1 相干信号DOA估计性能 Fig.1 DOA estimation results of coherent signals |
由信号形式可知,信号1与信号2为相干信号,信号3和信号4为相关信号,且与信号1和信号2是相关的。由图 1(a)可知,本文算法能够实现对4个信源的解相干,且算法的估计精度高于CAV-SS算法及MSS算法,尤其当入射角度接近时(-25°与-20°)表现得更加明显。分析原因,本文算法所构造的等效协方差矩阵的秩与信源个数相等,与信源间相关性无关,因此实现了信号的完全解相干,充分利用了阵列孔径。而CAV-SS算法和MSS算法的实质是对数据协方差矩阵的秩进行恢复的过程,其解相干性能是以降低阵列自由度为代价的,估计性能与本文算法相比较低。由图 1(b)可知,本文算法$M$阵元均匀线阵最多可估计$M - 1$个相干信源,而对比算法此时已经无法对所有信号DOA进行估计。
仿真 2 验证算法的角度分辨力
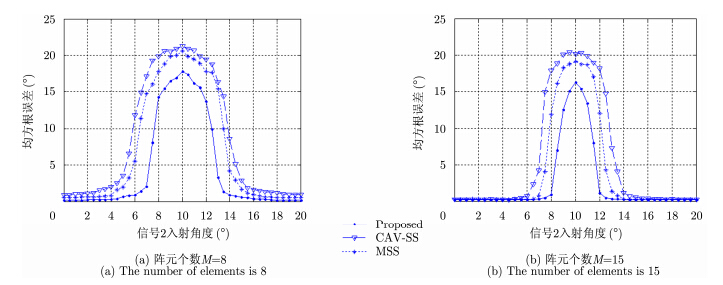
考虑仿真1中的2个远场窄带相干信号 ${s_1}(t)$和${s_2}(t)$入射至8阵元均匀线阵,固定信号1的入射角角度为10°,改变信号2的入射角度,使其从0°至20°区间以0.5°为步长步进,快拍次数为100次,相干积累次数$K$=30,信噪比SNR=5 dB,每个入射角度下进行200次Monte-Carlo统计试验,验证本文算法、CAV-SS算法及MSS算法的角度分辨力。仅改变阵元个数,分别得到8阵元(图 2(a))和15阵元(图 2(b))均匀线阵时算法DOA估计均方根误差随信号2入射角度变化曲线。
由图 2可知,所有算法的DOA估计均方根误差均随角度差增大而递减,且本文算法在相同角度差条件下的均方根误差相较于CAV-SS算法、MSS算法更小。分析原因,本文算法在解相干的过程中未损失阵列自由度,而CAV-SS算法和MSS算法在信号协方差矩阵恢复秩的过程中均存在不同程度孔径损失,降低了算法的估计性能。另一方面,将不同阵元数下的DOA估计性能进行对比可知,当阵元个数增大时,阵列的角度分辨力与阵列孔径大小具有正比关系。
|
图 2 DOA估计误差随入射角度变化曲线 Fig.2 RMSE curve of DOA estimation with incident angle |
仿真3 验证算法的估计性能随信噪比变化关系
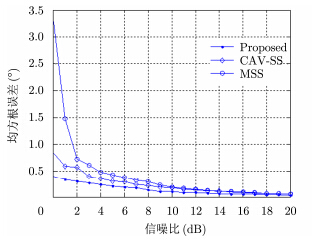
考虑仿真图 1(a)中4个信号,分别以同样角度入射至15阵元均匀线阵,快拍次数为100次,相干积累次数$K$=30,改变入射信号的信噪比,使其从0 dB至20 dB区间以1 dB为步长步进,每个信噪比下进行200次Monte-Carlo统计试验,验证本文算法、CAV-SS算法及MSS算法DOA估计的均方根误差(Root-Mean-Square Error,RMSE)随信噪比的变化关系。DOA估计的RMSE定义为:
${E_{{\text{rms}}}} = \frac{1}{N}\sum\limits_{k = 1}^N {\sqrt {E\left\{ {{{\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } }_k} - {\theta _k}} \right)}^2}} \right\}} } $
式中,$N$为信源个数,${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } _k}$为估计值,${\theta _k}$为标称值。由图 3可知,算法的估计均方根误差均随信噪比的增大而递减,在同一信噪比下,本文算法的DOA估计均方根误差低于CAV-SS算法,MSS算法的估计误差最高。分析原因,本文算法及CAV-SS算法均在解相干矩阵的构造过程中对信号能量进行了积累,而噪声分量却无法进行能力叠加,因此提高了数据的信噪比,而本文算法在等效协方差矩阵的构造过程中通过对累积快拍矢量处理避免了阵列孔径损失,因此本文算法的估计性能高于CAV-SS算法,而基于空间平滑原理的MSS算法不存在能量累积,且存在较大阵列孔径损失,因此估计均方根误差最大。
|
图 3 DOA估计误差随信噪比变化曲线 Fig.3 RMSE curve of DOA estimation with SNR |
仿真 4 验证算法的估计性能随累积快拍次数及信噪比的变化关系
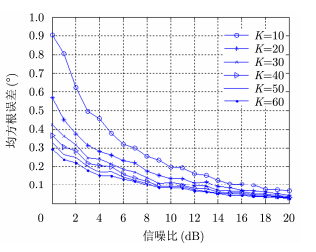
仿真参数设定与仿真3相同,仅改变算法相干积累过程中所需的累积快拍次数,使累积快拍次数分别为$K = 10, 20, \cdots , 60$,改变信噪比,使其从0 dB至20 dB区间以1 dB为步长步进,每个信噪比下进行200次Monte-Carlo统计试验,验证本文算法在不同累积快拍数下的估计性能随信噪比的变化关系。由图 4可知,在同一信噪比条件下,本文算法的估计性能随累积快拍次数的增加而不断提高,但当快拍次数大于30后,累积快拍次数的增加对算法的估计性能的影响逐渐减小。
|
图 4 DOA估计误差随累积快拍次数及信噪比变化曲线 Fig.4 RMSE curve of DOA estimation with accumulation snapshot and SNR |
针对短时小样本条件下的相干信号DOA估计问题,本文提出一种基于相干积累矩阵重构的非降维快速解相干算法。算法通过对少量阵列接收快拍数据进行相干积累,得到累积快拍矢量,实现了信号能量的累积,提高了信噪比,同时通过公式推导证明了基于累积快拍矢量所构造的非降维等效协方差矩阵的秩与信源个数相等,即实现了相干信源的完全解相干。相较于常规空间平滑算法,本文算法无需平滑处理,计算量小,且无孔径损失,分辨率高。如何将本文算法思想应用至多阵列误差下的阵列空间谱估计领域是下一步的研究重点。
| [1] |
Zheng Z, Li G J,and Teng Y L. Simplified estimationof 2D DOA for coherently distributed sources[J]. Wireless Peronal Communications,2012, 62(4): 907-922.
( 1) 1)
|
| [2] |
Kassis C E,Picheral J, and Mokbel C. Advantages of nonuniform arrays using root-MUSIC[J]. Signal Processing, 2010, 90(2): 689-695.
( 1) 1)
|
| [3] |
蒋柏峰, 吕晓德, 向茂生. 基于广义MUSIC算法的低仰角估计新方法[J]. 雷达学报, 2013, 2(4): 422-429. Jiang Bai-feng,Lü Xiao-de, and Xiang Mao-sheng. A new low-elevation estimation method based ona general MUSIC algorithm[J]. Journal of Radars, 2013, 2(4): 422-429. (  1) 1)
|
| [4] |
Pillai S U and Kwon B H. Forward-backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1989, 37(1): 8-15.
( 2) 2)
|
| [5] |
Williams R T, Prasad S, Mahalanabis A K, et al..An improved spatial smoothing technique for bearing estimation in a multi path environment[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1988, 36(4):425-432.
( 4) 4)
|
| [6] |
Gu J F, Wei P,and Tai H M, 2-D direction-of-arrival estimation of coherent signals using cross-correlation matrix[J]. Signal Processing, 2008, 88(1): 75-85.
( 2) 2)
|
| [7] |
高书彦, 陈辉, 王永良, 等. 基于均匀圆阵的模式空间矩阵重构算法[J]. 电子与信息学报, 2007, 29(12): 2832-2835 . Gao Shu-yan,Chen Hui, Wang Yong-liang, et al.. The MODE-TOEP algorithm based on uniform circular array[J]. Journal of Electronics & InformationTechnology, 2007, 29(12): 2832-2835. (  2) 2)
|
| [8] |
Kareem A J,Hyuck M K, and Nizar T. Modified UCA-ESPRIT for estimating DOA of coherent signals using one snapshot[C]. Proceedings of the Vehicular Technology Conference, Singapore, 2008: 126-131.
( 2) 2)
|
| [9] |
谢菊兰, 李会勇, 何子述. 均匀圆阵相干信源DOA估计的差分算法[J]. 电子科技大学学报, 2012, 41(4): 516-521 . Xie Ju-lan, Li Hui-yong, and He Zi-shu. DOA estimation of coherent sources using difference algorithm with the uniform circular arrays[J]. Journal of University ofElectronic Science and Technology of China, 2012, 41(4): 516-521. (  2) 2)
|
| [10] |
袁晓东, 万建伟, 程翥, 等. 基于直接数据域自适应算法的相干信号DOA估计[J]. 国防科技大学学报, 2012, 34(3): 131-135. Yuan Xiao-dong,Wan Jian-wei, Cheng Zhe, et al. DOA estimation of correlated signals based on the adaptive algorithm in direct data domain[J].Journal of National University of Defense Technology, 2012,34(3): 131-135. (  2) 2)
|
| [11] |
周围, 朱联祥, 周正中, 等. 相干多径环境下信号空间特征及波达方向估计[J]. 电波科学学报, 2007, 22(4): 685-691. Zhou Wei, Zhu Lian-xiang, Zhou Zheng-zhong, et al. Estimation of spatial signature and direction of arrivals for signals in coherent multipath environment[J]. ChineseJournal of Radio Science, 2007, 22(4): 685-691. (  2) 2)
|
| [12] |
景小荣, 隋伟伟, 周围. 基于四阶累积量和时间平滑的相干信号DOA估计[J]. 系统工程与电子技术, 2012, 34(4): 789-795. Jing Xiao-rong,Sui Wei-wei, and Zhou Wei. DOA estimation of coherent signals based on fourth-order cumulant and temporal smoothing[J]. Systems Engineering and Electronics, 2012, 34(4): 789-795. (  2) 2)
|
| [13] |
王凌, 李国林, 孟晶, 等. 用一次快拍数据实现二维完全解相干和解互耦[J]. 系统工程与电子技术, 2012, 34(11): 2208-2214. Wang Ling, Li Guo-Lin, Meng Jing, et al.. Two-dimensional decorrelation and decoupling using single snapshot[J]. Systems Engineering and Electronics, 2012,34(11): 2208-2214. (  1) 1)
|
| [14] |
王凌, 李国林, 谢鑫. 互耦效应下用单快拍数据实现相干信源完全解相干和解耦合[J]. 电子与信息学报, 2012, 34(10): 2532-2536 . Wang Ling, Li Guo-lin, and Xie Xin. Decorrelation and decoupling of coherent signals in the presence of mutual coupling using single snapshot[J]. Journal of Electronics & Information Technology, 2012, 34(10): 2532-2536. (  1) 1)
|
| [15] |
李涛, 李国林, 徐珩, 等. 采用相干积累矢量平滑实现小样本信号解相干[J]. 西安电子科技大学学报, 2011, 38(6): 113-116. Li Tao, Li Guo-lin,Xu Heng, et al.. Small sample signals’ decorrelation using the coherent accumulation vector’ spatial smoothing[J]. Journal of Xidian University, 2011, 38(6): 113-116. (  4) 4)
|


