② 微波成像技术重点实验室 北京 100190
② Science and Technology on Microwave Imaging Laboratory, Beijing 100190, China
目标的雷达散射截面或称雷达截面(RadarCross Section, RCS)是反映目标电磁散射特性的重要参数,一般有3种测试方法:外场测试[1]、紧缩场测试[2, 3]以及近场测试[4, 5, 6]。外场测试占地面积大,易受外界环境等因素的影响,紧缩场的设备运行以及维护费用较高,空间利用率不高。文献[7]给出了复杂散射体的平面近场扫描RCS测试技术,但数据处理比较复杂。
近年来出现了一种基于近场成像的目标RCS测试新方法[8, 9]。该类方法先得到目标的雷达散射图像,雷达散射图像表示目标的等效散射中心分布,再通过这些局部等效散射中心的散射场叠加获得远处散射场,最后根据散射截面的定义得到目标的RCS值。目前的文章基本上都是讨论单站圆迹近场成像的RCS测量原理[10, 11, 12],与传统的近场测量方法相比,新的近场测量方法除能得到RCS值外,还可获得目标的雷达散射图像,而且数据处理也较为简单,但圆迹扫描亦有其缺点:(1)只能得到2维圆迹平面角域上的RCS值,无法得到3维立体角域的RCS值;(2)对被测体目标的垂直尺寸(与圆迹平面垂直方向上的尺寸)有一定的限制[11],如果被测目标的垂直尺寸(与圆迹平面垂直方向上的尺寸)较大时,圆迹扫描是不够的,需进行圆柱扫描才能获得较为可靠的远场RCS值。较少文献涉及基于圆柱扫描的RCS测试研究[13]。文献[13]针对圆迹扫描的第2个缺点,通过简单的变量代换直接给出一种3维聚焦函数,该聚焦函数要求定标体必须位于成像的中心位置上,如果不在中心位置上,则无法使用文献[13]的相关公式,因此其聚焦函数缺乏通用性。此外,文献[13]得到的仍是2维圆迹平面角域的RCS值,基于以上两点其缺乏实用性。本文以理想的点散射中心模型(即假设目标是由各向同性的等效散射中心组成)为核心假设,通过详细的理论推导给出了一种具有通用性的基于柱面扫描近场成像的RCS测量方法,该方法对定标体的位置没有严格要求,而且能得到目标的3维立体角域的RCS值。本文结构安排如下:第2节着重提出一种基于柱面扫描3维近场成像的RCS测量方法;第3节给出仿真结果,验证了方法的可行性;第4节则是全文的总结。
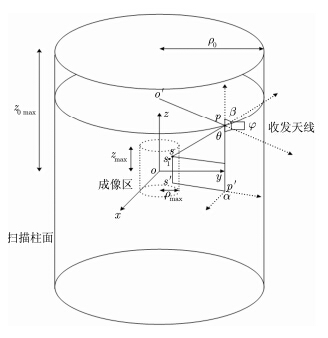
2 基于柱面扫描3维近场成像的RCS测量原理将被测目标认为由一系列局部位置上的等效散射点组成,基于电小尺寸散射体散射系数的特征,假设这些散射源的等效散射系数与频率的平方成正比[14],即目标的雷达图像是$psi \left( {x,y,z} \right)$,则相应位置上的散射系数$\gamma \left( {x,y,z,k} \right) = {k^2}\psi \left( {x,y,z} \right),\psi \left( {x,y,z} \right)$与频率无关。柱面扫描的测量示意图如图 1所示。
|
图 1 柱面扫描测量示意图 Fig.1 Sketch map of measurementconfiguration |
图 1中大的圆柱表面代表扫描区域,小的圆柱代表成像区,成像区应完全包围被测目标。${s_1}$点$\left( {{\rho _1},{\phi _1},{z_1}} \right)$散射系数为$\gamma \left( {\rho ,\phi ,z} \right) = C{k^2}\delta \left( {\rho - {\rho _1}} \right) \cdot \delta \left( {\phi - {\phi _1}} \right)\delta \left( {z - {z_1}} \right)$的散射点在方向图为$F\left( {{\beta _1},{\varphi _1}} \right)$的收发天线处产生的散射场(天线接收到的散射场):
| ${{\bf{E}}_s}\left( {k,{\rho _0},{\phi _0},{z_0}} \right) = Q\left( k \right){F^2}\left( {{\beta _1},{\varphi _1}} \right)C{k^2}\frac{{{{\rm{e}}^{ - {\rm{j}}2k{d_1}}}}}{{2\sqrt \pi d_1^2}}$ | (1) |
$\begin{array}{l} {d_1} = \left| {{r_1} - {r_0}} \right| = \left[ {{{\left( {{\rho _1}\cos {\phi _1} - {\rho _0}\cos {\phi _0}} \right)}^2}} \right.\\ {\left. { + {{\left( {{\rho _1}\cos {\phi _1} - {\rho _0}\cos {\phi _0}} \right)}^2} + {{\left( {{z_0} - {z_1}} \right)}^2}} \right]^{1/2}} \end{array}$
$Q\left( k \right)$是频率依赖因子,${\beta _1}$表示矢量${s_1}p$与正z轴矢量的夹角,${\varphi _1}$代表矢量${s_1}p$与$o'p$的夹角,${r_1}$代表$o{s_1}$矢量,${r_0}$表示$op$矢量。
假设像函数的表达式如下:
| $\begin{array}{l} \psi \left( {\rho ,\phi ,z} \right) = \int_0^\infty {{\rm{d}}k\int_0^{2\pi } {{\rm{d}}{\phi _0}\int_{ - \infty }^{ + \infty } {{\rm{d}}{z_0}} } } \\ \cdot {E_s}\left( {k,{\rho _0},{\phi _0},{z_0}} \right)F\left( {r,{r_0},k} \right) \end{array}$ | (2) |
接下来确定聚焦函数$F\left( {r,{r_0},k} \right)$的表达式。类似圆迹的聚焦函数[14],3维柱面的聚焦函数也与天线的方向图、场点与源点之间的距离有关,定义其表达式如下:
| $F\left( {r,{r_0},k} \right) = g\left( {r,{r_0},k} \right)\frac{{{{\left| {r - {r_0}} \right|}^2}}}{{Q\left( k \right){F^2}\left( {\beta ,\varphi } \right)}}{{\rm{e}}^{{\rm{j}}2k\left| {r - {r_0}} \right|}}$ | (3) |
其中$g\left( {r,{r_0},k} \right)$是修正函数,将式(3)代入式(2)可得:
| $\begin{array}{l} \psi \left( {\rho ,\phi ,z} \right) = \frac{C}{{2\sqrt \pi }}\int_0^\infty {{\rm{d}}k\int_0^{2\pi } {{\rm{d}}{\phi _0}\int_{ - \infty }^{ + \infty } {{\rm{d}}{z_0}g\left( {r,{r_0},k} \right)} } } \\ \cdot \frac{{{F^2}\left( {{\beta _1},{\varphi _1}} \right)}}{{{F^2}\left( {\beta ,\varphi } \right)}} \cdot \frac{{{{\left| {r - {r_0}} \right|}^2}}}{{{{\left| {{r_1} - {r_0}} \right|}^2}}} \cdot {{\rm{e}}^{{\rm{j}}2k\left( {\left| {r - {r_0}} \right| - \left| {{r_1} - {r_0}} \right|} \right)}}{k^2} \end{array}$ | (4) |
其中β表示矢量$sp$与正z轴矢量的夹角,$\varphi $代表矢量$sp$与$o'p$的夹角,$r$代表$os$矢量。当r在r1附近时也即是图中的$s$点趋近于${s_1}$点时,
| $\begin{array}{l} \left| {r - {r_0}} \right| - \left| {{r_1} - {r_0}} \right| \approx \left( {{x_1} - x} \right)\sin \beta \cos \alpha + \left( {{y_1} - y} \right)\\ \cdot \sin \beta \sin \alpha + \left( {{z_1} - z} \right)\cos \beta \end{array}$ | (5) |
令${k_x} = 2k\sin \beta \cos \alpha , {k_y} = 2k\sin \beta \sin \alpha , {k_z} = 2k\cos \beta ,\alpha $表示$sp$矢量在xoy平面的投影矢量$s'p'$与正x轴方向的夹角,则式(4)整理为:
| $\psi \left( {\rho ,\phi ,z} \right) = \frac{C}{{2\sqrt \pi }}\int_0^\infty {{\rm{d}}k\int_0^{2\pi } {{\rm{d}}{\phi _0}\int_{ - \infty }^{ + \infty } {{\rm{d}}{z_0}g\left( {r,{r_0},k} \right)} } } \cdot {{\rm{e}}^{{\rm{j}}\left[ {{k_x}\left( {{x_1} - x} \right) + {k_y}\left( {{y_1} - y} \right) + {k_z}\left( {{z_1} - z} \right)} \right]}}{k^2}$ | (6) |
由3阶雅克比行列式可得:
| $\psi \left( {\rho ,\phi ,z} \right) = \frac{C}{{2\sqrt \pi }}\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {{k^2}} } } \cdot \frac{{{{\left| {r - {r_0}} \right|}^3}}}{{8{k^2}{\rho _0}\left( {{\rho _0} - \rho \cos \left( {{\phi _0} - \phi } \right)} \right)}}g\left( {r,{r_0},k} \right) \\\cdot {{\rm{e}}^{{\rm{j}}\left[ {{k_x}\left( {{x_1} - x} \right) + {k_y}\left( {{y_1} - y} \right) + {k_z}\left( {{z_1} - z} \right)} \right]}}{\rm{d}}{k_x}{\rm{d}}{k_y}{\rm{d}}{k_z}$ | (7) |
令修正函数$g\left( {r,{r_0},k} \right) = \frac{{2{\rho _0}\left( {{\rho _0} - \rho \cos \left( {{\phi _0} - \phi } \right)} \right)}}{{{\pi ^{5/2}}{{\left| {r - {r_0}} \right|}^3}}}$,则式(7)转变为:
| $\begin{array}{c} \psi \left( {\rho ,\phi ,z} \right) = \frac{C}{{{{\left( {2\pi } \right)}^3}}}\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {{{\rm{e}}^{{\rm{j}}\left[ {{k_x}\left( {{x_1} - x} \right) + {k_y}\left( {{y_1} - y} \right) + {k_z}\left( {{z_1} - z} \right)} \right]}}} } } {\rm{d}}{k_x}{\rm{d}}{k_y}{\rm{d}}{k_z}\\ = C\delta \left( {x - {x_1}} \right)\delta \left( {y - {y_1}} \right)\delta \left( {z - {z_1}} \right) = C\delta \left( {\rho - {\rho _1}} \right)\delta \left( {\phi - {\phi _1}} \right)\delta \left( {z - {z_1}} \right) \end{array}$ | (8) |
故由式(8)可得聚焦函数的表达式为:
| $F\left( {r,{r_0},k} \right) = g\left( {r,{r_0},k} \right)\frac{{{{\left| {r - {r_0}} \right|}^2}}}{{Q\left( k \right){F^2}\left( {\beta ,\gamma } \right)}}{{\rm{e}}^{{\rm{j}}2k\left| {r - {r_0}} \right|}} = \frac{2}{{{\pi ^{5/2}}Q\left( k \right){F^2}\left( {\beta ,\gamma } \right)}} \cdot \frac{{{\rho _0}\left( {{\rho _0} - \rho \cos \left( {{\phi _0} - \phi } \right)} \right)}}{{\left| {r - {r_0}} \right|}} \cdot {{\rm{e}}^{{\rm{j}}2k\left| {r - {r_0}} \right|}}$ | (9) |
式(8)的结果即是像函数的表达式,与先前的散射系数$\gamma \left( {\rho ,\phi ,z} \right) = C{k^2}\delta \left( {\rho - {\rho _1}} \right)\delta \left( {\phi - {\phi _1}} \right)\delta \left( {z - {z_1}} \right)$相吻合。以上便是通过某点的散射场推导得到聚焦函数的具体过程。与文献[13]的聚焦函数相比较,除系数不同外,不再涉及位于中心位置上定标体的散射相位${{\rm{e}}^{ - {\rm{j}}k{\rho _0}}}$,所以其通用性较强。聚焦函数得到后,式(2)即是柱面扫描3维近场成像的理论公式。被测目标的3维像分布即等效散射中心分布得到后,通过等效散射点的叠加获得远场散射场,再根据RCS的定义可得其表达式如下:
| $\sigma \left( {k,\theta ,\phi } \right) = \mathop {\lim }\limits_{{r_0} \to \infty } 4\pi r_0^2{\left| {\frac{{{{\mathbf{E}}_{sc}}}}{{{{\mathbf{E}}_i}}}} \right|^2} = \\{k^4}{\left| {\iiint\limits_\Omega {\psi \left( {x,y,z} \right){{\text{e}}^{{\text{j}}2k\left( {x\sin \theta \cos \phi + y\sin \theta \sin \phi + z\cos \theta } \right)}}} {\text{d}}x{\text{d}}y{\text{d}}z} \right|^2}$ |
| (10) |
其中θ表示散射方向矢量与正z轴的夹角,$\phi $表示散射方向矢量在xoy平面的投影矢量与正x轴的夹角。
实际测试中为了消除测量系统参数的影响,得到被测体的真实RCS还需要进行校准这一步骤,选择合适的定标体,重复测量过程,再次获得定标体的像函数${\psi _{cal}}\left( {x,y,z} \right)$,校准公式如下:
| $\sigma '\left( {k,\theta ,\phi } \right) = \frac{{{{\left| {\iiint\limits_\Omega {\psi \left( {x,y,z} \right)}{{\text{e}}^{{\text{j}}2k\left( {x\sin \theta \cos \phi + y\sin \theta \sin \phi + z\cos \theta } \right)}}{\text{d}}x{\text{d}}y{\text{d}}z} \right|}^2}}}{{{{\left| {\iiint\limits_\Omega {{\psi _{cal}}\left( {x,y,z} \right)}{{\text{e}}^{{\text{j}}2k\left( {x\sin \theta \cos \phi + y\sin \theta \sin \phi + z\cos \theta } \right)}}{\text{d}}x{\text{d}}y{\text{d}}z} \right|}^2}}} \cdot {\sigma _{cal}}\left( {k,\theta ,\phi } \right)$ | (11) |
在柱面扫描中,由于式(1)的相位变化相对于幅度变化是快变的,所以为了满足奈奎斯特抽样间隔要求,需要用从相位中提取的最高“频率”(即对相应变量求导数)对应的半“周期”来进行离散采样。经简单推导后,采样间隔如下:
| $\Delta \phi \le \frac{{\pi \sqrt {\rho _{\max }^2 + \rho _0^2} }}{{2{k_{\max }}{\rho _{\max }}{\rho _0}}}, \Delta z \le \frac{{\pi \sqrt {{{\left( {{\rho _0} - {\rho _{\max }}} \right)}^2} + {{\left( {{z_{0\max }} + {z_{\max }}} \right)}^2}} }}{{2{k_{\max }}\left( {{z_{0\max }} + {z_{\max }}} \right)}}, \Delta k \le \frac{\pi }{{2\sqrt {{{\left( {{\rho _0} + {\rho _{\max }}} \right)}^2} + {{\left( {{z_{0\max }} + {z_{\max }}} \right)}^2}} }}$ | (12) |
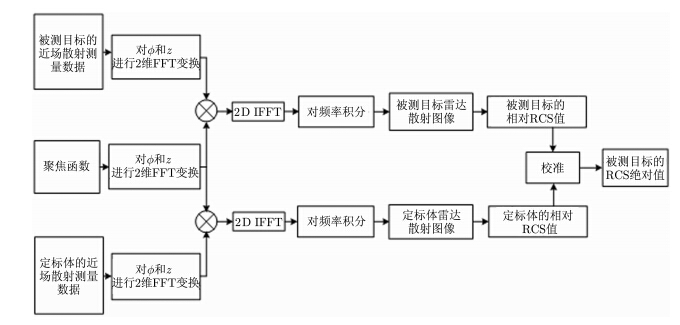
以上是新方法的测量原理,具体的处理流程图如图 2所示。
|
图 2 新方法的处理流程图 Fig.2 Flow chart of the newmethod |
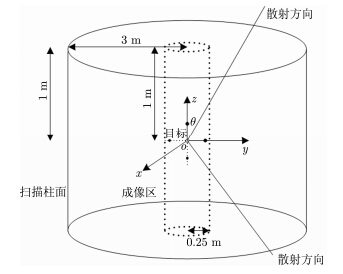
在仿真中,可假设$Q\left( k \right) = 1$以及收发天线是全向的,即$F\left( {\beta ,\gamma } \right) = 1$。被测目标是由yoz平面上4个直径分别为2.50 mm, 1.98 mm, 2.50 mm, 1.98 mm的金属球组成,它们的坐标分别为(0, 0.20 m, 0), (0, -0.20 m, 0), (0, 0, 0.20 m)以及(0, 0, -0.20 m)。定标体是直径为2.50 mm的金属球,其坐标是(0, 0, 0)。成像区域:$0 \le \rho \le 0.25m,0 \le \phi \le 2\pi , - 1 \le z \le 1m$;扫描区域:${\rho _0} = 3$m,$0 \le {\phi _0} \le 2\pi , - 1 \le {z_0} \le 1$m;扫描间隔:$\Delta \phi = 0.001745,\Delta z = 0.01m,\Delta k = 0.2094$;扫描频率范围是8~12 GHz。成像区、扫描区以及被测目标等的坐标示意图如图 3所示。
|
图 3 相关区域以及被测目标等的坐标示意图 Fig.3 Sketch map ofcoordinate system of the related area and target |
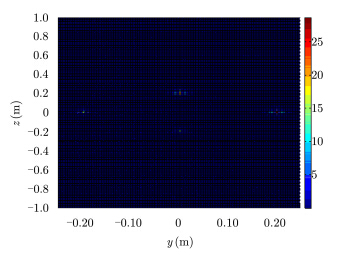
雷达散射图像是获得目标RCS值的中间参量,本文的侧重点在于目标的RCS值而非散射图像,所以在此仅给出目标在yoz平面的散射图像相对分布图(非绝对分布图,这并不影响后面的RCS值,因为还有定标体校准这一步骤),如图 4所示。
|
图 4 目标雷达散射图像相对分布图 Fig.4 Radar relativereflectivity map of the target |
图 4中颜色代表散射图像的强弱分布。图中4个散射点的位置与4个金属球的位置完全一致,上下两点以及右左两点的散射系数峰值比值分别为2.002和2.014,两者很接近2,与实际情况相吻合。之所以有稍微差别主要是因为柱面扫描截断造成的。雷达散射图像得到后,即可获得目标的远场RCS值。为了便于同仿真结果做对照,4个金属球的RCS理论值(忽略多次散射)计算式近似如下:
| $\begin{array}{l} \sigma \left( {\theta ,\phi } \right) = {k^4}\left| {C{{\rm{e}}^{2{\rm{j}}k0.2\sin \theta \sin \phi }} + \frac{1}{2}C{{\rm{e}}^{2{\rm{j}}k - 0.2\sin \theta \sin \phi }}} \right.\\ {\left. { + C{{\rm{e}}^{2{\rm{j}}k0.2\cos \theta }} + \frac{1}{2}C{{\rm{e}}^{2{\rm{j}}k - 0.2\cos \theta }}} \right|^2} \end{array}$ | (13) |
以3dB为误差容限,如果仿真值与理论值的差值超出3 dB,则仿真结果不可信,图 5中每个角度下均可给出两者的差值,故可信域如图 5中虚线所示。在两虚线之间的可信角域内,两组数据吻合较好,除个别角度外,两者差值都在2 dB以内,说明新方法是可行的。可信角域( $75^\circ \le \theta \le 105^\circ $)比柱面所包括的最大角域($71.4^\circ \le \theta \le 108.6^\circ $)稍小。
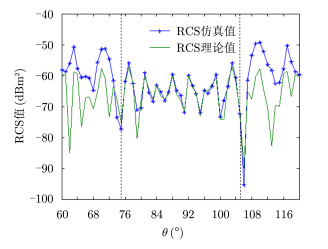
|
图 5 RCS理论值与仿真值 Fig.5 RCS theoretical results and simulated results |
为了分析柱面扫描高度对RCS结果的影响,设置扫描高度为2.0 m, 2.5 m以及3.0 m进行仿真,高度扫描间隔$\Delta z$不变,保持为0.01 m,利用新方法得到的RCS仿真值以及理论值如图 6所示。
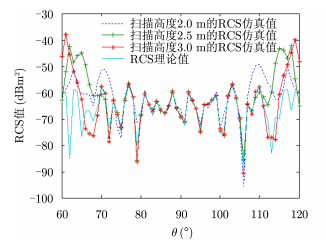
|
图 6 RCS理论值与不同扫描高度下的RCS仿真值 Fig.6 RCS theoretical results and simulated results of different scanning height |
随扫描高度的增加,RCS结果的可信度以及可信域逐渐增加。因此为了减少柱面截断误差,增加可信角域,柱面扫描高度应尽量大。
4 结束语本论文提出一种基于柱面扫描成像的RCS测量新方法,它是由圆迹2维成像方法扩展而来,仿真结果证实了该方法的可靠性和正确性,具体应用中,应尽可能地选择柱面高度较大的扫描面,这样便可减少扫描面截断误差,进而得到更好的RCS结果。本文所提模型中没有对被测物的位置加以限制,且能得到3维立体角域的RCS值,因而具有更强的实用性。受限于试验条件,目前通过仿真给出了针对相应散射目标的可信角域,后续工作中需对可信角域进行深入的分析并给出其具体的经验计算公式,以方便实际测试中发挥新方法的潜在工程应用价值。
| [1] |
吴鹏飞, 许小剑. 地面平面场RCS测量异地定标误差分析[J]. 雷达学报, 2012, 1(1): 58-62. Wu Peng-fei and XuXiao-jian. Error analysis of relative calibration for RCS measurement on groundplane range[J]. Journal of Radars, 2012, 1(1): 58-62. (  1) 1)
|
| [2] |
Amin F, MueedA, and Xu Jia-dong. Implementation and results of an RCS measurement system inCATR[C]. IEEE Asia-Pacific Conference on Applied Electromagnetics, Melaka, Malaysia, 2012: 262-267.
( 1) 1)
|
| [3] |
Yu Jun-sheng,Liu Xiao-ming, and Yao Yuan. The design and manufacture of a high frequencyCATR[C]. Millimeter Waves and THz Technology Workshop, Rome, 2013: 1-2.
( 1) 1)
|
| [4] |
Ford K L,Bennett J C, and Holtby D G. Use of a plane-wave synthesis technique to obtaintarget RCS from near-field measurements with selective feature extractioncapability[J]. IEEE Transactions on Antennas and Propagation, 2013,61(4): 2051-2057.
( 1) 1)
|
| [5] |
Qureshi M A,Schmidt C H, and Eibert T F. Efficient near-field far-filed transformation fornonredundant sampling representation on arbitrary surfaces in near-filedantenna measurements[J]. IEEE Transactions on Antennas and Propagation,2013, 61(4): 2025-2033.
( 1) 1)
|
| [6] |
Gao Chao, YuanXiao-feng, and Bai Yang. An approach for extrapolating far field radarcross-section from near field measurement[C]. IEEE International Conference onGreen Computing and Communications, Beijing, 2013: 1604-1607.
( 1) 1)
|
| [7] |
Cown B J andRyan C E. Near-field scattering measurements for determining complex targetRCS[J]. IEEE Transactions on Antennas and Propagation, 1989, 37(5): 576-585.
( 1) 1)
|
| [8] |
Odendaal J Wand Joubert J. Radar cross measurements using near-field imaging[J]. IEEETransactions on Instrument Measurement, 1996, 45(6): 948-954.
( 1) 1)
|
| [9] |
Broquetas A, Palau J, Jofre L, et al.. Spherical wave near-field imaging and radar cross-sectionmeasurement[J]. IEEE Transactions on Antennas and Propagation, 1998,46(5): 730-735.
( 1) 1)
|
| [10] |
Vaupel T andEibert T F. Comparison and application of near-field isar imaging techniquesfor far-field radar cross section determination[J]. IEEE Transactions onAntennas and Propagation, 2006, 54(1): 144-151.
( 2) 2)
|
| [11] |
Nicholson K Jand Wang C H. Improved near-field radar cross-section measurement technique[J].IEEE Antennas and Wireless Propagation Letters, 2009, 8: 1103-1106.
( 1) 1)
|
| [12] |
Li S, Zhu B,Sun H, et al.. NUFFT-Based near-field imaging technique for far-fieldradar cross section calculation[J]. IEEE Antennas and Wireless PropagationLetters, 2010, 9: 550-553.
( 1) 1)
|
| [13] |
Kobayashi H,Osipov A, Suzuki H, et al.. An improved image- basednear-field-to-far-field transformation for cylindrical scanningsurfaces[C]. General Assembly and Scientific Symposium, Istanbul, Turkey, 2011: 1-4.
( 6) 6)
|
| [14] |
Osipov A,Kobayashi H, Suzuki H, et al.. An improved imaged-based circularnear-field-to-far-field transformation[J]. IEEE Transactions on Antennas andPropagation, 2013, 61(2): 989-993.
( 2) 2)
|


