② 63612部队 瓜州 736100
② PLA, No. 63612 Troop, Guazhou 736100, China
电子干扰与抗干扰技术的发展给制导武器带来了前所未有的巨大挑战。微型空射雷达诱饵作为一种新型角度欺骗干扰手段,通过与真实目标协同伴飞且逼真模拟目标相关特性,干扰和破坏雷达系统对目标的搜索跟踪,通过充当“清道夫”,以“自我牺牲”的方式吸引制导雷达攻击,实现了真正意义上的载体外(off-board)干扰,达到了减小制导武器杀伤力,提高目标生存能力的目的[1]。
空射诱饵干扰通过模拟目标飞行包线以及雷达回波特性,缩小诱饵与目标之间的特征差异来形成波束内的不可分辨多目标,达到吸引波束照射,扰乱参数测量,诱骗雷达跟踪的目的。由于目标与诱饵之间特征差异小,二者回波相互干涉混叠,引起观测不确定性,导致单脉冲测量存在较大偏差[2]。干扰条件下,常规先对目标和诱饵进行信号分离与观测提取,再进行参数测量与状态估计的跟踪方法只能获取干扰或者目标与干扰能量质心的状态信息,无法准确估计真实目标状态实现稳定跟踪。
针对波束内多个目标的检测跟踪问题,Nandakumaran等人[3]提出了在理想采样模型下利用跟踪信息实现对两个以上目标进行联合检测和跟踪的方法,并通过将目标状态转化为检测参数,使得联合检测与跟踪处理能够适应目标数目未知、变化等复杂场景。该方法侧重于实时判决和估计目标的个数及其对应状态,需要判断目标新生及死亡状态,以实现稳定检测和跟踪。Hue等人[4]对基于粒子滤波进行多目标跟踪的问题进行了深入研究,获得了粒子多目标跟踪的基本流程。在末制导有源雷达诱饵干扰情况下,由于雷达接收回波的观测混叠以及目标和诱饵身份的不确定性,制导雷达要实现对波束内真实目标的选择和跟踪,完成正确的引导攻击,首先必须在目标逃离波束之前保持对波束内目标和诱饵的同时跟踪,并且持续获取目标和诱饵二者的跟踪状态和航迹信息,以此为处理系统利用跟踪状态、航迹以及其他信息实现对目标和诱饵的身份辨识以及分选,进而调整波束指向实现稳定跟踪提供条件。本文结合末制导有源诱饵干扰场景,在详细分析干扰原理及特性的基础上,推导了雷达波束内不可分辨多目标非理想信号模型,基于干扰条件下回波观测及其似然函数特征,采用粒子滤波多目标跟踪方法,绕开观测提取、参数测量以及数据关联等过程,直接对雷达接收机和差通道数据进行处理,利用粒子在状态空间中的传播和递推近似目标与诱饵的联合状态条件概率密度,实现了波束内不可分辨目标与诱饵的联合跟踪。
2 问题描述与建模 2.1 干扰原理及样式空射诱饵的干扰本质是通过信号模拟与协同伴飞使得目标和诱饵不可分辨,形成雷达波束内的非相干两点源,以足够的保真度激励、误导和诱骗跟踪雷达天线电轴偏离目标而指向诱饵,造成失跟或误跟,最终导致脱靶。设雷达回波中诱饵干扰功率与目标回波功率之比为K (通常称之为干扰压制比),则雷达天线电轴指向相对于目标与诱饵几何中心线的偏角θ为[5]:
| $\theta = \frac{{\Delta \theta }}{2}\frac{{{K^2} - 1}}{{{K^2} + 1}}$ | (1) |
空射式诱饵干扰通过与真实目标协同伴飞的方式实现干扰欺骗,其干扰过程可简单描述为:目标遭受制导攻击时向侧方或侧前方空射出微型雷达诱饵,诱饵截获制导雷达信号,采用复合调制模拟后进行转发。在释放初期,由于目标诱饵间距小,且干扰信号功率大,极易捕获雷达跟踪波门。诱饵通过协同伴飞模拟目标飞行包线和运动特征,误导雷达将诱饵当作真实目标进行测量跟踪,使波束中心指向逐渐偏向诱饵。随着目标与诱饵相对于制导雷达张角的不断增大,目标逐渐向波束边沿移动,最终逃离波束,导致雷达丢失目标,跟踪和命中无价值的诱饵。
目标和诱饵在制导雷达波束内协同运动,三者之间的相对运动剧烈,位置关系动态变化。设k时刻制导雷达处于球坐标系的原点位置, $\left( {{\theta _{{\rm{a}},k}},{\theta _{{\rm{e}},k}}} \right)$为当前时刻天线电轴指向的方位和俯仰。目标与诱饵相对雷达的径向距离、方位以及俯仰角构成当前位置坐标$P_k^j = {\left( {\rho _k^j,\varsigma _{{\rm{a}},k}^j,\varsigma _{{\rm{e}},k}^j} \right)^{\rm{T}}}\left( {j = {\rm{T}},{\rm{D}}} \right)$,其中T表示目标,D表示诱饵。上述极坐标系下的位置 $P_k^j$可以转化为跟踪滤波中笛卡尔坐标系下的位置$X_k^j = {\left( {x_k^j,y_k^j,z_k^j} \right)^{\rm{T}}}$,反之亦然。两个坐标系下位置坐标的相互转换关系如式(2)和式(3)所示[6]。
| $\left. \begin{array}{l} x_k^j = \rho _k^j\cos \left( {\varsigma _{{\rm{e}},k}^j} \right)\cos \left( {\varsigma _{{\rm{a}},k}^j} \right)\\ y_k^j = \rho _k^j\cos \left( {\varsigma _{{\rm{e}},k}^j} \right)\sin \left( {\varsigma _{{\rm{a}},k}^j} \right)\\ z_k^j = \rho _k^j\sin \left( {\varsigma _{{\rm{e}},k}^j} \right) \end{array} \right\}$ | (2) |
| $\left. \begin{array}{l} \varsigma _{{\rm{a}},k}^j = \arctan \left( {\frac{{y_k^j}}{{x_k^j}}} \right)\\ \varsigma _{{\rm{e}},k}^j = \arctan \left( {\frac{{z_k^j}}{{\rho _k^j}}} \right)\\ \rho _k^j = \sqrt {{{\left( {x_k^j} \right)}^2} + {{\left( {y_k^j} \right)}^2} + {{\left( {z_k^j} \right)}^2}} \end{array} \right\}$ | (3) |
参数测量与估计中,k时刻目标与诱饵对应的参数向量可表示为 $\lambda _k^j = \left( {\alpha _k^j,\eta _{{\rm{a}},k}^j,\eta _{{\rm{e}},k}^j} \right)\left( {j = {\rm{T}},{\rm{D}}} \right)$(其中α为目标的子波门内相对距离, ${\eta _{\rm{a}}}$为方位维归一化电轴角,${\eta _{\rm{e}}}$为俯仰维归一化电轴角)。 $\lambda _k^j$是当前时刻雷达、目标和诱饵之间相对位置关系的具体体现。 $\lambda _k^j$可以转化为球坐标系下的位置坐标$P_k^j$,反之亦然。二者之间的相互转换关系如式(4)和式(5)所示[7]。
| $\left. \begin{array}{l} \eta _{{\rm{a}},k}^j = \frac{{\left( {\varsigma _{{\rm{a}},k}^j - \theta _{{\rm{a}},k}^{}} \right)}}{{{B_{\rm{a}}}}}\\ \eta _{{\rm{e}},k}^j = \frac{{\left( {\varsigma _{{\rm{e}},k}^j - \theta _{{\rm{e}},k}^{}} \right)}}{{{B_{\rm{e}}}}}\\ \alpha _k^j = \frac{{\bmod \left( {\rho _k^j,{\rm{BW}}} \right)}}{{{\rm{BW}}}} \end{array} \right\}$ | (4) |
| $\left. \begin{array}{l} \varsigma _{{\rm{a}},k}^j = {\theta _{{\rm{a}},k}} + \left( {\eta _{{\rm{a}},k}^j{B_{\rm{a}}}} \right)\\ \varsigma _{{\rm{e}},k}^j = {\theta _{{\rm{e}},k}} + \left( {\eta _{{\rm{e}},k}^j{B_{\rm{e}}}} \right)\\ \rho _k^j = \left( {{N_k} + \alpha _k^j} \right){\rm{BW}} \end{array} \right\}$ | (5) |
式(2)-式(5)给出了回波观测、测量参数在各个坐标系之间的转换关系,其中k时刻雷达天线电轴指向 $\left( {{\theta _{{\rm{a}},k}},{\theta _{{\rm{e}},k}}} \right)$是根据当前时刻的雷达、目标和诱饵的三角几何关系,以及干扰压制比条件等,根据非相干两点源干扰原理来确定的。这是末制导干扰条件下目标跟踪的显著特点。
2.2 信号模型典型单脉冲雷达系统中,单个目标和差通道接收回波的同相以及正交分量的表达式为[8]:
| $\left. \begin{array}{l} {s_{\rm{i}}} = x + {n_{{\rm{si}}}}, {s_{\rm{q}}} = y + {n_{{\rm{sq}}}}\\ {d_{\rm{a}}}_{\rm{i}} = {\eta _{\rm{a}}}x + {n_{{\rm{dai}}}}, {d_{\rm{a}}}_{\rm{q}} = {\eta _{\rm{a}}}y + {n_{{\rm{daq}}}}\\ {d_{\rm{e}}}_{\rm{i}} = {\eta _{\rm{e}}}x + {n_{{\rm{dei}}}}, {d_{\rm{e}}}_{\rm{q}} = {\eta _{\rm{e}}}y + {n_{{\rm{deq}}}} \end{array} \right\}$ | (6) |
其中 $x = \beta \cos \phi , y = \beta \sin \phi , {\eta _{\rm{a}}}, {\eta _{\rm{e}}}$为方位和俯仰DOA (DirectionOf Arrival), $\beta ,\phi $为幅度和相位。 ${n_{{\rm{si}}}},{n_{{\rm{sq}}}} \sim N\left( {0,\sigma _{\rm{s}}^{\rm{2}}} \right)$为和通道噪声, ${n_{{\rm{dai}}}},{n_{{\rm{daq}}}},{n_{{\rm{dei}}}},{n_{{\rm{deq}}}} \sim N\left( {0,\sigma _{\rm{d}}^{\rm{2}}} \right)$为差通道噪声。假定目标回波和诱饵干扰皆满足SwerlingⅡ模型[8],即β起伏服从脉间瑞利分布,则 $x,y$服从均值为0,方差为 $\sigma _0^2$的高斯分布。
实际中对雷达接收机的匹配滤波输出信号进行采样时,目标回波能量通常会“溢出”到相邻的匹配滤波采样点上,即实际目标的位置一般不会刚好位于某一个采样点上,而大多数情况是位于相邻的某两个或多个采样点之间[9, 10]。相比于通常认为目标位置与采样点位置重合的理想假设,这一模型更加符合实际信号处理过程,且理论上可利用相邻多个匹配滤波采样点包含的信息改善估计精度。不失一般性,设发射信号为矩形脉冲,则匹配滤波后的输出回波为三角形包络。设发射脉冲宽度为T,则三角包络底边宽度为2T。控制采样率为脉冲宽度的倒数1/T,则目标能量只会出现在相邻的两个匹配滤波采样点上。对于波束内不可分辨的目标和诱饵,二者处于跟踪雷达同一分辨单元内,即同时位于两个连续的匹配滤波采样点之间,对应采样信号模型如图 1所示。
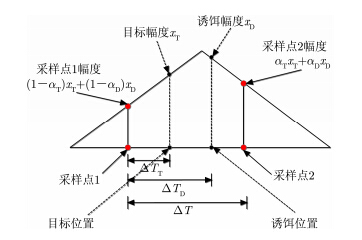 | 图 1 目标和诱饵处于两个连续匹配滤波采样点之间的信号模型Fig. 1 The signal model of unresolved targets |
图 1中 $\Delta {T_{\rm{T}}}$和 $\Delta {T_{\rm{D}}}$分别为目标和诱饵与采样点1之间的时间偏移,表征了二者在脉冲内的相对距离。实际目标和诱饵的真实位置未知,均匀分布在两个连续采样点之间。设目标和诱饵的回波幅度分别为 ${x_{\rm{T}}}$和${x_{\rm{D}}}$,则采样点1幅度为$\left( {1 - \Delta {T_{\rm{T}}}/T} \right) \cdot {x_{\rm{T}}} + \left( {1 - \Delta {T_{\rm{D}}}/T} \right){x_{\rm{D}}}$。令 ${\alpha _{\rm{T}}} = \Delta {T_{\rm{T}}}/T, {\alpha _{\rm{D}}} = \Delta {T_{\rm{D}}}/T$,则采样点1和采样点2的幅度可分别表示为 $\left( {1 - {\alpha _{\rm{T}}}} \right){x_{\rm{T}}} + \left( {1 - {\alpha _{\rm{D}}}} \right){x_{\rm{D}}}$和 ${\alpha _{\rm{T}}}{x_{\rm{T}}} + {\alpha _{\rm{D}}}{x_{\rm{D}}}$。
不可分辨的目标和诱饵处于同一雷达分辨单元中,接收回波由二者共同构成。k时刻,第m个发射脉冲对应的回波观测信号${Z_k}(m)$为:
| $\begin{array}{l} {{\bf{Z}}_k}(m) = \left[ {{s_{i1,k}}(m),{s_{i2,k}}(m),{d_{{\rm{a}}i1,k}}(m),} \right.\\ {\rm{ }}{\left. {{d_{{\rm{a}}i2,k}}(m),{d_{{\rm{e}}i1,k}}(m),{d_{{\rm{e}}i2,k}}(m)} \right]^{\rm{T}}} \end{array}$ | (7) |
| $\left. \begin{array}{l} {s_{i1,k}}(m) = \left( {1 - \alpha _{\rm{T}}^k} \right){x_{\rm{T}}}(m) + \left( {1 - \alpha _{\rm{D}}^k} \right){x_{\rm{D}}}(m) + n_{{\rm{s}}i1}^k(m)\\ {s_{i2,k}}(m) = \alpha _{\rm{T}}^k{x_{\rm{T}}}(m) + \alpha _{\rm{D}}^k{x_{\rm{D}}}(m) + n_{{\rm{s}}i2}^k(m)\\ {d_{{\rm{a}}i1,k}}(m) = \left( {1 - \alpha _{\rm{T}}^k} \right)\eta _{{\rm{aT}}}^k{x_{\rm{T}}}(m)\\ + \left( {1 - \alpha _{\rm{D}}^k} \right)\eta _{{\rm{aD}}}^k{x_{\rm{D}}}(m) + n_{{\rm{dai}}1}^k(m)\\ {d_{{\rm{a}}i2,k}}(m) = \alpha _{\rm{T}}^k\eta _{{\rm{aT}}}^k{x_{\rm{T}}}(m) + \alpha _{\rm{D}}^k\eta _{{\rm{aD}}}^k{x_{\rm{D}}}(m) + n_{{\rm{dai}}2}^k(m)\\ {d_{{\rm{e}}i1,k}}(m) = \left( {1 - \alpha _{\rm{T}}^k} \right)\eta _{{\rm{eT}}}^k{x_{\rm{T}}}(m)\\ + \left( {1 - \alpha _{\rm{D}}^k} \right)\eta _{{\rm{eD}}}^k{x_{\rm{D}}}(m) + n_{{\rm{dei}}1}^k(m)\\ {d_{{\rm{e}}i2,k}}(m) = \alpha _{\rm{T}}^k\eta _{{\rm{eT}}}^k{x_{\rm{T}}}(m) + \alpha _{\rm{D}}^k\eta _{{\rm{eD}}}^k{x_{\rm{D}}}(m) + n_{{\rm{dei}}2}^k(m) \end{array} \right\}$ | (8) |
| $\lambda _k^J = \left[ {\lambda _{\rm{T}}^k,{\rm{ }}\lambda _{\rm{D}}^k} \right]$ | (9) |
根据目标和诱饵的SwerlingⅡ模型假定,当雷达连续发射M个独立脉冲时,在给定参数向量$\lambda _k^J$条件下,观测向量${{\bf{Z}}_k}(m)$服从零均值高斯分布,其条件似然函数可表示为[2]:
| $\begin{array}{l} L\left( {\lambda _k^J} \right) = p\left( {{{\bf{Z}}_k}|\lambda _k^J} \right)\\ {\rm{ = }}\prod\limits_{m{\rm{ = 1}}}^M {\left( {\frac{1}{{|2\pi {{\bf{R}}_k}{|^{1/2}}}}\exp \left( { - \frac{1}{2}{{\bf{Z}}_k}{{(m)}^{\rm{T}}}{\bf{R}}_k^{ - {\rm{1}}}{Z_k}(m)} \right)} \right)} \end{array}$ | (10) |
| $\begin{array}{l} {{\bf{R}}_k} = {\rm{E}}\left[ {{{\bf{Z}}_k}(m){{\bf{Z}}_k}{{(m)}^{\rm{T}}}} \right]\\ = \sum\limits_{j = 1}^N {\left[ {\begin{array}{*{20}{c}} {\sigma _{0,j}^2{{\left( {\gamma _k^j} \right)}^2}}&{\sigma _{0,j}^2\gamma _k^j\alpha _k^j}&{\sigma _{0,j}^2{{\left( {\gamma _k^j} \right)}^2}\eta _{{\rm{a}},k}^j}&{\sigma _{0,j}^2\gamma _k^j\alpha _k^j\eta _{{\rm{a}},k}^j}&{\sigma _{0,j}^2{{\left( {\gamma _k^j} \right)}^2}\eta _{{\rm{e}},k}^j}&{\sigma _{0,j}^2\gamma _k^j\alpha _k^j\eta _{{\rm{e}},k}^j}\\ {}&{\sigma _{0,j}^2{{\left( {\alpha _k^j} \right)}^2}}&{\sigma _{0,j}^2\gamma _k^j\alpha _k^j\eta _{{\rm{a}},k}^j}&{\sigma _{0,j}^2{{\left( {\alpha _k^j} \right)}^2}\eta _{{\rm{a}},k}^j}&{\sigma _{0,j}^2\gamma _k^j\alpha _k^j\eta _{{\rm{e}},k}^j}&{\sigma _{0,j}^2{{\left( {\alpha _k^j} \right)}^2}\eta _{{\rm{e}},k}^j}\\ {}&{}&{\sigma _{0,j}^2{{\left( {\gamma _k^j} \right)}^2}{{\left( {\eta _{{\rm{a}},k}^j} \right)}^2}}&{\sigma _{0,j}^2\gamma _k^j\alpha _k^j{{\left( {\eta _{{\rm{a}},k}^j} \right)}^2}}&{\sigma _{0,j}^2{{\left( {\gamma _k^j} \right)}^2}\eta _{{\rm{a}},k}^j\eta _{{\rm{e}},k}^j}&{\sigma _{0,j}^2\gamma _k^j\alpha _k^j\eta _{{\rm{a}},k}^j\eta _{{\rm{e}},k}^j}\\ {}&{}&{}&{\sigma _{0,j}^2{{\left( {\alpha _k^j} \right)}^2}{{\left( {\eta _{{\rm{a}},k}^j} \right)}^2}}&{\sigma _{0,j}^2\gamma _k^j\alpha _k^j\eta _{{\rm{a}},k}^j\eta _{{\rm{e}},k}^j}&{\sigma _{0,j}^2{{\left( {\alpha _k^j} \right)}^2}\eta _{{\rm{a}},k}^j\eta _{{\rm{e}},k}^j}\\ {}&{}&{}&{}&{\sigma _{0,j}^2{{\left( {\gamma _k^j} \right)}^2}{{\left( {\eta _{{\rm{e}},k}^j} \right)}^2}}&{\sigma _{0,j}^2\gamma _k^j\alpha _k^j{{\left( {\eta _{{\rm{e}},k}^j} \right)}^2}}\\ {}&{}&{}&{}&{}&{\sigma _{0,j}^2{{\left( {\alpha _k^j} \right)}^2}{{\left( {\eta _{{\rm{e}},k}^j} \right)}^2}} \end{array}} \right]} \\ + {\rm{diag}}(\sigma _{\rm{s}}^{\rm{2}},\sigma _{\rm{s}}^{\rm{2}},\sigma _{\rm{d}}^{\rm{2}},\sigma _{\rm{d}}^{\rm{2}},\sigma _{\rm{d}}^{\rm{2}},\sigma _{\rm{d}}^{\rm{2}}), N{\rm{ = 1,2}} \end{array}$ |
| (11) |
信噪比可定义为式(12)所示,其中M为积累脉冲数,${\left( {{\sigma ^j}} \right)^2}$为目标(或诱饵)的回波功率。
| ${\rm{SNR}} = 10\lg \left( {\frac{M}{{\sigma _{\rm{s}}^{\rm{2}}}}\sum\limits_{j = 1}^2 {{{\left( {{\sigma ^j}} \right)}^2}} } \right)$ | (12) |
目标与诱饵的不可分辨导致回波干涉混叠,基于混合观测进行测量估计只能获得目诱能量质心对应的参数及状态,而目标和诱饵各自独立的测量无法获得,导致雷达系统无法实现对波束内真实目标准确的观测提取、参数测量和状态估计。式(7),式(8)和式(11)的回波观测模型以及式(2)-式(5)的转换关系所表征的观测模型的非线性、复杂系统的非高斯性以及噪声协方差阵的未知性使得状态估计问题的求解更为不易。粒子滤波[11, 12]作为一种非线性滤波器,能够适应干扰条件下观测模型的非线性以及噪声协方差的未知性。基于干扰存在性检测信息[13],在回波混叠和观测不确定条件下可以通过粒子在状态空间中的传播递推来近似目标和诱饵状态的联合条件概率密度,从而能够绕过观测提取和参数测量过程,直接对雷达接收的和差通道数据进行处理,构建对应的状态回归。
设J表示波束内的目标个数,J表示检测到波束内同时存在目标和诱饵,为简化分析,此处假定检测无漏检和虚警。${\bf{X}}_k^J = \left[ {\begin{array}{*{20}{c}} {{\bf{X}}_k^1}&{{\bf{X}}_k^2} \end{array}} \right]$为k时刻目标与诱饵的联合状态向量, ${{\bf{Z}}_k}$为观测向量,构成如式(7)。根据式(10)的观测条件似然$p\left( {{{\bf{Z}}_k}|\lambda _k^J} \right)$,如果能够从联合状态向量的后验分布$p\left( {\left. {{\bf{X}}_{k - 1}^J} \right|} \right.\left. {{{\bf{Z}}_{k - 1}}} \right) = p\left( {{\bf{X}}_{k - 1}^J|{{\left\{ {{Z_l}} \right\}}_{l \le \left( {k - 1} \right)}}} \right)$中抽取I个独立同分布的状态样本 $\left\{ {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}, i = 1,2, \cdots ,I} \right\}$,则目标和诱饵联合状态向量的后验概率密度分布可以逼近为[14]:
| $p\left( {{\bf{X}}_{k - 1}^J|{{\bf{Z}}_{k - 1}}} \right) = \frac{1}{I}\sum\limits_{i = 1}^I {\delta \left( {{\bf{X}}_{k - 1}^J - {{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right)} $ | (13) |
考虑到直接从状态概率函数中采样的困难,可从相对容易采样的重要性分布函数 $q\left( {{\bf{X}}_{k - 1}^J|{{\bf{Z}}_{k - 1}}} \right)$中独立抽取I个状态样本 $\left\{ {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}, i = 1,2, \cdots ,I} \right\}$,以近似联合状态向量的后验分布[15]:
| $\left. \begin{array}{l} p\left( {{\bf{X}}_{k - 1}^J|{{\bf{Z}}_{k - 1}}} \right) \simeq \sum\limits_{i = 1}^I {{{\left[ {w_{k - 1}^J} \right]}_i}\delta \left( {{\bf{X}}_{k - 1}^J - {{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right)} \\ {\left[ {w_{k - 1}^J} \right]_i} = \widetilde w_{k - 1}^J/\sum\limits_{i = 1}^I {\widetilde w_{k - 1}^J} \end{array} \right\}$ | (14) |
${\left[ {\widetilde w_{k - 1}^J} \right]_i} = \frac{{p\left( {{{\bf{Z}}_{k - 1}}\left| {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right.} \right)p\left( {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right)}}{{q\left( {\left. {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right|{{\bf{Z}}_{k - 1}}} \right)}}$
在获得k-1时刻联合状态向量 ${\bf{X}}_{k - 1}^J$后验概率密度分布的近似估计后,基于k时刻的观测${Z_k}$,利用贝叶斯原理可得k时刻目标和诱饵联合状态向量的后验密度分布为:
| $\begin{array}{l} p\left( {{\bf{X}}_k^J|{{\bf{Z}}_k}} \right)\\ = \frac{{p\left( {{\bf{X}}_k^J,{{\bf{Z}}_k}|{{\bf{Z}}_{k - 1}}} \right)}}{{p\left( {{{\bf{Z}}_k}|{{\bf{Z}}_{k - 1}}} \right)}} = \frac{{p\left( {{{\bf{Z}}_k}|{\bf{X}}_k^J,{{\bf{Z}}_{k - 1}}} \right)p\left( {{\bf{X}}_k^J|{{\bf{Z}}_{k - 1}}} \right)}}{{p\left( {{{\bf{Z}}_k}|{{\bf{Z}}_{k - 1}}} \right)}}\\ {\rm{ = }}\frac{{p\left( {{{\bf{Z}}_k}|{\bf{X}}_k^J,{{\bf{Z}}_{k - 1}}} \right)p\left( {{\bf{X}}_k^J|{\bf{X}}_{k - 1}^J,{{\bf{Z}}_{k - 1}}} \right)p\left( {{\bf{X}}_{k - 1}^J|{{\bf{Z}}_{k - 1}}} \right)}}{{p\left( {{{\bf{Z}}_k}|{{\bf{Z}}_{k - 1}}} \right)}}\\ {\rm{ = }}\frac{{p\left( {{{\bf{Z}}_k}|{\bf{X}}_k^J} \right)p\left( {{\bf{X}}_k^J|{\bf{X}}_{k - 1}^J} \right)}}{{p\left( {{{\bf{Z}}_k}|{{\bf{Z}}_{k - 1}}} \right)}}p\left( {{\bf{X}}_{k - 1}^J|{{\bf{Z}}_{k - 1}}} \right) \end{array}$ | (15) |
则k时刻的重要性分布函数可以表示为:
| $q\left( {{\bf{X}}_k^J|{{\bf{Z}}_k}} \right) \buildrel \Delta \over = q\left( {{\bf{X}}_k^J|{\bf{X}}_{k - 1}^J,{{\bf{Z}}_k}} \right)q\left( {{\bf{X}}_{k - 1}^J|{{\bf{Z}}_{k - 1}}} \right)$ | (16) |
将式(15),式(16)代入式(14)可得归一化重要性权的迭代公式
| $\begin{array}{l} {\left[ {w_k^J} \right]_i} \propto \frac{{p\left( {{{\bf{Z}}_k}\left| {{{\left[ {{\bf{X}}_k^J} \right]}_i}} \right.} \right)p\left( {{{\left[ {{\bf{X}}_k^J} \right]}_i}\left| {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right.} \right)p\left( {\left. {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right|{{\bf{Z}}_{k - 1}}} \right)}}{{q\left( {{{\left[ {{\bf{X}}_k^J} \right]}_i}\left| {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right.,{{\bf{Z}}_k}} \right)q\left( {\left. {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right|{{\bf{Z}}_{k - 1}}} \right)}}\\ {\rm{ = }}{\left[ {w_{k - 1}^J} \right]_i}\frac{{p\left( {{{\bf{Z}}_k}\left| {{{\left[ {{\bf{X}}_k^J} \right]}_i}} \right.} \right)p\left( {{{\left[ {{\bf{X}}_k^J} \right]}_i}\left| {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right.} \right)}}{{q\left( {{{\left[ {{\bf{X}}_k^J} \right]}_i}\left| {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right.,{{\bf{Z}}_k}} \right)}}\\ {\rm{ = }}{\left[ {w_{k - 1}^J} \right]_i}\frac{{p\left( {{{\bf{Z}}_k}\left| {{{\left[ {{\bf{X}}_k^J} \right]}_i}} \right.} \right)p\left( {{{\left[ {{\bf{X}}_k^J} \right]}_i}\left| {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right.} \right)}}{{q\left( {{{\left[ {{\bf{X}}_k^J} \right]}_i}\left| {{{\left[ {{\bf{X}}_{k - 1}^J} \right]}_i}} \right.,{{\bf{Z}}_k}} \right)}} \end{array}$ | (17) |
由此可得迭代更新后目标和诱饵的联合条件状态后验概率分布为:
| $p\left( {{\bf{X}}_k^J|{{\bf{Z}}_k}} \right) \simeq \sum\limits_{i = 1}^I {{{\left[ {w_k^J} \right]}_i}\delta \left( {{\bf{X}}_k^J - {{\left[ {{\bf{X}}_k^J} \right]}_i}} \right)} $ | (18) |
当样本数 $I \to \infty $时,式(18)趋近于真实的目标和诱饵联合状态后验分布$p\left( {{\bf{X}}_k^J|{{\bf{Z}}_k}} \right)$,在此基础上可求解获得状态的均值、协方差等各种统计信息用于跟踪滤波。
4 目标与诱饵联合跟踪滤波目标和诱饵的不可分辨使得雷达对其波束内单个个体的信号分离、观测提取和参数测量过程无法准确实现。在正确检测到波束内存在干扰的情况下,基于非理想采样条件下的不可分辨信号模型,采用粒子滤波多目标跟踪方法,利用粒子在状态空间的迭代可直接从混叠的观测中获得目标和诱饵联合状态向量的条件后验分布,进而获取二者的联合状态向量,实现目标与诱饵的联合跟踪。设干扰过程中,目标和诱饵的运动所对应的状态方程和观测方程可表示为[16]:
| ${s^j}\left( {k + 1} \right) = F{s^j}\left( k \right) + {v^j}\left( k \right)$ | (19) |
| ${r^j}\left( k \right) = H{s^j}\left( k \right) + {w^j}\left( k \right)$ | (20) |
其中F和H分别为状态转移矩阵和输入输出矩阵,${s^j}\left( k \right)$为k时刻目标j的6维状态向量,前3维表示目标的位置坐标,后3维表示对应的速度。${v^j}\left( k \right)$和${w^j}\left( k \right)$分别为处理噪声和观测噪声,二者均值为零,对应的协方差为${\rm{E}}\left( {{v^j}\left( k \right){v^j}{{\left( k \right)}^{\rm{T}}}} \right) = Q,{\rm{E}}\left( {{w^j}\left( k \right){w^j}{{\left( k \right)}^{\rm{T}}}} \right) = R$,并且目标和诱饵之间不相关。
当制导雷达检测到干扰发生后,基于式(7),式(8)的回波观测以及式(19),式(20)的状态和观测方程,采用式(15)-式(18)的联合状态后验估计直接对雷达接收机的和、差通道回波信号进行处理,绕开观测提取、参数测量、数据关联等多个过程,获取联合状态向量条件后验分布,实现波束内目标和诱饵的联合跟踪。联合跟踪处理分为5个主要处理阶段,如图 2所示。
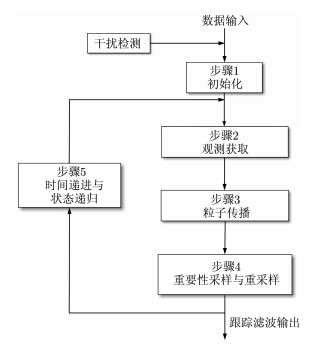 | 图 2 不可分辨目标与诱饵联合跟踪处理流程Fig. 2 The joint tracking process of unresolved targets |
上述联合跟踪处理流程中,对应5个阶段的信号及数据处理步骤为:
步骤1 初始化
(1) 定义I为处理过程使用的粒子总数,对于 $i = 1,2, \cdots ,I$和j=1,2(分别为目标和诱饵),令目标和诱饵的初始参数粒子服从对应的均匀分布,即 ${\left[ {\alpha _0^j} \right]_i} \sim {\rm{U}}\left( {0,1} \right), {\left[ {\eta _{{\rm{a}},0}^j} \right]_i} \sim {\rm{U}}\left( { - 1,1} \right)$和 ${\left[ {\eta _{{\rm{e}},0}^j} \right]_i} \sim {\rm{U}}\left( { - 1,1} \right)$;
(2) 初始化参数粒子经式(2)-式(5)转换为直角坐标系下目标和诱饵的初始联合位置坐标粒子 ${\left[ {{\chi _0}} \right]_i} = {\left[ {\begin{array}{*{20}{c}} {\left[ {\chi _0^1} \right]_i^{\rm{T}}}&{\left[ {\chi _0^2} \right]_i^{\rm{T}}} \end{array}} \right]^{\rm{T}}}$,其中 $\left[ {\chi _0^1} \right]_i^{\rm{T}}$和 $\left[ {\chi _0^2} \right]_i^{\rm{T}}$分别表示目标和诱饵各自的初始化位置坐标粒子,同时设制导雷达的初始位置坐标为 ${P_{{\rm{T}}\left( 0 \right)}}$;
(3) 对所有初始化位置坐标粒子求均值获得目标和诱饵的联合初始位置,即${\chi _0} = (1/I)\sum\nolimits_{i = 1}^I {{{\left[ {{\chi _0}} \right]}_i}} $。令直角坐标系下目标和诱饵的初始联合状态向量粒子为$\left[ {s\left( 0 \right)} \right]_{i = 1}^I = {\left[ {\begin{array}{*{20}{c}} {\left[ {\chi _0^{\rm{T}}} \right]_{i = 1}^I}&{\dot \chi _0^{\rm{T}}} \end{array}} \right]^{\rm{T}}}$。其中$\dot \chi _0^{\rm{T}}$为二者的初始联合速度向量,可通过初始假设或者采用两点法(两点距离差与时间的比值求解速度)获得;
(4) 利用步骤(3)获得的${\chi _0}$,根据状态方程式(19)由 ${P_0}$预测位置坐标 ${P_{1/0}}$,跟踪雷达则根据比例制导律[17]获得对应的位置坐标 ${P_{{\rm{T}}(1/0)}}$,同时令 $k = 1$;
步骤2 观测获取
(5) 由制导雷达位置坐标 ${P_{{\rm{T}}(k/k - 1)}}$,压制比 $K$以及 $P_{k/k - 1}^1$和$P_{k/k - 1}^2$中对应的方位和俯仰成分,根据两点源干扰原理及式(1)获得$k$时刻跟踪雷达波束指向的方位和俯仰 $\left( {{\theta _{{\rm{a}},k}},{\theta _{{\rm{e}},k}}} \right)$;
(6) 将坐标系原点移到跟踪雷达的位置坐标${P_{{\rm{T}}(k/k - 1)}}$,并根据式(7)和式(8)获得M个子脉冲的雷达观测信号${\bf{Z}}_1^M\left( k \right) = \left\{ {{{\bf{Z}}_k}(m)} \right\}_{m = 1}^M$;
步骤3 粒子传播
(7) 每个粒子按照状态转移概率进行传播,确保条件概率密度函数$p\left( {{{\left[ {{\chi _k}} \right]}_i}\left| {{{\left[ {{\chi _{k - 1}}} \right]}_i}} \right.} \right)$满足式(19);令${\left[ {s\left( {k|k - 1} \right)} \right]_i} = F{\left[ {s\left( {k - 1} \right)} \right]_i}$,从状态向量粒子${\left[ {s\left( {k|k - 1} \right)} \right]_i}$中获得对应的位置坐标粒子${\left[ {{\chi _{k|k - 1}}} \right]_i}$;
(8) 在传播的粒子中加入扰动项θ,令${\left[ {\chi _{k|k - 1}^u} \right]_i}$,并设置剔除门限使得产生的位置粒子${\left[ {\chi _{k|k - 1}^u} \right]_i}$始终处于雷达波束和距离波门内;
(9) 根据式(3)和式(4)将位置向量粒子${\left[ {\chi _{k|k - 1}^u} \right]_i}$转化成对应的目标和诱饵联合参数向量粒子${\left\{ {\lambda _k^u} \right\}_i}$;
步骤4 重要性采样与重采样
(10) 根据式(10)计算粒子的重要性权${W^i} = p\left( {{Z_k}(m)\left| {{{\left[ {\lambda _k^u} \right]}_i}} \right.} \right)$,并进行归一化得 ${w^i} = {W^i}/\sum\nolimits_{i = 1}^I {{W^i}} $;
(11) 将归一化重要性权${w^i}$分配给粒子${\left[ {\lambda _k^u} \right]_i}$,并对粒子集$\left\{ {{{\left[ {\lambda _k^u} \right]}_i}} \right\}_{i = 1}^I$进行重采样获得采样后的参数粒子集$\left\{ {{{\left[ {\lambda _k^{{\rm{sam}}}} \right]}_i}} \right\}_{i = 1}^I$;根据式(5)和式(2)将重采样后的参数粒子集$\left\{ {{{\left[ {\lambda _k^{{\rm{sam}}}} \right]}_i}} \right\}_{i = 1}^I$转化成位置粒子${\left[ {{\chi _k}} \right]_i}$;
(12) 对所有位置向量粒子求均值获得$k$时刻目标和诱饵的联合位置坐标,即${\chi _k} = (1/I)\sum\nolimits_{i = 1}^I {{{\left[ {{\chi _k}} \right]}_i}} $,并且根据状态方程式(19)由$k$时刻坐标${P_k}$预测$k + 1$时刻目标和诱饵的联合位置坐标=${P_{k + 1|k}}$,同时跟踪雷达根据比例导引律获得$k + 1$时刻对应的位置坐标${P_{{\rm{T}}(k + 1/k)}}$;
步骤5 时间递进与状态递归
(13) 令$k + 1 \to k$,循环递归到步骤(2)。
5 实验验证本节以末制导尾追攻击条件下空射诱饵干扰为例,通过蒙特卡罗仿真实验验证联合跟踪算法的性能特点。实验中选取诱饵释放后形成平稳伴飞到目标与诱饵相对于跟踪雷达的张角达到半波束宽度这一过程,即二者始终处于跟踪雷达的波束内。仿真实验参数设置如表 1所示。
根据表 1的参数设置,可得仿真场景下的飞行曲线如图 3所示。
| 表 1 仿真参数设置 Tab.1 Simulation parameter setting |
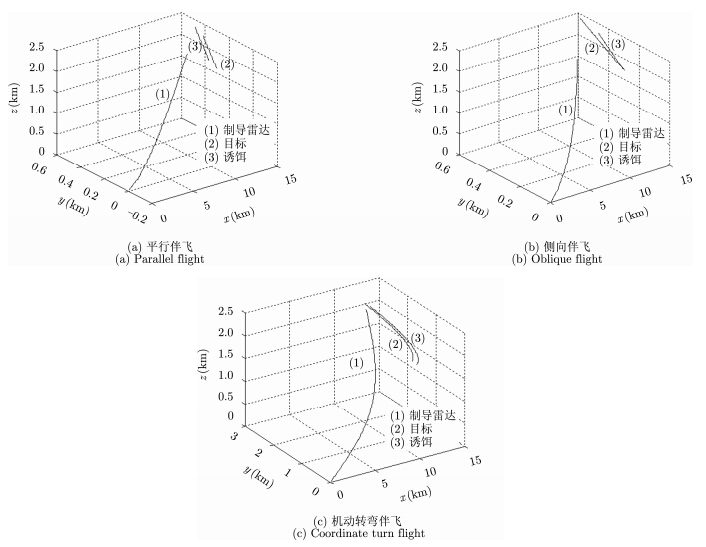 | 图 3 尾追攻击场景下的飞行曲线Fig. 3 Track trajectories under two flight modes |
采用多次蒙特卡罗实验下跟踪滤波轨迹与实际飞行轨迹的均方误差(RMSE)来评测联合跟踪算法的性能,其中蒙特卡罗实验200次。试验中设定目标信噪比${\Re _{\rm{T}}} = 20 {\rm{dB}}$且固定不变,诱饵的信噪比由干扰压制比K来确定。分别取K=1,2,4,8四种压制比条件进行跟踪性能评测。
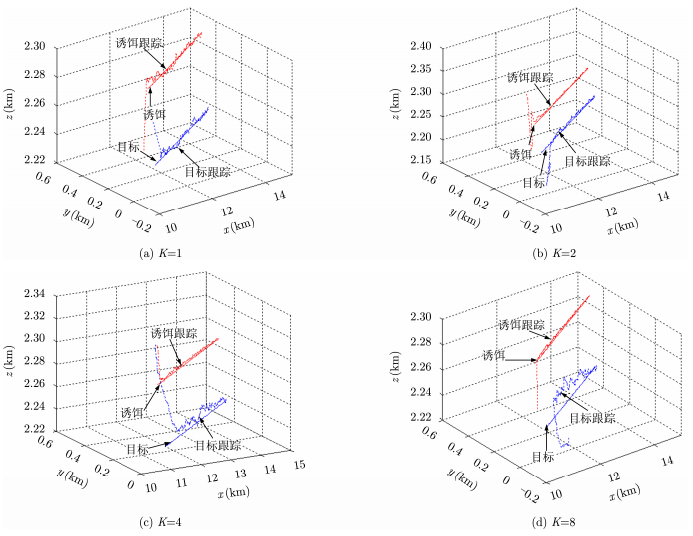
实验 1 平行伴飞模式下,依次选取不同干扰压制比,采用图 2的联合跟踪处理流程可得4种典型干扰条件下目标与诱饵的联合跟踪曲线如图 4所示。
 | 图 4 平行伴飞模式下目标与诱饵的联合跟踪曲线Fig. 4 Jointtracking trajectory of the unresolved target and decoy under parallel flightmode |
图 4的跟踪曲线表明在诱饵平行伴飞模式下,联合跟踪算法能够实现4种典型干扰条件下目标与诱饵的同时跟踪。由干扰原理可知,压制比越大,波束中心越偏离目标而靠近诱饵。图 4 (a)中目标和诱饵功率相等,雷达天线电轴指向二者的几何中心,此时雷达对目标和诱饵的跟踪完全对等。随着压制比的增加,图 4 (b)-图 4 (d)中雷达天线逐渐偏向诱饵,压制比越大,雷达对诱饵的跟踪曲线越平稳,而目标的跟踪曲线则起伏越大,跟踪性能下降。
对图 4平行伴飞模式下的联合跟踪处理进行200次蒙特卡罗实验,可得对应的目标与诱饵联合跟踪RMSE曲线如图 5所示。
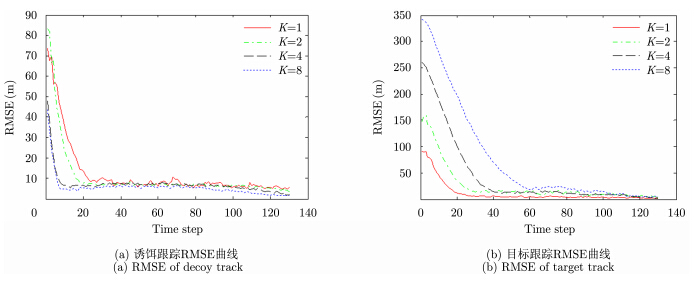 | 图 5 平行伴飞模式下目标与诱饵联合跟踪RMSE曲线Fig. 5 Tracking RMSE ofunresolved target and decoy under parallel flight |
图 5的RMSE曲线表明,在跟踪初始阶段,由于粒子迭代次数少,跟踪尚未收敛,目标和诱饵的跟踪RMSE都较大。随着粒子迭代的增加,跟踪逐渐熟练,性能逐渐改善,RMSE随之减小。仿真时刻$k > 40$时,诱饵跟踪RMSE减小到10 m以下,同等条件下的目标跟踪RMSE要稍大一些。当仿真时刻$k > 60$时,目标跟踪RMSE同样下降到10 m左右,满足常规空中目标跟踪的精度要求。同时,图 5表明压制比K越大,诱饵跟踪的RMSE越小,目标跟踪的RMSE越大。
实验 2 侧向伴飞模式下,依次选取4种不同干扰压制比,采用图 2的联合跟踪处理流程可得4种典型干扰条件下目标与诱饵的联合跟踪曲线如图 6所示。
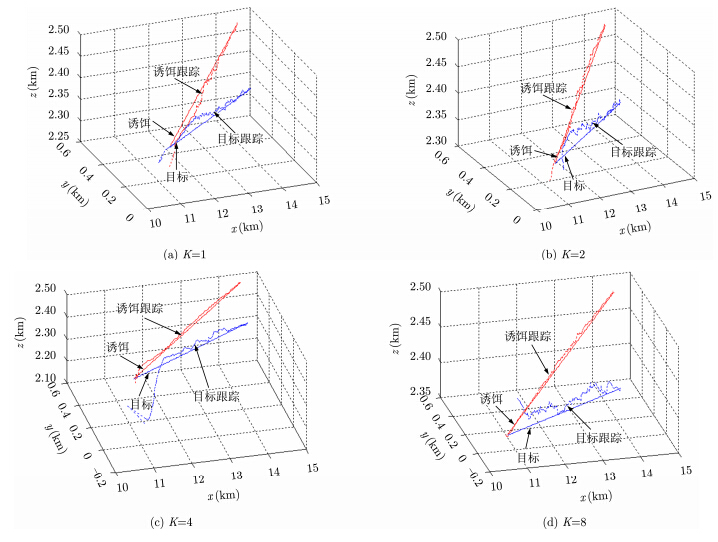 | 图 6 侧向伴飞模式下目标与诱饵的联合跟踪曲线Fig. 6 Jointtracking trajectory of the unresolved target and decoy under oblique flightmode |
图 6中,由于侧向伴飞模式下目标与诱饵是逐步分离的,在跟踪初始阶段,二者的分离程度很低,并且粒子的迭代次数较少,联合跟踪的效果不理想。随着目标和诱饵分离程度的加剧以及粒子迭代的深入,联合跟踪效果逐步改善,曲线逐步平稳。同时,干扰压制比对联合跟踪性能影响仍然较大,随着压制比的增加,诱饵的跟踪曲线逐渐平整,跟踪性能改善;而目标的跟踪曲线则起伏很大,跟踪性能有所下降。
对图 6侧向伴飞模式下的联合跟踪滤波进行200次蒙特卡罗实验,可得对应的目标与诱饵联合跟踪RMSE曲线如图 7所示。
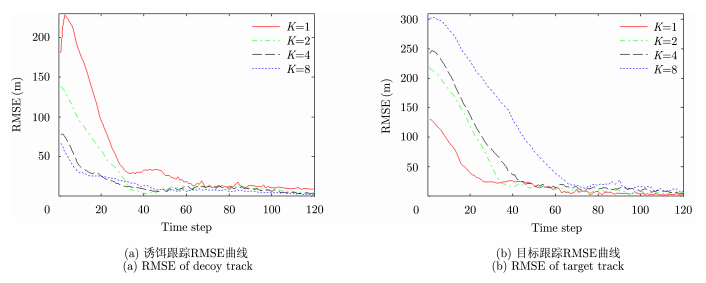 | 图 7 侧向伴飞形式下目标与诱饵联合跟踪RMSE曲线Fig. 7 Tracking RMSE ofunresolved target and decoy under oblique flight |
图 7中,初始跟踪阶段由于目诱分离程度低以及粒子迭代次数少,目标和诱饵的跟踪RMSE都比较大。随着粒子迭代的增加,跟踪逐渐收敛,RMSE随之下降。当仿真时刻$k \ge 60$时,二者的跟踪RMSE下降到12 m左右,达到了常规空中目标的跟踪精度要求。同时,压制比的增加使得诱饵跟踪RMSE减小,目标跟踪RMSE增加,这一结论与图 6的结果是一致的。
实验 3 转弯伴飞模式下,依次选取4种不同干扰压制比,采用图 2的联合跟踪处理流程可得4种典型干扰条件下目标与诱饵的联合跟踪曲线如图 8所示。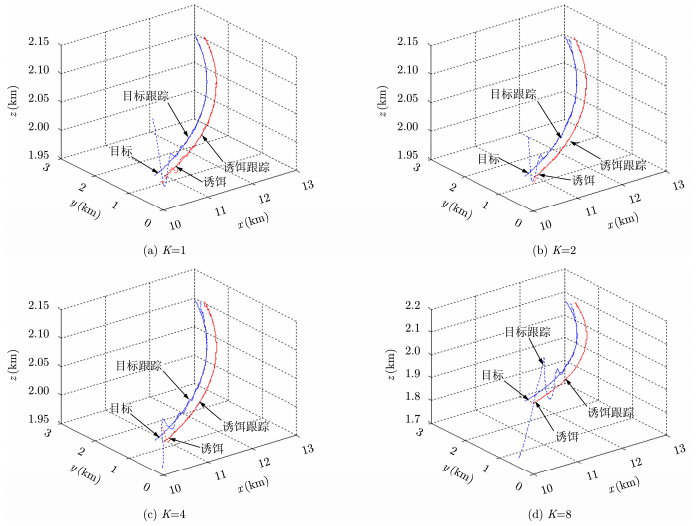 | 图 8 转弯伴飞模式下目标与诱饵的联合跟踪曲线Fig. 8 Joint tracking trajectory of the unresolved target and decoy under coordinateturn flight mode |
图 8跟踪曲线表明在诱饵转弯伴飞模式下,联合跟踪算法仍然能够实现4种典型干扰条件下目标与诱饵的同时跟踪。同样由于干扰压制比的逐渐增大,雷达波束中心逐渐偏离目标而偏向诱饵,诱饵对应的跟踪曲线逐渐平稳,而目标对应的跟踪曲线起伏逐渐增大。
对图 8侧向伴飞模式下的联合跟踪滤波进行200次蒙特卡罗实验,可得对应的目标与诱饵联合跟踪RMSE曲线如图 9所示。
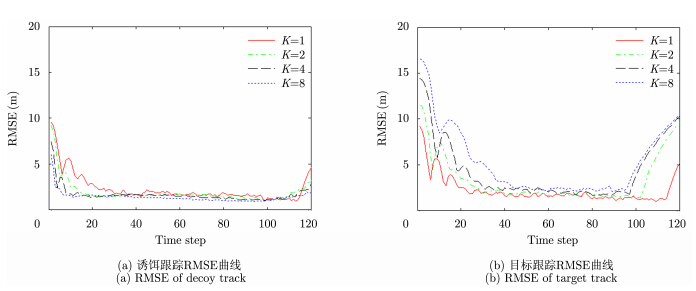 | 图 9 转弯伴飞形式下目标与诱饵联合跟踪RMSE曲线Fig. 9 Tracking RMSE of unresolved target and decoy under coordinate turnflight |
图 9的RMSE曲线表明,在机动转弯伴飞模式下,随着时间的递进以及粒子迭代的进行,联合跟踪处理的RMSE逐渐减小。当仿真时刻$k \ge 30$时,二者的跟踪RMSE可以下降到5 m左右,满足雷达稳定跟踪的精度要求。对比图 5,图 7和图 9的仿真结果,可以看到图 9中对应的目标和诱饵的RMSE要小于其它两种模式下的RMSE,造成这一现象的原因是在进行协同转弯过程中,为避免目标和诱饵航迹出现交叉,设定二者之间的间距比其它两种模式要大一些,因此在跟踪滤波过程中,同一目标或诱饵的状态粒子差异也大一些,使得同一目标或诱饵的状态粒子能够迅速收敛,从而使得联合跟踪的RMSE较小。同时可以看到,在目标跟踪的后期,由于此时目标已经靠近雷达波束的边沿,跟踪误差增大。
6 结束语针对末制导有源诱饵干扰条件下不可分辨目标与诱饵引起回波混叠和观测不确定性所导致的常规跟踪处理失效问题,本文结合干扰特性推导了不可分辨多目标信号模型,基于干扰检测信息,采用粒子联合状态估计,直接对接收机和差通道信号进行处理,绕开观测提取、参数测量以及数据关联过程,实现了波束内不可分辨目标与诱饵的联合跟踪。尾追攻击场景下的实验表明,在典型干扰压制比K=2~8条件下联合跟踪算法的${\rm{RMSE}} \le {\rm{12 m}}$,满足目标跟踪以及抗干扰需求。
目标与诱饵的联合跟踪并不是制导雷达的终极目标,雷达系统需要利用获取的跟踪状态和航迹,结合干扰样式、攻击态势、几何构型、功率特点等多种信息完成身份辨识和目标选择,调整雷达波束指向实现准确引导。目标的识别和选择是下一步需要重点研究的问题。
| [1] |
张涛, 于雷, 周中良. 超视距空战中空射诱饵弹协同接敌策略[J]. 弹箭与制导学报, 2014, 34(1): 60-65.Zhang Tao, YuLei, and Zhou Zhong-liang. Coordinated engagement strategy for MALD and fighterin beyond- visual-range air combat[J]. Journal of Projectiles, Rockets,Missile and Guidance, 2014, 34(1): 60-65.
( 1) 1)
|
| [2] |
ZhangX, Willett P K, and Bar-shalom Y. Monopulse radar detection and localization ofmultiple unresolved targets via joint bin processing[J]. IEEE Transactionson Signal Processing, 2005, 53(4): 1225-1236.
( 3) 3)
|
| [3] |
NandakumaranN, Sinha A, and Kirubarajan T. Joint detection and tracking of unresolved targetswith monopulse radar[J]. IEEE Transactions on Aerospace and ElectronicSystems, 2008, 44(4): 1326-1341.
( 1) 1)
|
| [4] |
HueC, LeCadre J-P, and Perez P. Tracking multiple objects with particle filtering[J].IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 791-812.
( 1) 1)
|
| [5] |
宋志勇, 肖怀铁. 基于角闪烁效应的拖曳式诱饵干扰存在性检测[J]. 信号处理, 2011, 27(4): 522-528.Song Zhi-yongand Xiao Huai-tie. Detection of presence of towed radar active decoys based onangle glint[J]. Signal Processing, 2011, 27(4): 522-528.
( 1) 1)
|
| [6] |
IsaacA, Willett P K, and Bar-Shalom Y. Quickest detection and tracking of spawningtargets using monopulse radar channel signals[J]. IEEE Transactions onSignal Processing, 2008, 56(3): 1302-1308.
( 1) 1)
|
| [7] |
IsaacA, Willett P K, and Bar-Shalom Y. MCMC methods for tracking two closely spacedtargets using monopulse radar channel signals[J]. IET Radar, Sonar &Navigation, 2007, 1(3): 221-229.
( 1) 1)
|
| [8] |
LevanonN. Radar Principle[M]. New York: Wiley, 1988: 241-247.
( 2) 2)
|
| [9] |
Zhang X, Willett P K, and Bar-shalom Y. Detection and localizationof multiple unresolved extended targets via monopulse radar signal processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 455-472.
( 1) 1)
|
| [10] |
赵峰, 杨建华, 丹梅. 基于距离闪烁效应的不可分辨多目标存在性检测[J]. 电子学报, 2008, 36(12): 2290-2298. Zhao Feng, YangJian-hua, and Dan Mei. Detection of presence of multiple unresolved targetbased on range glint[J]. Acta Electronic Sinica, 2008, 36(12): 2290-2298. (  1) 1)
|
| [11] |
吴伟, 尹成友. 一种用于多目标跟踪的增强型SMC-PHD滤波算法[J]. 雷达学报, 2012, 1(4): 406-413.Wu Wei and YinCheng-you. An improved SMC-PHD filter for multiple targets tracking[J]. Journalof Radars, 2012, 1(4): 406-413.
( 1) 1)
|
| [12] |
ArulampalamM S, Maskell S, Gordon N, et al.. A tutorial on particle filters foronline nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions onSignal Processing, 2002, 50(2): 174-188.
( 1) 1)
|
| [13] |
SongZhi-yong, Xiao Huai-tie, Zhu Yi-long, et al.. A novel approach to detectthe unresolved towed decoy in terminal guidance[J]. Chinese Journal ofElectronics, 2012, 21(2): 367-373.
( 1) 1)
|
| [14] |
SahaS and Gustafsson F. Particle filtering with dependent noise processes[J]. IEEETransactions on Signal Processing, 2012, 60(9): 4497-4508.
( 1) 1)
|
| [15] |
ZuoJun-yi, Jia Ying-na, and Gao Quan-xue. Simplified unscented particle filter fornonlinear/non-Gaussian Bayesian estimation[J]. Journal of SystemsEngineering and Electronics, 2013, 24(3): 537-544.
( 1) 1)
|
| [16] |
MonakovA. Maximum-likelihood estimation of parameters of an extended target intracking monopulse radars [J]. IEEE Transactions on Aerospace and ElectronicSystems, 2012, 48(3): 2653-2665 .
( 1) 1)
|
| [17] |
冯德龙, 杨锁昌, 田再克, 等. 一种改进的扩展比例导引律及其仿真[J]. 火力与指挥控制, 2014, 39(5): 161-163. Feng De-long,Yang Suo-chang, Tian Zai-ke, et al.. An improved expansion proportionalguidance law and simulation study[J]. Fire Control & Command andControl, 2014, 39(5): 161-163. (  1) 1)
|


