② 中国科学院大学 北京 100049
② University of Chinese Academy of Sciences, Beijing 100049, China
多波段合成孔径雷达(Synthetic Aperture Radar, SAR)具有在多个波段同时高分辨成像的能力[1]。其中,高频波段SAR能够显示场景的细节特征,可以提供结构、纹理等信息;低频波段SAR具有很强的穿透能力,可以发现隐蔽目标,挖掘地表下的结构[2, 3]。与传统的单波段SAR相比,多波段SAR可以大大提高SAR所获取目标的信息量,能较为全面地描述目标的特性,已成为SAR成像技术发展的一个重要趋势[4, 5]。
多波段SAR图像必须经过图像融合才能将各自优势综合起来,而图像融合之前必须进行图像配准。然而,不同波段的电磁波与地物散射机理不同,导致多波段SAR图像之间纹理特征差异显著、灰度动态范围较大并且可对比特征下降[6, 7]。传统的基于相关的图像配准和基于特征的图像配准方法主要针对波段、分辨率和景物特征等一致或接近的图像[3, 8],计算量较大,无法达到快速、实时、自动配准的要求,难以实现高精度的图像配准。因此,已有的图像配准方法无法满足机载多波段SAR图像高精度配准的要求[9]。
对于机载多波段SAR系统,由于多部SAR子系统搭载在同一载机平台上,具有同步性强、多部SAR飞行轨迹平行等优势,可以考虑通过控制机载SAR的各种误差因素,在对SAR获取的数据进行成像处理的过程中同时完成图像的配准。这样可以提高处理速度,有利于实时处理。目前,德国宇航中心(DLR)已对F-SAR的图像配准精度开展了定量的研究,其X, S, L波段子系统距离向和方位向的图像配准误差均在0.2 m内[10]。国内尚未有关于定量分析多波段SAR图像配准精度方面的报道。
为了保证多波段SAR图像的配准精度,有必要对各种误差的影响进行定量的分析,而残余运动,即运动测量系统的测量误差是其中一个重要的因素。为此,本文详细分析了残余运动对多波段SAR图像配准精度的影响,并通过仿真实验验证了分析结果的正确性。本文结构安排如下:第2节对残余运动误差进行了建模;第3节分析了残余运动误差对SAR成像几何定位的影响,为第4节的研究奠定基础;第4节研究了残余运动对机载多波段图像配准的影响,并利用仿真实验进行了验证;第5节总结全文。
2 残余运动误差模型载机平台上配备的基于IMU/GPS (Inertial Measurement Unit/Global Positioning System)的组合定位定向系统(Positioning and Orientation System, POS)存在测量误差(称为“残余运动”)[11],测得的运动误差与真实运动误差之间存在残余运动误差。本文将POS关于载机位置的测量误差称为残余平动误差,关于载机姿态的测量误差称为残余姿态误差。
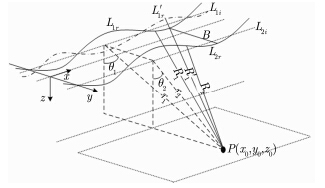
为简化分析,图 1以两部SAR子系统为例,给出机载多波段SAR系统存在残余运动误差时的几何模型。虚线${L_{1i}}$和${L_{2i}}$分别表示两部SAR子系统不存在残余运动误差时,进行高精度运动补偿后的天线相位中心(Antenna Phase Center, APC)轨迹,${r_1}$和${r_2}$为各自的最近斜距,${\theta _1}$和${\theta _2}$为对应的下视角,B为基线。实线${L_{1r}}$和${L_{2r}}$表示存在残余平动误差时,完成运动补偿后两部SAR子系统的APC轨迹,点划线$L_{1r}^{'}$和实线${{L}_{2r}}$表示存在残余姿态误差时,完成运动补偿后两部SAR子系统的APC轨迹。
|
图 1 机载多波段SAR系统存在残余运动时的几何模型 Fig.1 Geometric model for airborne multi-band SAR in presence of residual motion |
残余平动误差造成SAR系统APC位置误差,残余姿态误差通过IMU与APC之间的杠杆臂传递也会导致APC位置误差。所以,可将残余平动误差和残余姿态误差归结为APC位置误差进行分析。设APC位置误差为:
| $\Delta A = {\left[ {\begin{array}{*{20}{c}} {dx}&{dy}&{dz} \end{array}} \right]^{\rm{T}}}$ | (1) |
(1) 残余平动误差形式
文献[12]指出,残余运动误差为低频形式,本文采用3次多项式对残余平动误差进行近似,假设残余平动误差引起的APC位置误差为:
| $\Delta A = \left[ {\begin{array}{*{20}{c}} {dx}\\ {dy}\\ {dz} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_x}{\eta ^3} + {b_x}{\eta ^2} + {c_x}\eta + {d_x}}\\ {{a_y}{\eta ^3} + {b_y}{\eta ^2} + {c_y}\eta + {d_y}}\\ {{a_z}{\eta ^3} + {b_z}{\eta ^2} + {c_z}\eta + {d_z}} \end{array}} \right]$ | (2) |
(2) 残余姿态误差形式
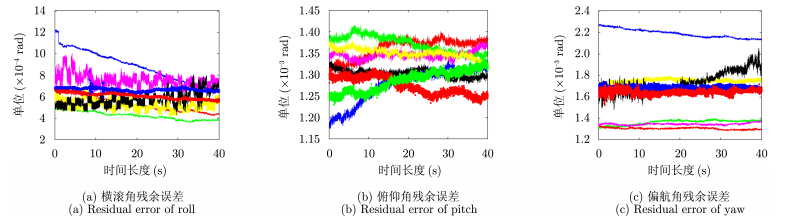
图 2(a)-图 2(c)中不同颜色的线段表示高精度的POS AV610与另一精度较低的POS系统同时测得的同一平台的横滚角、俯仰角和偏航角分别作差的结果(以40 s为间隔,多次重复实验),本文利用该结果近似代表残余姿态误差。从图 2中可以看出,二者作差的结果量级为10-3 rad,在40 s内的变化趋势为低频形式。
|
图 2 POS AV610与某较低精度POS同时测得的同一平台的姿态角作差的结果 Fig.2 Results of the difference about attitude angles measured by POS AV610 and another lower-precision POS |
根据上述规律,假设残余姿态误差的形式为:
| $\left. \begin{array}{l} \Delta {\theta _r}\left( \eta \right) = {k_r}{\eta ^3} + {l_r}{\eta ^2} + {m_r}\eta + {n_r}\\ \Delta {\theta _p}\left( \eta \right) = {k_p}{\eta ^3} + {l_p}{\eta ^2} + {m_p}\eta + {n_p}\\ \Delta {\theta _y}\left( \eta \right) = {k_y}{\eta ^3} + {l_y}{\eta ^2} + {m_y}\eta + {n_y} \end{array} \right\}$ | (3) |
残余运动误差造成的APC方位位置误差很小,而且沿着雷达视线(Line Of Sight, LOS)方向的APC误差位置是导致SAR图像相位误差的主要因素。因此,本文不再考虑APC方位向位置误差的影响。APC距离向和高度向的位置误差投影到LOS方向的残余运动误差为[13]:
| $\delta {e_0} = - dy \cdot \sin \theta + dz \cdot \cos \theta $ | (4) |
前人已分析了线性、2次残余运动误差对SAR成像几何定位的影响[14]以及3次残余运动误差对成像质量的影响[15],但对3次残余运动误差造成的SAR几何定位误差未作定量的分析。本节将重点推导3次残余运动误差与SAR成像几何定位误差的函数关系式。此外,为方便本文后续的推导分析,本节给出线性、2次残余运动误差对SAR成像几何定位影响的相关结论。
根据第2节中给出的残余运动误差模型,可将LOS方向的残余运动误差在$\eta = {\eta _0}$处表示为:
| $\begin{align} & \delta {{e}_{0}}(\eta )\approx \frac{1}{6}\overset{\centerdot \centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,\cdot {{\left( \eta -{{\eta }_{0}} \right)}^{3}}+\frac{1}{2}\overset{\centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,\cdot {{\left( \eta -{{\eta }_{0}} \right)}^{2}} \\ & \qquad\qquad +\overset{\centerdot }{\mathop{\delta {{e}_{0}}}}\,\cdot \left( \eta -{{\eta }_{0}} \right)+\delta {{e}_{0}} \\ \end{align}$ | (5) |
其中,$\overset{\centerdot }{\mathop{\delta {{e}_{0}}}}\,,\overset{\centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,,\overset{\centerdot \centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,$和$\delta {{e}_{0}}$分别为残余运动误差$\delta {{e}_{0}}(\eta )$在成像点目标零多普勒时刻${{\eta }_{0}}$处的1阶、2阶、3阶导数和常数项。
由文献[14]可知,线性残余运动误差
| $\delta {{e}_{0}}(\eta )=\overset{\centerdot }{\mathop{\delta {{e}_{0}}}}\,\cdot \left( \eta -{{\eta }_{0}} \right)+\delta {{e}_{0}}$ | (6) |
| $\left. \begin{align} & \Delta x=-\frac{{{r}_{0}}}{V}\cdot \overset{\centerdot }{\mathop{\delta {{e}_{0}}}}\, \\ & \Delta r\approx \delta {{e}_{0}} \\ \end{align} \right\}$ | (7) |
2次残余运动误差
| $\delta {{e}_{0}}(\eta )=\frac{1}{2}\overset{\centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,\cdot {{\left( \eta -{{\eta }_{0}} \right)}^{2}}$ | (8) |
当残余运动误差模型中仅含3次项时,式(5)简化为:
| $\delta {{e}_{0}}(\eta )=\frac{1}{6}\overset{\centerdot \centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,\cdot {{\left( \eta -{{\eta }_{0}} \right)}^{3}}$ | (9) |
| $\delta {{e}_{0}}(\eta )=\frac{T_{a}^{3}}{120}\overset{\centerdot \centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,{{P}_{3}}(\eta )+\frac{T_{a}^{3}}{80}\overset{\centerdot \centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,{{P}_{1}}(\eta )$ | (10) |
$\begin{array}{l} {P_3}(\eta ) = \frac{1}{2}\left( {5{{\left( {\frac{{2\left( {\eta - {\eta _0}} \right)}}{{{T_a}}}} \right)}^3} - 3 \cdot \frac{{2\left( {\eta - {\eta _0}} \right)}}{{{T_a}}}} \right)\\ {P_1}(\eta ) = \frac{{2\left( {\eta - {\eta _0}} \right)}}{{{T_a}}} \end{array}$
为合成孔径时间。式(10)中的第2项为残余运动误差式(9)中分离得到的线性项:| $\frac{T_{a}^{3}}{80}\overset{\centerdot \centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,{{P}_{1}}(\eta )=\frac{T_{a}^{2}}{40}\overset{\centerdot \centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\,\left( \eta -{{\eta }_{0}} \right)$ | (11) |
| $\Delta x=-\frac{{{r}_{0}}}{V}\left( \frac{T_{a}^{2}}{40}\overset{\centerdot \centerdot \centerdot }{\mathop{\delta {{e}_{0}}}}\, \right)$ | (12) |
通过分析上述的推导结果可知:
线性残余运动误差造成点目标的方位向几何定位误差与残余运动误差的线性项系数$\overset{\centerdot }{\mathop{\delta {{e}_{0}}}}\,$、最近斜距${{r}_{0}}$成正比,与载机速度$V$成反比,与波长无关;距离向几何定位误差由常数残余运动误差引起。
2次残余运动误差会造成图像散焦,但在可成像条件下不会造成几何定位误差。
3次残余运动误差造成的方位向几何定位误差$\Delta x$与$T_{a}^{2}$成正比,即相同系数的3次残余运动误差造成点目标的方位向几何定位误差与合成孔径时间的平方成正比。
4 残余运动对多波段SAR图像配准的影响分析机载多波段SAR系统中,不同波段合成孔径时间不同,因此,对应孔径内的残余平动误差形式不同。此外,各波段SAR子系统天线之间存在基线,残余姿态误差通过杠杆臂的传递引起各波段SAR系统的APC位置误差不同,导致各波段在对应合成孔径时间内不同的残余运动误差。这些都会影响机载多波段SAR图像的精确配准。
针对上述问题,本节首先推导了残余姿态误差与APC位置误差的关系式,然后分析了各波段SAR系统在对应合成孔径时间内不同的残余运动误差对机载多波段SAR图像配准的影响,并通过仿真实验进行验证。
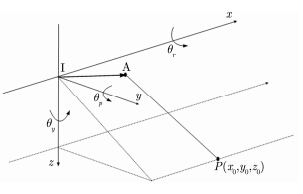
4.1 残余姿态误差与APC位置误差的关系式SAR系统天线与IMU的几何关系如图 3所示,A代表APC, I代表IMU, $P({{x}_{0}},{{y}_{0}},{{z}_{0}})$代表场景中观测点目标, ${\theta _r},$,${\theta _p},$,${\theta _y},$分别表示横滚角、俯仰角、偏航角。
|
图 3 机载SAR系统天线与IMU的几何关系 Fig.3 Geometricrelationship between the SAR system antennaand the IMU |
设IMU和APC的初始位置分别为(0,0,0)和$\left( {{x}_{\text{A}}},{{y}_{\text{A}}},{{z}_{\text{A}}} \right)$,那么由IMU指向APC的杠杆臂矢量为${{L}_{\text{IA}}}={{[\begin{matrix} {{x}_{\text{A}}} & {{y}_{\text{A}}} & {{z}_{\text{A}}} \\ \end{matrix}]}^{\text{T}}}$ 。坐标旋转矩阵为[17]:
| ${{M}_{r}}=\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & \cos {{\theta }_{r}} & -\sin {{\theta }_{r}} \\ 0 & \sin {{\theta }_{r}} & \cos {{\theta }_{r}} \\ \end{matrix} \right]$ | (13) |
| ${{M}_{p}}=\left[ \begin{matrix} \cos {{\theta }_{p}} & 0 & \sin {{\theta }_{p}} \\ 0 & 1 & 0 \\ -\sin {{\theta }_{p}} & 0 & \cos {{\theta }_{p}} \\ \end{matrix} \right]$ | (14) |
| ${{M}_{y}}=\left[ \begin{matrix} \cos {{\theta }_{y}} & -\sin {{\theta }_{y}} & 0 \\ \sin {{\theta }_{y}} & \cos {{\theta }_{y}} & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]$ | (15) |
姿态角误差通过IMU与APC之间的杠杆臂传递影响APC的位置。所以,当POS测量的载机姿态信息不准确,即存在残余姿态误差时,APC的测量位置和真实位置不同,APC位置存在误差。设天线姿态角的测量值为${{\widetilde{\theta }}_{r}},{{\widetilde{\theta }}_{p}},{{\widetilde{\theta }}_{y}}$,真实值为${{\theta }_{r}},{{\theta }_{p}},{{\theta }_{y}}$,那么APC的位置误差为:
| $\begin{align} & \Delta A=\left[ \begin{matrix} dx \\ dy \\ dz \\ \end{matrix} \right]={{M}_{r}}\left( {{\widetilde{\theta }}_{r}} \right){{M}_{p}}\left( {{\widetilde{\theta }}_{p}} \right){{M}_{y}}\left( {{\widetilde{\theta }}_{y}} \right){{L}_{\text{IA}}} \\ & \qquad\qquad\qquad-{{M}_{r}}\left( {{\theta }_{r}} \right){{M}_{p}}\left( {{\theta }_{p}} \right){{M}_{y}}\left( {{\theta }_{y}} \right){{L}_{\text{IA}}} \\ \end{align}$ | (16) |
在小姿态角条件下,正余弦函数的2次及更高次项可以忽略,即$\sin \theta \approx \theta , \cos \theta \approx 1$。因此,由残余姿态误差引起的APC位置误差可近似为[18]:
| $\Delta A=\left[ \begin{matrix} 0 & -\Delta {{\theta }_{y}} & \Delta {{\theta }_{p}} \\ \Delta {{\theta }_{y}} & 0 & -\Delta {{\theta }_{r}} \\ -\Delta {{\theta }_{p}} & \Delta {{\theta }_{r}} & 0 \\ \end{matrix} \right]{{L}_{\text{IA}}}$ | (17) |
由式(17)可知,残余姿态误差导致的APC位置误差$\Delta A$不仅与残余姿态误差$\Delta {{\theta }_{r}},\Delta {{\theta }_{p}},\Delta {{\theta }_{y}}$有关,而且与杠杆臂矢量${{L}_{\text{IA}}}$有关。
(1) 当杠杆臂沿交轨方向时,杠杆臂矢量为:
| ${{L}_{\text{IA}}}={{\left[ \begin{matrix} 0 & {{y}_{\text{A}}} & 0 \\ \end{matrix} \right]}^{\text{T}}}$ | (18) |
| $\begin{align} & \Delta A\left( \eta \right)=\left[ \begin{matrix} dx \\ dy \\ dz \\ \end{matrix} \right]=\left[ \begin{matrix} -\Delta {{\theta }_{y}}\left( \eta \right){{y}_{\text{A}}} \\ 0 \\ \Delta {{\theta }_{r}}\left( \eta \right){{y}_{\text{A}}} \\ \end{matrix} \right] \\ & ={{y}_{\text{A}}}\left[ \begin{matrix} -\left( {{k}_{y}}{{\eta }^{3}}+{{l}_{y}}{{\eta }^{2}}+{{m}_{y}}\eta +{{n}_{y}} \right) \\ 0 \\ {{k}_{r}}{{\eta }^{3}}+{{l}_{r}}{{\eta }^{2}}+{{m}_{r}}\eta +{{n}_{r}} \\ \end{matrix} \right] \\ \end{align}$ | (19) |
由式(19)可知,残余姿态误差导致APC位置在方位向和高度向存在误差。APC在方位向和高度向的位置误差形式分别由偏航角和横滚角的形式决定,幅度与杠杆臂的长度成正比。
(2) 当杠杆臂沿顺轨方向时,杠杆臂矢量为:
| ${{L}_{\text{IA}}}={{\left[ \begin{matrix} {{x}_{\text{A}}} & 0 & 0 \\ \end{matrix} \right]}^{\text{T}}}$ | (20) |
| $\begin{align} & \Delta A\left( \eta \right)=\left[ \begin{matrix} dx \\ dy \\ dz \\ \end{matrix} \right]=\left[ \begin{matrix} 0 \\ \Delta {{\theta }_{y}}\left( \eta \right){{x}_{\text{A}}} \\ -\Delta {{\theta }_{p}}\left( \eta \right){{x}_{\text{A}}} \\ \end{matrix} \right] \\ & ={{x}_{\text{A}}}\left[ \begin{matrix} 0 \\ {{k}_{y}}{{\eta }^{3}}+{{l}_{y}}{{\eta }^{2}}+{{m}_{y}}\eta +{{n}_{y}} \\ -\left( {{k}_{p}}{{\eta }^{3}}+{{l}_{p}}{{\eta }^{2}}+{{m}_{p}}\eta +{{n}_{p}} \right) \\ \end{matrix} \right] \\ \end{align}$ | (21) |
由式(21)可知,残余姿态误差导致APC位置在距离向和高度向存在误差。APC在距离向和高度向的位置误差形式分别由偏航角和俯仰角的形式决定,幅度与杠杆臂长度成正比。
至此,残余姿态误差已通过杠杆臂的传递转化为APC位置误差。
4.2 残余运动误差的影响分析假设杠杆臂沿交轨方向,如图 1所示。天线1的杠杆臂矢量为:
| ${{L}_{\text{IA1}}}={{\left[ \begin{matrix} 0 & -{{y}_{\text{A}}} & 0 \\ \end{matrix} \right]}^{\text{T}}}$ | (22) |
天线2的杠杆臂矢量为:
| ${{L}_{\text{IA2}}}={{\left[ \begin{matrix} 0 & {{y}_{\text{A}}} & 0 \\ \end{matrix} \right]}^{\text{T}}}$ | (23) |
由于高频波段SAR合成孔径时间短,通常只有几秒,残余平动误差可用线性形式近似;反之,低频波段SAR合成孔径时间长,残余平动误差需用更高次的多项式近似。假设天线1和天线2分别为高频波段和低频波段SAR系统的天线,两部天线的残余平动误差分别表示为:
| $\left. \begin{align} & dy1={{c}_{y1}}\eta +{{d}_{y1}} \\ & dz1={{c}_{z1}}\eta +{{d}_{z1}} \\ \end{align} \right\}$ | (24) |
| $\left. \begin{align} & \qquad \qquad \qquad dy2={{a}_{y2}}{{\eta }^{3}}+{{b}_{y2}}{{\eta }^{2}}+{{c}_{y2}}\eta +{{d}_{y2}} \\ & \qquad \qquad \qquad dz2={{a}_{z2}}{{\eta }^{3}}+{{b}_{z2}}{{\eta }^{2}}+{{c}_{z2}}\eta +{{d}_{z2}} \\ \end{align} \right\}$ | (25) |
一般情况下,$B\ll {{r}_{1}}, B\ll {{r}_{2}}, {{r}_{1}}\approx {{r}_{2}}=r, {{\theta }_{1}}\approx {{\theta }_{2}}=\theta $,由式(3),式(4),式(19),式(22)和式(24)可得到天线1在视线方向的残余运动误差为:
| $\begin{align} & \delta {{e}_{1}}(\eta )=-\left( {{c}_{y1}}\eta +{{d}_{y1}} \right)\cdot \sin \theta +\left( {{\left( {{c}_{z1}}\eta +{{d}_{z1}} \right)}^{^{{}}}} \right. \\ & \qquad \qquad \left. +\left( -{{y}_{\text{A}}}\left( {{k}_{r}}{{\eta }^{3}}+{{l}_{r}}{{\eta }^{2}}+{{m}_{r}}\eta +{{n}_{r}} \right) \right) \right)\cdot \cos \theta \\ \end{align}$ | (26) |
由式(3),式(4),式(19),式(23)和式(25)可得到天线2在视线方向的残余运动误差为:
| $\begin{align} & \delta {{e}_{2}}(\eta )=-\left( {{a}_{y2}}{{\eta }^{3}}+{{b}_{y2}}{{\eta }^{2}}+{{c}_{y2}}\eta +{{d}_{y2}} \right)\cdot \sin \theta \\ & \qquad \qquad +\left( \left( {{a}_{z2}}{{\eta }^{3}}+{{b}_{z2}}{{\eta }^{2}}+{{c}_{z2}}\eta +{{d}_{z2}} \right) \right. \\ & \qquad \qquad \left. +\left( {{y}_{\text{A}}}\left( {{k}_{r}}{{\eta }^{3}}+{{l}_{r}}{{\eta }^{2}}+{{m}_{r}}\eta +{{n}_{r}} \right) \right) \right)\cdot \cos \theta \end{align}$ | (27) |
| $\left. \begin{align} & \Delta {{x}_{1}}=-\frac{r}{V}\left[ {{\left( -{{c}_{y1}}\sin \theta +{{c}_{z1}}\cos \theta \right)}^{^{^{^{{}}}}}} \right. \\ & \qquad \qquad \left. -{{m}_{r}}{{y}_{\text{A}}}\cos \theta -\frac{3T_{a1}^{2}}{20}{{k}_{r}}{{y}_{\text{A}}}\cos \theta \right] \\ & \qquad \qquad \Delta {{r}_{1}}=\left( -{{d}_{y1}}\sin \theta +{{d}_{z1}}\cos \theta \right)-{{n}_{r}}{{y}_{\text{A}}}\cos \theta \\ \end{align} \right\}$ | (28) |
| $\left. \begin{align} & \Delta {{x}_{2}}=-\frac{r}{V}\left[ \left( -{{c}_{y2}}\sin \theta +{{c}_{z2}}\cos \theta \right)+{{m}_{r}}{{y}_{\text{A}}}\cos \theta +\frac{3T_{a2}^{2}}{20}\left( \left( -{{a}_{y2}}\sin \theta +{{a}_{z2}}\cos \theta \right)+{{k}_{r}}{{y}_{\text{A}}}\cos \theta \right) \right] \\ & \Delta {{r}_{2}}=\left( -{{d}_{y2}}\sin \theta +{{d}_{z2}}\cos \theta \right)+{{n}_{r}}{{y}_{\text{A}}}\cos \theta \\ \end{align} \right\}$ | (29) |
| $\left. \begin{align} & \Delta {{x}_{r}}=\Delta {{x}_{1}}-\Delta {{x}_{2}}=-\frac{r}{V}\left\{ \left[ -\left( {{c}_{y1}}-{{c}_{y2}} \right)\sin \theta +\left( {{c}_{z1}}-{{c}_{z2}} \right)\cos \theta \right]-2{{m}_{r}}{{y}_{\text{A}}}\cos {{\theta }^{^{^{_{^{{}}}}}}} \right. \\ & \left. -\frac{3}{20}\left( T_{a2}^{2}\left( -{{a}_{y2}}\sin \theta +{{a}_{z2}}\cos \theta \right)+\left( T_{a1}^{2}+T_{a2}^{2} \right){{k}_{r}}{{y}_{\text{A}}}\cos \theta \right) \right\} \\ & \Delta {{r}_{r}}=\Delta {{r}_{1}}-\Delta {{r}_{2}}=\left( {{d}_{y2}}-{{d}_{y1}} \right)\sin \theta +\left( {{d}_{z1}}-{{d}_{z2}}-2{{n}_{r}}{{y}_{\text{A}}} \right)\cos \theta \\ \end{align} \right\}$ | (30) |
分析式(30)可知,多波段SAR图像的方位向配准误差与对应波段合成孔径时间内的残余平动误差的线性项系数之差、杠杆臂的长度成正比,残余运动误差的3次项引起的多波段图像方位向配准误差受到合成孔径时间的平方的加权。低频波段SAR系统波束角比较宽,合成孔径时间长,残余运动误差的3次项引起的图像定位误差不可忽略。距离向配准误差主要由不同波段在对应合成孔径时间内残余运动误差的常数项之差引起。
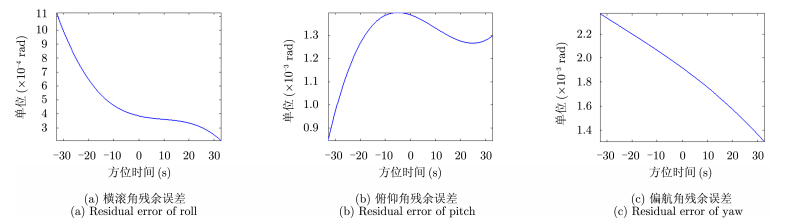
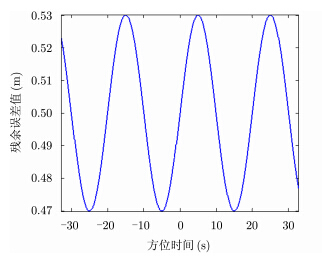
4.3 仿真验证与分析以表 1中的参数进行仿真实验,基线长2 m,两部天线的杠杆臂长度都为1 m。其中,X波段杠杆臂矢量沿斜轴负方向,P波段杠杆臂矢量沿斜轴正方向。仿真中在成像区域内设置5个点目标,这些点在图 1所示坐标系中的位置如表 1所示。仿真中加入的残余姿态误差如图 4所示,水平方向加入的残余平动误差如图 5所示,仿真实验与理论计算的配准误差结果如图 6所示。
| 表 1 仿真参数 Tab.1 Simulation parameters |
|
图 4 残余姿态误差 Fig.4 Residualattitude error |
|
图 5 残余平动误差 Fig.5 Residual trajectory deviation |
|
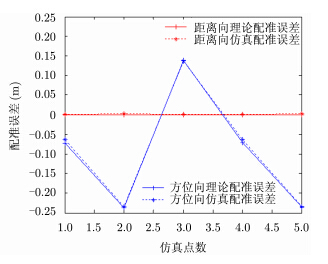
图 6 配准误差 Fig.6 Registration error |
由图 6可见,距离向和方位向仿真得到的配准误差与理论计算的配准误差都比较吻合。为了进一步定量验证本文的分析结果,对成像区域内每个点目标对应合成孔径时间内的残余运动误差进行多项式拟合。根据拟合的多项式系数,由式(30)计算得到两波段的配准误差,与仿真得到的配准误差比较结果如表 2所示。
| 表 2 理论与仿真配准误差结果比较结果 Tab.2 Results comparison of the theoretical and thesimulation registration error |
比较表 2中理论计算的配准误差和仿真结果的配准误差,二者误差都在${{10}^{-3}} \text{m}$量级,基本在量化误差范围内,表明了本文理论分析的正确性。由表 2可知,加入上述残余运动误差时,两波段成像场景中(±1000, 4000, 3000) m处的点目标方位向配准误差已接近-0.24 m。其中,-0.04 m配准误差来自不同波段对应合成孔径时间内残余平动误差的线性项,-0.19 m配准误差主要来自P波段残余平动误差的3次项,0.01 m配准误差来自残余姿态误差线性项。可见,两个波段的方位向配准误差大部分来源于低频波段SAR系统合成孔径时间内残余运动误差的3次项。两个波段LOS方向的常数项残余运动误差非常接近,所以距离向配准误差很小。
当不同波段对应合成孔径时间内的残余平动误差线性项系数相近,低频波段SAR系统残余平动误差的3次项系数比较小时,机载多波段SAR图像的配准误差比较小。残余姿态误差导致多波段SAR图像的配准误差与杠杆臂长度成正比。杠杆臂越短,机载多波段SAR图像的配准误差越小。
5 结论本文根据相关文献以及运动测量系统的实测数据建立了残余运动误差模型,分析了残余运动误差对SAR成像几何定位误差的影响,在此基础上定量地研究了残余运动与机载多波段SAR图像配准误差的关系,并利用仿真实验进行了验证。通过理论分析和仿真验证得到如下结论:机载多波段SAR图像的方位向配准误差与对应波段合成孔径时间内残余平动误差的线性项系数之差、杠杆臂的长度成正比,残余运动误差的3次项引起的多波段图像方位向配准误差受到合成孔径时间的平方的加权;距离向配准误差主要由不同波段在对应合成孔径时间内残余运动误差的常数项之差引起。因此,如果不同波段对应合成孔径时间内的残余平动误差线性项系数比较接近,低频波段SAR系统残余平动误差的3次项较小,杠杆臂较短,残余运动误差引起的多波段SAR图像配准误差比较小。
| [1] |
刘向君.多波段SAR目标检测与图像分类融合[D]. [硕士论文], 国防科学技术大学, 2005. Liu Xiang-jun.Decision fusion of multi-band SAR target detection and classification results[D].[Master dissertation], National University of Defense Technology, 2005. (  1) 1)
|
| [2] |
Chang Wen-ge,Li Xiang-yang, Li Yue-li, et al.. Airborne multi-frequency-band SAR system and its information processing[C]. IEEE International Conference on Information and Automation, Zhangjiajie, 2008: 1807-1811.
( 1) 1)
|
| [3] |
冯卫平. 多波段多极化SAR图像配准技术研究[D]. [硕士论文], 杭州电子科技大学, 2009. Feng Wei-ping.A Study on the techniques of the multifrequency and multipolarization SAR imageregistration[D]. [Master dissertation], Hangzhou Dianzi University, 2009. (  2) 2)
|
| [4] |
吴一戎. 多维度合成孔径雷达成像概念[J]. 雷达学报, 2013, 2(2): 135-142. Wu Yi-rong.Concept on multidimensional space joint-observation SAR[J]. Journal of Radars, 2013, 2(2): 135-142. (  1) 1)
|
| [5] |
Ruan Xiang-wei,Chen Xi, Wu Tao, et al. Performance experiment of classification using chinese airborne multi-band and multi-polar SAR data[C]. International Symposiumon Image Data Fusion, Tengchong, 2011: 1-4.
( 1) 1)
|
| [6] |
林岳松, 冯卫平, 陈华杰. 基于尺度预估的SAR图像相位相关配准算法[J]. 现代雷达, 2010, 32(7): 39-44. Lin Yue-song,Feng Wei-ping, and Chen Hua-jie. A FFT- based SAR image registration algorithm via priority estimation of scale distortion[J]. Modern Radar, 2010,32(7): 39-44. (  1) 1)
|
| [7] |
常玉林. 多波段SAR图像配准及融合算法研究[D]. [硕士论文], 国防科学技术大学, 2004. Chang Yu-lin. A research on the algorithms of registration and fusion for multi-spectral SAR images[D].[Master dissertation], National University of Defense Technology, 2004. (  1) 1)
|
| [8] |
宋明明, 韩春明, 廖静娟. X波段和全极化P波段SAR图像配准方法研究[J]. 测绘通报, 2013, (4): 8-11 . Song Ming-ming, Han Chun-ming, and Liao Jing-juan.Research on X band and fully polarimetric P band SAR image registration[J]. Bulletin of Surveying and Mapping, 2013, (4): 8-11. (  1) 1)
|
| [9] |
Peterson E H, Fotopoulos G, Schmitt A, et al.. Registration of multi-frequency SAR imagery using phase correlation methods[C]. IEEE Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 2011: 3708-3711.
( 1) 1)
|
| [10] |
Reigber A, Jager M, Fischer J, et al.. Performance of the L-and P-band subsystems of the F-SAR airborne SAR instrument[C]. The European Conference on Synthetic Aperature
Radar, Nuremberg, German, 2012: 286-289.
( 1) 1)
|
| [11] |
李焱磊. 机载差分干涉SAR运动补偿技术研究[D]. [博士论文], 中国科学院电子学研究所, 2013 . Li Yan-lei.Research on motion compensation in airborne differential synthetic aperturer adar interferometry[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2013. (  1) 1)
|
| [12] |
Reigber A. Correction of residual motion errors in airborne SAR interferometry[J]. Electronics Letters, 2001, 37(17): 1083-1084.
( 1) 1)
|
| [13] |
保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 196-198. Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technology[M]. Beijing: Publishing Houseof Electronics Industry, 2005: 196-198. (  1) 1)
|
| [14] |
Fornaro G, Franceschetti G, and Perna S. Motion compensation errors: effects on the accuracy of airborne SAR images[J]. IEEE Transactions on Aerospace Electronic Systems, 2005, 41(4): 1338-1352.
( 2) 2)
|
| [15] |
句赫. 机载合成孔径雷达运动补偿研究[D]. [硕士论文], 中国科学院电子学研究所, 2006. Ju He. Research on motion compensation of airborne SAR[D]. [Master dissertation], Institute of Electronics, Chinese Academy of Sciences, 2006. (  1) 1)
|
| [16] |
郭春梅. 基于运动参量的机载SAR运动补偿研究[D]. [博士论文], 中国科学院电子学研究所, 2008. Guo Chun-mei.Research on motion compensation based onmotion parameters for airborne SAR[D].[Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences,2008. (  1) 1)
|
| [17] |
Ni Chong, Wang Yan-fei, Xu Xiang-hui, et al.. SAR motion compensation based on the correction of residual attitude errors[J]. SCIENCE CHINA Physics, Mechanics & Astronomy, 2011, 54(10):1899-1905.
( 1) 1)
|
| [18] |
毛永飞. 机载双天线干涉SAR误差补偿与定标技术研究[D]. [博士论文], 中国科学院电子学研究所, 2012. Mao Yong-fei.Research on compensation and calibration for airborne dual-antenna interferometric SAR[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2012. (  1) 1)
|


