1 引言
在窄带多径环境下,由于多径干扰会对消期望信号,传统波束形成算法性能将急剧下降甚至失效[1]。为解决此问题,多径干扰波束形成算法得到广泛地研究,目前,根据对多径干扰的处理方式不同,可分为多径干扰抑制波束形成算法和多径信号接收波束形成算法。
多径干扰抑制波束形成算法主要是通过解相干处理或线性约束实现期望信号的有效接收。一类典型的解相干处理算法是空间平滑算法[2, 3, 4],该算法可以有效地实现解相干处理,但是牺牲了阵列的有效孔径,且稳健性较差。此外,学者还提出了如:多零陷约束算法[5]、时域加权主成分分析算法[6]以及结合最差性能约束、软约束和Duvall结构的稳健算法等[7, 8]。
多径信号接收波束形成算法[9, 10, 11, 12]对多径信号联合接收,目的是为充分利用多径信号信息。文献[11]首先利用变换矩阵去除阵列接收数据中非相关干扰信息,并估计多径信号的合成导向矢量,然后基于合成导向矢量和阵列协方差矩阵的特征结构进行波束形成,该算法有效实现了多径信号的接收,且具有较快的收敛速度,但需估计非相关干扰的信号来向。文献[12]通过在期望信号和多径干扰来向附近施加最差性能约束实现了多径信号的联合接收,且具有较好的稳健性,但该算法需估计多径干扰来向,且阵列输出性能易受多径信号初始相位差的影响。
本文首先分析多径环境下期望信号对消的原因:对应期望信号和多径干扰的阵列输出间的相位差始终在$\ {π}$附近变化。然后基于反对角单位阵构造新的数据协方差矩阵和导向矢量,利用最小方差无畸变准则进行波束输出,该算法可以有效地补偿期望信号和多径干扰对应的阵列输出间的相位差,并可通过选取合适的阵元个数获取更优的阵列输出性能。最后,仿真实验分析验证了算法的有效性。
2 信号模型和Capon波束形成器
考虑$P$个远场窄带平面波${s_i}(t)(i = 0,1, \cdots ,P - 1)$以角度${\theta _i}$入射到$M$阵元均匀直线阵。假定${s_0}(t)$是期望信号,其余$P - 1$个信号与${s_0}(t)$非相关,且${s_0}(t)$存在$Q$个多径干扰,其来波方向为${\widehat \theta _q}(q = 1,2, \cdots ,Q)$,每个多径干扰由期望信号经幅度衰减和相位延迟得到,即:
|
${\widehat s_q}(t) = {\rho _q}{{\rm{e}}^{ - {\rm{j}}{{\widehat \phi }_q}}}{s_0}(t)$
|
(1)
|
其中${\widehat s_q}(t)$表示第$q$个多径信号,${\rho _q}$表示第$q$个多径信号相对期望信号的幅度衰减因子,${\widehat \phi _q}$为多径传播引起的相位差。
假定阵元间距为$d$,波达方向为$\theta $的信号的导向矢量$a$$(\theta )$可表示为:
|
$a$$(\theta ) = {\left[ {\begin{array}{*{20}{c}}
1&{{{\rm{e}}^{ - {\rm{j}}2\pi \frac{d}{\lambda }\sin \theta }}}& \cdots &{{{\rm{e}}^{ - {\rm{j}}(M - 1)2\pi \frac{d}{\lambda }\sin \theta }}}
\end{array}} \right]^{\rm{T}}}$
|
(2)
|
其中$\lambda $为信号波长。$t$时刻阵列接收数据矢量为:
|
$x(t) = \left[ {{a}({\theta _0}) + \sum\limits_{q = 1}^Q {{a}({{\widehat \theta }_q}){\rho _q}{{\rm{e}}^{ - {\rm{j}}{{\widehat \phi }_q}}}} } \right]{s_0}(t) + \sum\limits_{i = 1}^{P - 1} {{a}({\theta _i})} {s_i}(t) + {n}(t)$
|
(3)
|
其中
n$(t)$为阵列接收噪声矢量。
阵列输出可表示为:
|
$y(t) = {{w}^{\rm{H}}}{x}(t)$
|
(4)
|
其中
w为复加权矢量。
传统Capon波束形成器[13]在满足阵列输出功率最小化的同时约束期望方向阵列响应为1,可表示为如式(5)优化问题:
|
$\left. \begin{array}{l}
\mathop {\min }\limits_{w} {{w}^{\rm{H}}}{Rw}\\
{\rm{s}}{\rm{.t}}{\rm{. }}{{w}^{\rm{H}}}{a}({\theta _0}) = 1
\end{array} \right\}$
|
(5)
|
其中
R是
M×M维协方差矩阵。实际应用中,
R用采样协方差矩阵代替
|
$\widehat {R} = \frac{1}{N}\sum\limits_{n = 1}^N {{x}(n)} {{x}^{\rm{H}}}(n)$
|
(6)
|
其中$N$为采样点数。利用拉格朗日乘子法,上述优化问题的解为:
|
${{w}_{{\rm{opt}}}} = \frac{{{{\widehat {R}}^{ - 1}}{a}({\theta _0})}}{{{{a}^{\rm{H}}}({\theta _0}){{\widehat {R}}^{ - 1}}{a}({\theta _0})}}{\rm{ = }}\mu {\widehat {R}^{ - 1}}{a}({\theta _0})$
|
(7)
|
其中
|
$\mu {\rm{ = }}\frac{1}{{{{a}^{\rm{H}}}({\theta _0}){{\widehat {R}}^{ - 1}}{a}({\theta _0})}}$
|
|
在理想条件下,传统Capon波束形成器能够有效地抑制非相关干扰。但当多径干扰存在时,多径干扰会引起期望信号对消,波束形成器性能将急剧下降,甚至失效。下面给出期望信号对消的具体原因。
3 多径环境下期望信号对消原因
假定$M = 2, P = 1, Q = 1$,期望信号为复指数信号,其离散形式为:
|
${s_0}(n) = A{{\rm{e}}^{{\rm{j}}2\rm{\pi} f{t_n}}} = A{{\rm{e}}^{{\rm{j}}{\phi _0}(n)}}$
|
(8)
|
其中$A$为期望信号幅度,${t_n}$为第$n$个采样点对应的采样时刻。则多径干扰可表示为:
|
${\widehat s_1}(n) = {\rho _1}{{\rm{e}}^{ - {\rm{j}}{{\widehat \phi }_1}}}{s_0}(n) = {\rho _1}A{{\rm{e}}^{{\rm{j}}({\phi _0}(n) - {{\widehat \phi }_1})}} = {\rho _1}A{{\rm{e}}^{{\rm{j}}{\phi _1}(n)}}$
|
(9)
|
期望信号和多径干扰信号的导向矢量${a}({\theta _0})$和${a}({\widehat \theta _1})$分别为:
|
${a}({\theta _0}) = {\left[ {\begin{array}{*{20}{c}}
1&{{{\rm{e}}^{ - {\rm{j}}2\rm{\pi} \frac{d}{\lambda }\sin {\theta _0}}}}
\end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}}
1&{{{\rm{e}}^{{\rm{j}}{\phi _{{\theta _0}}}}}}
\end{array}} \right]^{\rm{T}}}$
|
(10)
|
|
${a}({\widehat \theta _1}) = {\left[ {\begin{array}{*{20}{c}}
1&{{{\rm{e}}^{ - {\rm{j}}2\rm{\pi} \frac{d}{\lambda }\sin {{\widehat \theta }_1}}}}
\end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}}
1&{{{\rm{e}}^{{\rm{j}}{\phi _{{{\widehat \theta }_1}}}}}}
\end{array}} \right]^{\rm{T}}}$
|
(11)
|
忽略噪声项n(t)的影响,阵列接收数据矢量可表示为:
|
${x}(n) = A{\left[ {\begin{array}{*{20}{c}}
{{{\rm{e}}^{{\rm{j}}{\phi _0}(n)}} + {\rho _1}{{\rm{e}}^{{\rm{j}}{\phi _1}(n)}}}&{{{\rm{e}}^{{\rm{j}}({\phi _0}(n) + {\phi _{{\theta _0}}})}} + {\rho _1}{{\rm{e}}^{{\rm{j}}({\phi _1}(n) + {\phi _{{{\widehat \theta }_1}}})}}}
\end{array}} \right]^{\rm{T}}}$
|
(12)
|
根据式(6)和式(12)可得阵列接收数据协方差矩阵
|
${R} = {A^2}\left[ {\begin{array}{*{20}{c}}
{1 + \rho _1^2 + {\rho _1}{{\rm{e}}^{{\rm{j}}{{\widehat \phi }_1}}} + {\rho _1}{{\rm{e}}^{ - {\rm{j}}{{\widehat \phi }_1}}}}&{{{\rm{e}}^{ - {\rm{j}}{\phi _{{\theta _0}}}}} + \rho _1^2{{\rm{e}}^{ - {\rm{j}}{\phi _{{{\widehat \theta }_1}}}}} + {\rho _1}{{\rm{e}}^{{\rm{j}}({{\widehat \phi }_1} - {\phi _{{{\widehat \theta }_1}}})}} + {\rho _1}{{\rm{e}}^{ - {\rm{j}}({{\widehat \phi }_1} + {\phi _{{\theta _0}}})}}}\\
{{{\rm{e}}^{{\rm{j}}{\phi _{{\theta _0}}}}} + \rho _1^2{{\rm{e}}^{{\rm{j}}{\phi _{{{\widehat \theta }_1}}}}} + {\rho _1}{{\rm{e}}^{ - {\rm{j}}({{\widehat \phi }_1} - {\phi _{{{\widehat \theta }_1}}})}} + {\rho _1}{{\rm{e}}^{{\rm{j}}({{\widehat \phi }_1} + {\phi _{{\theta _0}}})}}}&{1 + \rho _1^2 + {\rho _1}{{\rm{e}}^{{\rm{j}}({{\widehat \phi }_1} + {\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}})}} + {\rho _1}{{\rm{e}}^{{\rm{j}}({\phi _{{{\widehat \theta }_1}}} - {{\widehat \phi }_1} - {\phi _{{\theta _0}}})}}}
\end{array}} \right]$
|
(13)
|
将式(10)和式(13)代入式(7)得最优加权矢量
|
${{w}_{{\rm{opt}}}} = \frac{{\mu {A^2}}}{{\left| {R} \right|}}\left[ \begin{array}{l}
\rho _1^2 - \rho _1^2{{\rm{e}}^{{\rm{j}}({\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}})}} - {\rho _1}{{\rm{e}}^{ - {\rm{j}}{{\widehat \phi }_1}}} + {\rho _1}{{\rm{e}}^{{\rm{j}}({\phi _{{{\widehat \theta }_1}}} - {{\widehat \phi }_1} - {\phi _{{\theta _0}}})}}\\
\rho _1^2{{\rm{e}}^{{\rm{j}}{\phi _{{\theta _0}}}}} - \rho _1^2{{\rm{e}}^{{\rm{j}}{\phi _{{{\widehat \theta }_1}}}}} + {\rho _1}{{\rm{e}}^{{\rm{j}}({\phi _{{\theta _0}}} - {{\widehat \phi }_1})}} + {\rho _1}{{\rm{e}}^{{\rm{j}}({\phi _{{{\widehat \theta }_1}}} - {{\widehat \phi }_1})}}
\end{array} \right]$
|
(14)
|
其中$\left| {R} \right|$为${R}$的行列式值。根据式(4),对应期望信号的阵列输出为:
|
${y_0}(n) = {w}_{{\rm{opt}}}^{\rm{H}}{a}({\theta _0}){s_0}(n) = \frac{{\mu {A^3}\rho _1^2{{\rm{e}}^{{\rm{j}}{\phi _0}(n)}}}}{{\left| {R} \right|}}\left[ {2 - {{\rm{e}}^{{\rm{j}}({\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}})}} - {{\rm{e}}^{{\rm{j}}({\phi _{{{\widehat \theta }_1}}} - {\phi _{{\theta _0}}})}}} \right]$
|
(15)
|
对应多径干扰的阵列输出为:
|
${y_1}(n) = {w}_{{\rm{opt}}}^{\rm{H}}{a}({\widehat \theta _1}){\widehat s_1}(n) = - \frac{{\mu {A^3}\rho _1^2{{\rm{e}}^{{\rm{j}}{\phi _0}(n)}}}}{{\left| {R} \right|}}\left[ {2 - {{\rm{e}}^{{\rm{j}}({\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}})}} - {{\rm{e}}^{{\rm{j}}({\phi _{{{\widehat \theta }_1}}} - {\phi _{{\theta _0}}})}}} \right] = {y_0}(n){{\rm{e}}^{ \pm {\rm{j}}\rm{\pi} }}$
|
(16)
|
对比式(15)和式(16)可知,${y_0}(n)$和${y_1}(n)$的幅值相等,相位差为$ \rm{\pi}$。阵列的输出为:
|
$y(n){\rm{ = }}{y_0}(n){\rm{ + }}{y_1}(n){\rm{ = }}0$
|
(17)
|
此时,期望信号被完全对消,因此Capon波束形成器的性能将急剧下降。上述分析是基于2个阵元,仅存在1个多径干扰条件下进行,随着阵元个数干扰数目的增加,我们发现阵列输出对应期望信号和多径干扰间的相位差仍在$\rm{\pi}$附近变化,由于推导过程较为复杂,本文在第5节给出了仿真验证。对窄带随机信号的理论推导见附录。
4 基于反对角单位阵的多径信号接收算法
基于上述分析,若能求取最优加权矢量使对应期望信号和多径干扰的阵列输出间的相位差不等于$ \rm{\pi}$,则可避免期望信号的完全对消,且随着相位差的逐渐减小,接收信号的幅值逐渐增大。
构造反对角单位阵
|
${J} = {\left[ {\begin{array}{*{20}{c}}
0& \cdots &0&1\\
\vdots & \ddots & \ddots &0\\
0& \ddots & \ddots & \vdots \\
1&0& \cdots &0
\end{array}} \right]_{M \times N}}$
|
(18)
|
使
|
$\widehat {x}(n) = {Jx}(n)$
|
(19)
|
易知${J} = {{J}^{\rm{T}}} = {{J}^{\rm{H}}} = {{J}^{ - 1}}$,因此新的阵列接收协方差矩阵为:
|
${\widehat {R}_J} = {\rm{E}}\left\{ {\widehat {x}(n){{\widehat {x}}^{\rm{H}}}(n)} \right\} = {\rm{E}}\left\{ {{Jx}(n){{x}^{\rm{H}}}(n){J}} \right\} = {JRJ}$
|
(20)
|
式(2)左侧乘以J可得新的阵列导向矢量为:
|
$\begin{array}{l}
{{a}_J}(\theta ) = {Ja}(\theta ) = {{\rm{e}}^{ - {\rm{j}}(M - 1)2\pi \frac{d}{\lambda }\sin \theta }}\left[ {1,{{\rm{e}}^{{\rm{j}}2\rm {\pi} \frac{d}{\lambda }\sin \theta }}, \cdots ,} \right.\\
{\left. {{{\rm{e}}^{{\rm{j}}(M - 1)2\rm {\pi} \frac{d}{\lambda }\sin \theta }}} \right]^{\rm{T}}} = {{\rm{e}}^{ - {\rm{j}}(M - 1)2\pi \frac{d}{\lambda }\sin \theta }}{{a}^ * }(\theta )
\end{array}$
|
(21)
|
由式(21)可知,${{a}_J}(\theta )$和${{a}^ * }(\theta )$间仅存在一个相位差,因此可认为${{a}_J}(\theta )$与${{a}^ * }(\theta )$等价。将式(20)和式(21)代入式(7)可得最优加权矢量为:
|
$\begin{array}{l}
{{w}_{{\rm{opt\_}}J}} = \frac{{\widehat {R}_J^{ - 1}{{a}_J}({\theta _0})}}{{{a}_J^{\rm{H}}({\theta _0})\widehat {R}_J^{ - 1}{{a}_J}({\theta _0})}} = \frac{{{J}{{R}^{ - 1}}{a}({\theta _0})}}{{{{a}^{\rm{H}}}({\theta _0}){{R}^{ - 1}}{a}({\theta _0})}}\\
= {J}{{w}_{{\rm{opt}}}}
\end{array}$
|
(22)
|
为使输出波束的波峰和零陷与原输入信号的方向对应,可以选择如下两种方式进行波束形成:
|
$\left| {{P_{{\rm{out}}}}(\theta )} \right| = \left| {{w}_{{\rm{opt\_}}J}^{\rm{H}}{{a}_J}(\theta )} \right|$
|
(23)
|
|
$\qquad \qquad \qquad \, \left| {{P_{{\rm{out}}}}(\theta )} \right| = \left| {{w}_{{\rm{opt\_}}J}^{\rm{T}}{a}_J^{\rm{*}}(\theta )} \right| = \left| {{w}_{{\rm{opt\_}}J}^{\rm{T}}{a}(\theta )} \right|$
|
(24)
|
其中$\left| {{P_{{\rm{out}}}}(\theta )} \right|$为$\theta $方向输出波束的模值。若按式(23)进行波束形成,阵列输出为:
|
${y_{{\rm{out}}}}(n) = {w}_{{\rm{opt\_}}J}^{\rm{H}}\widehat {x}(n){\rm{ = }}{w}_{{\rm{opt}}}^{\rm{H}}{{J}^{\rm{H}}}{Jx}(n) = {w}_{{\rm{opt}}}^{\rm{H}}{x}(n)$
|
(25)
|
此时,阵列输出与传统Capon波束形成器输出相同,期望信号将被完全对消。根据式(24),可得
|
${y_{{\rm{out}}}}(n) = {w}_{{\rm{opt\_}}J}^{\rm{T}}{x}(n){\rm{ = }}{w}_{{\rm{opt}}}^{\rm{T}}{Jx}(n)$
|
(26)
|
将${{x}_0}(n) = {a}({\theta _0}){s_0}(n)$和${{x}_1}(n) = {a}({\widehat \theta _1}){\widehat s_1}(n)$代入式(26)可得对应期望信号的多径干扰的阵列输出分别为:
|
$\begin{array}{l}
{\widehat y_0}(n) = {w}_{{\rm{opt}}}^{\rm{T}}{J}{{x}_0}(n)\\
\qquad \; \; = \frac{{\mu {A^3}\rho _1^2{{\rm{e}}^{{\rm{j}}({\phi _0}(n) - {\phi _{{{\widehat \theta }_1}}} \pm \pi )}}}}{{\left| R \right|}}{({{\rm{e}}^{{\rm{j}}{\phi _{{\theta _0}}}}} - {{\rm{e}}^{{\rm{j}}{\phi _{{{\widehat \theta }_1}}}}})^2}
\end{array}$
|
(27)
|
|
$\quad \, \begin{array}{l}
{\widehat y_1}(n) = {w}_{{\rm{opt}}}^{\rm{T}}{J}{{x}_1}(n)\\
\qquad \; \, \, = \frac{{\mu {A^3}\rho _1^2{{\rm{e}}^{{\rm{j}}(2{\phi _1}(n) - {\phi _0}(n) - {\phi _{{\theta _0}}})}}}}{{\left| {\bf{R}} \right|}}{({{\rm{e}}^{{\rm{j}}{\phi _{{\theta _0}}}}} - {{\rm{e}}^{{\rm{j}}{\phi _{{{\widehat \theta }_1}}}}})^2}
\end{array}$
|
(28)
|
对比式(27)和式(28)可得${\widehat y_0}(n)$和${\widehat y_1}(n)$的相位差为:
|
$\Delta \phi = 2{\widehat \phi _1} + {\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}} \pi $
|
(29)
|
与传统Capon算法对比,上述算法在对应期望信号和多径干扰的阵列输出间引入相位差$\Delta \widehat \phi = 2{\widehat \phi _1} + {\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}}, \Delta \widehat \phi $与$2k\pi , k \in Z$的差值越大,阵列输出性能越好。上述分析基于两个阵元和一个多径干扰,其中${\widehat \phi _1}$为多径干扰和期望信号间的初始相位差,当多径干扰数目增加时,${\widehat \phi _1}$将随着变化,而${\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}}$由多径信号入射到阵列的角度及阵列元个数决定,因此,$\Delta \widehat \phi $随着阵元个数和多径干扰数目的变化而变化,将$\Delta \widehat \phi $重新表述为:
|
$\Delta \widehat \phi = \Delta {\widehat \phi _p} + \Delta {\widehat \phi _\theta }$
|
(30)
|
其中$\Delta {\widehat \phi _p}$表示路径传播引起的相位差,当入射信号的传播路径固定时,$\Delta {\widehat \phi _p}$为一固定值,$\Delta {\widehat \phi _\theta }$表示阵列变化引起的相位差。传统多径信号接收算法的阵列输出主要由$\Delta {\widehat \phi _p}$决定,当$\Delta {\widehat \phi _p}$接近$2k\pi ,k \in Z$时,阵列输出性能将急剧下降。但是,本文算法中$\Delta {\widehat \phi _\theta }$随着阵列信息的变化而变化,实际应用中,可以调整选取的阵元数目以获取相对传统多径信号接收算法较优的阵列输出性能。基于上述分析,基于反对角单位阵的多径信号接收算法可表示为如下优化问题:
|
$\left. \begin{array}{l}
\mathop {\min }\limits_{w} {{w}^{\rm{H}}}{\widehat {R}_J}{w}\\
{\rm{s}}{\rm{.t}}{\rm{. }}{{w}^{\rm{H}}}{{a}^ * }({\theta _0}) = 1
\end{array} \right\}$
|
(31)
|
并基于式(26)求取阵列输出。
5 仿真实验
实验1 阵列输出性能随阵元个数变化性能分析
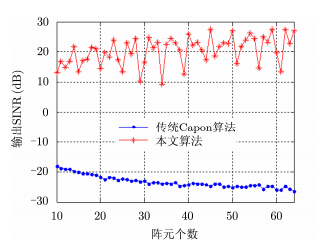
考虑一均匀直线阵,期望信号来向为15º,信噪声比(SNR)为10 dB。4个非相关干扰分别以角度-20º,30º,-55º和60º入射到阵列,干扰与噪声比(INR)为30 dB。两个多径干扰相对期望信号的幅度衰减因子${\rho _1}{\rm{ = }}{\rho _2}{\rm{ = }}0.5$,相位延迟在$[0,2\rm \pi ]$内随机产生,来向分别为-35º和45º。以第1个阵元为参考阵元,阵元间距为期望信号最高频率对应波长的一半,快拍数为512。每次试验均做200次蒙特卡罗试验求平均值。
图 1给出了阵元个数由10变化到64时,传统Capon算法和本文算法输出信号与干扰噪声比(SINR)的变化曲线。由图 1可知,本文算法的输出SINR远大于传统Capon算法,且随着阵元个数的增加在20 dB上下波动,与文中分析的阵元个数对阵列输出性能的影响一致。其中SINR由式(32)给出
|
${\rm{SIN}}{{R}_{{\rm{output}}}} = \frac{{{w}_{{\rm{opt\_}}J}^{\rm{T}}{{R}_{{\rm{s + ci}}}}{w}_{{\rm{opt\_}}J}^{\rm{*}}}}{{{w}_{{\rm{opt\_}}J}^{\rm{T}}{{R}_{{\rm{ui + n}}}}{w}_{{\rm{opt\_}}J}^{\rm{*}}}}$
|
(32)
|
其中${{R}_{{\rm{s + ci}}}}$表示期望信号和多径干扰对应的阵列接收数据协方差,${{R}_{{\rm{ui + n}}}}$为非相关干扰和噪声对应的阵列接收数据协方差。
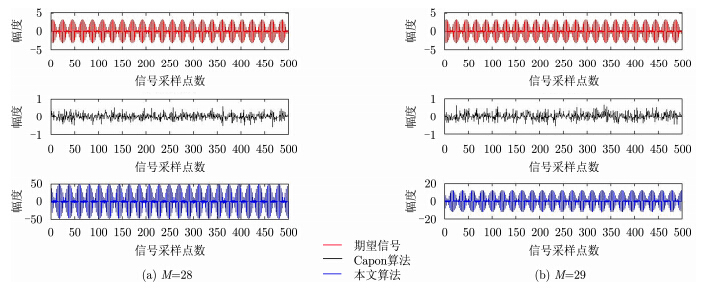
图 2(a)和图 2(b)分别给出了阵元个数分别为28和29时,传统Capon算法和本文算法输出信号实部与期望信号的对比图。对比图 1和图 2,当阵元个数为29时,阵列输出性能和输出信号的实部值均低于阵元个数为28时,但是输出信号实部值均大于期望信号,而传统Capon算法无法输出有效的信号。由图 1和图 2可知,阵列输出性能变化趋势随着阵元个数的变化存在不规律的周期性,因此在实际应用中,可在满阵元个数的基础上,减少进行波束形成的阵元个数,以对比获取较优的阵列输出性能。
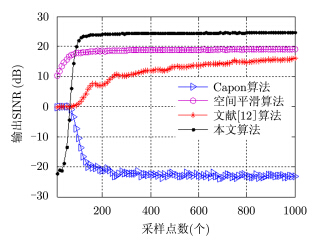
实验 2 阵列输出SINR随采样点数变化性能分析
设定阵元个数为28,改变采样点数由10到1000,其余仿真条件同实验1。图 3给出了不同采样点数下本文算法、文献[12]算法、空间平滑算法和传统Capon算法的输出SINR变化曲线。由图 3可知,本文算法的输出SINR随采样点数的增加较快达到收敛值,收敛速度大于文献[12]算法和传统Capon算法,但是略慢于空间平滑算法。
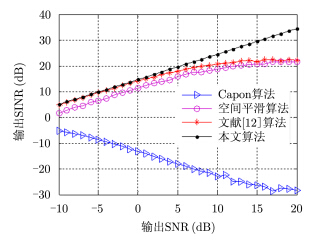
实验 3 输出SINR随输入SNR的变化性能分析
设定阵元个数为28,改变输入SNR由-10 dB到20 dB,其余仿真条件同实验1。图 4给出了不同输入SNR条件下本文算法、文献[12]算法、空间平滑算法和传统Capon算法的输出SINR变化曲线。由图 4可知,本文算法输出SINR优于文献[12]算法、空间平滑算法和传统Capon算法,且差值随着输入SNR的增加而增大。
实验 4 对应期望信号和多径干扰的阵列输出间的相位差变化分析
表 1给出了不同阵元个数和入射角度下本文算法、文献[12]算法和传统Capon算法对应期望信号和多径干扰的阵列输出间的相位差,其中初始相位差为多径传播路径延迟引起。由表 1中数据可知,传统Capon算法的输出相位差始终在$ \rm \pi $附近变化,进一步验证了多径环境下传统Capon算法中期望信号对消的原因;文献[12]算法的输出相位差与初始相位差一致,阵列输出性能将多径传播引起的相位差决定,当初始相位差接近$ \rm \pi $时,阵列输出性能将急剧下降;本文算法的输出相位差不仅受初始相位差影响,而且受阵元个数和多径信号入射角度的影响,因此,当入射到阵列的多径信号确定时,可以通过调整选取的阵元的个数修正阵列输出间的相位差,从而提高阵列输出性能。
表 1(Tab.1)
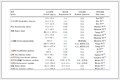
表 1 对应期望信号和多径干扰的阵列输出间的相位差Tab.1 The phase difference of the array output corresponding to the SOI and multipath interferences
| DOAs | 阵元个数 | | 24 | 25 | | 5º | 25º | -10º | 15º | 5º | 25º | -10º | 15º | | 初始相位差 | 2.6928 | -0.5984 | 2.6928 | -0.5984 | 2.6928 | -0.5984 | 2.6928 | -0.5984 | | 传统Capon算法 | -3.1408 | 3.1410 | 3.1406 | -3.1408 | -3.1411 | 3.1410 | 3.1414 | -3.1411 | | 文献[12]算法 | 2.6928 | -0.5984 | 2.6928 | -0.5984 | 2.6928 | -0.5984 | 2.6928 | -0.5984 | | 本文算法 | 0.1956 | -0.1022 | 0.5897 | 0.2886 | 1.1996 | 0.9012 | 1.8828 | 1.5829 |
|
表 1 对应期望信号和多径干扰的阵列输出间的相位差
Tab.1 The phase difference of the array output corresponding to the SOI and multipath interferences |
6 结束语
本文针对多径环境下传统Capon波束形成算法中期望信号对消的问题,分析了期望信号对消的原因,并提出一种基于反对角单位阵的多径信号接收算法。理论分析和仿真实验表明,该算法能够有效地避免期望信号的对消,且能够获得优于传统多径信号接收算法的输出性能。
附录
窄带随机信号的复指数形式可表示为:
|
$s(t) = M(t){{\rm{e}}^{{\rm{j}}{w_0}t}}$
|
(A-1)
|
其中$M(t)$为$s(t)$的复包络,${{\rm{e}}^{{\rm{j}}{w_0}t}}$为复载频。其多径形式可表示为:
|
$s(t - \tau ) = \rho M(t - \tau ){{\rm{e}}^{{\rm{j}}{w_0}(t - \tau )}}$
|
(A-2)
|
结合式(10)和式(11)可得阵列接收数据为:
|
${x}(t) = {\left[ {\begin{array}{*{20}{c}}
{M(t){{\rm{e}}^{{\rm{j}}{w_0}(t)}} + \rho M(t - \tau ){{\rm{e}}^{{\rm{j}}{w_0}(t - \tau )}}}&{M(t){{\rm{e}}^{{\rm{j}}{w_0}(t)}}{{\rm{e}}^{{\rm{j}}{\phi _{{\theta _0}}}}} + \rho M(t - \tau ){{\rm{e}}^{{\rm{j}}{w_0}(t - \tau )}}{{\rm{e}}^{{\rm{j}}{\phi _{_{{{\widehat \theta }_1}}}}}}}
\end{array}} \right]^{\rm{T}}}$
|
(A-3)
|
则$t$时刻阵列接收数据协方差矩阵为:
|
$\begin{array}{c}
{R}(t) = \left[ {\begin{array}{*{20}{c}}
{{M^2}(t) + {\rho ^2}{M^2}(t - \tau ) + \rho M(t){M^*}(t - \tau ){{\rm{e}}^{{\rm{j}}{w_0}\tau }} + \rho M(t - \tau ){M^*}(t){{\rm{e}}^{ - {\rm{j}}{w_0}\tau }}}\\
{{M^2}(t){{\rm{e}}^{ - {\rm{j}}{\phi _{{\theta _0}}}}} + {\rho ^2}{M^2}(t - \tau ){{\rm{e}}^{ - {\rm{j}}{\phi _{{{\widehat \theta }_1}}}}} + \rho M(t){M^*}(t - \tau ){{\rm{e}}^{{\rm{j}}({w_0}\tau - {\phi _{{{\widehat \theta }_1}}})}} + \rho M(t - \tau ){M^*}(t){{\rm{e}}^{ - {\rm{j}}({w_0}\tau + {\phi _{{\theta _0}}})}}}
\end{array}} \right.\\
\left. {\begin{array}{*{20}{c}}
{{M^2}(t) + {\rho ^2}{M^2}(t - \tau ) + \rho M(t){M^*}(t - \tau ){{\rm{e}}^{{\rm{j}}({w_0}\tau + {\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}})}} + \rho M(t - \tau ){M^*}(t){{\rm{e}}^{ - {\rm{j}}({w_0}\tau + {\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}})}}}\\
{{M^2}(t){{\rm{e}}^{{\rm{j}}{\phi _{{\theta _0}}}}} + {\rho ^2}{M^2}(t - \tau ){{\rm{e}}^{{\rm{j}}{\phi _{{{\widehat \theta }_1}}}}} + \rho M(t - \tau ){M^*}(t){{\rm{e}}^{{\rm{j}}({w_0}\tau - {\phi _{{{\widehat \theta }_1}}})}} + \rho M(t){M^*}(t - \tau ){{\rm{e}}^{ - {\rm{j}}({w_0}\tau + {\phi _{{\theta _0}}})}}}
\end{array}} \right]
\end{array}$
|
(A-4)
|
记
|
$\left. \begin{array}{l}
{\rm{E}}\left[ {{M^2}(t)} \right] = {\rm{E}}\left[ {{M^2}(t - \tau )} \right]{\rm{ = }}a\\
{\rm{E}}\left[ {M(t){M^*}(t - \tau )} \right] = {\rm{E}}\left[ {M(t - \tau ){M^*}(t)} \right]{\rm{ = }}b
\end{array} \right\}$
|
(A-5)
|
故
|
$\begin{array}{c}
\widehat {R} = {\rm{E}}\left[ {{R}(t)} \right]\\
{\rm{ = }}\left[ {\begin{array}{*{20}{c}}
{a + {\rho ^2}a + \rho b{{\rm{e}}^{{\rm{j}}{w_0}\tau }} + \rho b{{\rm{e}}^{ - {\rm{j}}{w_0}\tau }}}&{a + {\rho ^2}a + \rho b{{\rm{e}}^{{\rm{j}}({w_0}\tau + {\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}})}} + \rho b{{\rm{e}}^{ - {\rm{j}}({w_0}\tau + {\phi _{{\theta _0}}} - {\phi _{{{\widehat \theta }_1}}})}}}\\
{a{{\rm{e}}^{ - {\rm{j}}{\phi _{{\theta _0}}}}} + {\rho ^2}a{{\rm{e}}^{ - {\rm{j}}{\phi _{{{\widehat \theta }_1}}}}} + \rho b{{\rm{e}}^{{\rm{j}}({w_0}\tau - {\phi _{{{\widehat \theta }_1}}})}} + \rho b{{\rm{e}}^{ - {\rm{j}}({w_0}\tau + {\phi _{{\theta _0}}})}}}&{a{{\rm{e}}^{{\rm{j}}{\phi _{{\theta _0}}}}} + {\rho ^2}a{{\rm{e}}^{{\rm{j}}{\phi _{{{\widehat \theta }_1}}}}} + \rho b{{\rm{e}}^{{\rm{j}}({w_0}\tau - {\phi _{{{\widehat \theta }_1}}})}} + \rho b{{\rm{e}}^{ - {\rm{j}}({w_0}\tau + {\phi _{{\theta _0}}})}}}
\end{array}} \right]
\end{array}$
|
|
(A-6)
|
对比式(13)和式(A-6)可知,式(A-6)各项的常数和复指数项与式(13)具有相同的形式,又因为最优权矢量仅与$R$和期望信号导向矢量有关,故阵列输出对应期望信号和多径干扰间的相位差为$ \pm \pi $。
 1)
1)
 1)
1)
 1)
1)
 1)
1)
 1)
1)
 1)
1)
 1)
1)
 1)
1)
 1)
1)
 1)
1)
 2)
2)
 8)
8)
 1)
1)


